Powszechny jest pogląd, że pręt rozciągany nie może utracić stateczności. Tymczasem pręt rozciągany, wykonany z dowolnego materiału, również liniowo-sprężystego – traci stateczność, co pokazano na rys.1. Można to wykazać przy analizie dużych odkształceń pręta, przy czym nie jest to utrata stateczności w sensie Eulera.
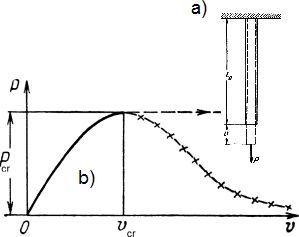Rys.1. Stateczność peta rozciąganego: a) schemat pręta i oznaczenia, b) – ścieżka równowagi; Pcr – obciążenie krytyczne [1]
Odksztalcenie liniowe definuje się klasycznie (przy malych oskształceniach $\varepsilon$ w postaci:
| $ \varepsilon= \dfrac{\Delta l}{l_0}$, | (1) |
gdzie: $l_0$ – początkowa długość włókna (rys.1a), $\Delta l=l-l_0$ – bezwzględne wydłużenie; $l$ – długosdc włókna po wydłuzeniu. Na rys. 1a $v=\Delta l$).
Definicja (1) nie wyjaśnia zjawisk zachodzących podczas procesu obciążania badanych próbek, gdzie długość pręta narasta od $l_0$ do $l$ w sposób ciągły i jest sumą przyrostów odkształcenia w poszczególnych krokach (ocinkach czasu) $\varepsilon=\sum \Delta \varepsilon$. W zapisie ciągłym mamy
| $ d\varepsilon = \dfrac {dz}{z}$, $\varepsilon= \int \limits _{l_0}^l \dfrac {1}{z} dz=ln \dfrac {l}{l_0}=ln \left( \dfrac{\Delta l}{l_0}\right )$ |
(2) |
gdzie: z- jest zmienną długością pręta a różniczka dz – przyrostem tej zmiennej w danej chwili. Wyrazenie na duże odkształcenie (2) (odkształcenie logarytmiczne) różni się od (1) tym bardziej im większy jest stosunek $\dfrac{\Delta l}{l_0}$. Z rozwinięcia w szereg Taylora mamy bowiem:
| $ln \dfrac{l}{l_0}=ln \left(1+ \dfrac{\Delta l}{l_0}\right ) \approx \dfrac{\Delta l}{l_0}-1 \dfrac {1}{2}(\dfrac{\Delta l})^2 +…-$ | (3) |
Miary małych deformacji Cauchy (1) i dużych deformacji Hencky (2) nie są jedynymi. Inne definicje są następujace:
| Almansi $ \varepsilon = \dfrac{1}{2} \left( 1- \dfrac{1}{\lambda^2}\right)$ | (4) |
| Koerber- Schaiger $ \varepsilon = 1- \dfrac{1}{\lambda}$ | (5) |
| Kun $ \varepsilon = \dfrac{1}{3} \left( \lambda^2- \dfrac{1}{\lambda}\right)$ | (6) |
| Green $ \varepsilon = \dfrac{1}{2} ( \lambda^2- 1)$ | (7) |
gdzie:
| $\lambda=\dfrac{l}{l_0}=\dfrac{l_0 + \Delta l}{l_0}$ | (8) |
Na rys.2 porównano krzywe dla etgo samego materiału, ale inncyh definicji odkształceń. Różnice są duże. Stąd spostrzeżenie Reissnera, który stwierdził, ze za miaręd efomacji można przyjąc dowolną bezwymaiarową funkcję $\lambda$ (8), jeśli tylko dla $\lambda \to 1$ dąży ona do miary Cauchy (1).
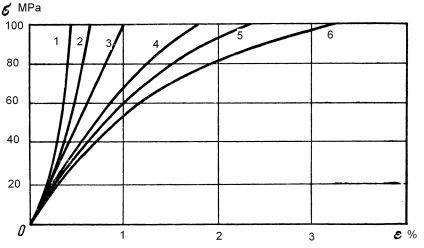Rys.2. Krzywe odksztalceń, uzyskane dla tych samych pomiarów, ale innych definicji odkształcenia: 1- Almansi, 2- Koerber- Schaiger , 3 -Hencky, 4-Couchy, 5-Kun, 6-Green [1]
Równanie krzywej utraty stateczności preta rozciąganego, zobrazowanej na rys.1. uzyskamy z analizy prawa Hooka w odkształceniach logarytmicznych. Klasyczne prawo Hooka zapiszmwy w postaci:
| $\sigma=E\varepsilon$ | (9) |
gdzie E- moduł Younga, $\varepsilon$ – odkształcenie logarytmiczne (2), $\sigma= \dfrac{P}{A}$ jest naprężeniem w przekroju pręta o powierzchni A. Oczywiście w stanie dużych odkształceń za pole przekroju $A$ weźmiemy rzeczywiste pole mniejsze od pola początkowego $A_0$:
| $A=A_0 \dfrac{l_0}{l}$ | (10) |
gdzie l – rzeczywista długość pręta w stosownym momencie rozciągania. Rozpatrzmy nieskończenie mały przedział tego procesu, podczas którego siła $P$ wzrośnie o $dP$, a naprężenie o $d \sigma$:
| $d \sigma= \dfrac{AdP-PdA}{A^2}$, | (11) |
gdzie z (10) mamy:
| $d A=- \dfrac{A_0 \cdot l_0)}{l^2}dl$, | (12) |
skad (11) przyjmuje postać:
| $d \sigma=\dfrac{dP+\dfrac{P}{l}dl}{A-) \dfrac{l_0}{l}}$, | (13) |
Z drugiej strony z (9) mamy przyrost naprężenia
| $d \sigma=E d\varepsilon=E \dfrac{dl}{l}$, | (14) |
Z porównania (13) i (14) otrzymujemy podstawowe równanie różniczkowe problemu:
| $\dfrac {dP}{dt}+\dfrac{P}{l}-\dfrac{EA_0 l_0}{l^2}$, | (15) |
Rozwiązanie równania (15) dla warunku początkowego $l=l_0$ dla $P=0$ ma postać
| $P=\dfrac{EA_0l_0}{l} ln\dfrac{l}{l_0}$, | (16) |
które po przekształceniu można zapisaćw postaci:
| $P=\dfrac{EA_0l_0}{1+\dfrac{v}{l_0}} ln\left(1+\dfrac{v}{l_0} \right) $, | (17) |
Wykres (17) przedstawiono na rys.1.
Podczas badań ze sterowaniem siłą, zadaje się wzrost siły z określoną prędkością. Po osiągnieciu wartości siły $ P_cr $ dalszy jej wzrost jest już niemożliwy – długość pręta rożnie bez przyrastania siły. To znaczy, że opadająca gałąź ścieżki równowagi, poprzekreślana na rys.1 – nie jest osiągana – przedstawia stany niestateczne. Wartość siły przy której nastąpi krytyczny stan otrzymujemy z warunku $\dfrac {dP}{dv}=0$, czyli:
| $P_{cr}=\dfrac{EA_0}{e}$, | (18) |
gdzie e- jest podstawą logarytmu naturalnego. Obciążeniu (18) odpowiada wydłużenie
| $v_{cr}=l_0(e-1) \approx 1,72 l_0$, | (19) |
po osiągnieciu którego przemieszczenia nieograniczenie wzrastają.
Obciążenie (18) nazywa się obciążeniem krytycznym pręta rozciąganego, a (19) krytycznym wydłużeniem.
Podobne wyniki uzyska się dla materiału dowolnie nieliniowo sprężystego, lub ciała plastycznego (współczynnik Poissona równy 0,5), a także dla doświadczenia ze sterowaniem przemieszczeniem.
W doświadczeniu ze sterowaniem przemieszczeniem mamy obciążenie krytyczne
| $P_{cr}=\dfrac{E(A_0-\Delta A_0}{e}$, | (20) |
przed osiągnięciu którego obciążenie będzie się zmniejszało i $P_{cr}$ nigdy nie będzie osiągnięte.
Opisane zjawiska potwierdzają badania eksperymentalne, które jednak często tłumaczone są mechanizmami plastycznych odkształceń struktury materiału, bo prawdopodobnie eksperymentatorzy nie znają analiz przedstawionych w niniejszym artykule za pracą [1].
Literatura
- Panovko J., G., Gubanova, I. I. (1967), Ustojčivost i kolebnija uprugich system. Sovremennyje koncepcii, paradoksy i ošibki (4th ed.), Nauka, Moskva
________________________________
