Analiza śrubowych połączeń doczołowych i innych jest prowadzona zgodnie z [1] z zastosowaniem zastępczych króćców teowych (T-króćców) oraz kołowych lub niekołowych mechanizmów zniszczenia blach. W śrubowym połączeniu czołowym rygla ze słupem, pokazanym na rys. 1a) analizuje się mechanizmy zniszczenia T-króćca (rys. 1b,c). Mechanizmy zniszczenia mogą być kołowe (rys.1h) , niekołowe (rys. 1i) lub mieszane (rys.1j). Mechanizmy zniszczenia prowadzą do siatki linii załomów plastycznych, których analiza jest przedmiotem teorii nośności granicznej (plastycznej) płyt.
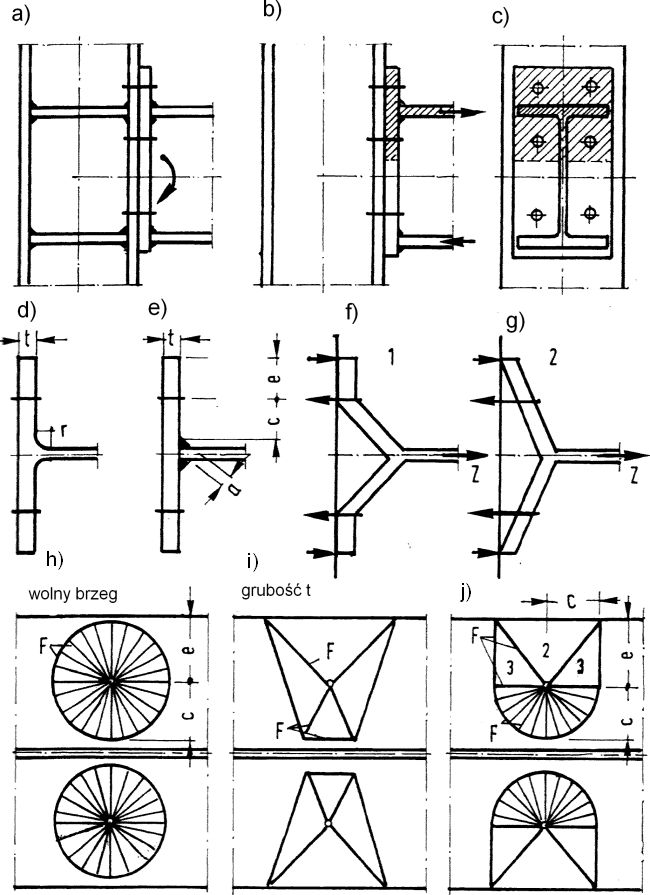
Rys. 1. Połączenie czołowe rygla ze słupem, F-linie załomów: a) schemat, b, c) zastępczy T-króciec, d) T-króciec kształtownika walcowanego, e) T-króciec blachownicy, f) mechanizm zniszczenia podstawowy (1), g) mechanizm zniszczenia z efektem dźwigni (2), h) mechanizm zniszczenia kołowy, i) mechanizm zniszczenia niekołowy, j) mechanizm zniszczenia kombinowany [2], str. 265
Teoria linii załomów plastycznych
Wprowadzenie
Teoria linii załomów stanowi podejście kinematyczne do szacowania nośności granicznej – plastycznej płyt zarówno izotropowych (np stalowych) jak i ortotropowych (np. żelbetowych) [3],149 . Ukształtowała się .już w 1949 roku z syntezy linii rys , obserwowanych w płytach żelbetowych znacznie wcześniej od sformułowania twierdzeń ekstremalnych nośności granicznej [4] , [5] .
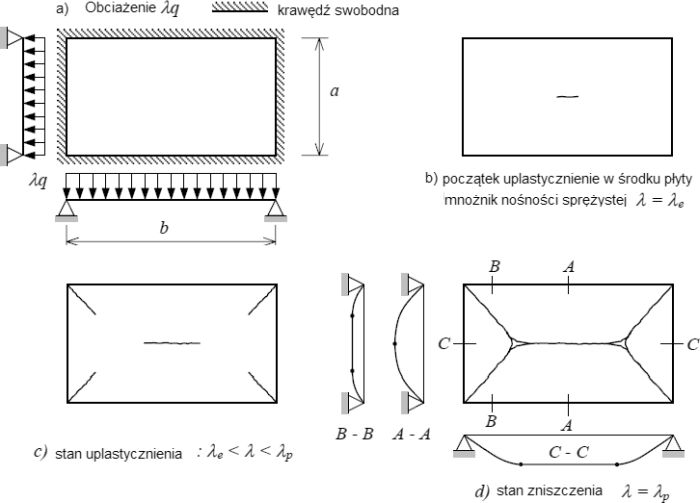
Rys.2. Proces zniszczenia płyty: a) schemat i obciążenie płyty swobodnie podpartej na obwodzie, b) nośność sprężysta$\lambda_e$, c) pośredni stan uplastycznienia, d)nośność plastyczna (graniczna) [6]
Rys. 2a przedstawia prostokątną płytę wykonaną z materiału idealnie-plastycznego o bokach axb, podpartą przegubowo na obwodzie i obciążoną równomiernie $\lambda q$. Wartość $q$ jest wartością stała, a $\lambda$ jest mnożnikiem obciążenia, który jest zmieniany od wartości zero( tuż przed obciążeniem) do wartości $\lambda_p$ , to jest do nośności granicznej płyty.. W pierwszym etapie obciążenia płyta zachowuje się całkowicie sprężyście, aż dochodzi do wartości $\lambda_e$, w której w 1-nym punkcie płyty następuje uplastycznienie (w przedmiotowej płycie w jej środku) . Ta wartość obciążenie nazywa się nośności sprężystą. W kolejnym etapie dla mnożnika $\lambda$ z przedziału $\lambda_e < \lambda < \lambda _p$ w płycie pojawiają się linie uplastycznienia, nazywane liniami załomów plastycznych. Przy obciążeniu $\ lambda_p$ utworzone linie uplastycznienia są tak rozległe, że pod obciążeniem następuje uruchomienie mechanizmu plastycznego. Taki stan nazywamy stanem granicznym lub plastycznym. Wytworzone odkształcenia plastyczne są trwałe i nie znikają po odciążeniu.
Po osiągnieciu wartości $\lambda_p$, obciążenia nie zwiększają się już i bez dalszego zwiększania obciążenia, nieograniczone są przemieszczenia płatów płyty wyciętych liniami załomów, tylko ze względu na rosnące odkształcenia plastycznego, w tym przypadku obroty w załomach.
Teoria linii załomów plastycznych wykorzystuje kinematyczne twierdzenie teorii nośności granicznej (plastycznej) o oszacowaniu górnym, tzn.: „Spośród wszystkich kinematycznie dopuszczalnych mechanizmów zniszczenia ten ejst rzeczywisty, który realizuje minimum energii układu „. Kinematycznie dopuszczalny mechanizm zniszczenia, to taki, który spełnia kinematyczne warunki brzegowe. Nie jest konieczne spełnienie jakichkolwiek innych warunków, w tym warunków statycznych (równowagi). Kinematycznie dopuszczalnych mechanizmów może być bardzo dużo, ale tylko jeden jest rzeczywisty – ten dla którego mnożnik nośności $\lambda$ jest najmniejszy. Na rys. 3 pokazano cztery mechanizmy zniszczenia płyty (rys. 1a), z których każdy jest kinematycznie dopuszczalny, bowiem płaty płyty mogą się tak przemieścić , by na podporach przemieszczenia były zerowe (są spełnione warunki kinematyczne). Dla schematu 3d) mnożnik obciążenia jest najmniejszy i jest to schemat najbliższy rzeczywistemu. Można pokazać, że jest to schemat rzeczywisty.
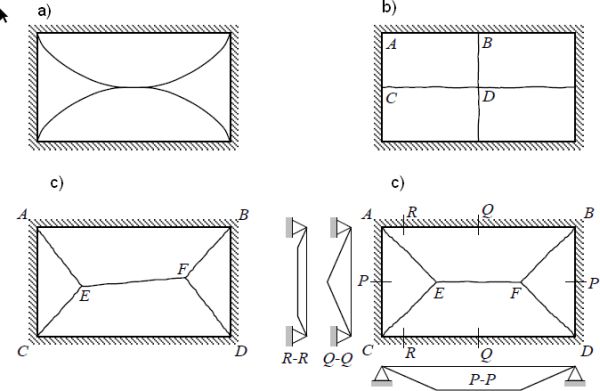
Rys.3. Kinematycznie dopuszczalne mechanizmy zniszczenia płyty z rys. 1a: a) kołowe linie załomów, b) proste linie załomów przechodzące przez punkty A-B-C_D, c) daszkowy mechanizm zniszczenia z liniami załomu A-B-D-C-A, A-E,C-E,E-F, F-F, F-F, d) daszkowy mechanizm zniszczenia dla linii E-F równoległej do A-B [6]
W teorii linii załomów słuszna jest zasada mocy wirtualnych
| $ \delta \dot{W}= \delta \dot {L}$, | (1) |
gdzie $\dot{W}$ jest mocą sił zewnętrznych, a $ \dot{L}$ mocą sił wewnętrznych. Zasadę (1) można uzyskać poprzez przeróżniczkowanie po czasie uniwersalnej zasady prac wirtualnych, którą można zapisać w postaci [7], s. 406 :
| $ \delta W= \delta L$, | (2) |
gdzie $\delta L$ jest wirtualną pracą sił zewnętrznych, a $\delta W$ wirtualną pracą sił wewnętrznych. W analizie procesów inżynierskich nie będziemy prowadzić analizy w czasie wystarczy nam posługiwanie się zasadą prac wirtualnych (2). Zasada (2) obowiązuje dla każdego mechanizmu plastycznego, pokazanego na rys. 3.\
W praktyce dla kinematycznie dopuszczalnych mechanizmów, będziemy badać równanie prac:
| $W=L$, | (3) |
Wykazuje się, że analizę mechanizmów plastycznych można dokonać jak dla ciał sztywno-plastycznego, to znaczy dla takiego, w którym nie jest istotne zachowanie sprężyste. Przyjmuje się, ze kąty obrotu $\varphi$ są małe i pomija się geometryczne efekty nieliniowe.
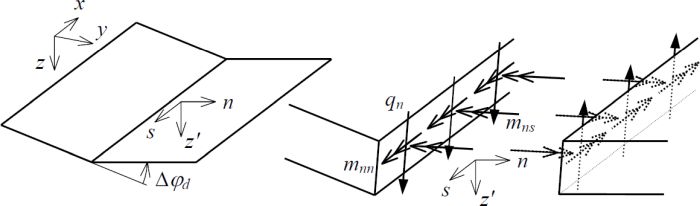
Rys. 4. Odkształcenia i siły płytowe w linii załomu [6]
Na rys. 4 płytę umieszczono w układzie globalnym kartezjańskim $(x,y,z)$; każdy płat ma lokalny układ $(n,s,z’)$, gdzie $n, s$ jest odpowiednio normalną i styczną do linii załomu.
Zakłada się, że odkształcenia plastyczne w całości koncentrują się w załomach plastycznych i są mierzone kątem obrotu $\Delta \varphi_d $ sąsiednich płatów względem siebie(rys.4). Obroty w liniach załomów są spowodowane momentami zginającymi $m_{nm}$ powstałymi w tych liniach Siły płytowe : moment skręcający $m_{ns}$ i siła poprzeczna $q_n$ są pomijane Do uplastycznienia przekroju płyty musi w nim wystąpić moment $m_{p} $ równy nośności plastycznej, to znaczy nośności przegubu plastycznego:
| $ m_{nm}=+m_p$, jeśli $\Delta \varphi_d > 0$, $ m_{nm}=-m_p$, jeśli $\Delta \varphi_d < 0$ |
(4) |
Przykłady obliczeniowe
Płyta prostokątna podparta przegubowo obciążona równomiernie
Metodą linii załomów wyznaczymy nośność płyty prostokątnej podpartej przegubowo i obciążonej powierzchniowo, stałym obciążeniem $p$. Płyta jest izotropowa i stałej długości, więc moment plastyczny $m_{pi}$ linii załomu jest taki sam dla wszystkich załomów.
Płytę ABCD o wymiarach axb podzielono na cztery płaty 2x(1)+2x(2)w sposób pokazany na rys.5 Przyjęty przebieg linii załomów spełnia kinematyczne warunki brzegowe dla różnych położeń $x$ punktu E i F.
Zwykle siatkę załomów w płycie wielokątnej przyjmuje się z „rozwiązania dachu”, to znaczy w narożach według dwusiecznej kąta, a kalenice na połączeniu punktów przecięcia dwusiecznych sąsiednich naroży. Niżej pokażemy, że taka siatka załomów jest wystarczająca (do oszacowania nośności płyty) tylko dla szczególnych przypadków (np. płyty kwadratowej), choć jest poprawna (spełnia kinematyczne warunki brzegowe) i może stanowić pierwszą iterację siatki załomów. W przypadkach inżynierskich często na tej pierwszej iteracji zostaje zakończony proces wyznaczania nośności płyty i w tym przypadku należy zdawać sobie sprawę, że błąd oszacowania nośności może być nawet kilkudziesięcio-procentowy.
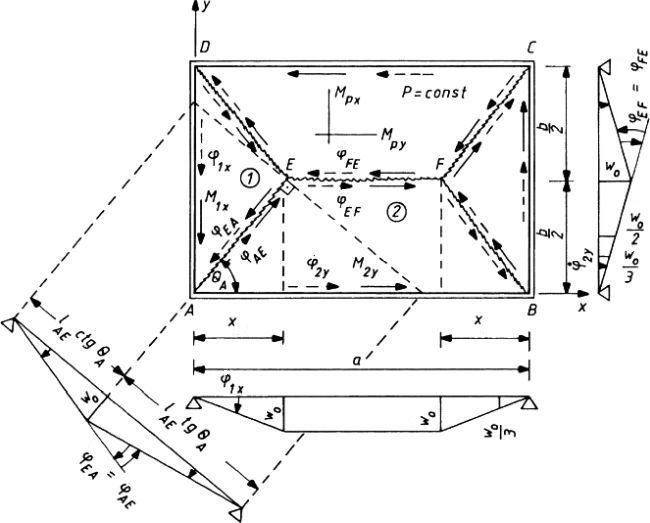
Rys. 5 Płyta do przykładu 1.2.1. (zmodyfikowane [3], str. 173 )
Mechanizm plastyczny uruchamiamy poprzez pionowy ruch punktu E i F o $w_0$ w dół.
Wówczas praca sił zewnętrznych $\int \limits_A (p \cdot w) dA $ na płacie (1) wyniesie
| $L_1=\dfrac{w_0}{3} \cdot \dfrac{1}{2}b \cdot x \cdot P$, |
gdzie: $\dfrac{w_0}{3}$ jest przemieszczeniem pionowym środka geometrycznego płata (1), a $\dfrac{1}{2}b \cdot x \$ – polem powierzchni tego płata.
Praca sił zewnętrznych na płacie (2) wynosi:
| $L_2=2 \dfrac{w_0}{3} \dfrac{1}{2} \dfrac{b}{2} x \cdot P+\dfrac{w_0}{2}(a-2 x) \dfrac{b}{2}p$, |
Całkowita praca sił zewnętrznych wyniesie:
| $L=2(L_1+L_2)= \dfrac{w_0}{6} p b(3a-2x)$, |
Praca sił wewnętrznych $W=\sum \limits_i \varphi_i m_{pi} l_i$, jest sumą pracy momentów plastycznych $m_{pi}$ w załomach (i)-tych o długości $l_i$ na kątach obrotu płatów względem siebie $\varphi_i $. Dla płyty izotropwej $m_{pi}=const=m_p$, a dla poszczególnych linii załomów mamy:
dla $i=EF$ :
$\varphi_{EF}=\dfrac{w_0}{b/2}+ \dfrac{w_o}{b/2}= \dfrac{4w_0}{b}$ ,
$W_{EF}=m_p \cdot l_{EF} \cdot \varphi_{EF}= m_p (a-2x) \dfrac{4w_0}{b}$.
dla $i=AE$:
$\varphi_{AE}=\dfrac{w_0}{l_{AE}}\left[ ctg\theta_A+ ctg(\pi/2-\theta_A)\right]$ ,
$ ctg \theta_A=\dfrac{x}{b/2}$,
$ctg (\pi/2-\theta_A)=tg \theta_A=\dfrac{b/2}{x}$,
$l_{AE}=\sqrt{x^2+(b/2)^2}$,
$W_{AE}=m_p \cdot l_{AE} \cdot \varphi_{AE}= m_p \cdot \left ( \dfrac{b}{2x_1}+\dfrac{2x_1}{b} \right) w_0$.
Praca sił wewnętrznych we wszystkich załomach wynosi:
$W=4W_{AE}+W_{EF}=2m_p \left ( \dfrac{b}{x}+\dfrac{2a}{b}\right) w_0$.
Z równania prac (3) $W=L$, mamyoszacownw kinematyczne (lub gopne nośności płyty $ p_{pl}$:
| $ Pp_{pl}=\dfrac{12 m_p}{b^2}\dfrac{b^2 +2 a x}{x(3a-2x)}$, | (5) |
w funkcji zmiennej $x$ określającej położenie linii załomów (rys.5).
Formuła (4) jest oszacowaniem kinematycznym (od góry) obciążenia $p_{pl}$ dla różnych linii załomów. Rodzina linii załomów ma kształt jak na rys. 5, ale punkty E i F mogą być położone na linii od krawędzi płyty (AD i CB) aż do $b/2$. Najlepsze oszacowanie uzyska się dla takiej wartości $x$ dla której (5) przyjmuje wartość minimalną, tzn. dla warunku stacjonarnego minimum
| $ \dfrac{\partial p_{pl}}{\partial x}=0$ | (6a) |
Po wykonaniu przypisanych działań w (6) uzyskujemy równanie na wyznaczenie $x$:
| $ 4ax^2+4b^2x-3 a b^2=0$ | (6b) |
Pierwiastkiem równania (6b) jest
| $x=\gamma$\dfrac{b}{2} | (6c) |
gdzie $\gamma= \sqrt{3+{\dfrac{b}{a}}^2} -\dfrac{b}{a}$.
Oszacowanie kinematyczne nośności granicznej opisuje formuła
| $ p_{pl}=\alpha \dfrac{24 m_p}{b^2}$, gdzie $\alpha=\dfrac{1}{ \gamma^2}$ | (7) |
W tab.1 przedstawiono zależność położenia siatki załomów i nośności granicznej płyty prostokątnej od stosunku wymiarów płyty b/a. W klumnie 2 podano współczynnik kształtu $\gamma$ (6d), w kolumnie 3 – położenie węzła siatki załomów (6c), a w kolumnie 4 – współczynnik obciążenia granicznego $\alpha$ (7b)
Tab.1. Zależność lokalizacji siatki załomów i nośności płyty od jej stosunku wymiarów b/a
 Dla płyty kwadratowej x=b/2 obciążenie graniczne jest największe. Nośność płyty spada wraz ze zmniejszaniem się stosunku a/b. Dla b=a/3 osiąga ok. 50%wielkości maksymalnej, a jednocześnie $x=0,72 b$.
Dla płyty kwadratowej x=b/2 obciążenie graniczne jest największe. Nośność płyty spada wraz ze zmniejszaniem się stosunku a/b. Dla b=a/3 osiąga ok. 50%wielkości maksymalnej, a jednocześnie $x=0,72 b$.
Płyta prostokątna obciążona siła skupioną
Na rys.6 pokazano siatkę linii załomów oraz zależności geometryczne dla płyty protokątnej axb, o przekątnej d, obciążonej siła skupioną Q w środku
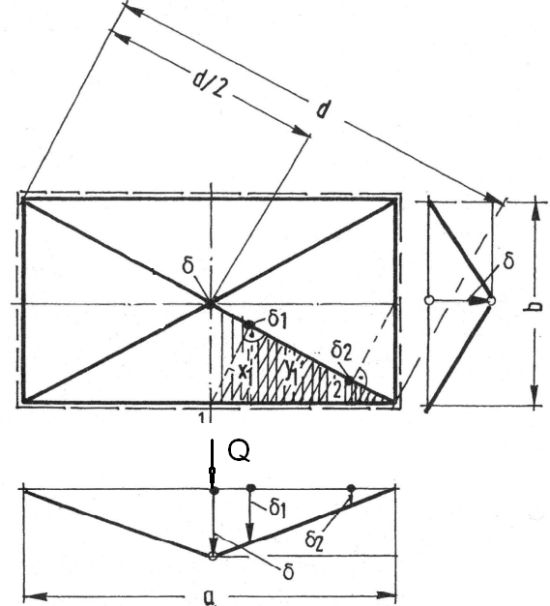
Płyta do przykładu 1.2.2 [2], rys. 131
Praca siły P wynosi
| $ L=Q \cdot \delta$, | (8) |
gdzie $\delta$ jest wirtulanym przemiszczeniem środka płyty (pod siłą $P$. Przemieszczenie $\delta_1$ punktu wzdłuż linii załomu można wyznaczyć z zależności:
| $\delta_1= \dfrac{y_1}{d/2}\cdot \delta$, | (9a) |
przy czym spełnione są stosunki:
| $\dfrac{\delta_1}{x_1}= \dfrac{y_1}{x_1}\cdot \dfrac{2}{d}\cdot \delta$, $\dfrac{y_1}{x_1}=\dfrac{a/2}{b/2}=\dfrac{a}{b}$ $\dfrac{\delta_1}{x_1}=\dfrac{a}{b}\cdot \dfrac{2\delta}{d}= const$ |
(9b) |
Przemieszczenie $\delta_2$ w pobliżu naroża spełnia warunek:
| $\dfrac{\delta_2}{x_2}= \dfrac{b}{a}\dfrac{2 \delta}{d}$, | (9c) |
Długość linii załomu wynaczamy z zależności
| $\dfrac{1}{2} \sqrt{a^2+b^2}$, | (10) |
Praca sił wewnętrznych wynosi
| $W=-4 m_p\cdot {1}{2}\sqrt{a^2+b^2}\cdot \left ( \dfrac{a}{b}+\dfrac{b}{a}\right) \cdot \dfrac{2\delta}{\sqrt{a^2+b^2}} =-4 \dfrac{a^2+b^2}{ab} \delta \cdot m_p$, | (11) |
Z równania prac$l=W$ , otrzymujemy oszacownie górne nośnosci plastycznej Q_{pl} [2], (208) :
| $ Q_{pl}=4 \dfrac{a^2+b^2}{ab}\cdot m_p$, | (12a) |
| dla płyty kwadratowej (a=b) $ \to Q_{pl}=8 m_p$, | (12b) |
Płyta obciążona siłą skupioną w pobliżu krawędzi
Interesującym mechanizmem zniszczenia jest mechanizm kołowy, pokazany na rys. 6, przyjmowny przy analizie nośności granicznej płyty obciążonej siła skupiona w pobliżu krawędzi.
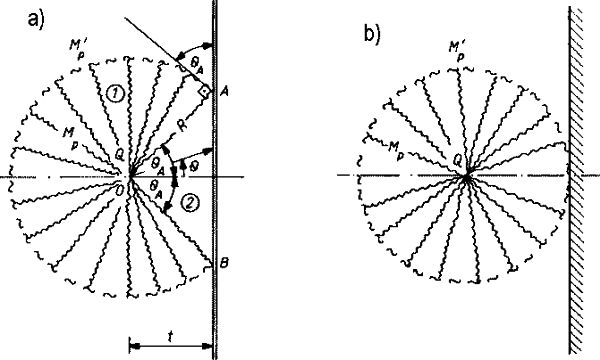
Rys. 7 Płyta do przykładu 1.2.3 [3], str. 190
Dzialanie sily skupionej Q, przyłożonej w pobliżu przegubowo podpartej prostliniowej krawędzi płyty może wywołać siatkę załomów, pokazaną na rys. 6a. W przypadku krawędzi utwierdzonej (rys.6b) okrąg załomów wjst styczny do krawędzi.
Można wykazać, że oszacoweanie górne (kinematyczne obciążenia granicznego w przypadku płyty izotropowej, wynosi [3],190 :
| dla przypadku rys 6a: $Q_k=(3 \pi+2) m_p =11,42 m_p $
dla przypadku rys 6b: $Q_k=4 \pi m_p =12,56 m_p $, |
(13a)
(13b) |
gdzie $m_p=(M_p)= \dfrac{f_y b h^2}{4}$ jest nośnością plastyczną przekroju płyty na jednostkę długości załomu.
Promień okręgu załomów $R=t/ cos \theta_A= const$, a $\theta _A= 45^0$
Połączenia konstrukcji
Mechanizmy zniszczenia blachkonstrukcji mogą być modelowane eopatrzomymi w pkt 1.2 przypadkami podstawowymi, aminowicie liniami załomów „daszkowych” (rys. 7a oraz kołowych (rys.8b)
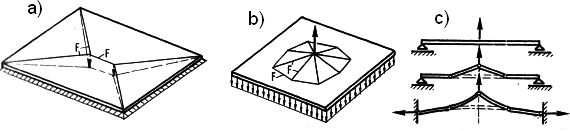
Rys.8 Siatki załomów przy zniszczeniu blach stalowych. F-linie załomów: a) linie załomów niekołowe, b) załomy kołowe, c) belkowa analogia zniszczenia [2], str. str. 255
Takie podejście jest przedmiotem normy [1] . Rozpatruje się zastępcze króćce teowe (p. rys.1). w strefie rozciagania blach wyciągane przez śruby (rys. 8b,c) lub poprzeczne żebra, albo też w strefie ściskania , najczęściej poprzez docisk blachy podstawy słupa do powierzchni betonowych fundamentów (rys. 9). Najważniejszym parametrem do wyznaczania nośności zastępczego krtóćca tefgowego ejst długośc efektywna $l_{eff}$.
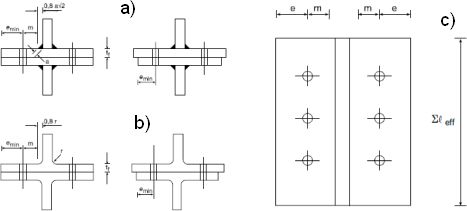
Rys.9 Parametry T-króćca a) linie załomów niekolowe, b) załomy kołowe, c) belkowa analogia zniszczenia
[1], rys. 6.2
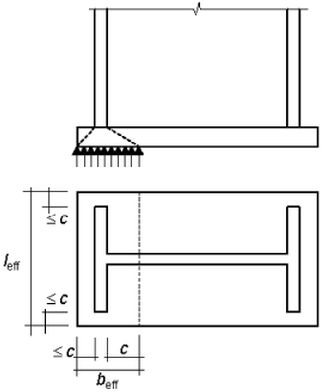
Rys.10 T-króciec podstawy słupa oraz szerokość efektywna $b_{eff}$ [1], rys. 6.4
Długość $l_{eff}$ lub szerokość $b_{eff}$ efektywna są zastępczymi wielkościami nie znajdujące interpretacji fizycznej. Najczęściej są wyznaczane w badaniach eksperymentalnych lub numerycznych w zależności od sytuacji projektowej i następnie dopasowywane do prostych formuł analitycznych. Najważniejsze sytucje zostaną pokazane w kolejnych punktach.
Śrubowe połączenia czołowe
Mechaznimy zniszczenia blachy czołowej połączenia belki dwutoeowej ze słupem pokazano na rys. 11. Rys. 11 b i c przedstawia mechanizm zniszczenia półki słupa, a rys. 11d jeden z mechanizmów zniszczenia blachy czołowej belki. Na rys 11 e/i pokazano inne mechanizmy zniszczenia blachy czołowej.
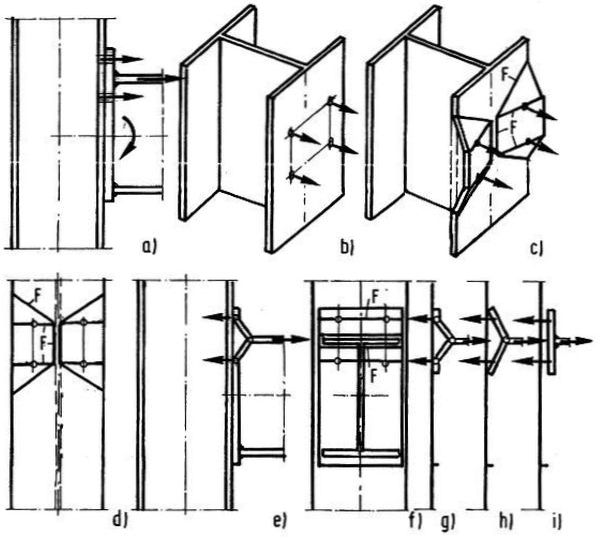
Rys.11 Mechanizmy zniszczenia blach czołowych połączenia śrubowego F-linie załomów: a) konstrukcja, b, schemat działania sił w śrubach, c) przestrzenne linie załomów w pasie słupa, d)-i) schematy mechanizmów zniszczenia blachy czołowej połaczenia [2], str. 255
Przykłady rachunkowe
Przykład rachunkowy śrubowego połaczenia czołowego niesprężanego podano w artykule – przykład 6.5.
Literatura
- PN-EN 1993-1-8 +Ap1+AC:2006, Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
- Petersen C. (2013), Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
- Wojewódzki W. J. (2006), Nośność graniczna płyt. Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa
- Gvozdev A. A. (1949), Teoria predelnovo ravnoviesja, Strjizdat, Moskva
- Johansen K. W. (1949), Pladeformler (2nd ed.). Polyteknisk Foregning
- Vrouwenvelder A. C. W. M., Witteveen J. (2003), The plastic behaviour and the cal-culation of plates subjected to bending (Civil Engineering Masters Course Plasticity Ct 4150). TU Delft
- Piechnik S. (2007), Mechanika techniczna ciała stałego, Wydawnictwo Politechniki Krakowskiej, Kraków
________________________________




