Leszek Chodor, 12 listopada 2014
04-03-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 3 Czytelników
Konstrukcje cięgnowe są dziś synonimem nowoczesności: celowości i logiki dzieła – jako wymóg ekonomiczności i zamierzenia natury i stosowane do pokonywania wielkich rozpiętości. [1]. Konstrukcje cięgnowe są stosowane miedzy innymi w: mostach wiszących i powieszonych, halach widowiskowo-sportowych, pawilonach wystawowych, dworcach i hangarach, masztach i kominach z odciągami, wyciągach narciarskich i kolejkach linowych, napowietrznych liniach energetycznych, urządzeniach do transportu ludzi i materiału [2]. Konstrukcje cięgnowe coraz częściej występują wraz z przekryciami membranowymi, wykonanymi z nowoczesnych, trwałych i wytrzymałych materiałów tekstylnych – tkanin technicznych.
Konstrukcje cięgnowe znamienne są tym, że pojedyncze cięgno (lina) doskonale nierozciągliwe i nieskończenie wiotkie o niezerowej masie swobodnie zwisające pomiędzy dwiema podporami w jednorodnym polu grawitacyjnym, przyjmuje prosty kształt krzywej łańcuchowej, danej równaniem:
$$\begin{equation} y=a \cdot cosh \left(\cfrac{x}{a}\right)\label{1} \end{equation}$$
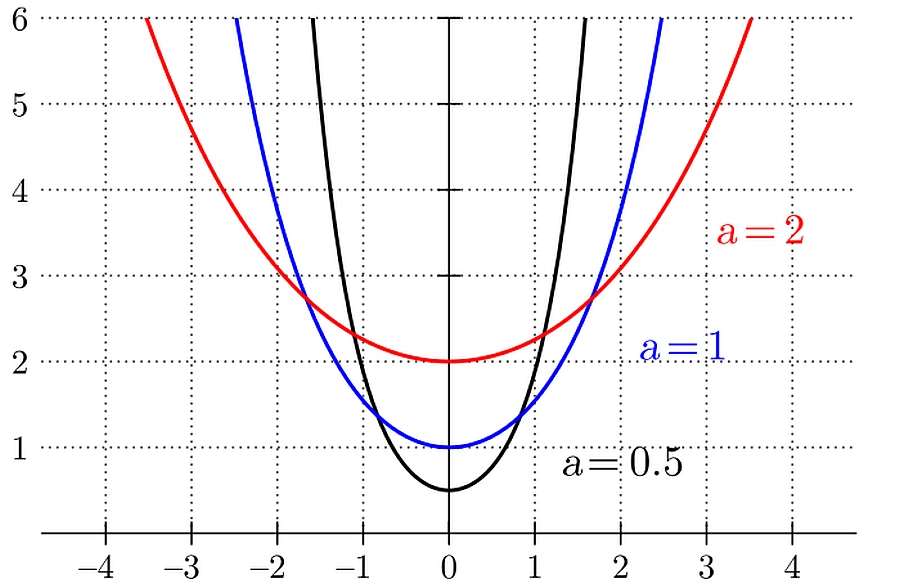
Rys.1. Krzywa łańcuchowa [3]
W równaniu krzywej łańcuchowej ($\ref{1}%) i na rys. 1 x, y są współrzędną i rzędną, natomiast a zależy od warunków brzegowych i jest rzędną najniższego punktu krzywej.
Krzywa łańcuchowa jest przedmiotem wielu opracowań, np: [4], [5], [6]. W opracowaniach tych wyczerpująco przedstawiono sens fizyczny i mechaniczny krzywej lańcuchowej. Wyprowdzenie równanie cięgna (krzywej łańcuchowej, zwanej też katenoidą) przedstawiono w rozdziale Cięgno_uklada_się_w_krzywa_lancuchowa_( katenoide).
Wprowadzenie
Przekrycia konstrukcjami cięgnowymi są często połączone z materiałami membranowymi, a utworzone w ten sposób konstrukcje cięgnowo-membranowe od 40-tu lat nabierają coraz większego znaczenia w architekturze i inżynierii w tym w przekryciach hal i galerii.
Na rys. 2 przedstawiono przykład realizacji przekrycia cięgnowo-membranowego w amfiteatrze widowiskowym, na rys.3 zadaszenie na dworcu PKP we Wrocławiu, na rys.4 zadaszenie hali wystawowej, a na rys. 5 zadaszenie hali magazynowej.

Rys.2. Zadaszenie cięgnowo-membranowe amfiteatru Kadzielnia w Kielcach [7]

Rys.3. Zadaszenie cięgnowo -membranowe na dworcu PKP we Wrocławiu [8]

Rys.4. Kopuła hali wystawowej Millenium Dome w konstrukcji cięgnowo-membranowej [9]

Rys.5. Przekrycie membranowe hali sportowej [10]
Konstrukcje cięgnowe
Typy, podstawowe zalety i wady konstrukcji cięgnowych
Zastosowania konstrukcji cięgnowych umożliwia: dużą swobodę w kształtowaniu bryły budynku, możliwość otrzymania dużej rozpiętość i powierzchni i niewielki ciężar konstrukcji, który zawdzięczamy wysokiej wytrzymałości materiału jak też występowania w cięgnach optymalnego układu sił, czyli wyłącznie sił rozciągających. Niestety lekkość samego układu cięgnowego dla równowagi prowadzi do: dużych obciążeń fundamentów i bloków kotwiących, skomplikowanego wykonawstwa ze względu na konieczność ustalenia właściwej geometrii i stężenia ustroju, a także sprężenia i kotwienia cięgien pod dużym naciągiem.
W praktycznych sytuacjach należy użyć bardzo specjalistycznego sprzętu z wysokokwalifikowanym i doświadczonym zespołem inżynierów oraz techników. Z powodu bardzo silnych nieliniowości geometrycznych klasyczne metody projektowania zawodzą i należy stosować metody półodwrotne (zgadywania poprawnej geometrii i sprężania cięgien, a następnie sprawdzania podstawowych równań teorii sprężystości (Navier’a, Cauchy’ego i Hooka). Kolejne iteracje prowadzone są ręcznie z użyciem programów komputerowych. Takie obliczenia są żmudne, wymagają dobrej znajomości teorii oraz zachowania konstrukcji linowo-membranowych i są prowadzone przez wyspecjalizowane ośrodki i inżynierów.
Kształty dwukrzywiznowych przekryć cięgnowych rozpięte są najczęściej na powierzchniach II stopnia (kwadryki), powierzchniach prostokreślnych lub innych (np. helikoidzie, konoidzie, kuboidzie, powierzchni Scherka czy Peano). (p. artykuł kopuła siatkowa)
Podstawowe rodzaje konstrukcji cięgnowych , to:
Pojedyncze cięgna, gdzie elementem nośnym są pojedyncze cięgna, tworzące wiązkę cięgien ułożonych równolegle lub radialnie i zakotwionych w konstrukcji wsporczej. Zabezpieczając strukturę przed ujemnymi wpływami ssania wiatru, pokrycie musi mieć duży ciężar własny, co zmniejsza walory ekonomiczne.
Płaskie wiązary cięgnowe zwane też kratownicami (dźwigarami) Jawertha, w których zastosowano cięgna napinające pojedyncze cięgna (nośne), otrzymując napięty płaski dźwigar cięgnowy. Napięcie znacznie ogranicza przemieszczenia wywołane nierównomiernym obciążeniem oraz poprawia wrażliwość ustroju na drgania wywołane porywami i ssaniem wiatru.
Powierzchniowe siatki cięgnowe, składają się z cięgien: nośnych i napinających rozpiętych na zakrzywionej powierzchni w odróżnieniu od wiązarów płaskich. Obydwa rodzaje cięgien są kotwione w dźwigarze brzegowym, który oprócz oparcia na fundamencie przytrzymywany jest na obwodzie słupami lub odciągami.
Szczególnym rodzajem konstrukcji cięgnowych są:
Mosty wiszące , odznaczają się bardzo elastyczną formą. Ustrój nośny stanowią dwa kable wsparte na wysokich pylonach do którego zostaje podwieszany najczęściej żelbetowy lub stalowy pomost.
Mosty podwieszane (zwane wantowymi) są formą przejściową pomiędzy mostem tradycyjnym a mostem wiszącym. Ustrój nośny stanowią ukośne liny (rozmieszczone na ogół w kształcie wachlarza) zamocowane do wysokich pylonów, których kształty mogą być bardzo zróżnicowane. W tab 1 zestawiono podstawowe rodzaje przekryć cięgnowych.
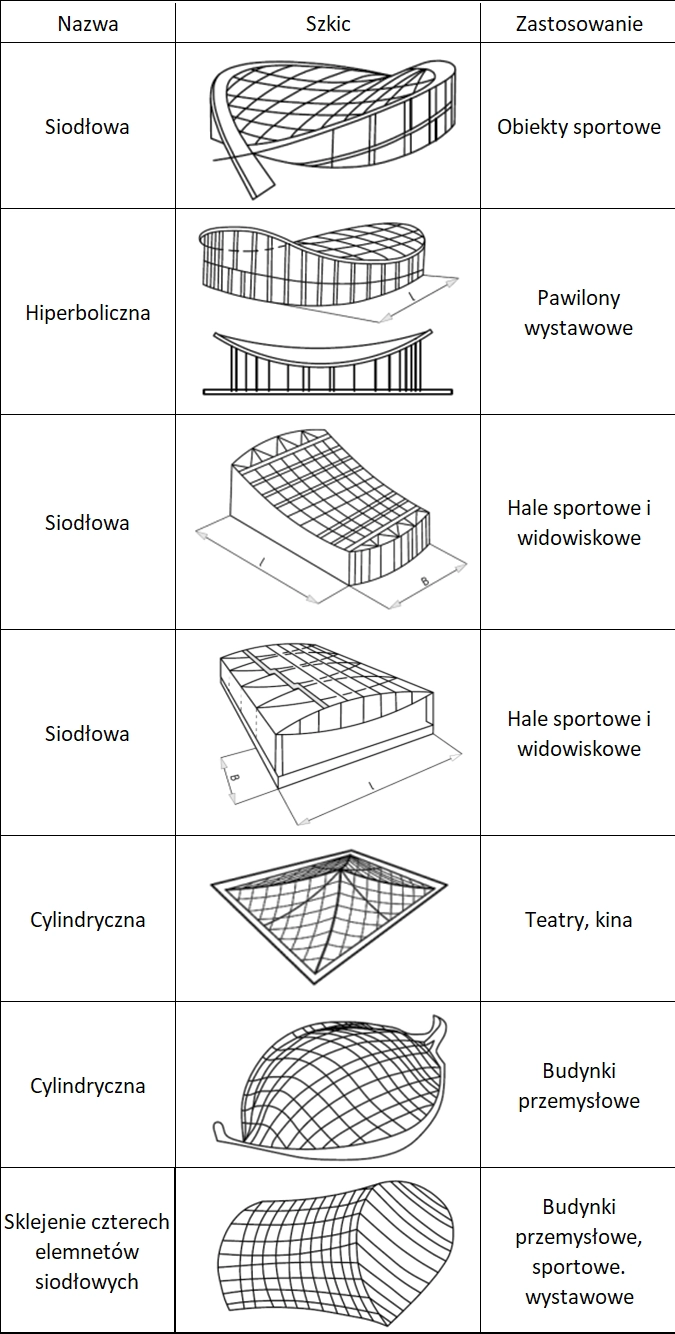
Najczęściej stosowane rodzaje powierzchni z rozpiętymi cięgnami zestawiono w tab.1.
Tab.1. Podstawowe rodzaje przekryć cięgnowych (opracowano na podstawie [11])
Cięgna
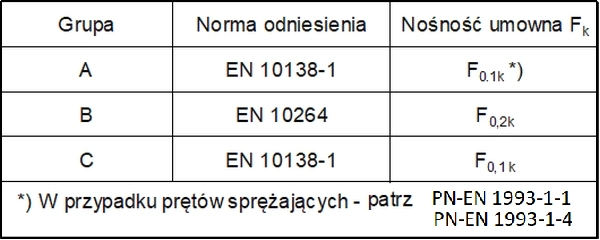
Cięgna są elementami o dużej nośności na rozciąganie i niewielkiej sztywności na zginanie, to znaczy nie przenoszą momentów zginających oraz sił ściskających. Cięgna, zbliżone do ideału pod względem małej sztywności na zginanie, nazywane się cięgnami wiotkimi, wykonywanymi jako druty lub splotki w trzech grupach A, B i C (tab. 2). Cięgna sztywne wykonane z kształtowników stalowych i obciążone siłami rozciągającymi zdolne są przenosić również momenty zginające, ale jest to traktowane pobocznie i z reguły prowadzi do zmniejszenia efektywności materiałowej elementu.
Tab.2. Grupy i rodzaje cięgien [12]-tab. 1.1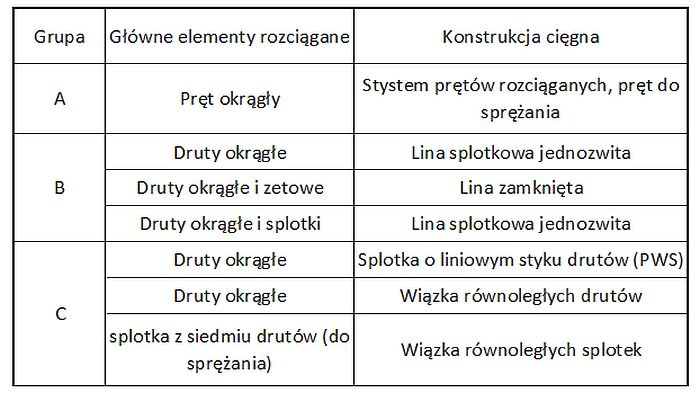
Cięgna poprzez zastosowanie specjalnych połączeń z konstrukcją, powinny być przystosowane do regulacji i wymiany podczas eksploatacji budowli w którą są wbudowane. Wymóg ten sprawia, że cięgna są na ogół prefabrykowane i dostarczane na budowę łącznie z konstrukcją wsporczą. Właśnie takie regulowane i wymienialne cięgna są przedmiotem podstawowej normy do projektowania konstrukcji cięgnowych [12].
Cięgna, które nie spełniają wymogu regulacji i wymienności stosowane są głównie w mostach podwieszanych lub mostach sprężanych i z reguły nie są stosowane w przekryciach budowli.
Do wyrobów grupy A wg tab.2, zalicza się się również pręty okrągłe zakończone gwintem (stężenia dachów, ścian i dźwigarów, odciągi dachów i pylonów, systemy cięgien do kratownic drewniano-stalowych oraz konstrukcji stalowych płaskich i przestrzennych).
Cięgna grupy B składają się z drutów, których końce są zakotwione w tulejach zaciskowych lub innych końcówkach i są produkowane w zakresie średnic od 5 mm do 160 mm [13].
Cięgna grupy C wymagają indywidualnego lub zbiorczego zakotwienia i szczególnej ochrony przed korozją.
Liny splotkowe jednozwite stosuje się jako: odciągi masztów antenowych, kominów przemysłowych, innych masztów i mostów; cięgna nośne i brzegowe w konstrukcjach lekkich; wieszaki lub cięgna główne w mostach podwieszonych ; cięgna stabilizujące w siatkach cięgnowych oraz kratownicach. Liny zamknięte stosuje się w zakresie średnic od 20 do 180 mm, głównie na: odciągi i cięgna główne w konstrukcjach mostowych; cięgna główne i stabilizujące w kratownicach cięgnowych; odciągi pylonów i masztów; cięgna brzegowe w siatkach cięgnowych. Liny splotkowe stosuje się jako: odciągi masztów; wieszaki w mostach podwieszonych; cięgna tłumiące i stabilizujące pomiędzy odciągami; cięgna brzegowe w membranach z tkanin. Wiązki równoległych splotek stosuje się jako odciągi w mostach stalowych i zespolonych, cięgna główne w mostach podwieszonych oraz zewnętrzne.
Splotka (żyła) jest elementem liny, składającym się z drutów o odpowiednim kształcie i wymiarach, splecionych helisoidalnie w tym samym lub przeciwnych kierunkach, w jednej lub kilku warstwach wokół rdzenia. Lina splotkowa (wielozwita) jest zespołem splotek splecionych helisoidalnie w jednej (lina jednowarstwowa) lub kilku warstwach wokół rdzenia lub środka (lina nieodkrętna lub o równoległym ułożeniu splotek). Lina jednozwita (spiralna) jest zespołem co najmniej dwóch warstw drutów splecionych helisoidalnie wokół drutu centralnego. Lina zamknięta jest liną jednozwitą z zewnętrzną warstwą prętów zetowych. Cięgno jest głównym elementem rozciąganym w konstrukcji (np. w moście wantowym) i składa się z liny, splotki lub wiązki równoległych drutów lub splotek.
Na rys. 7 pokazano najczęściej występujące rodzaje lin stalowych.

Rys.7. Rodzaje lin stalowych: a) splotkowa (wielozwita), b) spiralna zwarta, c) spiralna zamknięta, d) kabel złożony z pojedynczych drutów lub lin
Do oceny trwałości cięgien stosuje się klasy ekspozycji podane w tab.3
Tab.3. Klasy ekspozycji cięgien [12]-tab.2.1.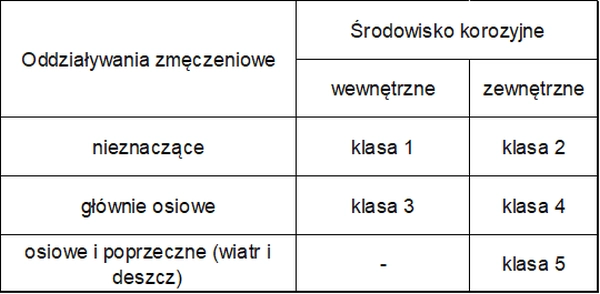
Ciężary jednostkowe i współczynniki wypełnienia najczęściej stosowanych lin zestawiono w tab.4. Współczynnik wypełnienia jest to stosunek sumarycznego nominalnego pola przekroju wszystkich drutów do pola wewnątrz obrysu, opartego na nominalnej średnicy liny. Ciężar jednostkowy jest ciężarem własnym jednostkowego odcinka liny, uwzględniający ciężar przekroju metalowego wraz z zabezpieczeniem antykorozyjnym.
Tab.4. Ciężary jednostkowe i współczynniki wypełnienia lin [12]-tab.2.2.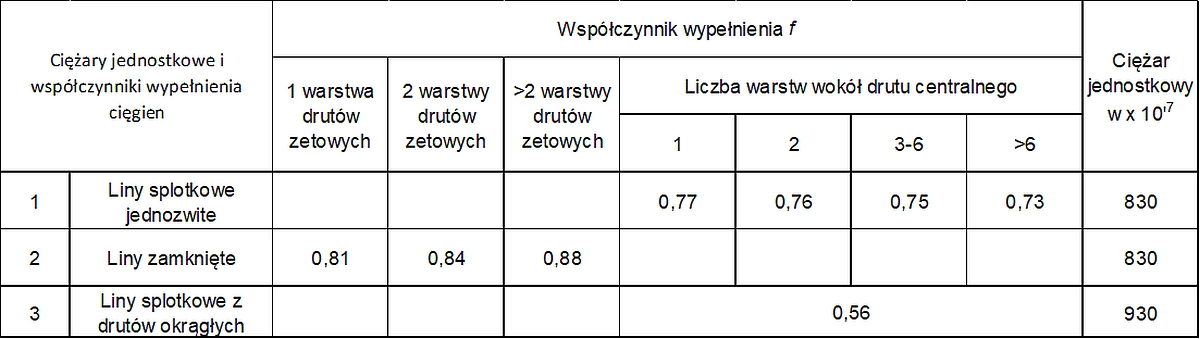
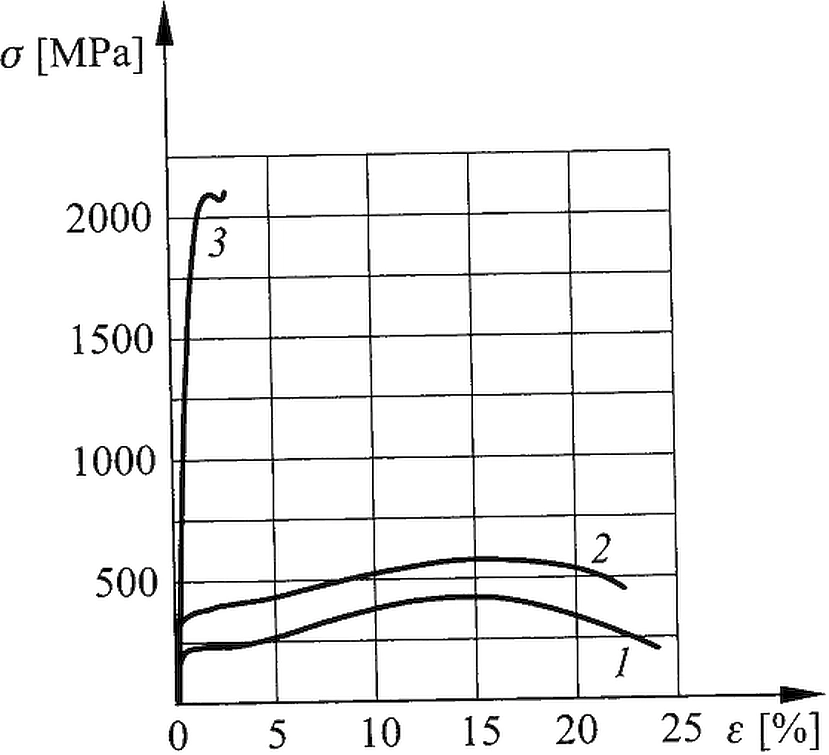
Rys.8. Charakterystyka wytrzymałościowe różnych stali: 1 – stal S235, 2- stal S355, 3- stal na druty lin
Na rys.8 porównano charakterystykę wytrzymałościową typowe druta na liny z charakterystyką stali S235 i S355. Stal na druty lin ma wielokrotnie wyższą wytrzymałość od stali konstrukcyjnej.
Wytrzymałość charakterystyczną $f_y$ i $f_u$ dla stali konstrukcyjnej oraz $f_{0,2}$ lub $f_{o,1}$ i $f_u$ dla drutów przyjmuje się jak następuje:
dla stali zgodnie z [14],
dla drutów zgodnie z [15], {{PN-EN 10264-3:2012, Drut stalowy i wyroby z drutu -Drut stalowy na liny -Część 3: Drut okrągły i kształtowy ze stali niestopowej do pracy w trudnych warunkach obciążenia}} i [16],
dla lin zgodnie z [17], [18],
dla zakończeń lin stalowych zgodnie z [19],
dla splotek zgodnie z [20].
Zalecane kategorie wytrzymałościowe lin są następujące:
druty stalowe okrągłe Rr=1770 MPa,
druty stalowe zetowe Rr=1570 MPa,
druty okrągłe ze stali nierdzewnej Rr=1450 MPa.
Wytrzymałość liny jest stowarzyszona z minimalną siłą zrywającą linę Fmin, ale niekoniecznie odpowiada wytrzymałości drutów na rozciąganie.
Moduły sprężystości cięgien można przyjmować następująco:
- cięgna grupy A: E=210,0 GPa, z wyjątkiem cięgien ze stali nierdzewnej, dla których należy stosować parametry wg [14],
- cięgna grupy B: na podstawie badań w zależności od poziomu naprężeń oraz od tego, czy cięgno było przeciągnięte oraz obciążone i odciążone,
- cięgna grupy C: wg [20],
Przy braku wyników badań doświadczalnych, w pierwszym przybliżeniu obliczeniowej procedury iteracyjnej dla cięgien grupy B i C, można przyjmować początkowy moduł sprężystości wg tab. 5.
Tab.5. Moduł sprężystości EQ odpowiadający obciążeniom zmiennym Q [12]-tab.3.1.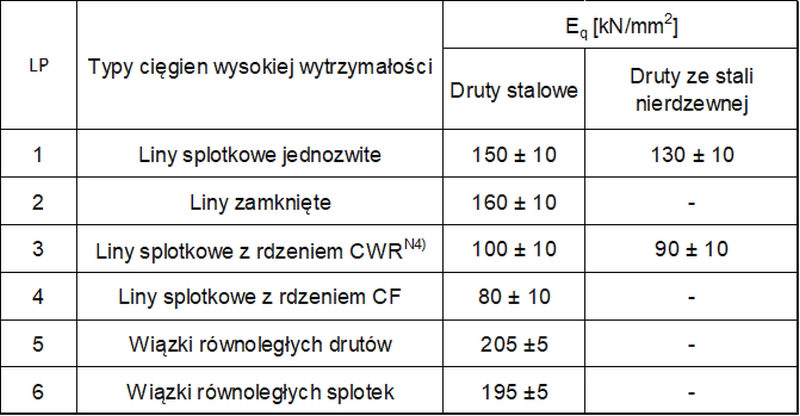
Dla lin zamkniętych moduł sprężystości E można przyjmować według wykresu, rys. 3.1. [12].
W przypadku analizy konstrukcji w trwałych sytuacjach obliczeniowych fazy eksploatacji stosuje się sieczny moduł sprężystości, wyznaczony w ten sposób, że bada się min 5 cykli obciążenia pomiędzy minimalną i maksymalną siła w cięgnie, wywołaną charakterystycznymi obciążeniami stałymi i zmiennymi.
Sztywności cięgien można wyznaczać, mnożąc moduł sprężystości E przez pole przekroju metalowego Am.
Cięgna grupy B należy przycinać na wymiar, ustalony dla określonego obciążenia zgodnie z pkt 3.4 , a długości i tolerancje wykonania należy ustalać zgodnie z pkt 3.5 [12]. Inne wymagania projektowe dla cięgien, w tym wymagania dotyczące transportu, przechowywania i montażu, terminologia i parametry cięgien stalowych, zakotwienia lin jednozwitych, i inne wymagania- podano w załącznikach A ,B i C do normy [12].
Współczynnik rozszerzalności termicznej przyjmuje się: αt=12·10-6/deg dla drutów stalowych ze stali konstrukcyjnej; αt=16·10-6/deg dla drutów stalowych ze stali nierdzewnej.
W przypadku próbek krótkich o długości mniejszej niż 10-krotna długość zwoju uwzględnia się to, że pełzanie próbki jest mniejsze niż w przypadku długiego cięgna. Przy braku dokładnych danych, efekt ten można uwzględnić, przygotowując krótsze cięgna o 0,15 mm na każdy metr długości.
Zakotwienia cięgien
- cięgien sprężających (nośnych i napinających),
- wieszaków,
- cięgien wantowych.
Od zakotwień cięgien oczekuje się aby umożliwiały naciąg cięgna, a po jego zakończeniu zapewniały trwałe przenoszenie siły w cięgnie (utrzymanie siły naciągu oraz długości cięgna) przez cały okres użytkowania elementu i ponadto powinny zapewniać dokładne wprowadzenie w cięgno siły o projektowanej wartości.
W każdej z grup wyróżnia się zakotwienia czynne i bierne. Zakotwienie czynne umożliwia naciąg drutów, splotów, prętów lub lin z możliwością regulacji siły. Zakotwienie bierne zapewnia utrzymanie pojedynczych drutów, splotów, prętów lub lin, ale bez możliwości regulacji naciągu. Zakotwienia cięgien sprężających dzielimy ponadto na zakotwienia cięgien z drutów sprężających, zakotwienia cięgien ze splotów sprężających oraz zakotwienia cięgien prętowych.
Najczęściej stosowane typy zakotwień cięgien zestawiono w tab 6.
Tab.6. Najczęściej stosowane typy zakotwień cięgien (opracowano na podstawie [23] z własnymi poprawkami i uzupełnieniami oraz wymianą ilustracji)
Analiza konstrukcji cięgnowych
Obciążenia konstrukcji cięgnowych
Ciężar własny cięgien wraz z elementami wyposażenia wyznacza się na podstawie przekroju poprzecznego i gęstości materiałów, chyba, że wartości te są określone w odpowiednich PN-EN 12385. W przypadku lin jednozwitych i zamkniętych oraz cięgien z drutów, charakterystyczny ciężar własny $g_k=w\cdot A_m$ wyznacza się dla składników metalowych i zabezpieczenia antykorozyjnego o łącznym ciężarze jednostkowym w. W przypadku cięgien grupy C, ciężar własny wyznacza się na podstawie ciężaru poszczególnych drutów lub splotek oraz ciężaru materiałów ochronnych (np. osłony HDPE, wosku, itd). Ciężary jednostkowe najczęściej stosowanych lin podano w tab.4.
Oddziaływanie wiatru w projektowaniu cięgien uwzględnia się jako efekty statyczne wynikające z oporu cięgien zgodnie z [24] oraz jako efekty dynamiczne i wzbudzanie, powodujące drgania cięgien. Najczęściej w przypadkach praktycznie spotykanych, złożonych kształtów siatek cięgnowych należy przeprowadzić badania modelowych w tunelu aerodynamicznym.
Obciążenie oblodzeniem należy przyjmować zgodnie z załącznikiem B i C do normy [25].
W obliczeniach uwzględnia się wpływ różnicy temperatur między cięgnem a konstrukcją. W przypadku cięgien w obiektach wolno-stojących wpływ różnicy temperatur uwzględnia się zgodnie z [26].
Aby zapobiec luzowaniu się cięgien i spadkowi naprężeń, co mogłoby doprowadzić do niekontrolowanej utraty stateczności i zmęczenia, a także spowodować uszkodzenia elementów nośnych i niekonstrukcyjnych – cięgna poddaje się wstępnemu sprężeniu, przez wymuszenie deformacji konstrukcji. W takich przypadkach na oddziaływania stałe składają się obciążenia grawitacyjne „G” oraz siły sprężające „P”, które zwykle traktuje się je jako pojedyncze oddziaływanie stałe „G+P” z odpowiednim współczynnikiem częściowym γGi.
Wstępny naciąg cięgien dobiera się tak, aby konstrukcja w warunkach wszystkich obciążeń stałych wykazywała oczekiwany (wymagany) stan odkształcenia i wytężenia, zgodnie z przyjętą geometrią. Stosuje się urządzenia do napinania i regulacji cięgien, przy czym wartość siły wstępnego naciągu w rozpatrywanej sytuacji traktuje się jako wartość charakterystyczną ze względu na interesujący stan graniczny. Jeśli nie wprowadza się regulacji cięgien, to zmienność sił wstępnego naciągu uwzględnia się w obliczeniach konstrukcji.
Wymianę co najmniej jednego cięgna traktuje się jako przejściową, a nagłą awarię cięgna traktuje się jako wyjątkową sytuację obliczeniową. Jeśli nie przeprowadza się dokładnej analizy, to można przyjąć, że efekt nagłej awarii cięgna odpowiada przyrostowi oddziaływań $E_d=1,5 \cdot (E_{d2}-E_{d1})$, gdzie $E_{d2}$ -wartość odpowiadająca stanowi po usunięciu cięgna, a $E_{d1}$ -wartość odpowiadająca stanowi przed awarią.
Obciążenia zmęczeniowe przyjmuje się zgodnie z zestawem norm PN-EN 1991.
Współczynnik tarcia miedzy liną, a stalowymi elementami wyposażenia (jak zaciski, siodła, uchwyty) wyznacza się na podstawie badań. Siły tarcia można redukować stosownie do redukcji średnicy cięgna w miarę wzrostu rozciągania.
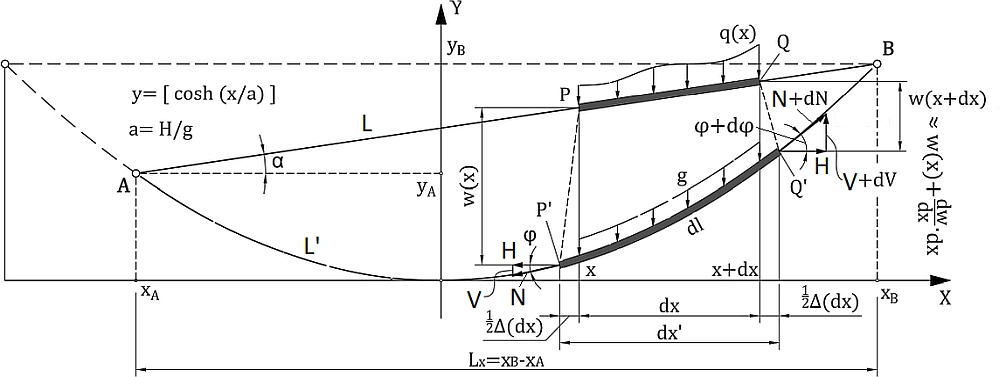
Równanie równowagi cięgna
Statyka pojedynczego cięgna była przedmiotem badań od czasów Galileusza [27]. Krótką notkę historyczną zamieszczono w artykule Krzywa łańcuchowa. Poniżej przedstawiono zagadnienie statyki cięgna w ujęciu [28] i w prosty sposób wyprowadzono równania katenoidy (krzywej łańcuchowej). W załączniku 1 zaprezentowano inne podejście, prowadzące do podobnej postaci równania cięgna.
Na rys. 9 pokazano pojedyncze cięgno zawieszone w punktach A i B (rys. 9a), zwisające pod obciążeniem $q_1$ w rzucie, czyli $q_2= \cfrac{q_1}{cos \alpha}$ po długości cięgna. Odcinek cięgna o długości $ds$, a w rzucie $dx=ds \cdot cos \alpha$ jest rozciągany siłą S na lewym i $(S+dS)$ na prawym końcu. Składowe sił $S$, to: pozioma $H=S \cdot cos \alpha$ i pionowa $T = S \cdot sin \alpha$.

Rys. 9 Schemat pojedynczego cięgna [28] – rozdz. 12, rys. 13
Warunki równowagi sił, działających na element $dS$ cięgna można zapisać w postaci:
$$ \begin{equation} \label{2} \begin {cases}
\textrm {$\sum H=0: $} & H-(H+dH)=0 \to dH=0 \to H=const \\
\textrm {$\sum M=0 $} & T dx – H dy=0 \to T=H y^{’} \to T^{’}=H y^{„} \\
\textrm {$\sum T (q_1)=0 $} &T-(T+dT)+ q_1 dx =0 \to T^{’} = q_1(x)\\
\textrm {$\sum T (q_2)=0: $} & T-(T+dT)+ q_2 ds =0 \to T^{’} = q_2(x) \cfrac{ds}{dx}\\
\end {cases} \end{equation} $$
Z porównania $(\ref{2}a) = (\ref{2}c)$ mamy
$$ \begin{equation} H y^”=q_1(x) \label{3} \end{equation} $$
Ponieważ $ds= \sqrt{dx^2 + dy^2}=dx \sqrt{1+{y^{’}}^2}$, więc po złożeniu $( \ref{2}b)$ i $( \ref{2}d )$, mamy:
$$ \begin{equation} H y^”=q_2(x) \sqrt{1+{y^{’}}^2}\label{4} \end{equation} $$
Długość odcinka liny wynosi
$$ \begin{equation} L= \int \limits_l \sqrt{1+{y^{’}}^2} \label{5} \end{equation} $$
Równanie różniczkowe $(\ref{3})$ lub $(\ref{4})$ ma dwie stałe całkowania $C_1$ i $C_2$ , które wyznaczamy z warunków brzegowych. Zależności pomiędzy siłami $T(x)$, $H(x)$ i siła w linie $S(x)$ po uwzględnieniu zależności geometrycznych (rys.1) można zapisać w postaci:
$$ \begin{equation} \begin {cases}
T(x)= H \cdot tan \varphi= H \cdot y^{’}(x) \\
S(x)= \sqrt{H^2+T^2(x)}=Hv \sqrt{1+{y^{’}}^2(x)}=H \sqrt{1+tan^2 \varphi}= \cfrac{H}{cos \varphi} \\
\end {cases} \label{6}\end{equation} $$
gdzie $\varphi$ jest lokalnym kątem nachylenia cięgna.
Krzywa łańcuchowa
Znajdziemy rozwiązanie równania różniczkowego $(\ref{4})$ dla obciążenia $q_2(x)= g = const$ ( g może być ciężarem własnym cięgna). Po wprowadzeniu zmiennej pomocniczej $u=y^{’}$ równanie to można zapisać w postaci:
$$ \begin{equation} H u^{’} =g \sqrt {1+u^2} \to \cfrac{du}{\sqrt{1+u^2}}=\cfrac{g}{H} \cdot dx \label{7} \end{equation} $$
Całką ogólną tego równania różniczkowego jest
$$ \begin{equation} ln \left ( u + \sqrt{1+u^2}\right)= \cfrac{g}{H}\cdot x +C_1 \to u+ \sqrt {1+u^2}= e^{\left( \cfrac{g}{H}x+C_1\right)} \to y^{’}+ \sqrt {1+{y^{’}}^2}= e^{ \left( \cfrac{g}{H}x+C_1\right)} \label{8} \end{equation} $$
Ponieważ $\cfrac{d (lnx)}{dx}=\cfrac{1}{x}$, wiec $(\ref{8})$ można zapisać w postaci:
$$ \begin{equation} \cfrac{1}{y^{’} + \sqrt {1+{y^{’}}^2}}=e^{- \left( \cfrac {g}{H}x+C_1\right)} \label{9} \end{equation} $$
Odejmując stronami ( $(\ref{8})$ – $(\ref{9})$ ) uzyskamy
$$ \begin{equation} 2y^{’}=e^{\left( \cfrac{g}{H}x+C_1\right)}-e^{- \left( \cfrac{g}{H}x+C_1\right)} \to y^{’}= \cfrac{1}{2} \left \{ e^{ \left( \cfrac{g}{H}x+C_1\right)}-e^{- \left( \cfrac{g}{H}x+C_1\right)} \right \} \label{10} \end{equation} $$
Rozwiązanie zagadnienia cięgna uzyskamy po przecałkowaniu równania $(\ref{10})$ w postaci:
$$ \begin{equation} y= \cfrac{H}{2g} \left \{ e^{\left( \cfrac{g}{H}x+C_1\right)}-e^{- \left( \cfrac{g}{H}x+C_1\right)} \right] \} + C_2 \label{11} \end{equation} $$
Stałe całkowania $C_1$ , $C_2$ oraz stałą $H$ (reakcję poziomą podpory) należy określać dla konkretnych warunków brzegowych.
Cięgno układa się w krzywą łańcuchową (katenoidę)
Na rys. 10 przedstawiono układ pojedynczego cięgna, które ułożyło się w idealną krzywą łąńcuchową ($\ref{1}$). Cięgno jest zawieszone w punktach A i B symetrycznie rozmieszczonych w stosunku do osi rzędnych y i obciążone jedynie ciężarem własnym q.
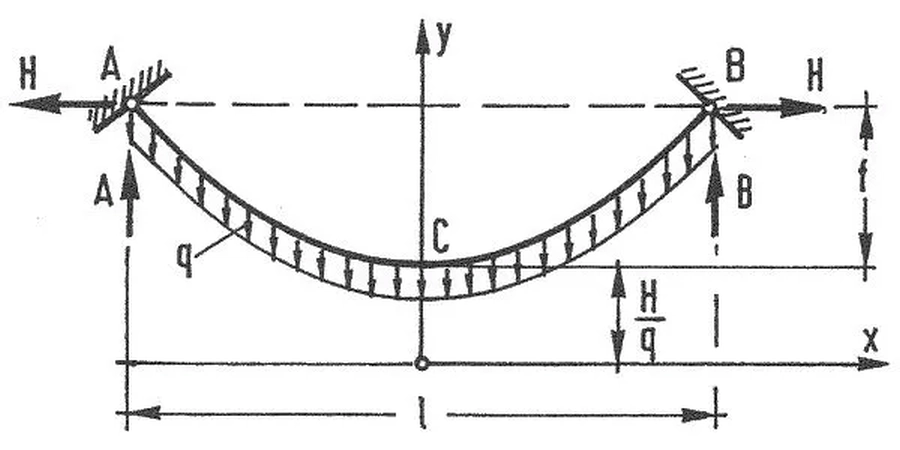
Rys.10. Cięgno układa się w krzywą łańcuchową pod ciężarem własnym [28], rozdz. 12, rys. 18
W układzie współrzędnych przyjętym zgodnie na rys. 10 – z początkiem zaczepionym poniżej najniższego punktu cięgna, tak by ten punkt miał współrzędne
$C \left (0, \cfrac{H}{g}\right )$
stałe całkowania zerują się: $C_1 = 0$ i $C_2 = 0$.
W takim układzie punkty zaczepienia cięgna mają współrzędne: $A(-\cfrac{l}{2}, f+\cfrac{H}{g})$, $B(\cfrac{l}{2}, f+\cfrac{H}{g})$, ugięcie cięgna wynosi $\delta (x)= y-(f +\cfrac{H}{g})$ , a rozwiązanie ($\ref{11}$) przyjmuje kształt krzywej łańcuchowej (katenoidy) ($\ref{12}$):
$$ \begin{equation} y= \cfrac{H}{2g} \left \{ e^{\tfrac{x}{ H/g}}+ e^{-\tfrac{x}{ H/g}} \right \} = \cfrac a cosh \cfrac{x}{a} \label{12} \end{equation} $$
z parametrem $a=\cfrac{H}{g}$ w równaniu ($\ref{1}$) i na rys. 1.
Aproksymacja krzywej łańcuchowej parabolą
W praktyce krzywą łańcuchową aproksymuje się parabolą 2-go stopnia, która jest podstawową krzywą ugięcią belki prostej i umożliwiającą stosowanie analogii belkowej.
Po rozłożeniu kosinusa hiperbolicznego w szereg potęgowy – krzywą łańcuchową ($\ref{12}$) można zapisać w postaci
$$ \begin{equation} y= \cfrac{H}{g} \left ( 1+ \cfrac{x^2}{2!(H/g)^2}+\cfrac{x^4}{4! (H/g)^4}+ …\right) \approx \cfrac{H}{g}+\cfrac{g}{2H}\cdot x^2 \label{13} \end{equation} $$
Strzałka zwisu cięgna $f$ (rys.10) wynosi:
$$ \begin{equation} f=y(\cfrac{l}{2})-\cfrac{H}{g}= \cfrac{H}{g}\left( cosh \cfrac{l/2}{H/g}-1\right) \approx \cfrac{gl^2}{8H}+ \cfrac{g^3 l^4}{384 H^3}+ \cfrac{g^5l^6}{46080 H^5}+ … \label{14} \end{equation} $$
Kąt nachylenia linii cięgna określa pochodna $y^{’}$ funkcji $(\ref{13})$:
$$ \begin{equation} \varphi =y^{’}=sinh \cfrac{x}{H/g} \approx \cfrac{x}{H/g}+ \cfrac{x^3}{3!(H/g)^3}+ … \label{15} \end{equation} $$
Po wprowadzeniu oznaczeń
$$ \begin{equation} \begin {cases}
m=\cfrac{H/g}{l/2}= \cfrac{2H}{gl} \\
n_f=\cfrac{f}{l} \\
n_L=\cfrac{L}{l} \\
\end {cases} \label{16} \end{equation} $$
otrzymamy:
$$ \begin{equation}\begin {cases}
\textrm {dla krzywej łańcuchowej} & n_f= \cfrac{m}{2}\left ( cosh \cfrac{1}{m}-1\right) \quad ; \quad n_L=m \cdot sinh \cfrac{1}{m} \\
\textrm {dla paraboli} & n_f=\cfrac{1}{4m}\quad ; \quad n_L=\cfrac{1}{2}\sqrt{1+(1/m)^2}+\cfrac{m}{2}\cdot ln \left({\cfrac{1}{m}+ \sqrt{1+(1/m)^2}} \right) \\
\end {cases} \label{17} \end{equation} $$
Na rys.11 graficznie pokazano różnice między ścisłymi zależnościami (dla krzywej łańcuchowej) i aproksymacji parabolą. Dokładność aproksymacji jest zadawalająca dla płaskich cięgien, o strzałce zwisu $f/l<0,12$, co odpowiada współczynnikowi obciążeń $m=\cfrac{2H}{gl} > 2$.
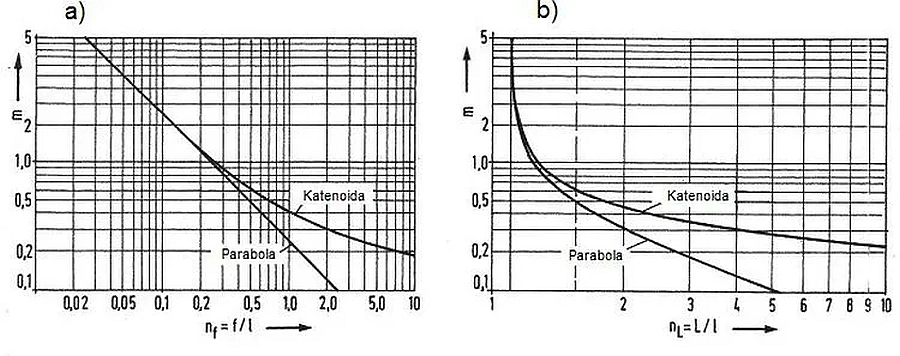
Rys.11. Dokładność aproksymacji linii cięgna parabolą. Współczynnik obciążeń $m$ w funkcji: a) $n_f$, b) $n_L$ [28]– rozdz. 12, rys. 19
Siły i długość cięgna
Po podstawieniu wyrażenia na linię cięgna ($\ref{14}$) do ($\ref{6}$a,b) , można uzyskać następujące wyrażenia na siły w cięgnie:
$$ \begin{equation} \label{18} \begin {cases}
T(x)=H \cdot sinh \cfrac{x}{a} \\
S(x)=H \cdot cosh \cfrac{x}{a}= g \cdot y\\
\end {cases} \end{equation} $$
gdzie: $a=\cfrac{H}{g}$ ($\ref{1}$)
W sposób ścisły uzyskano ważny rezultat: Siła w cięgnie S(x) jest równa iloczynowi obciążenia liniowego cięgna ( np. ciężaru własnego) oraz rzędnej linii cięgna w danym punkcie po jego długości.
Zależność ($\ref{18}$b) jest prawdziwa wyłącznie w układzie współrzędnych z rys. 10.
Siła działająca na podporę wynosi $S(l/2)= q \cdot (H/g+f)$, a reakcja pionowa podpory $ A= T(l/2)= H \cdot sinh \cfrac{l/2}{H/g} = g \cfrac{l}{2}$
Długość cięgna po rozciągnięciu uzyskana z zależności ($\ref{5}$) wynosi :
$L= \int \limits_{-l/2}^{l/2} \sqrt{1+{y^{’}}^2}dx =\int \limits_{-l/2}^{l/2} \sqrt{1+sinh^2 \cfrac{x}{H/g}} dx= \int \limits_{-l/2}^{l/2} \sqrt{cosh \cfrac{x}{H/g}} dx= \cfrac{H}{g}\cdot sinh \cfrac{x}{H/g} |_{-l/2}^{l/2}$
czyli
$$ \begin{equation} L=2 \cfrac {H}{g} \cdot sinh \cfrac{l/2}{H/g} \approx l \cdot \left ( 1+\cfrac{g^2l^2}{24h^2}+\cfrac {g^4 l^4}{1920 H^4} \right) \label{19} \end{equation} $$
Podpory na różnych wysokościach
W przypadku cięgna pokazanego na rys. 12, zawieszonego na podporach o różnych wysokościach, ułoży się ono również wg krzywej łańcuchowej ($\ref{12}$), przy czym punkt symetrii jest przeniesiony do punktu B’, oddalonego o $a$ od osi rzędnych y.
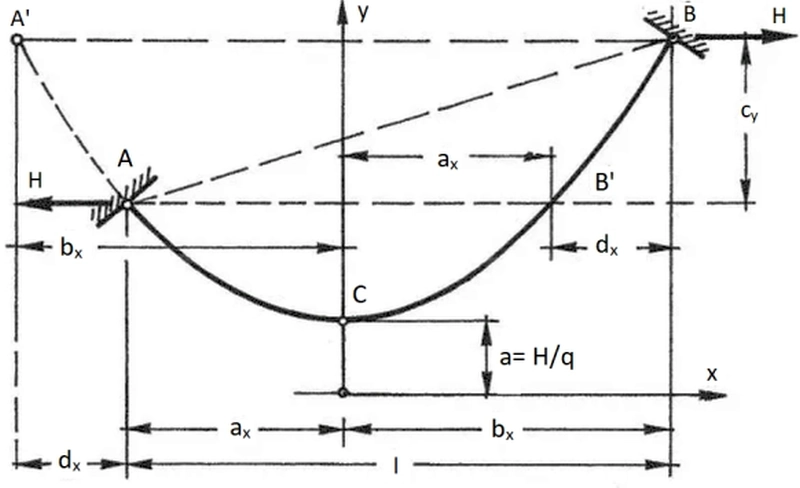
Rys.12 Pojedyncze cięgno zawieszone na różnych wysokościach [28]– rozdz. 12, rys. 20
Różnica wysokości podpór $c$ wynosi
$$ \begin{equation} c= a \cdot \left( cosh \cfrac{b_x}{a}- cosh \cfrac{a_x}{a}\right)\label{20} \end{equation} $$
gdzie $a_x$ i $b_x$ są odległościami poziomymi podpór od osi $y$. Zachodzą związki geometryczne: $l=2 a_x+d_x \to a_x=\cfrac{l-d_x}{2}$ ; $l=2 b_x – d_x \to b_x=\cfrac{l+d_x}{2}$.
Długość krzywej , wyznaczona z $(\ref{19})$ w granicach [a,b], wynosi
$$ \begin{equation} L=L_{AC}+L_{CB}= a \cdot \left ( sinh \cfrac{a_x}{a}+ sinh \cfrac{b_x}{a}\right) = \sqrt {c_y^2 + \left ( 2 \cdot c_y \cdot a \cdot sinh \cfrac{l}{2 a}\right)^2 } \label{21} \end{equation} $$
Obowiązuje zależność $S=g \cdot y$, a reakcje pionowe podpór wynoszą:
$$ \begin{equation} \label{22} \begin {cases}
A=H \cdot sinh \cfrac{a_x}{a} \\
B=H \cdot sinh \cfrac{b_x}{a}\\
\end {cases} \end{equation} $$
$a$ wg ($\ref{1}$)
Styczna do linii cięgna w punkcie $C$ jest równoległa do cięciwy krzywej (rys 13a).
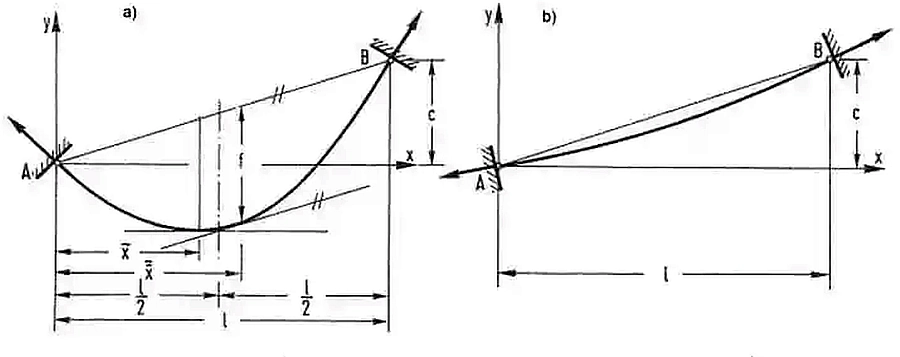
Rys. 13 Własności liny zawieszonej na różnych wysokościach: a) z dużym zwisem, b) z małym zwisem [28] – rozdz. 12, rys. 21
Ponieważ punkt $C$ leży w odległości $a$ od podpory, to $y^{’}= sinh \cfrac{ \overline x-a_x}{a}=0 \to \overline x=a$.
W celu wyznaczenia odległości $\bar {\bar x} $ należy skorzystać z równania $ y^{’}= sinh \cfrac{\bar {\bar x}-a_x}{a}=\cfrac{c}{l}$. Po wyznaczeniu $\bar {\bar x} $ można obliczyć strzałkę ugięcia z formuły
$$ \begin{equation} f= \cfrac{c_y}{l}\cdot \bar{\bar x}- a \left ( cosh \cfrac{\bar {\bar x}- a_x}{a}-cosh \cfrac{a_x}{a}\right) \label{23} \end{equation} $$
Równanie stanu napiętej liny
Podstawowe równanie stanu
Ze względu na silne nieliniowości geometryczne w przypadku cięgien nie obowiązuje zasada superpozycji.
Rozpatrzmy cięgna w dwóch stanach, pokazanych na rys. 16. W pierwszym cięgno o długości $l$, obciążone jest liniowo $q_1$ i temperaturą $t_1$, wskutek czego wystąpi rozciąg $H_1$ i strzałka zwisu $f_1$. Siła w cięgnie $S_1 \approx H_1$. W drugim stanie tego samego cięgna odpowiednie wielkości oznaczono indeksem „2”. Składową obciążenia $q$ jest ciężar własny $g$.
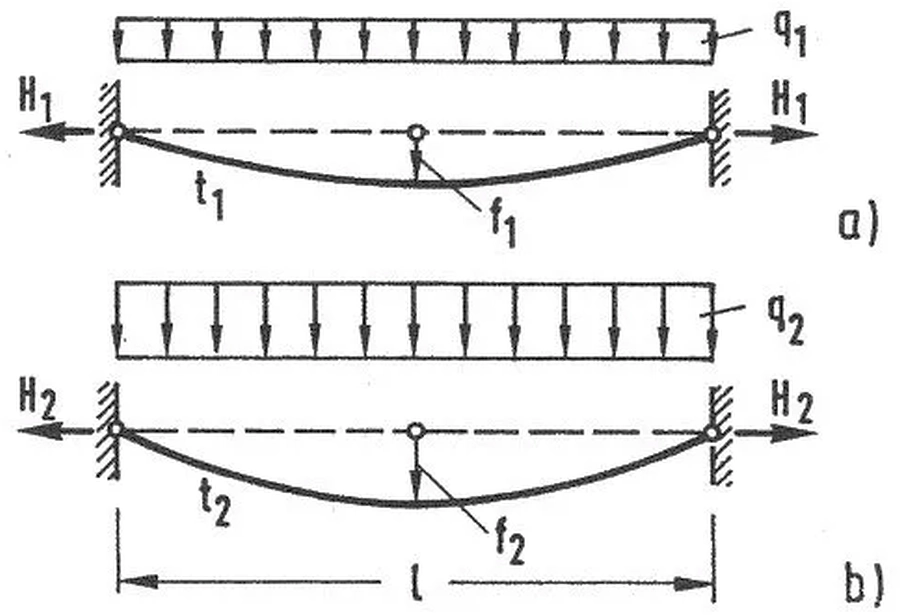
Rys.16. Dwa stany obciążenia cięgna: a) stan $q_1, t_1$, b) stan $q_2, t_2$ [28] – rozdz. 12, rys. 35
Przy aproksymacji linii cięgna parabolą otrzymamy naciągi:
$$ \begin{equation} \label{24} \begin {cases}
H_1= \cfrac{q_1 l^2}{8f_1} \approx S_1 \\
H_2= \cfrac{q_2 l^2}{8f_2} \approx S_2\\
\end {cases} \end{equation} $$
a także długości napiętego cięgna
$$ \begin{equation} \label{25} \begin {cases}
L_1= l \cdot \left \{ 1+\cfrac{8}{3} \cdot \left ( \cfrac{f_1}{l} \right)^2 \right \} = l \cdot \left \{ 1 + \left( \cfrac{q_1^2}{24 \cdot H_1}\right)^2 \right \} \\
L_2= l \cdot \left \{ 1+\cfrac{8}{3} \cdot \left ( \cfrac{f_2}{l} \right)^2 \right \} = l \cdot \left \{ 1 + \left( \cfrac{q_2^2}{24 \cdot H_2}\right)^2 \right \} \\
\end {cases} \end{equation} $$
Różnica długości cięgna w obu stanach wynosi:
$$ \begin{equation} \Delta L= L_2-L-1= \cfrac{l^3}{28}\cdot \left \{ (\cfrac{q_2}{H_2})^2- (\cfrac{q_1}{H_1})^2\right \} = \cfrac{l^3}{28}\left \{ (\cfrac{\gamma_2}{\sigma_2})^2- (\cfrac{\gamma_1}{\sigma_1})^2\right \} \label{26} \end{equation} $$
gdzie wprowadzono oznaczenia:
$$ \begin{equation} \label{27} \begin {cases}
\gamma=\cfrac{q}{A_m}\\
\sigma=\cfrac{H}{A_m}=\cfrac{S}{A_m} \\
A_m \quad \textrm{ – pole przekroju metalicznego (stalowego) rdzenia cięgna}\\
\end {cases} \end{equation} $$
Z drugiej strony na podstawie prawa fizycznego Hooka mamy :
$$ \begin{equation} \Delta L = \left \{ \cfrac{\sigma_2-\sigma_1}{E}+\alpha_t \cdot (t_2-t_1)\right \} \label{28} \end{equation} $$
Po przekształceniach równanie $ (\ref{26})=(\ref{27})$ można zapisać w postaci
$$ \begin{equation} \left( \cfrac{\sigma_2}{\sigma_1}\right)^3 =\left \{ \cfrac{E \gamma_1^2 l^2}{24 \sigma_1^3}+\cfrac{E}{\sigma_1} \cdot \alpha_t\cdot (t_2-t_1)-1\right \} \cdot \left( \cfrac{\sigma_2}{\sigma_1}\right)^2 -\cfrac{E\gamma_2^2 l^2}{24 \sigma_1^3} = 0 \label{29} \end{equation} $$
Równanie $(\ref{29})$ nazywane jest równaniem stanu naciągniętego cięgna. Równanie jest nieliniowe – stopnia trzeciego względem $\sigma_2$. Może być rozwiązane dowolną metodą, przy czym w obliczeniach inżynierskich najczęściej stosuje się podejście iteracyjne.
Równanie stanu dla obciążenia rzutowanego
W przypadku, gdy na cięgno działają obciążenie grawitacyjne liczone na rzut pokrycia, to do równania stanu (36) należy wprowadzić modyfikację. Rozpatrzmy cięgno o długości w rzucie $l$ , wysokości $h$, rozpięte pod kątem $\alpha$ i zwisem $\overline f $ . Długość początkowa cięgna wynosi
$$ \begin{equation} s=\sqrt{l^2+h^2} \label{30} \end{equation} $$
Obciążenie $q$ (rys.17a) należy rozłożyć na:
$$ \begin{equation} \overline q = q \cdot cos\alpha \quad oraz \quad \overline{\overline q}= q\cdot sin \alpha \label{31} \end{equation} $$
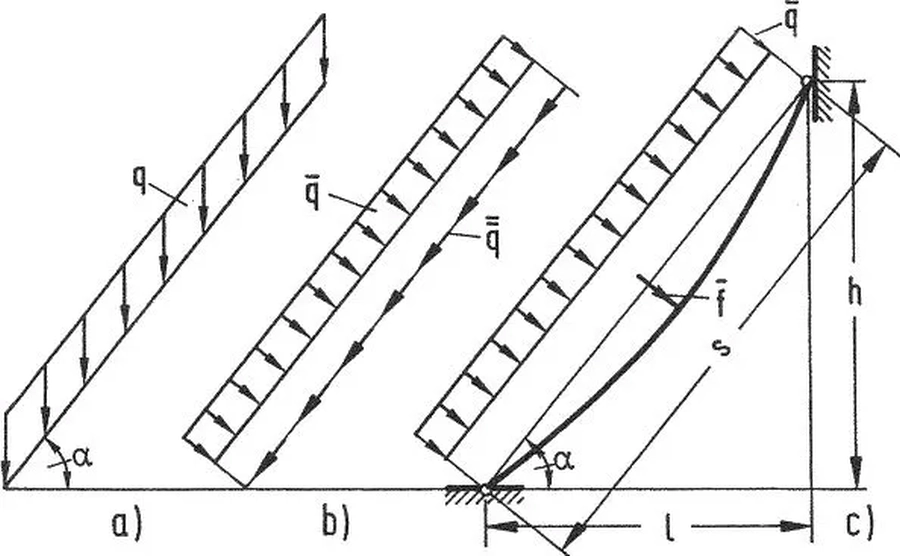
Rys.17. Obciążenie rzutowane cięgna [28] – rozdz. 12, rys. 37
Zmodyfikowane równanie stanu ($\ref{28}$) uzyskuje się po zastąpieniu długości $ l$ przez $s$ oraz $\gamma$ przez $\overline \gamma$:
$$ \begin{equation} \overline \gamma_1 = \cfrac{\overline q_1}{A_m} \quad ; \quad \overline \gamma_2 = \cfrac{\overline q_2}{A_m} \label{32} \end{equation} $$
W rezultacie uzyskujemy zmodyfikowane równanie stanu cięgna
$$ \begin{equation} \left( \cfrac{\sigma_2}{\sigma_1}\right)^3=\left \{ \cfrac{E \overline \gamma_1^2 s^2}{24 \sigma_1^3}+\cfrac{E}{\sigma_1} \cdot \alpha_t\cdot (t_2 – t_1)-1\right \} \cdot \left( \cfrac{\sigma_2}{\sigma_1}\right)^2 -\cfrac{E\overline \gamma_2^2 s^2}{24 \sigma_1^3}=0 \label{33} \end{equation} $$
Cięgno rozpięte na konstrukcji odkształcalnej
W przypadku rozpięcia cięgna na konstrukcji odkształcalnej można wyznaczyć zastępczą stałą sprężystości poziomej konstrukcji i rozpatrzyć schemat ze sprężystą podporą o stałęj $C$, pokazany na rys.10. Należy przy tym rozpatrzyć różnice dwóch stanów obciążeń: podczas montażu $q_1$ (rys.18 a) , w którym powstaje naciąg $H_1$ i stanu eksploatacyjnego $q_2$ (rys.10b), w którym powstaje naciąg $H_2$.
$$ \begin{equation} \Delta l =\cfrac{H_2-H_1}{C}=\cfrac{A_m}{C}(\sigma_2 – \sigma_1) \label{34} \end{equation} $$
W równaniu $(\ref{32} b)$ należy zamienić $l$ na $l-\Delta l$. W rezultacie wystąpią też stosowne zmiany w równaniu stanu $(\ref{33})$.
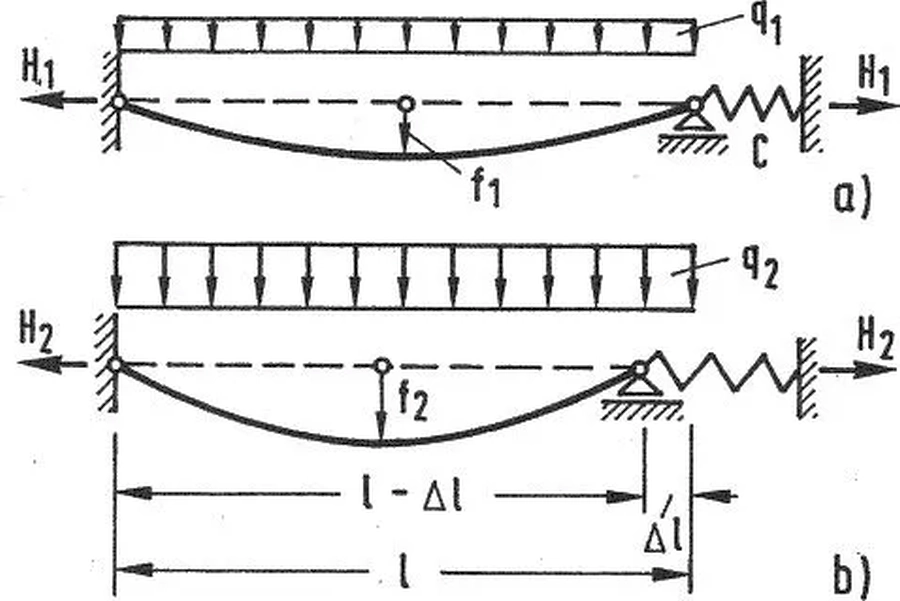
Rys. 18 Dwa stany cięgna rozpiętego na sprężystej konstrukcji [28]– rozdz. 12, rys. 36
Wielokąt trasy pod obciążeniami skupionymi
W przypadku obciążenia cięgna siłami skupionymi linię cięgna można wyznaczyć iteracyjnie z wielokąta trasy cięgna ( rys. 14). W pierwszym przybliżeniu zakładamy nieodkształcalność osiową cięgna $EA=\infty $.
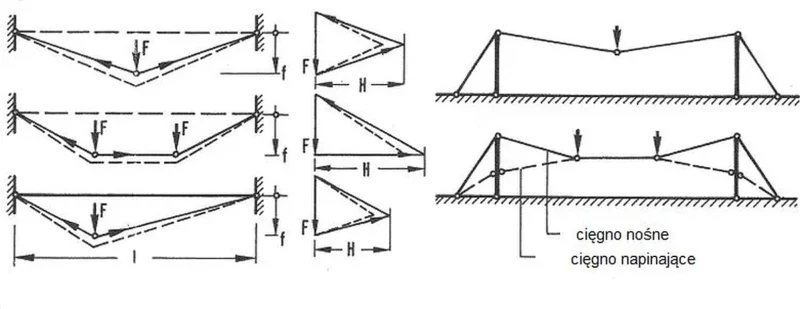
Rys.14 Wielokąt siłtras w cięgnie :a) schemat obciążeń, b) kierunki tras, c) układ cięgien [28] – rozdz. 12, rys. 22
Procedurę iteracyjną w prostym przypadku tok postępowania naszkicowano na rys. 15. W pierwszym przybliżeniu rozwiązania iteracyjnego przyjmuje się, że siła pozioma $H$ oraz siła w cięgnie $S$ wynoszą
$$ \begin{equation} H=\cfrac{Fl}{4f} \quad ; \quad S=\cfrac{F}{2 sin \alpha} \label{35} \end{equation} $$
Rys.15 Szkic do wyznaczanie tras cięgien pod obciążeniem skupionym [28] – rozdz. 12, rys. 23
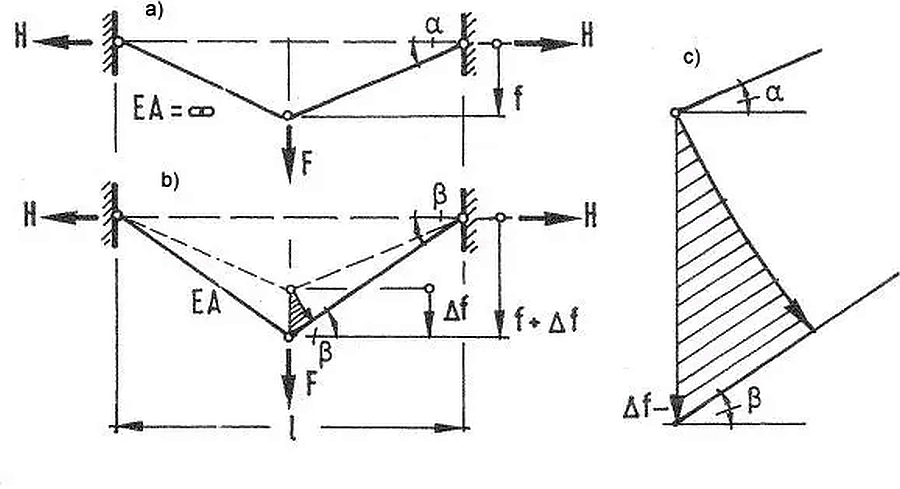
Dla przypadku $EA=\infty$ mamy następujące zależności geometryczne:
$$ \begin{equation} tan \beta= \cfrac {f+\Delta f}{l/2} \to f+ \Delta f= \cfrac{l}{2}tan \beta \quad ; \quad sin \beta= \cfrac {f+\Delta f}{\left( 1+\cfrac{S}{EA} \right)\cdot \sqrt{f^2 +(l/2)^2}} \label{36} \end{equation} $$
W wyrażeniu $(\ref{36})$ nie uwzględniono sprężystej odkształcalności cięgna. W takim razie $(\ref{35})$ należy poprawić w drugiej iteracji $(\ref{37})$
$$ \begin{equation} H=\cfrac{Fl}{4(f+ \Delta f)}=\cfrac{F}{2 sin \alpha} \quad ; \quad S=\cfrac{F}{2 sin \beta}=\cfrac {\left( 1+\cfrac{S}{EA} \right)\cdot \sqrt{f^2 +(l/2)^2}}{2(f+ \Delta f)} \cdot F \label{37} \end{equation} $$
Pomiędzy stanem odkształconym, a pierwotnym wystąpiło następujące przemieszczenie:
$$ \begin{equation} \sqrt{(f+\Delta f)^2+(l/2)^2}- \sqrt{f^2+(l/2)^2}= \cfrac{S}{EA}\cdot \sqrt{f^2+(l/2)^2} \label{38} \end{equation} $$
W równaniach ($\ref{37}$) i ($\ref{39}$) występują dwie nieznane wielkości $S$ i $\Delta f$, które można wyznaczyć z układu równań($\ref{31}$) przekształconych z zapisu wyżej:
$$ \begin{equation} \label{39} 2 \cdot \cfrac{S}{F}\cdot (f+\Delta f) – \left( 1+ \cfrac{S}{EA}\right)\cdot \sqrt{f^2 +(l/2)^2}=0 ; \quad
\sqrt{(f+\Delta f)^2 =(l/2)^2}-\left( 1 + \cfrac{S}{EA}\right)\cdot \sqrt{f^2 + (l/2)^2}=0 \end{equation} $$
Układ równań ($\ref{32}$) można sprowadzić do jednego równania nieliniowego do wyznaczania $S$:
$$ \begin{equation} \label{40} \sqrt{ \left ( \cfrac{F}{2S}\cdot \left ( 1+ \cfrac{S}{EA}\right ) \cdot \sqrt{ f^2 +(l/2)^2}\right)^2 +(l/2)^2}- \left ( 1+ \cfrac{S}{EA}\right ) \cdot \sqrt{f^2 +(l/2)^2}=0 \end{equation} $$
Teraz można wyznaczyć $\Delta f $ z zależności
$$ \begin{equation} \label{41} \Delta f = \cfrac{F}{2S}\cdot \left ( 1+ \cfrac{S}{EA}\right ) \cdot \sqrt{f^2 +(l/2)^2}-f \end{equation} $$
Analiza statyczna i dynamiczna układów cięgnowych
Analizę statyczną i dynamiczną układów cięgien prowadzi się numerycznie ze wspomaganiem zaawansowanych programów obliczeniowych na przykład wymienionych w rozdziale.
W przypadku współpracy układu cięgien z przekryciem membranowym prowadzi się jednoczesną analizę układu cięgna-membrany. W przypadku ułożenia na cięgnach pokrycia, nie współpracującego z konstrukcją linową można prowadzić odrębną analizę. Nie jest jednak zalecane projektowanie przekrycia/pokrycia nie współpracującego z układem i nie jest też w aktualnej praktyce realizowane.
Wymiarowanie konstrukcji cięgnowych
Warunek trwałości drutów, lin i splotek
Liny muszą być zabezpieczone przed korozją. Przykłady zabezpieczenia antykorozyjnego lin podano na rys. 15.
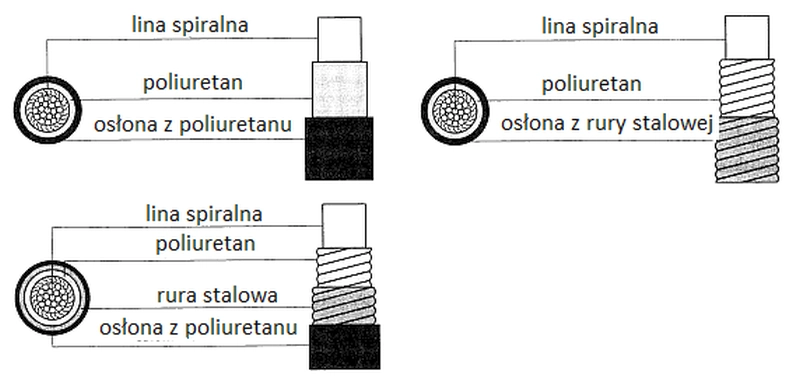
Rys.15. Przykłady zabezpieczenia antykoroyzjnego liny [29]
Cięgna grupy B i C przynależne do klas ekspozycji 2, 4, i 5 wg tab.3., wymagają następującej ochrony:
- Poszczególne druty powinny być zabezpieczone przed korozją poprzez ocynkowanie lub pokrycie stopami cynku.
Powłoki drutów okrągłych z cynku lub jego stopów w cięgnach grupy B powinny spełniać wymagania klasy A wg [30], a do drutów zetowych stosuje się wymagania klasy A wg {{PN-EN 10264-3:2012, Drut stalowy i wyroby z drutu -Drut stalowy na liny -Część 3: Drut okrągły i kształtowy ze stali niestopowej do pracy w trudnych warunkach obciążenia}}, przy czym do tych drutów zazwyczaj stosuje się grubszą powłokę galwaniczną 300 g/m2, aby zrekompensować względny ubytek grubości w ostrych narożach, a powłoka ze stopu Zn95Al5 stanowi znacznie lepszą ochronę niż powłoka galwaniczna tej samej grubości i dlatego druty okrągłe i zetowe można pokrywać powłoką o podstawowej gramaturze Zn95Al5.
W przypadku cięgien grupy C dla powłok ochronnych należy spełnić wymagania [20]. - Wnętrze liny powinno być zabezpieczone przed przenikaniem wilgoci.
Wszystkie przestrzenie wewnątrz cięgna grupy B, wypełnia się aktywnym lub pasywnym wypełniaczem, który nie powinien ulegać przemieszczeniom wskutek działania wody, ciepła lub drgań. Wypełniaczem aktywnym są oleje poliuretanowe z pyłem cynkowym. Wypełniaczem pasywnym może być trwale sprężysto-plastyczny wosk lub żywica wodorowa z płatkami aluminium. Wypełniacze wewnętrzne wprowadzone podczas wytwarzania cięgien są narażone na wyciskanie podczas obciążania, co wymaga innych zabezpieczeń w stosownym czasie. Przy doborze wewnętrznego wypełnienia wymagana jest jego określona zgodność z pozostałymi środkami ochrony. - Powierzchnia zewnętrzna powinna by zabezpieczona przed korozją.
Po zakończeniu montażu cięgien grupy B, stosuje się dodatkowe środki ochrony powierzchni zewnętrznych cięgien grupy B, w celu likwidacji uszkodzeń i uzupełnieniu warstwą cynku. Takie zabezpieczenie może stanowić osłona polietylenowa lub farba wysoko pigmentowana cynkiem, przy czym minimalna grubość osłony polietylenu wynosi min[d/15, 3 mm], gdzie d- średnica liny. Zabezpieczenia malarskie obejmuje: powłokę poliuretanową z pyłem cynkowym jako podkład 2×50 μm + powłokę poliuretanową z miką żelazną jako wykończenie 2×125 μm.
Cięgna grupy B ze stali nierdzewnej oraz nierdzewne wykończenia bez dodatkowych zabezpieczeń powinny odpowiadać wymaganej klasie odporności korozyjnej. Cięgna grupy C wymagają dwóch niezależnych powłok antykorozyjnych z odpowiednią warstwą izolacyjną. Odpowiednie zabezpieczenia w miejscach zacisków, siodeł i zakotwień powinny zapobiec napływowi wody deszczowej. Połączenia konstrukcji cięgnowych powinny być uszczelnione.
Odcinki końcowe cięgien grupy C na ogół chroni się za pomocą rurowej osłony stalowej lub polietylenowej, przy czym przestrzeń między cięgnem a wnętrzem osłony powinna być wypełniona odpowiednim wypełniaczem antykorozyjnym lub zaprawą cementową. Alternatywnie stosuje się bezpośrednio natłoczoną osłonę poliuretanową lub zabezpieczenia poszczególnych splotek lub cięgien powłokami epoksydowymi.
Osłona cięgien grupy C powinna być szczelna w strefie zakotwienia, złącza osłony projektuje się tak, by nie pękały przy jej rozciąganiu. Przy zaciskach i zakotwieniach stosuje się dodatkowe zabezpieczenia, aby zapobiec penetracji wody. Pustki wypełnia się całkowicie materiałem hydrofobowym, który nie oddziałuje niekorzystnie na cięgno. Alternatywnie stosuje się ochronę cięgna przez cyrkulację suchego powietrza wewnątrz osłony. Materiał hydrofobowy stanowią wypełniacze miękkie, jak: smar, wosk, miękka żywica lub wypełniacze twarde, jak cement. Skuteczność wypełniaczy powinna być potwierdzona badaniami.
Wymagania dotyczące transportu i składowania i montażu zawiera Załącznik B [12].
Ochrona cięgien głównych w mostach wiszących wymaga specjalnej troski. Po uzyskaniu wymaganego przekroju, cięgno jest owijane ściśle przylegającą miękką taśmą ocynkowaną w otoczce odpowiedniej pasty, niezbędnej do całkowitego wypełnienia pustki między powierzchnią drutów zewnętrznych cięgna, a taśmą ochronną. Po usunięciu nadmiaru pasty z wierzchu taśmy, powłoka cynkowa jest czyszczona, a następnie malowana. Specjalnych zabiegów w mostach wiszących wymagają strefy zakotwienia cięgien, z których taśma ochronna jest usuwana. Powszechnym sposobem jest ochrona przed dostępem wilgoci do przestrzeni wokół drutów.
Warunki nośności i użytkowalności – ogólne zasady
W analizie konstrukcji cięgnowych rozpatruje się stany graniczne nośności ULS (SGN), w których obciążenie osiowe nie może przekroczyć obliczeniowej nośności przy rozciąganiu oraz stan graniczny użytkowalności SLS (SGU), w którym naprężenia i odkształcenia nie powinny przekroczyć wartości granicznych, a także kryterium zmęczenia, w którym zakresy zmienności naprężeń, wywołane zmiennością obciążeń osiowych oraz drganiami od wiatru i deszczu nie powinny przekraczać wartości granicznych. Ze względu na wymagania trwałości, kryterium użytkowalności często jest decydujące.
Elementy wyposażenia cięgien prefabrykowanych, takie jak siodła i zaciski, projektuje się również ze względu na stany graniczne ULS i SLS, przy czym elementy te dobiera się „na nośność liny”, przyjmując do obliczeń oddziaływania, odpowiadające nośności liny – sile zrywającej lub gwarantowanej wytrzymałości. Zmęczenie sprawdza się wg [31]. Oddziaływania zmęczeniowe na liny są uzależnione od promienia krzywizny siodła lub strefy zakotwienia.
Rozpatrzeć należy dwie sytuacje obliczeniowe:
- Sytuację przejściową podczas budowy, czyli procesu, obejmującego: formowanie, montaż i wstępny naciąg cięgien, w której zalecane jest stosowanie współczynnika obciążeń stałych γG=1,10 w sytuacji krótkotrwałej (rzędu kilku godzin) przy instalowaniu pierwszego cięgna i γG=1,20 przy instalowaniu kolejnych cięgien (γG=1,00 w przypadku korzystnych efektów oddziaływań).
Sytuacja, w której stan graniczny jest zdeterminowany przez obciążenie „G+P” (jednoczesne działanie obciążenia stałego G i wstępnego naciągu cięgna „P”), wymaga zastosowania współczynnika obciążeń γP, przy czym zaleca się stosowanie γP=1.Technologia budowy powinna być tak zaprojektowana, aby można było uzyskać:- wymaganą geometrię konstrukcji,
- odpowiedni stan naprężenia od oddziaływań stałych, pozwalający spełnić kryteria SGN i SGU we wszystkich miarodajnych sytuacjach projektowych i eksploatacyjnych.
Wykonawca i obsługujący go technolog powinien w szczególności prawidłowo zastosować środki kontrolne, umożliwiające pomiar kształtu, pochylenia, deformacje, częstotliwości, kolejność i sposób zadawania sił, tak by miarodajne były wartości charakterystyczne obciążeń stałych, wymuszonych deformacji i innych obciążeń. Nie należy dopuszczać do przypadkowego zadziałania sił lub awaryjnego (losowego) przyjęcia kształtu przez montowaną konstrukcję.
- Sytuację trwałą podczas eksploatacji, w której zależnie od stanu granicznego ULS, czy SLS, czy zmęczenia, współczynniki częściowe γm=γR należy różnicować, uwzględniając ostrość warunków podczas badań atestacyjnych oraz przyjęte środki przeciwdziałania efektom zgięciowym. Oddziaływanie stałe „G+P” odpowiada nominalnej geometrii konstrukcji.
W analizie układów zarówno w fazie budowy jak i eksploatacji uwzględnia się nieliniowe efekty oddziaływań, wynikające z odkształceń konstrukcji (silne nieliniowości geometryczne). Uwzględnia się deformacje (zmiany geometrii) wywołane zwisem cięgien, ich skróceniem bądź wydłużeniem w tym w fazie eksploatacji wydłużeniem od pełzania. Efekt zwisu można uwzględniać w ten sposób, że dla poszczególnych cięgien lub ich segmentów przyjmować zastępczy moduł sprężystości Et określony wzorem (10) – wzór 5.1 [12]:
$$ \begin{equation} E_t= \cfrac {E}{l+ \cfrac {w^2 \ \ l^2 \ \ E} {12 \cdot \sigma^3}} \label{42}\end{equation} $$
gdzie: $E$ [MPa] moduł sprężystości cięgna , $w$ [MPa/mm] – ciężar jednostkowy (tab. 4), $ \sigma$ [MPa] – naprężenia w cięgnie, przy czym w przypadku sytuacji typowych w fazie eksploatacji $\sigma=\sigma_{„G+P”}$, $l$ [mm] – rozpiętość pozioma cięgna.
Całkowitą długość cięgna oraz wymiary związane z rozmieszczaniem siodeł i zacisków oznacza się dla nieokreślonego naciągu, przy czym wymagane są dodatkowe oznaczenia kontrolne, umożliwiające późniejsze dokładne sprawdzenie wymiarów po zakończeniu montażu. Tolerancje wykonania bierze się pod uwagę po przeciągnięciu oraz po cyklicznych próbach obciążenia i odciążenia. Konstrukcje wrażliwe na odchyłki wymiarów wyposaża się w odpowiednie urządzenia regulujące.
Analizy konstrukcji cięgnowych i cięgnowo-membranowych należy prowadzić wg teorii II-giego lub III-ciego rzędu przy odpowiednich założeniach dotyczących imperfekcji układu, to znaczy należy uwzględnić wpływ przemieszczeń i odkształceń na siły i naprężenia konstrukcji obarczonej imperfekcjami.
W celu wyznaczenia efektów oddziaływań zmiennych przyjmuje się początkową geometrię konstrukcji, odpowiadającą stanowi obciążeń $”G+P”$ przy określonej temperaturze T0. Nieliniowe odpowiedzi wyznacza się dla konstrukcji o nominalnej geometrii w temperaturze oddziaływania T0, poddanej kombinacji oddziaływań obliczeniowych $\gamma_G \cdot „(G+P)”+\gamma_Q \cdot Q_{k1} +\gamma_Q \cdot \Psi_2 Q_{k2}$
Nośność cięgna
Układy z cięgnami prętowymi (grupa A), ze względu na stan graniczny nośności, wymiaruje się standardowo zgodnie z [32] i [14], zależnie od rodzaju stali.
Warunek nośności dla prętów sprężających oraz cięgien grup B i C zgodnie z (6.1) [12] ma postać:
$$ \begin{equation} \cfrac {F_{Ed}}{F_{Rd}}\leq 1 \label{43}\end{equation} $$
gdzie: $F_{Ed}$ – wartość obliczeniowa siły podłużnej w elemencie, $F_{Rd}$ – wartość obliczeniowa nośności przy rozciąganiu.
Wg (6.2) [12]:
$$ \begin{equation} F_{Rd}=\ min \left[ \cfrac {F_{uk}}{1,5 \gamma_R} \, ; \, \cfrac {F_k}{\gamma_R} \right] \label{44}\end{equation} $$
gdzie: $F_{uk}$ – wartość charakterystyczna siły zrywającej, $ F_k$ – wartość charakterystyczna umownej nośności przy rozciąganiu wg tab. 7, $\gamma_R$ – współczynnik częściowy, zależny od tego, czy stosuje się odpowiednie środki na końcach cięgien w celu redukcji momentów zginających od skręcania cięgna: zalecana wartość $\gamma_R=0,9 $ , jeśli środków takich nie zastosowano i $\gamma_R=1,0 $, jeśli środki zastosowano.
Tab.7. Umowna nośność cięgien [12]– tab. 6.1.
Sprawdzenia w stosunku do $F_k$ opierają się na założeniu, że cięgno pozostaje w warunkach oddziaływań obliczeniowych. W przypadku cięgien (np. lin zamkniętych), dla których $ F_k \ge \frac {F_{uk}}{1,5}$ sprawdzenie to nie jest wymagane. Zgodnie z [33] wartości eksperymentalne $F_{uke}$ i $F_{ke}$ uzyskane z badań przy odbiorze elementów, powinny przewyższać wartości charakterystyczne: $ F_{uke} >F_{uk}, F_{ke} >F_k$.
W przypadku cięgien grupy B siła zrywająca wynosi wg (6.4) [12]
$$ \begin{equation} F_{uk}=F_{min} \cdot k_e \label{45}\end{equation} $$
gdzie minimalna siłę zrywajacą $F_{min}$ wyznacza się zgodnie z (6.5) wg [12]:
$$ \begin{equation} F_{min}= \cfrac {K \cdot d^2 \cdot R_r}{1000}\ \ kN \label{46}\end{equation} $$
gdzie Rr– wytrzymałość liny w MPa, ke – współczynnik straty wskutek zakotwienia według tab.8.
W przypadku prętów sprężających lub cięgien grupy C wartość charakterystyczna siły zrywającej wynosi (15) – (6.3) wg [12]:
$$ \begin{equation} F_{uk}=A_m \cdot f_{uk} \label{47}\end{equation} $$
gdzie fuk – wartość charakterystyczna wytrzymałości na rozciąganie prętów, drutów lub splotek według odpowiedniej normy wyrobu, $A_m$ – pole przekroju metalowego cięgna.
Wartości K, d, Rr dla lin są określone w [13].
Tab.8. Współczynnik straty ke [12]-tab. 6.3.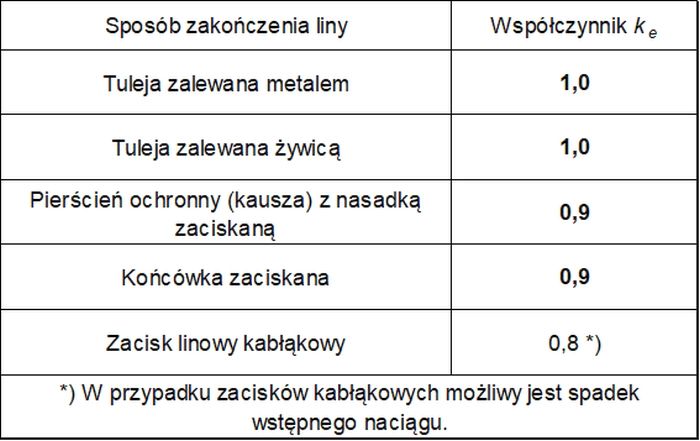
Siodła i zaciski
Jeśli parametry geometryczne siodła spełniają warunki podane na rys. 16 , a ponadto promień krzywizny siodła r1 ≥[30d; 400∅], gdzie: ∅- średnica drutu, d- średnica cięgna, d’– szerokość strefy styku; przy tym, że wartość r1 może być zredukowana do 20d, jeśli podłoże liny na szerokości równej co najmniej 60% średnicy jest pokryte warstwą miękkiego metalu lub natrysku cynkowego o grubości co najmniej 1 mm, to naprężenia wywołane zakrzywieniem drutów można pominąć w obliczeniach.
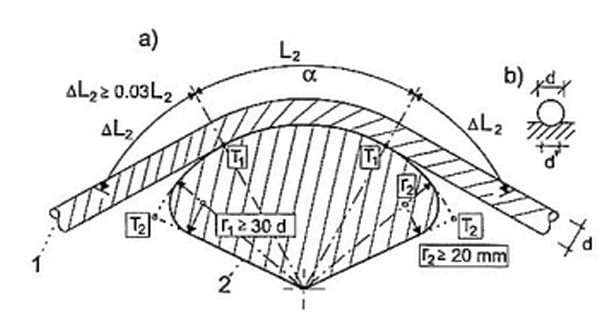
Rys.16 Lina w siodle: 1-splotka-lina, 2- siodło, $L_11$ -długość teoretycznie zakrzywionego odcinka splotu/liny między punktami $T_1$ w warunkach najniekorzystniejszej kombinacji obciążeń charakterystycznych z uwzględnieniem zwisu, $\Delta L_2$ – potencjalny przyrost długości $L_2$ z jednej strony siodła [12]– rys. 6.1
Położenie punktów T1 i T2 (rys.16) wyznacza się dla odpowiednich przypadków obciążenia, uwzględniając ruchy łożysk i przemieszczenia cięgien.
W przypadku lin jednozwitych stosowanie siodeł o mniejszym promieniu wymaga uzasadnienia eksperymentalnego.
Aby zapobiec poślizgowi cięgien sprawdza się warunek (16) – (6.6) wg [12]:
$$ \begin{equation} max \frac {F_{Ed1}}{F_{Ed2}} \leq e^{\frac{\mu\alpha}{\gamma_{M,fr}}} \label{48}\end{equation} $$
gdzie: $F_{Ed1}$, $F_{Ed2}$ – obliczeniowe wartości odpowiednio większej i mniejszej siły w cięgnie po obu stronach siodła, μ – współczynnik tarcia, α – kąt w radianach, określający strefę styku, $\gamma_{M,fr}$ -współczynnik częściowy związany z oporem tarcia. Zaleca się przyjmować $\gamma_{M,fr}=1,65$.
Jeśli warunek (16) nie jest spełniony, to jest niezbędne zastosowanie zacisków wywierających dodatkowy docisk radialny siłą $F_r$, tak by spełniony był warunek (6.7) [12]:
$$ \begin{equation} \cfrac {F_{Ed1} – {\frac {k \cdot F_r \cdot \mu}{\gamma_{M,fr}}}}{F_{Ed2}} \leq e^{\frac{\mu\alpha}{\gamma_{M,fr}}} \label{49}\end{equation} $$
gdzie: $k$ – współczynnik przy w pełni efektywnym tarciu między zaciskiem a bruzdami siodła.
Gdy siła $F_r$ nie przekracza nośności cięgna na docisk (p. niżej), przyjmuje się $k=2,0$, a w pozostałych przypadkach $k=1,0$.
Ustalając siłę $F_r$ w zależności od śrub sprężających, rozpatruje się następujące wpływy i okoliczności:
- długotrwale pełzanie,
- redukcję średnicy przy wzroście rozciągania,
- sprasowanie lub owalizację cięgna,
- spadek siły sprężającej w zaciskach śrubowych wywołany obciążeniem zewnętrznym,
- różnicę temperatur.
Warunek nośności cięgna na docisk qEd od siły oddziaływania zacisku $F_r$ ma postać (6.8) [12] :
$$ \begin{equation} \cfrac {q_{Ed}}{q_{Rd}}\leq 1 \label{50}\end{equation} $$
gdzie:
$q_{Ed}= \frac{F_r}{d’L_2}$, przy czym:
$0,6 d \le d’ \le d$ , ($d’$ wg rys.16b), $q_{Rd} = \frac {q_{Rk}}{\gamma_{M,bed}}$,
$\gamma_{M,bed}$ – współczynnik częściowy. Przy przyjęciu podanych wartości granicznych $q_{Rk}$ ze współczynnikiem $\gamma_{M,bed} =1,00$ spadek nośności cięgna na zerwanie nie przekracza 3%.
Naprężenie $q_{Rk}$ jest graniczną wartością docisku, którą wyznacza się eksperymentalnie. Przy braku szczegółowych badań wartości graniczne docisku można przyjąć następująco:
- jeśli zastosowano stalowe zaciski i siodła;
$q_{Rk}=40$ MPa dla liny zamkniętej,
$q_{Rk}=25$ MPa dla liny splotowej jednozwitej, - jeśli zastosowano zaciski na poduszkach i siodłach
$q_{Rk}=100$ MPa dla liny zamkniętej,
$q_{Rk}=60$ MPa dla liny splotowej jednozwitej.
Zaciski na poduszkach powinny mieć warstwę miękkiego metalu lub natrysku cynkowego o grubości co najmniej 1 mm.
Siodła wymiaruje się na charakterystyczną siłę zrywającą $F_{uk}$ pomnożoną przez współczynnik $k$. Zaleca się przyjmować $k=1,1$.
Jeśli zacisk ma przenosić siłę podłużną na cięgno, a części (rys.17) nie są wzajemnie zaklinowane, to w celu wyeliminowania poślizgu należy spełnić warunek (6.9) [12] :
$$ \begin{equation} F_{Ed \parallel }\leq \cfrac {(F_{Ed \perp} + F_r)} {\gamma_{M,fr}} \label{51}\end{equation} $$
gdzie:
$F_{Ed \parallel }$ – składowa obliczeniowa siły zewnętrznej równoległa do cięgna, $F_{Ed \perp}$ – składowa obliczeniowa siły zewnętrznej prostopadła do cięgna, $F_r$ – radialna siła zacisku, $\mu$ – współczynnik tarcia, $\gamma_{M,fr}=1,65$ – współczynnik częściowy dla oporu tarcia.
Siła radialna może ulec zmniejszeniu lub zwieszeniu na skutek zmiany sposobu przenoszenia siły zewnętrznej przez zacisk.
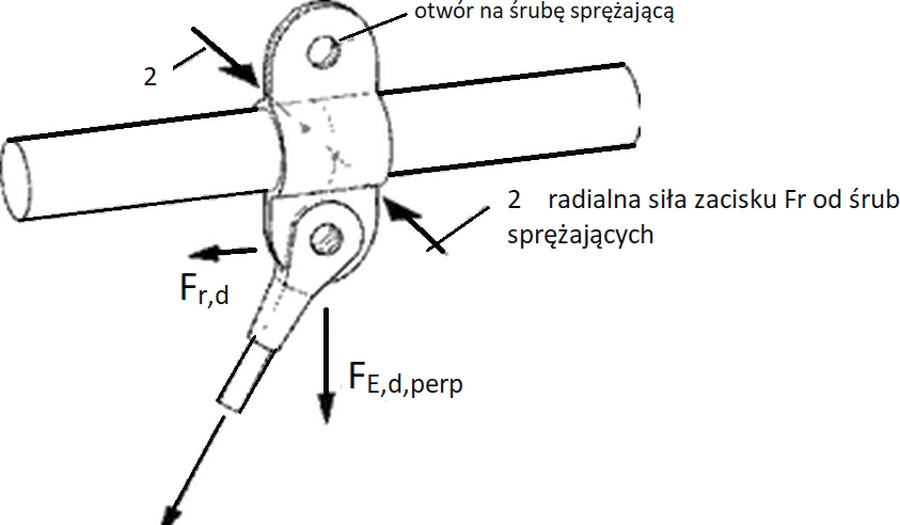
Rys.17. Docisk w zacisku [12]-rys. 6.2
Nośność na docisk od siły $F_{Ed \perp} +F_r$ lub $F_{Ed \parallel }$ sprawdza się w sposób analogiczny jak podano wyżej.
Zaciski oraz ich środki złączne, jak np. połączenia wieszaków z cięgnem głównym, wymiaruje się na umowną siłę obliczeniową o wartości $1,15\cdot F_k$, gdzie $F_k$ jest charakterystyczną nośnością cięgna dołączanego. Stosowanie wartości $F_k$ oznacza wymiarowanie na pełną nośność.
Użytkowalność konstrukcji cięgnowej
Rozpatruje się następujące kryteria użytkowalności:
- kryteria deformacji lub drgań,
- kryteria stanu sprężystego.
Ograniczenie deformacji lub drgań przekłada się na wymagania odnoszące się do sztywności układu konstrukcyjnego, wstępnego naciągu cięgien oraz nośności zacisków na poślizg. Ograniczenia związane z zachowaniem stanu sprężystego dotyczą maksymalnej i minimalnej wartości naprężeń od kombinacji obciążeń właściwych ze względu na stany graniczne użytkowalności.
Ograniczenie naprężeń wprowadza się po to, by:
- zapewnić sprężystą odpowiedź układu w odpowiednich sytuacjach obliczeniowych odnoszących się do fazy budowy i eksploatacji,
- ograniczyć odkształcenia, które w przeciwnym razie mogłyby obniżyć skuteczność zabezpieczeń antykorozyjnych (np. przez pękanie osłon, twardych wypełniaczy, rozszczelnienie złączy, itd.), a także wpłynąć niekorzystnie na zmęczenie,
- przy sprawdzaniu stanów granicznych ULS można było w analizie przyjmować liniową odpowiedź układu.
Ograniczenie naprężeń określa się w stosunku do wytrzymałości na zerwanie:
$$ \begin{equation} \sigma_{uk}= \cfrac {F_{uk}}{A_m}\label{52}\end{equation} $$
gdzie: $F_{uk}$, $A_m $ – jak wyżej.
Naprężenie graniczne $f_{const}$ wyznacza się ze wzoru:
$$ \begin{equation} f_{const}= \cfrac {\sigma_{uk}}{1,5 \gamma_R \cdot \gamma_F}= \cfrac {0,66 \sigma_{uk}} {\gamma_R\cdot\gamma_F}\label{53}\end{equation} $$
przy czym $\gamma_R \cdot \gamma_F=1,0\cdot 1,10 =1,10$ w przypadku sytuacji krótkotrwałych, $\gamma_R \cdot \gamma_F=1,0\cdot 1,20=1,20$ w przypadku sytuacji długotrwałych.
Zaleca się ograniczać naprężenia $f_{const}$ w fazie budowy do wartości:
$f_{const}= 0,60 \sigma_{uk}$ – kilka godzin po zainstalowaniu pierwszych cięgien,
$f_{const}= 0,55 \sigma_{uk}$ – po zainstalowaniu pozostałych cięgien.
Naprężenie graniczne $f_{SLS}$ wyznacza się analogicznie do $f_{const}$ze wzoru (21), ale z innymi współczynikami bezpieczestwa, a mianowicie:
$\gamma_R \cdot \gamma_F=0,90\cdot 1,48=1,33$ , gdy uwzględnia się naprężenia od zginania i $\gamma_R \cdot \gamma_F=1,0\cdot 1,48=1,48$ , gdy nie uwzględnia się naprężenia od zginania.
W badaniach przyjmuje się $f_{SLS}=0,45 \sigma_{uk}$.
W fazie eksploatacji naprężenia graniczne $f_{SLS}$ uzależnia się od warunków obciążenia, w następujący sposób:
$f_{SLS}=0,50 \sigma_{uk}$ – przy oddziaływaniu zmęczeniowym z uwzględnieniem zginania,
$f_{SLS}=0,45 \sigma_{uk}$ -przy oddziaływaniu zmęczeniowym bez uwzględnienia zginania.
Drgania cięgien
W przypadku cięgien konstrukcji wolno stojących (np. odciągów) ze względów bezpieczeństwa rozpatruje się drgania wywołane wiatrem w fazie budowy oraz w fazie eksploatacji.
Siły aerodynamicznego oddziaływania wiatru na cięgna ujawniają się jako zjawiska:
- uderzenia przy turbulentnym przepływie powietrza,
- wzbudzenie wirowe (zawietrzne wiry Karmana),
- galopowanie (drgania samowzbudne),
- galopowanie wskutek interakcji z innymi cięgnami,
- łączne oddziaływanie wiatru i deszczu,
Galopowanie nie następuje w przypadku cięgien o przekroju okrągłym z powodu symetrii. Jednak zjawisko może wystąpić wskutek zmiany kształtu spowodowanej osadzaniem się warstw lodu lub pyłu. Siły towarzyszące galopowaniu i łącznemu działaniu wiatru i deszczu są funkcją ruchu cięgna i efektem niestateczności aerodynamicznej w postaci drgań o dużej amplitudzie po przekroczeniu krytycznej prędkości wiatru. Ponieważ modele dynamicznego wzbudzenia drgań nie są jeszcze wystarczająco dokładne z punktu widzenia analizy niezawodności, należy stosować się odpowiednie środki ograniczające drgania.
Drgania cięgien mogą być także wywołane oddziaływaniami dynamicznymi na inne części konstrukcji (jak np. dźwigary, pylony). Zjawisko to jest często określane jako „wzbudzenie parametryczne”, które odpowiada za drgania o dużej amplitudzie, gdy nakładają się drgania własne odciągów i konstrukcji.
Konstrukcje podparte cięgnami montuje się z uwagi na nadmierne drgania wywołane wiatrem i deszczem, stosując oględziny lub inne metody, umożliwiające dokładne wyznaczenie postaci, amplitud i częstości drgań.
Projekt i wykonawstwo konstrukcji cięgnowych powinny uwzględniać odpowiednie środki ograniczające drgania podczas lub po zakończeniu montażu. Do takich środków zalicza się:
- modyfikację powierzchni cięgien (aerodynamiczny kształt),
- urządzenia tłumiące,
- cięgna stabilizujące (np. odciągi pionowe z odpowiednimi połączeniami)
Ryzyko drgań zwiększa się wraz ze zwiększaniem długości odciągu. Odciągi krótkie (o długości mniejszej niż 70 do 80 m) na ogół nie stwarzają takiego ryzyka, chyba że mamy do czynienia z konstrukcjami niezbyt stabilnymi (wskutek kształtu lub podatnego pomostu), które są narażone na rezonans typu parametrycznego.
W przypadku cięgien długich, o długości większej od 80 m, projekt powinien przewidywać instalację tłumików o krytycznym stosunku tłumienia przekraczającym 0,5%. Tłumiki rozmieszcza się przy tych cięgnach, których zakotwienia nie wykazują znacznych przemieszczeń.
Ocenę ryzyka rezonansu parametrycznego przeprowadza się w toku szczegółowej analizy postaci niestateczności konstrukcji i odciągów, rozpatrując częstotliwości kątowe i przemieszczenia zakotwień dla każdej postaci drgań.
Stosuje się odpowiednie środki, aby zapobiec nakładaniu się częstotliwości, tj. sytuacjom, w których częstotliwość wzbudzenia cięgien zawiera się w przedziale 20% częstotliwości drgań własnych konstrukcji (pierwszej lub drugiej częstotliwości). W razie konieczności stosuje się cięgna stabilizujące, powodujące przesunięcie kątowych częstotliwości drgań poszczególnych odciągów.
Ze względu na komfort użytkowników i bezpieczeństwo, amplitudę drgań odciągów wyznacza się za pomocą kryterium odpowiedzi konstrukcji, zgodnie z którym przy umiarkowanej prędkości wiatru 15 m/s amplituda drgań nie powinna przekroczyć wartości L/500, gdzie L-długość odciągu.
Generalnie drganiom cięgien od wiatru i deszczu należy zapobiegać przez odpowiednie rozwiązania projektowe. Wchodzi w grę zastosowanie odciągów z lin teksturowanych.
Zmęczenie konstrukcji cięgnowych
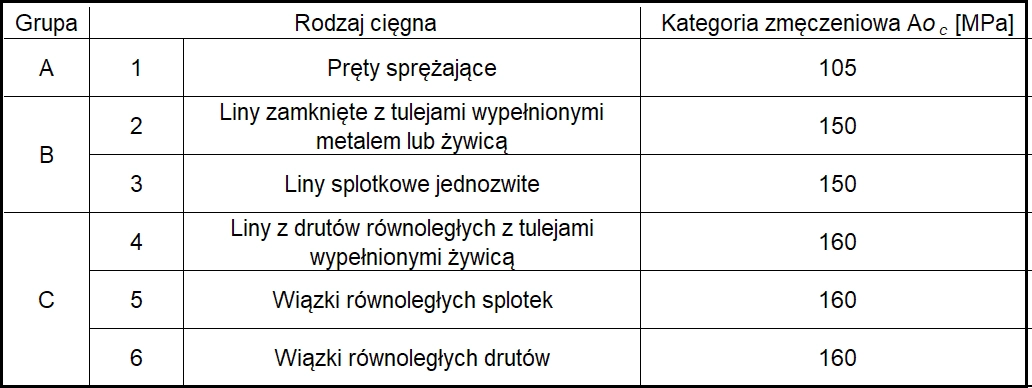
Trwałość zmęczeniowa cięgien w klasie 3, 4 lub 5 określa się na podstawie oddziaływań zmęczeniowych wg [31] oraz odpowiednich kategorii zmęczeniowych szczegółów konstrukcyjnych.
Zniszczenie zmęczeniowe układów cięgnowych na ogół następuje w miejscach zakotwień, siodeł lub zacisków. Miarodajne kategorie zmęczeniowe tych szczegółów konstrukcyjnych powinno się określać na podstawie badań odwzorowujących rzeczywiste konfiguracje, występujące w praktyce, a także wpływ zginania i oddziaływań poprzecznych. Ocenę wyników badań przeprowadza się wg Załącznika D [12].
Przy braku odpowiednich badań krzywe wytrzymałości zmęczeniowej i kategorie zmęczeniowe można ustalać odpowiednio według rys. 18 i tab. 9.
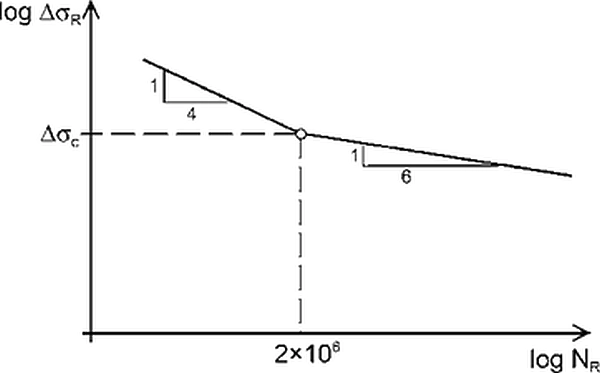
Rys.18 Krzywa wytrzymałości zmęczeniowej dla cięgna [12]-rys. 9.1
Tab.9. Kategorie zmęczeniowe Δσc, odpowiadające wytrzymałości zmęczeniowej [31] – tab.9.1
Konstrukcje membranowe
Powłoki membranowe najczęściej są rozpinane na konstrukcji cięgnowej scharakteryowanje wczewśniej , ale mogą być również rozpięte na sztywnych ramach lub ścianach, masztach, belkach, kratownicach itd.
Wprowadzenie
W ostatnich latach wraz z postępem w technologii produkcji tkanin technicznych trwałych, ekonomicznych i o dużej wytrzymałości wzrosło znaczenie i stosowanie przekryć membranowych w licznych obszarach architektury i inżynierii jako przekrycia na: stadionach, amfiteatrach, lotniskach, centrach handlowych, halach wystawowych, widowiskowych, parkach rozrywki, halach magazynowych i produkcyjnych, parkingach, stacjach benzynowych, restauracjach, zadaszeniach przystanków, wejść do hoteli czy biurowców, kortach tenisowych, basenach itd. Tego typu materiały konstrukcyjne mogą tworzyć również elementy fasad. Technologie oparte na materiałach tekstylnych stały się stałym elementem nowoczesnej architektury przede wszystkim obiektów sportowych i rekreacyjnych.
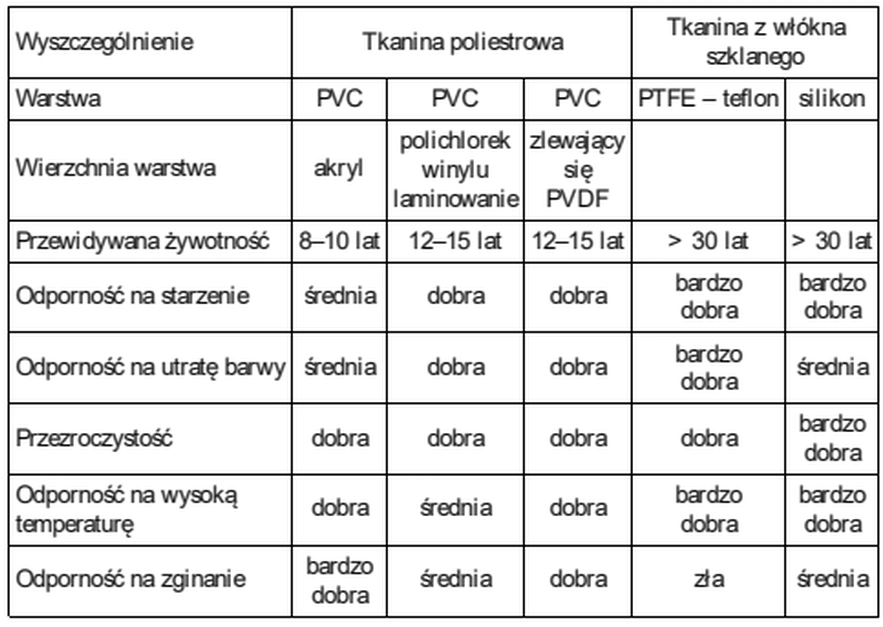
Właściwości tkanin technicznych stosowanych w architekturze tekstylnej umożliwiają projektowanie zadaszeń o różnorodnych formach architektonicznych, m.in. parabolicznych, stożkowych, łukowych, symetrycznych i niesymetrycznych, żagle, siodła czy stożki, i in. Tworzy się z nich także struktury sferyczne i pneumatyczne. Tkanina architektoniczna jest wytrzymałym i trwałym materiałem budowlanym wykorzystywanym do zadaszenia zarówno stałych, jak i tymczasowych obiektów. W tab. 10 zestawiono za pracą ( Buczkowski W. (Red), Budownictwo ogólne, tom 4, Konstrukcje budynków, rozdz. 5.2, Zagubień A, rozdz. 5.2), KOnstrukcje tekstylne))
Tab.10 Własności tkanin technicznych ( Buczkowski W. (red.), Budownictwo ogólne, tom 4, Konstrukcje budynków, rozdz. 5.2, Zagubień A, rozdz. 5.2, Konstrukcje tekstylne))
Najbardziej ekonomicznym materiałem membranowym jest PVC/PVDF – idealne rozwiązanie zarówno dla stałych jak i tymczasowych struktur. Tkanina pokryta warstwą PVC/PVDF ma wiele zalet: jest miękka, elastyczna i lekka jednocześnie mając bardzo dużą wytrzymałość na rozciąganie. W szerokim zakresie zmian temperatury i wilgotności pozostaje stała wymiarowo, a specjalny proces powlekania warstwą ochronną zapobiega tworzeniu się pleśni, plam i smug. Przekrycia membranowe mogą przybierać różne formy o dowolnych kształtach i wymiarach:
Tkaniny techniczne posiadają izolacyjność cieplną, dającą częściową i ochronę cieplną i ograniczenie strat ciepła w kierunku na zewnątrz obiektu.
Pojedyncza warstwa membrany Valmex FR 1000 o wadze około 1050 g/m² ma współczynniki izolacyjności cieplnej U =5,7 W/m²K , natomiast dwuwarstwowa konstrukcja zadaszenia membranowego ze szczeliną powietrzną szerokości 200 mm ma U= ok. 2,7 W/m²K. Zadaszenia membranowe umożliwiają osiągnięcie jeszcze lepszych wartości izolacyjności cieplnej poprzez dodanie kolejnych warstw materiału konstrukcyjnego lub izolacyjnego. Trzeba wziąć jednak pod uwagę, że im więcej będzie warstw membrany w konstrukcji zadaszenia, tym mniej światła będzie ono przepuszczać.
Specjalne rodzaj tkanin technicznych charakteryzuje odporności ogniowej (np. Valmex® Fr.), a przede wszystkim tkaniny są tak zaprojektowane, że nie powstają płonące krople materiału i materiał jest NRO.
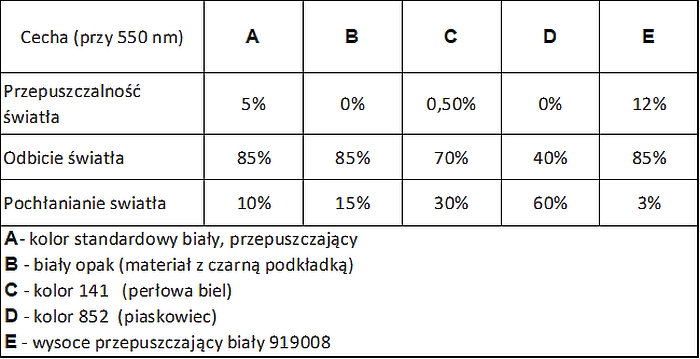
W zależności od koloru tkaniny mamy różne parametry świetlne tkanin podane w tab. 11 na przykładzie tkanin Valmex.
Tab.11. Parametry świetlne tkani technicznych. przykład Valmex [34]
Analizy statyczne przekryć (cięgnowo-) membranowych
Powłoki tekstylne są znamienne tym, że nieliniowości geometryczne są jeszcze silniejsze niż w konstrukcjach cięgnowych. Przyjmuje się, że właściwą teorią do analizy membran tekstylnych jest teoria III rzędu, polegająca na rozwinięciu ścisłej macierzy sztywności do 3-go wyrazu szeregu Taylora. Z tego powodu ważne jest posługiwanie się właściwym oprogramowaniem, umożliwiającym taką analizę. Współcześnie jest dostępnych kilka programów a tego zakresu, a między innymi:
- EASY Technet GMBH [35],
- RFEM i RSTAB do analizy i wymiarowania kabli i membran. zmodułem RF-FORM-FINDING do znajdowania kształtu przekrycia dla RFEM [36],
- SOFISTIK [37].
Przykłady rachunkowe
Przykład 1 [ Iteracyjne rozwiązanie cięgna pod siła skupioną ]
Przykład pochodzi z pracy Petersen (2013) [28]– str 844, (rys.7).
Przykład w opracowaniu
Dla cięgna o przekroju $A=0,5 cm^2 $, wykonanego ze stali o module Younga $E=16 000 kN/cm^2 \to EA=8000 kN $. w chemacie pokazanym na rys.
W tabeli rys. 7b) wyznaczyć siłę rozciągającą ciegno.
podano wyniki obliczeń iteracyjnych przeprowadzonych zgodnie z podanymi wyżej zależnościami. Na rys. 7c) pokazano wykres porównawczy siły we cięgnie wywołanej siła skupioną $F=$ 0 do 20 kN dla iteracji pierwszej ($EA= \infty$) i dla drugiej ($EA=8000 kN$). W przykładzie pokazano, że błąd oszacowania zwiększa się wraz ze zwiększaniem się wartości siły $F$ i wynosi 15% dla $F=20 kN $, to znaczy jest istotny i obliczenia nieliniowe są wymagane.
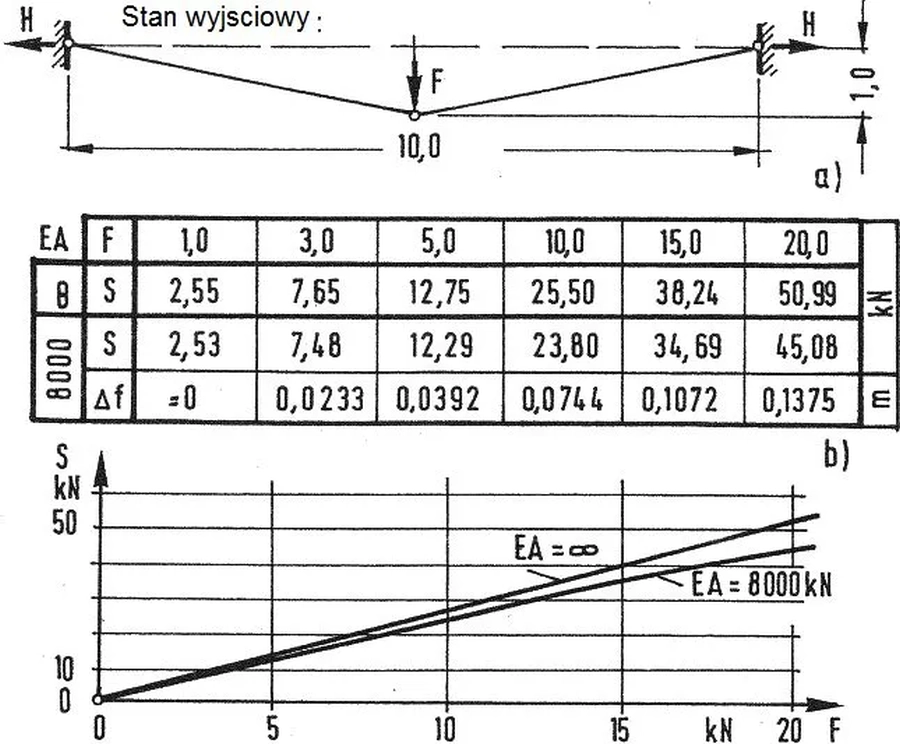
Rys. P1-1 Przykład rachunkowy wyznaczenia tras cięgna pod obciążeniem skupionym: a) schemat, b) tabela iteracyjna, c) wykres porównawczy [28] – rozdz. 12, rys. 24
W przypadkach bardziej złożonych obciążeń , a także dla siatek cięgnowych zalecane jest stosowanie specjalistycznego oprogramowania, np Sofistic AG.
Załączniki
Załącznik 1 [Równanie stanu cięgna ]
W załączniku przestawiono eleganckie wyprowadzenie równania stanu cięgna wg pracy pracy Chodor (2016) [38]. W załączniku stosuje się inne oznaczenia od wprowadzonych w rozdziale inne w rozdziale Równanie stanu napiętej liny,
Statykę rozciągliwego cięgna o cięciwie ukośnej rozpatrzmy na schemacie, pokazanym na rys.Z1-1. Cięgno o długości $L$ rozpięto pomiędzy podporami na różnych wysokościach. Po odkształceniem cięgno przechodzi do stanu oznaczonego apostrofem (’) i rozciąga do długości $L’$.
Rys. Z1-1 Schemat statyczny pochyłego cięgna [38] – zmodyfikowane
I równowagi (Naviera),
II geometryczne (Cauchy’ego) i
III fizyczne.
Warunek równowagi I
Warunek idealnej wiotkości cięgna zapiszemy po prostu w postaci zerowania się momentu zginającego w dowolnym punkcie cięgna:
$$ \begin{equation} M(x) =H \cdot w(x) \quad \to \quad w(x) =\cfrac{M(x)}{H} \label{54}\end{equation} $$
gdzie:
$H =Nˑ\cdot cos \alpha$ – składowa pozioma początkowego naciągu $N$,
$\alpha$ – kat nachylenia cięgna w konfiguracji początkowej (przed odkształceniem),
$ w(x)$ – zwis cięgna w punkcie o współrzędnej $x$,
$M(x)$ – moment zginający obliczony jak dla zastępczej belki podpartej tak jak cięgno na podporach w odległości $L$
Różniczkowanie funkcji ($\ref{54}$) daje wyrażenie na nachylenie stycznej do odkształconego cięgna w punkcie $x$:
$$ \begin{equation} w'(x) =\cfrac{Q}{H}\label{55}\end{equation} $$
gdzie $Q=dM(x)/dx$ jest siłą poprzeczną w belce zastępczej.
Równanie geometryczne II
Rozpatrzmy odcinek (P-Q) cięgna o długości dx, który po odkształceniu przyjął pozycję (P’-Q’) i ma długość dx’. Przyrost długości cięgna Δ(dx) wynosi
$$ \begin{equation} \Delta (dx) = dx’-dx = dx \cdot \sqrt{(dx)^2 + ( \cfrac{dw}{dx} \cdot dx )^2} = dx \left ( \sqrt{1+ (w’)^2}-1 \right) \label{56}\end{equation} $$
Rozwijając pierwiastek w szereg Maclaurina, otrzymujemy
$$ \begin{equation} \Delta (dx) = dx \cdot \left [ 1+1/2 w’^2- 1/4 w’^4 + … \right ] \approx \cfrac{1}{2} [ w'(x)[ ^2 \label{57}\end{equation} $$
W rezultacie ze ścisłego nieliniowego warunku geometrycznego ($\ref{56}$) otrzymaliśmy aproksymację II rzędu wydłużenia cięgna $\Delta L, które po uwzględnieniu ($\ref{55}$) możemy zapisać w postaci:
$$ \begin{equation} \Delta L = \int \limits_0^{L_x} dx = \cfrac{1}{2 H^2 } \int \limits_0^{L_x} Q^2 dx \label{58}\end{equation} $$
III Równanie fizyczne możemy zapisać w postaci
Cięgno może być poddane pływom mechanicznym – obciążeniu q(x), wywołującym naciąg N oraz działaniu temperatury $\Delta T= T’-T, gdzie 'T jest temperaturą cięgna podczas montażu, a E’ w rozpatrywanym stanie
Równania fizyczne dla obu czynników można zapisać w formuł na wysłużenie od poszczególnych czynników:
- od siły N z prawa Hooka
$$ \begin{equation} \Delta L_N = \cfrac{N \ cdot L}{EA_m}$ \label{59A}\end{equation} $$
- od przyrostu temperatury $\Delta T$ z prawa rozszerzalności termicznej
$$ \begin{equation} \Delta L_T = \alpha_t \cdot \Delta T \cdot L \label{59B}\end{equation} $$
gdzie: $\alpha_t – współczynnik rozszerzalności termicznej cięgna ; $A_m$ – pole przekroju metalowego; E –moduł Younga cięgna wg rozdziału Cięgna oraz katalogów producentów lin.
Całkowite wydłużenie cięgna jest sumą ($\ref{59A}$) +($\ref{59B}$):
$$ \begin{equation} \Delta L = \Delta L_N + \Delta L_T \label{59}\end{equation} $$
Rozwiązania układu równań ($\ref{55}$) + ($\ref{58}$)+ ($\ref{59}$) możemy dokonać dowolną metodą, przy czym najczęściej ten układ równań sprowadza się do jednego równania wyższego rzędu.
Drogą eliminacji można uzyskać y jedno równania trzeciego rzędu ze względu na N: z warunku ($\rsf{55}$) bierzemy definicję $H=Nˑ\cdot cos \alpha$, podstawiamy do ($\ref{58}$), porównujemy z ($\ref{59}$), obustronnie mnożymy przez $S/N^2$ i w rezultacie uzyskamy równanie stanu cięgna w postaci ($\ref{60}$):
$$ \begin{equation} \cfrac{N^3}{EA_m} +N^2 \cdot \alpha_t \cdot \Delta T = \cfrac{1}{2 S cos ^2 \alpha } \cdot \int \limits_0^{L_x} \label{60}\end{equation} $$
Równanie ($\ref{60}$) jest najprostszym równaniem nachylonego cięgna nierozciągliwego. Jeśli jest znana długość przygotowanego na warsztacie cięgna $L_c$, to można obliczyć wymagany naciąg $N$ dla dowolnego obciążenia $q(x)$ i kąta nachylenia cięciwy cięgna, a następnie z ($\ref{55}$) można wyznaczyć rzędne osi cięgna $y=w(x)+xˑ\cdot tg\alpha$ po zwisie, a dla $x=L_x/2$ strzałkę zwisu.
W przypadku szczególnym dla $q(x)=q=const$ ( w tym dla q=g = ciężaru własnego cięgna) i dla poziomego cięgna (\alpha =0) z ($\ref{60}$) otrzymamy:
$$ \begin{equation} \cfrac{N^3}{EA_m} +N^2 \cdot \alpha_t \cdot \Delta T = \cfrac{q^2 L_x^3}{24 S} \cdot \int \limits_0^{L_x} \label{61}\end{equation} $$
Dla innych rozkładów $q(x)$ i odpowiadającej siły poprzecznej w belce swobodnie podpartej $Q(x)$ całkę ∫Q2 możemy obliczyć w dowolny sposób , w tym numerycznie.
Równania ($\ref{60}$) i ($\ref{61}$) są równaniami algebraicznymi 3-go stopnia ze względu na N i dla znanej długości cięgna S można je prosto rozwiązać dowolną metodą, a ręcznie najprościej metodą półodwrotną (zgadywania), polegającą na założeniu rozwiązania aż do wymaganej zgodności układu: równania równowagi, warunku geometrycznego i równania fizycznego.
Zadawalający obraz uzyskamy w procedurze iteracyjnej poprzez poprawianie stanu w konfiguracji odkształconej. W istocie w podobny sposób przebiega projektowanie złożonych siatek cięgien ze wspomaganiem komputerowym na przykład za pomocą programu [37].
Literatura
- Tofil J. (2010), Rozwój współczesnych przekryć o konstrukcji cięgnowej. Czasopismo Techniczne. Architektura, R. 107(z. 7-A/2), 381–386
- Kurzawa Z. (2011), Stalowe konstrukcje prętowe. Cz. II. Struktury przestrzenne, przekrycia cięgnowe, maszty i wieże. Wydawnictwo Politechniki Poznańskiej, Poznań
- Wikipedia, (2015), Krzywa łańcuchowa, [ https://pl.wikipedia.org/wiki/Krzywa_%C5%82a%C5%84cuchowa ]
- Kordos M. (2006). Kształt wiszącego łańcucha, [ https://en.wikipedia.org/w/index.php?title=Millennium_Dome&oldid=695420335 ]
- Daniel Pęcak (2009), Wyprowadzenie wzoru na krzywą łańcuchową, (2009), [ https://pl.wikipedia.org/w/index.php?title=Krzywa_%C5%82a%C5%84cuchowa&oldid=43873094 ]
- Wikipedia, (2015), Krzywa łańcuchowa, [ https://pl.wikipedia.org/w/index.php?title=Krzywa_%C5%82a%C5%84cuchowa&oldid=43873094 ]
- K2 Engineering, Kowal A. (2015). K2 Engineering- Projektowanie – Doradztwo- Konstrukcje Membranowe, [ http://www.k2se.com/realizations?locale=pl ]
- K2 Engineering, Kowal A. (2015). K2 Engineering- Projektowanie – Doradztwo- Konstrukcje Membranowe, [ http://www.k2se.com/realizations?locale=pl ]
- Wikipedia, (2015), O2 Arena (Londyn), [ https://pl.wikipedia.org/w/index.php?title=O2_Arena_(Londyn)&oldid=44019495 ]
- ArchiExpo, (2015), Metal frame supported tensile structure. – DBS Mont, [https://img.archiexpo.com/images_ae/photo-g/87104-15512631.webp]
- Butler System, (2015), Butler Structural System. [ http://www.bluescopesteel.com.au/files/dmfile/ButlerStructuralSystem.pdf ]
- PN-EN 1993-1-11:2008, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-11: Konstrukcje cięgnowe
- PN-EN 12385-2+A1:2008, Liny stalowe – Bezpieczeństwo, Część 2: Definicje, oznaczenie i klasyfikacja
- PN-EN 1993-1-4:2007, Projektowanie konstrukcji stalowych -Część 1- 4: Reguły ogólne -Reguły uzupełniające dla konstrukcji ze stali nierdzewnych
- PN-EN 10264:2012, Drut stalowy i wyroby z drutu – Drut stalowy na liny – Część 1: Wymagania ogólne
- 10264-4:2012, Drut stalowy i wyroby z drutu -Drut stalowy na liny -Część 4: Drut ze stali odpornej na korozję
- PN-EN 12385-4:2011, Zakończenia lin stalowych -Bezpieczeństwo – Część 4: Zalewanie metalem i żywicą
- PN-EN 12385-10+A1):2008, Liny stalowe -Bezpieczeństwo – Część 10: Liny jedno-zwite do ogólnych zastosowań w konstrukcjach technicznych
- PN-EN 13411-3:2007, Zakończenia lin stalowych – Bezpieczeństwo – Część 3: Tuleje i ich zaciskanie
- PN-EN 10138-3:2000, Prestressing steels – Part 3: Strand
- PN-EN 13411-4:2013, Zakończenia lin stalowych – Bezpieczeństwo – Część 4: Zalewanie metalem i żywicą
- PN-EN 13411-5:2009, Zakończenia lin stalowych – Bezpieczeństwo- Część 5: Zaciski linowe kabłąkowe
- Elamed, (2013), Przegląd zakotwień. Mosty, 02 [ http://mosty.elamed.pl/uploads/mos/articles/mosty_artykul_2013_02_38015.pdf ]
- PN-EN 1991-1-4:2008, Eurokod 1. Oddziaływania na konstrukcje, Część 1-4: Oddziaływania ogólne. Oddziaływania wiatru
- 1993-3-2+Ap1:2008, Eurokod 3-Projektowanie konstrukcji stalowych- Część 3-2: Wieże, maszty i kominy. Kominy
- PN-EN 1991-1-5:2005, Eurokod 1: Oddziaływania na konstrukcje, Część 1-5: Oddziaływania ogólne. Oddziaływania termiczne
- Galileusz, (1638). Dialogi o dwu najważniejszych układach świata: ptolemeuszowym i kopernikowym
- Petersen C., (2013), Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten, 4 Wydanie
- Pałkowski S., (2009), Konstrukcje stalowe: wybrane zagadnienia obliczania i projektowania, Wydawnictwo Naukowe PWN, Warszawa
- PN-EN 10028-2:2010, Wyroby płaskie ze stali na urządzenia ciśnieniowe – Część 2: Stale niestopowe i stopowe o określonych własnościach w podwyższonych temperaturach
- PN-EN 1993-1-9:2007, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-9: Zmęczenie
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 12385-1 +A1:2007, Liny stalowe – Bezpieczeństwo – Część 1: Wymagania ogólne
- Mehler Texnologies Sp. z o.o. (2015). Przewodnik techniczny po trwalej architekturze tekstylnej Mehler Texnologies, [ przewodnik-techniczny-po-trwalej-architekturze-tekstylnej-mehler-texnologies.pdf ]
- Technet GMBH (1989), Easy – Software fur die durchgangige Planung und Berech-nung Leichter Flachentragwerke, [http://technet-gmbh.de/index.php?id=63 ]
- Dlubal Software, (2019), RF-FORM-FINDING. Moduł dodatkowy dla RFEM Kształt membran i kabli, [ https://www.dlubal.com/pl/produkty/moduly-dodatkowe-dla-rfem-i-rstab/konstrukcje-membranowe/rf-cutting-pattern ]
- Sofistik, (2018), Sofistik. Imperfection Concept. Sofistik Tutorials 2018, Tutorilas for Stel Design. Imperfection Concept, [ /www.sofistik.de/documentation/2018/en/tutorials/steel-design/imperfection/imperfection.html ]
- Chodor L., (2016). Przekrycia hal i galerii. Materiały XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji, Tom I, ss. 25–202, [ https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf]
________________________________