Leszek Chodor, 3 listopada 2016
07-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 8 Czytelników
Podstawowymi elementami konstrukcji stalowych są belki i słupy. Belki są elementami zginanymi, a słupy ściskanymi Elementy te przed osiągnięciem pełnej nośności przekroju (plastycznej dla klasy 1-szej przekroju , lub 2-giej, sprężystej dla klasy 3-ciej lub pozakrytycznej dla klasy 4-tej) mogą utracić stateczność globalną elementu: słupy wybaczają się, a belki wichrzą i w związku z tym zasadniczo mają mniejszą nośność od przekroju pręta, z którego są wykonane. Pokazano, że siła krytyczna nie jest wartością własną pręta, ale zależy od sztywności całego systemu i od poziomu wytężenia pręta. Zaprezentowane zasady w istocie są już historyczne. Nie zaleca się ich stosowania w profesjonalnym projektowaniu, choć są przedstawiane z myślą o studentach Wydziału Architektury i także wstępnego kursu na Wydziale Budownictwa. Rozszerzenie tematu można znaleźć w artykule Współczynnik wyboczeniowy. Geneza i mit, w pracy [1] oraz podręczniku Imperfekcyjna metoda projektowania.
W niniejszym, artykule omówiono najprostszy przypadek pręta ściskanego osiowo siłą stała po jego długości zgodnie z historyczną metodą wyboczeniową. Taki przypadek w praktyce zdarza się incydentalnie. Rzeczywiste słupy są bowiem ściskane i zginane najczęściej dwukierunkowo z interakcją wyboczenia giętnego i zwichrzenia. Zagadnienia te w klasycznym, „studenckim” podejściu omówiono w artykule Słupy stalowe.
Wyboczenia pręta idealnego i rzeczywistego
Zadanie wyboczenia słupów ściskanych osiowo zostało rozwiązane już w XVIII w. przez Eulera (1707-1783) i znane jest pod nazwą teorii wyboczenia giętnego. Euler pokazał, że idealnie prosty i ściskany osiowo pręt sprężysty może mieć dwie postacie równowagi: pozostaje prostoliniowy w zakresie siły ściskającej $0<N\le N_{cr}$, a po pewnej krytycznej wartości $N_{cr}$ ulega nagłemu wygięciu (rys.1). Właśnie to zjawisko nazywa się wyboczeniem giętnym.
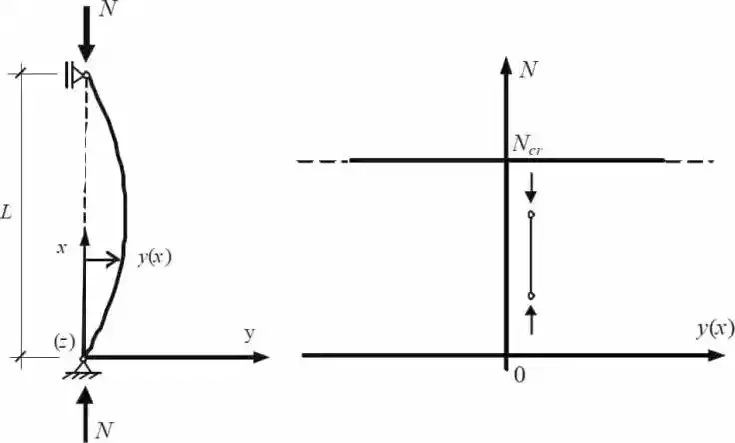
Rys.1. Wyboczenie słupa idealnego ((Simoes R. (2014). Eurocodes – Design of steel buildings with worked examples. Design of Members. ECCS))
Z elementarnego rozwiązania równania zginania i ściskania pręta idealnego (idealnie prostego i obciążonego idealnie osiowo, idealnie stałą siłą po długości), wynika że siła krytyczna $N_{cr}$ przy wyboczeniu w płaszczyźnie zawierającej oś $\bullet$, można zapisać formułą
$$\begin {equation} N_{cr \bullet}= \cfrac {\pi^2 \cdot EI_{\perp \bullet}}{L^2_{cr \bullet}}\label {1} \end {equation}$$
gdzie: E- moduł Younga materiału (dla stali E=210 GPa), $I_\bullet$- moment bezwładności przekroju pręta względem głównej, centralnej osi bezwładności przekroju $\bullet$, prostopadłej do płaszczyzny wyboczenia (np. przy wyboczeniu w płaszczyźnie $\bullet=y$, $I_{\perp \bullet}=I_z$.
$L_{cr}$ jest długością wyboczeniową pręta, zależną od długości teoretycznej $L$ oraz warunków podparcia. Zwykle zapisuje się
$$\begin {equation} L_{cr}=\mu \cdot L \label {2} \end {equation}$$
gdzie $\mu$ jest współczynnikiem długości wyboczeniowej. Można pokazać, że $\mu$ przyjmuje wartości z przedziału:
$$\begin {equation}\mu=0,5 \, do \, \infty \label {3} \end {equation}$$
gdzie $\mu=0,5$ odpowiada schematowi pręta utwierdzono-utwierdzonego ( o nieskończonych sztywnościach podpór w tym zamocowania), a $\mu= \infty$ odpowiada prętowi swobodnie zawieszonemu w przestrzeni (konstrukcja kinematycznie zmienna).
W tym miejscu najczęściej prezentuje się kilka podstawowych schematów statycznych prętów i podaje dla nich współczynniki długości wyboczeniowej. My NIE będziemy tego robić, albowiem NIE ma to większego znaczenia w analizach rzeczywistych konstrukcji, a może wprowadzić wiele zamieszania, na przykład przez przekonanie o tym, że maksymalna wartość współczynnika $\mu$ wynosi 2,0 (jak dla wspornika). Jest to oczywiście szkodliwa wiedza, bowiem współczynnik długości wyboczeniowej może być wielokrotnie większy od 2,0. Wprowadzenie do teorii współczynników długości wyboczeniowych dokonamy dopiero w rozdziale „Długosści wyboczeniowe_pretów_w_systemie”, w celu wykazania okoliczności jak w zdaniach poprzednich.
Następnie należy z całą mocą podkreślić, że rzeczywiste pręty ściskane (słupy) nie są idealne:
- oś pręta nie jest prosta ze względu na imperfekcje geometryczne osi pręta (wygięcia,
- słup nie jest pionowy, lecz ma imperfekcje przechyłowe,
- przekrój pręta nie jest stały pod długości, ze względu na imperfekcje charakterystyk przekroju,
- siła ściskająca nie jest idealnie stała po długości pręta, ale co gorsza ze względu na wstępne mimośrody przyłożenia do głowicy stupa -pręt w zasadzie od początku pracy jest obciążony dodatkowymi momentami zginającymi.
W związku z tymi niedoskonałościami wzór (1) również NIE ma większego znaczenia praktycznego. Jest bowiem słuszny wyłącznie dla pręta idealnego. Ma natomiast duże znaczenie poznawcze, w szczególności jako ważny przykład w teorii katastrof [2] oraz w opisie zjawiska wyboczenia i utraty stateczności w naukach podstawowych, (w tym przypadku matematyce, fizyce i mechanice).
Pręt rzeczywisty nie ulegnie wyboczeniu, bo od początku pracy jest zginany i ściskany, więc właściwa dla niego jest analiza drugiego rzędu, w której uwzględnia się wpływ przemieszczeń na siły przekrojowe.
W przypadku obciążenia pręta jednoczesnym zginaniem i ściskaniem stosowany przez inżynierów wzór wytrzymałościowy na naprężenia normalne zwykle zapisuje się w postaci:
$$\begin {equation}\sigma=\sigma_M+\sigma_N=\cfrac{M}{I} \cdot z +\cfrac{N}{\chi \cdot A} \le f_y \label {4} \end {equation}$$
lub w przestrzeni sił przekrojowych w postaci:
$$\begin {equation} \cfrac{M}{M_R} +\cfrac{N}{\chi \cdot N_R} \le 1 \label {5} \end {equation}$$
gdzie: $(M,N)$ – moment zginający i siła osiowa w przekroju krytycznym pręta, $M_R=W f_y$, $N_R=A f_y$, $I$- moment bezwładności pręta, $z$- odległość punktu przekroju od osi obojętnej, $A$- pole przekroju pręta, $W$- wskaźnik wytrzymałości przekroju, $f_y$ – granica plastyczności oraz $\chi$ współczynnik wyboczeniowy,
NIE ma to przekonywującego uzasadnienia teoretycznego, a wynika z przybliżonej teorii Ayrton- Perry . Z wielu argumentów podnoszonych w krytyce takiego podejścia wymienimy tylko dwie:
1) sumowanie naprężeń od zginania $\sigma_M$ z naprężeniami od ściskania $\sigma_N$ jest nieprawidłowe z powodu nieobowiązywania zasady superpozycji w obszarach nieliniowych, bliskich stanom granicznym,
2) wyznaczanie współczynnika wyboczenia w złożonym stanie naprężenia jest nieprawidłowe, bo pręt zginany nie może ulec wyboczeniu,
Tym niemniej w praktyce inżynierowie chętnie stosowali i niestety nadal chętnie stosują, aproksymację ($\ref{4}$) lub ($\ref{5}$) ze względu na: a) trudności obliczeniowe w erze przedinformatyzacyjnej, oraz b) wystarczające dla praktyki przybliżenia uzyskiwane z tych wzorów.
Wymiarowanie pręta ściskanego według Eurokodu 3
Podstawy normowe
Formułę (\ref{5}) w prostym przypadku obciążenia, ściskania pręta, można zapisać w przestrzeni sił przekrojowych w sposób [3],(6.46):
$$\begin {equation} \cfrac{N_{Ed}} {N_{b,Rd}}\le 1\label {6} \end {equation}$$
gdzie: $N_{Ed}$ – obliczeniowa siła ściskająca, $N_{b,Rd}$- nośność na wyboczenie elementu ściskanego
Nośność na wyboczenie elementu ściskanego należy obliczać z zależności [3],(6.46):
$$\begin {equation} N_{b,Rd} \le \cfrac{\chi A_k f_y}{\gamma_{M1}} \label {7} \end {equation}$$
gdzie: $A_k$ pole przekroju pręta zależne od klasy przekroju: $A_k =A$ dla 1,2 i 3 klasy oraz $A_k = A_{eff}$ dla klasy 4-tej. Współczynnik materiałowy dla elementu przy sprawdzaniu warunków stateczności $\gamma_{M1}=1,1$.
Współczynnik wyboczeniowy $\chi$ zależy od smukłości względnej pręta
$$\begin {equation} \overline \lambda =\sqrt{\cfrac{A_k \cdot f_y}{N_{cr}}} \label {8} \end {equation}$$
i jest wyznaczany z formuły [3], (6.49):
$$ \begin {equation} \phi=0,5\left [ 1+\alpha \cdot (\overline \lambda-0,2)+\overline \lambda^2\right] \label {9} \end {equation}$$
W przypadku elementów o smukłości $\overline \lambda <0,2$ warunek stateczności elementu sprowadza się do sprawdzenia nośności przekroju.
Parametr klasy imperfekcji $\alpha$ przyjmuje się w zależności od klasy imperfekcji ( rodzaju krzywej wyboczeniowej), przypisanej do kształtu przekroju, na podstawie tab.1 i tab.2
Tab.1. Parametry imperfekcji $\alpha$ krzywych wyboczeniowych
[3], tab. 6.1
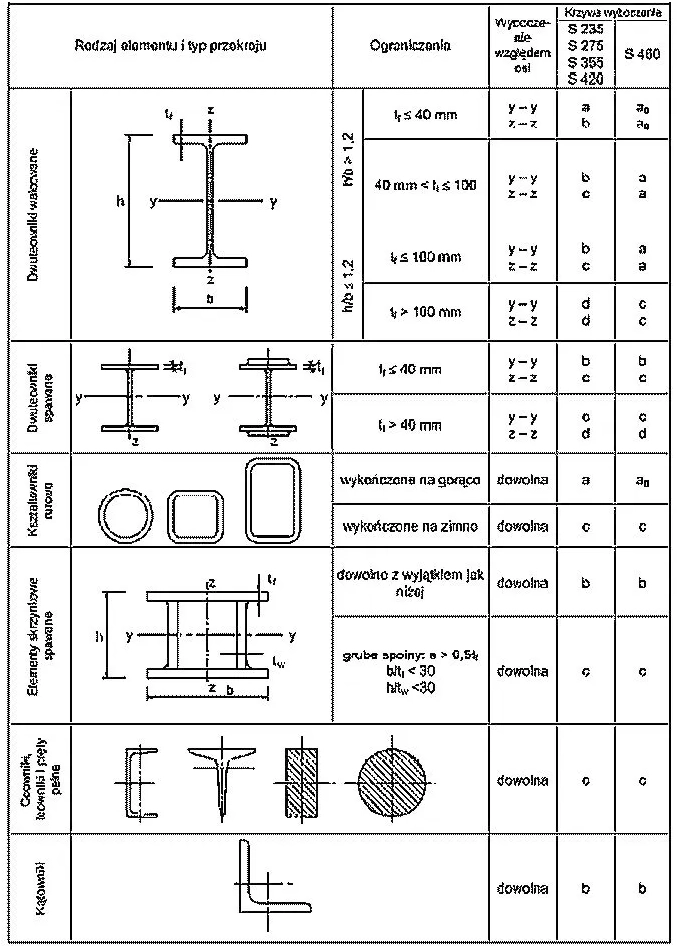
Tab.2. Przyporządkowanie krzywych wyboczenia do rodzaju przekroju stalowego
[3], tab. 6.2.
Wykres zależności współczynnika wyboczenia ($\ref{9}$) od smukłości względnej ($\ref{8}$) uzyskany z powyższych formuł zobrazowano na rys.2.
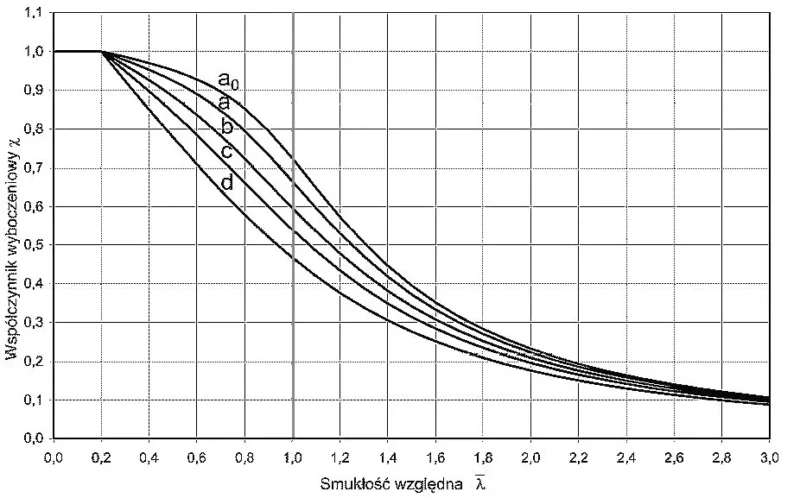
Rys.2. Krzywe wyboczenia stalowych prętów [3], rys. 6.1.
Po podstawieniu eulerowskiej siły krytycznej ($\ref{2}$) w zapisie $N_{cr}=\cfrac{ \pi^2 \cdot EI}{L_{cr}^2}$ do (\ref{8}) otrzymamy wyrażenie na smukłość względną w postaci [3],(6.50) – (6.51):
$$\begin {equation} \overline \lambda = \sqrt{\cfrac{A_k \cdot f_y }{N_{cr}}} = \cfrac{L_{cr}}{i} \cdot \cfrac{1}{\lambda_1} = \cfrac{\lambda}{\lambda_1} \label {10} \end {equation}$$
gdzie:
smukłość elementu $ \lambda=\cfrac{L_{cr}}{i}$
promień bezwładności przekroju $i= \sqrt{ \cfrac{I}{A_k}}$,
smukłość porównawcza $\lambda_1= \pi \cdot \sqrt{ E / f_y }=93,9 \cdot \varepsilon$.
współczynnik gatunku stali $\varepsilon=\sqrt{235/f_y)}$, ($f_y$ w [MPa]).
Współczynnik $\varepsilon $ dla poszczególnych stali wynosi: S235 – 1,00 ; S275 – 0,924; S355 – 0,814.
Formuły (\ref{8}) i (\ref{10}) są tożsame, to znaczy wyznaczenie $N_{cr}$ ze wzoru Eulera i podstawienie do (\ref{8}) nie może dać innego rezultatu od wartości, uzyskanej bezpośrednio z (\ref{10}). W celu uzyskania lepszego wyniku należy wyznaczyć siłę krytyczną pręta w inny sposób niż z wzoru Eulera – polecane są współczesne programy obliczeniowe, np. LTBeam lub Consteel.
Wyznaczanie siły krytycznej ze wzoru Eulera jest obarczone dużą niepewnością, wynikającą z tego, że zależy od poprawnego przyjęcia długości wyboczeniowej $L_{cr}$, a to w praktycznych przypadkach rzeczywistych konstrukcji nie jest zadaniem banalnym. Większość ram stalowych jest przesuwna, a więzy są odkształcalne (nie są w pełni przegubowe, czy też sztywne). W takiej sytuacji szacowanie długości wyboczeniowych na podstawie prostych schematów statycznych znanych z mechaniki, prowadzi do bardzo istotnych błędów. Błąd ten wzmacnia się przy wyznaczaniu współczynnika wyboczenia, który jest silnie nieliniową funkcją długości wyboczeniowej.
Dlatego należy sformułować wniosek:
Wyznaczanie współczynnika wyboczenia z formuły ($\ref{10}$) NIE ma większego znaczenia praktycznego w analizach rzeczywistych konstrukcji. Smukłość słupa osiowo ściskanego wyznaczamy bezpośrednio z formuły (\ref{8}), a siłę krytyczną $N_{cr}$ należy przyjąć z rozwiązania pomocniczego zadania mechaniki – problemu wyboczenia z wykorzystaniem numerycznych procedur MES dla całego systemu konstrukcyjnego, do którego przynależy słup.
Elementy ściskane i zginane
Elementy ściskane i zginane są najczęściej spotykanymi elementami stalowymi. W zasadzie (p. pkt.1) wszystkie rzeczywiste elementy ściskane są jednocześnie zginane. Poniżej zamieszczono krótkie wprowadzenie do zagadnienia. Rozwinięcie zagadnienia zawiera artykuł Stalowe słupy hal, w którym zdefiniowano element belka-słup.
Zgodnie z [3], wzór (6.61)-(6.62) warunki nośności elementów zginanych i ściskanych są następujące:
$$\begin{equation} \cfrac{N_{Ed}}{\chi_y \cdot N_{Rd}}+ \cfrac{ k_{yy} M_{y,Ed}}{\chi_{LT} \cdot M_{y, Rd}} + \cfrac{ k_{yz} M_{z,Ed}}{ M_{z,Rd}} + \cfrac{B}{B_{Rd}} \le 1 \\
\cfrac{N_{Ed}}{\chi_z \cdot N_{Rd}}+ \cfrac{ k_{zy} M_{y,Ed}}{\chi_{LT} \cdot M_{y,Rd}} + \cfrac{ k_{zz} M_{z,Ed}}{ M_{z,Rd}} + \cfrac{B}{B_{Rd}} \le 1 \label {11} \end{equation}$$
gdzie:
$N_{Ed}$, $M_{y,Ed}$, $M_{z,Ed}$- obliczeniowa siła osiowa, maksymalny na belce moment zginający względem osi y oraz maksymalny moment zginający względem osi z,
$\Delta M_{y,Ed}$ i $\Delta M_{z,Ed}$ – ewentualne dodatkowe momenty, spowodowane przesunięciem środka ciężkości przekroju klasy 4 na skutek zredukowania jego przekroju do przekroju efektywnego wg tab 3.
$N_{Rd}$, $M_{y,Rd}$, $M_{z,Rd}$, $B_{Rd}$ – obliczeniowe nośności mierzone: siłą osiową, momentem zginającym względem osi y i względem osi z oraz bimomentem,
Nośności obliczeniowe $F_{Rd}$, to nośności charakterystyczne przeskalowane materiałowym współczynnikiem bezpieczeństwa $\gamma_{M1}$ : $F_{Rd}=\cfrac{F_{Rk}}{\gamma_{M1}}$
$\chi_y$ , $\chi_z$ −współczynniki wyboczenia giętnego względem stosownych osi,
$\chi_{LT}$ – współczynnik zwichrzenia,
kyy, kyz, kzy, kzz– współczynniki interakcji, które można obliczać każdą naukowo i technicznie uzasadnioną metodą (wybór w zasadzie zależy od inżyniera -projektanta) W normie [3], (6.61)-(6.62)}”] podano przykładowo dwie metody: metoda 1 (załącznik A) i metoda 2 (Załącznik B).
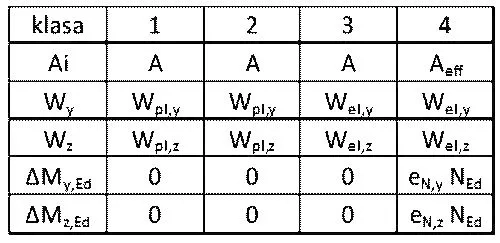
Tab.3. Definicje charakterystyk geometrycznych prętów z przekrojami różnych klas [3], tab 6.7
Długości wyboczeniowe prętów w systemie
Geometryczna interpretacja długości wyboczeniowej
Na rys. 3 zestawiono klasyczne, standardowe przypadki I do VI prętów i stosowne współczynniki długości wyboczeniowych $\mu$ do formuły ($\ref{2}$).
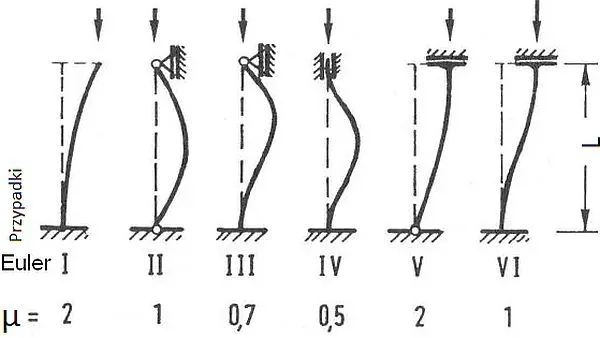
Rys.3. Teoretyczne współczynniki długości wyboczeniowej dla podstawowych przypadków Eulera [4]
Standardowe przypadki Eulera w praktyce nie wystąpią , przede wszystkim dlatego, że sztywności węzłów nie są idealne. Konsekwencje pokażemy w kolejnych punktach.
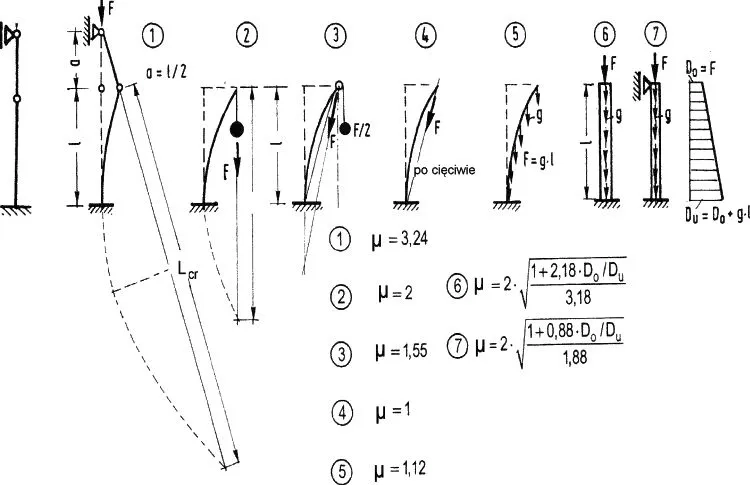
Rys.4 Teoretyczne współczynniki długości wyboczeniowej dla przypadków złożonych i sens geometryczny [4]
W bardziej złożonych przypadkach użyteczna jest interpretacja geometryczna długości wyboczeniowej. Na tej podstawie można skutecznie określić długość wyboczeniową w złożonym przypadku pręta. Oceny dokonujemy po oszacowaniu osi wygiętego pręta jako długość cięciwy prostopadłej do łuku odkształconej osi. Wynikające z takiego podejścia współczynniki długości wyboczeniowej – na rys. 4 oszacowano dla 7-miu szczególnych przypadków.
Długość wyboczeniowa zależy od sztywności całej konstrukcji
Rozpatrzmy przykład prostej ramy, złożonej ze słupa i rygla w sposób pokazany na rys.5.
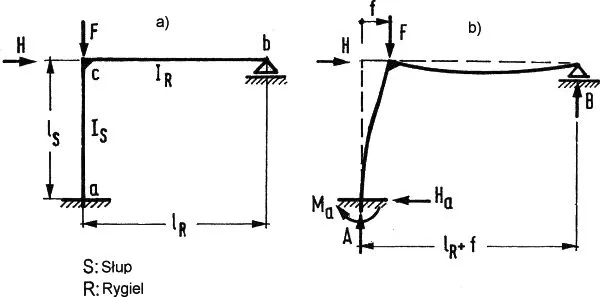
Rys. 5 Przykład ramy do wyznaczenia długości wyboczeniowej słupa: a) przed odkształceniem, b) po obciążeniu, [4], rys.20
W pracy Peterse (2013) [4] pokazano ścisłe rozwiązanie problemu wg teorii II rzędu, które dla $H=0$ (dla zagadnienia wyboczenia) zależne od parametru
$$\begin{equation} \kappa=\cfrac{EI_S}{EI_R}\cdot\frac{l_R}{l_S} \label {12} \end{equation}$$
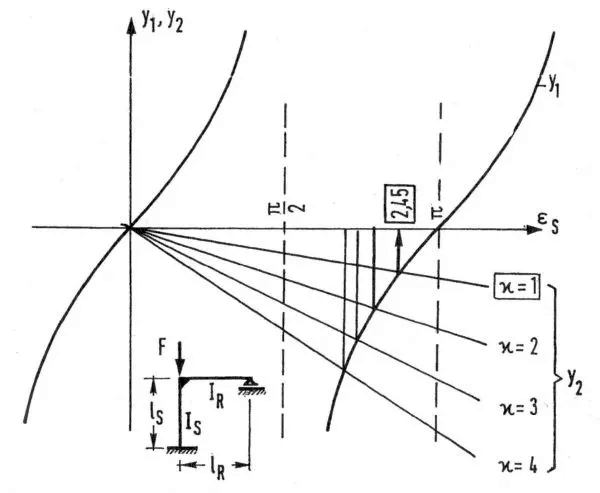
Rozwiązanie graficzne, pokazane na rys. 6 przedstawia zmienną $y_1=tan (\varepsilon_S)$ w funkcji parametru $\kappa$ (11).
Wartość rzędnej $\varepsilon_S =l_S \sqrt {\frac{A}{EI_S}}$ (A jest reakcją 2-rzędu stopy słupa). Dla $\kappa=1$ – z rys.6 odczytujemy rozwiązanie zagadnienia poprzez rzutowanie punktu przecięcia $y_1$ z $\kappa$. Dla $\kappa=1$ otrzymamy $\varepsilon_S=2,45$.
Z porównania $\cfrac{\pi^2 EI_S}{(\mu\cdot l_S)^2}=2,45^2 \cdot \cfrac{EI_S}{l_S^2}$ uzyskujemy $ \mu = 1,28$.
Pokazaliśmy, że w przypadku słupa idealnie utwierdzonego w podłożu i w głowicy współczynnik długości wyboczeniowej jest znacznie większy od 0,5 lub 1 i dla identycznych belkowych sztywności rygla i słupa może wynosić 1,28 .
Rozważania dla innych przypadków było przedmiotem wielu prac. W kolejnym punkcie podamy praktycznie użyteczne aproksymacje długości wyboczeniowych słupów ram w układach wielokondygnacyjnych.
Nomogramy do wyznaczania długości wyboczeniowych wg PN-90/B-03200
W „starej” polskiej normie „Konstrukcje stalowe – Obliczenia statyczne i projektowanie” [5], Z1-3 zamieszczono użyteczne nomogramy do wyznaczania długości wyboczeniowych prętów.
Na rys. 7 pokazano nomogram do wyznaczania długości wyboczeniowych słupów układów przesuwnych (ang unbraced).
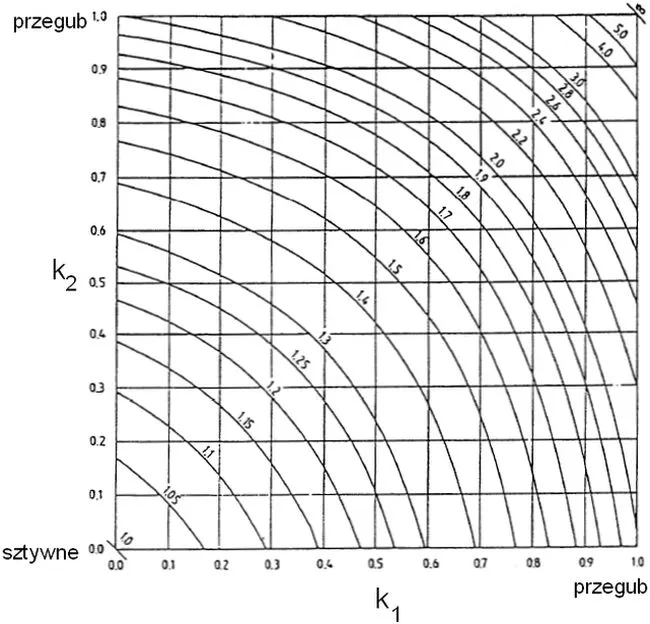
Rys 7 Nomogram współczynnika wyboczenia dla układów przesuwnych [zmodyfikowane [5], Z1-3
Osie współrzędnych nomogramu są podatnościami węzłów dolnego $k_1$ i górnego $k_2$ słupa ( w przypadku belek-słupów będzie to odpowiednio koniec lewy i prawy).
W praktyce rzadziej stosuje się układy o węzłach nieprzesuwnych dla których nomogram jest istotnie inny, jak pokazano na rys. 8.
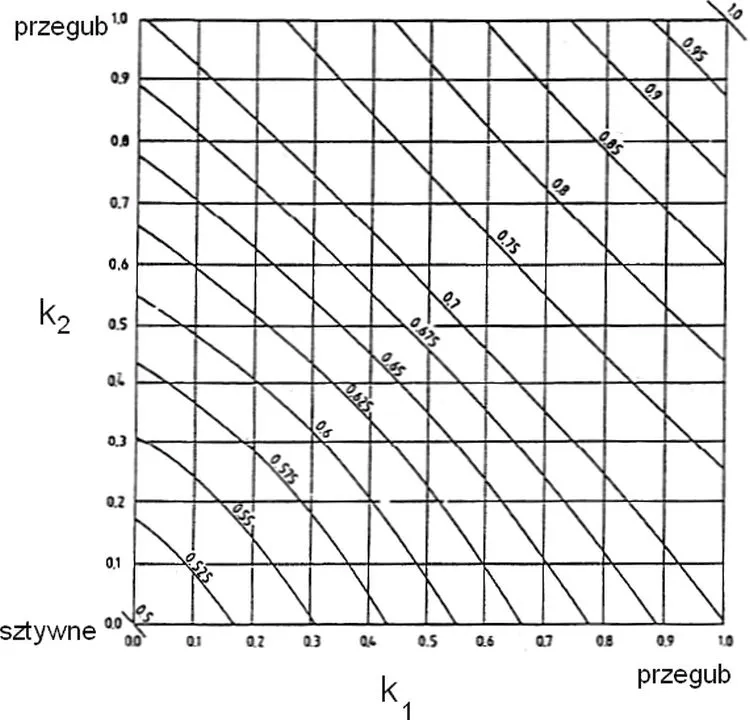
Rys 8 Nomogram współczynnika wyboczenia dla układów nieprzesuwnych [zmodyfikowane [5] ,Z1-3
Stopień podatności węzłów wyznacza się z zależności:
$$\begin{equation} k_i= \cfrac{\overline K_S}{\overline K_S+\overline K_R} \, \ge 0,3 \label {13} \end{equation}$$
w której:
$\overline K_S=\cfrac{I_S}{l_S}$ – względna sztywność słupa (w stosunku do modułu Younga E)
$\overline K_R=\sum \limits_{(i)} \left( \eta \cfrac {I_R}{l_R}\right)$ – względna sztywność rygli,
przy czym:
$ \sum \limits_{(i)}$ – sumowanie obejmuje elementy (bez słupa) leżące w płaszczyźnie wyboczenia i sztywno połączone ze słupem w rozpatrywanym węźle (i=1, 2),
$\eta$ – współczynnik uwzględniający warunki podparcia na drugim końcu belki-rygla. W przypadku układu o węzłach przesuwnych (w nawiasie nieprzesuwnych):
$\eta=1,5 (0,5)$ przy podparciu przegubowym,
$\eta=2,0 (1,0)$ przy sztywnym utwierdzeniu:
Dla stopy sztywnej (przenoszącej ściskanie ze zginaniem) można przyjmować $ K_F = K_S $, a w pozostałych przypadkach $ \overline K_F = 0,1 \cdot \overline K_S $. W formule ($\ref{13}$) dla węzła podporowego $\overline K_F$ traktuje się jako $ \overline K_R$ .
Długości wyboczeniowe słupów ram portalowych
W pracy [4]) przeanalizowano ramy jednokondygnacyjne o kształcie pokazanym na rys.9, przy czym słup może być przegubowo oparty na fundamencie lub w nim zamocowany.
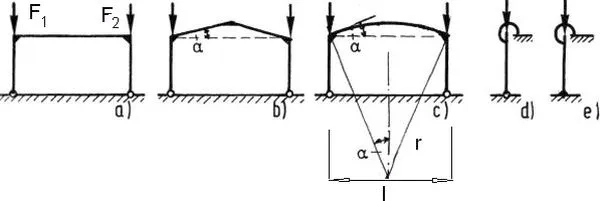
Rys.9 Ramy portalowe: a) o poziomym rygle, b) pochyły , c) łukowy, d) stopa przegubowa, e) stopa zamocowana
Stopa przegubowa realizuje się w sposób pokazany na rys. 10a, a utwierdzenie 10 b),c).
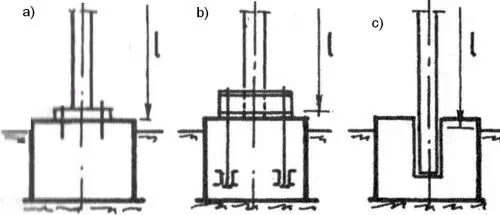
Rys.10. Stopa słupa stalowego: a) przegubowa, b,c)- utwierdzona [4],rys. 115
W przypadku równych sił w slupach ramy portalowej współczynniki długości wyboczeniowej słupów można dobierać z nomogramów pokazanych na rys. 11
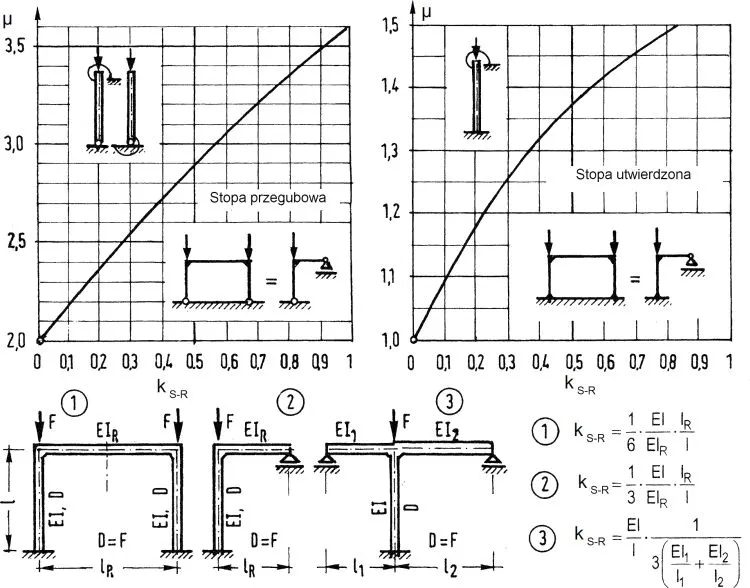
Rys. 11. Współczynniki długości wyboczeniowych słupów ram portalowych $\mu$ w funkcji współczynnika stosunku sztywności $k_{S-R}$
Współczynnik stosunku sztywności słupa i rygla $k_{S-R}$ należy przyjmować z zależności zestawionych na rys. 11. Podstawową wartość opisuje formuła:
$$\begin{equation} k_{S-R}=\frac{EI_S/l_S}{K_R} \label {18} \end{equation}$$
gdzie sztywność rygla wynosi:
dla rygla prostego (rys. 11a) $K_R=\frac{6EI_R}{l_R}$,
dla rygla pochyłego (rys. 11b) $K_R=\frac{6EI_R}{l_R}\cdot cos\alpha$,
dla rygla łukowego (rys. 11c) $K_R=\frac{6EI_R}{l_R}\cdot\frac{1}{2\left( \cfrac{r}{l \cdot sin\alpha \cdot cos\alpha – \alpha}\right)}$.
W przypadku różnych sił działających w słupach należy wyznaczyć spodziewany stosunek
$$\begin{equation} m=\cfrac{ min F}{max F}=\cfrac{F_1}{F_2} \label {19} \end{equation}$$
a następnie współczynniki korekcyjne dla słupa 1 i 2:
$$\begin{equation} \alpha_1 \sqrt{0,5(1+m)} \le 1,0$, $\alpha_2=\alpha_1 \cdot \sqrt{m} \label {20} \end{equation}$$
Ostatecznie współczynnik długości wyboczeniowej dla słupa 1 wynosi:
$$\begin{equation} \mu_1=\mu \cdot \alpha_1 \label {21} \end{equation}$$
Długości wyboczeniowe zależą od obciążenia (stopnia wytężenia) pręta
W wielu pracach pokazano, że sztywność wyodrębnionego z systemu pręta ściskanego (lub rozciąganego) zależy od wielkości obciążenia. Na rys.11 pokazano zależność sztywności pręta (ściskanego lub rozciąganego) z głowicą przesuną o $\Delta$ od stopnia obciążenia. Przy braku obciążenia sztywność jest zerowa, dla $N=N_{cr,L}$, czyli przy obciążeniu silą ściskającą Eulera odpowiadającą $\mu=1$ sztywność jest nieskończenie duża, co wynika z formuł ścisłych, ale też formuły aproksymacyjnej (zmieniono oryginalne oznaczenie sztywności $\alpha$ na $K$):
$$\begin{equation} K=-\cfrac{2EI}{L} \cfrac{(\pi^2/4)(N/N_{cr})}{1- N/N_{cr}} \label {14} \end{equation}$$
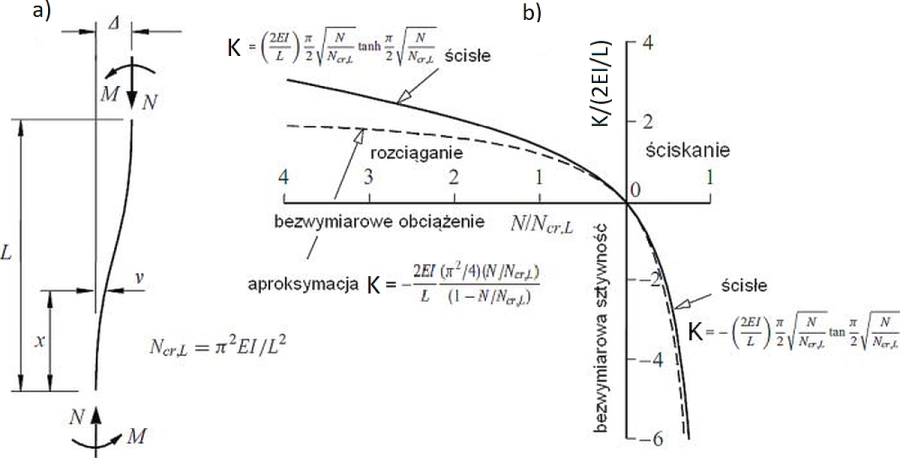
Rys.12 Sztywność pręta przesuwnego w funkcji obciążenia: a) schemat pręta z głowica przesuwną o $\Delta$, b) wykres sztywności $K$ : formuły ścisłe i aproksymacja [6], rys.3.18
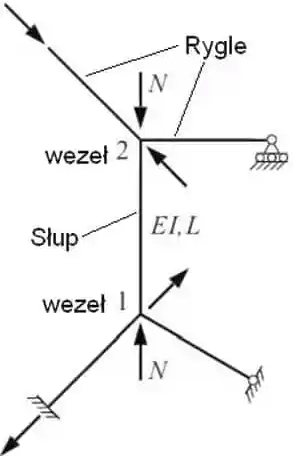
Rys.12 Słup w systemie prętów [6] rys. 3.17
Przykład 1 [ nośność słupa – klasyczna metoda normowa]
Przykład numeryczny za pracą Simones (2014) [7]
Sprawdzić wytrzymałość słupa wykonanego z kształtownika HEB340- S355 ściskanego osiowo w układzie konstrukcyjnym pokazanym na rys. 13.
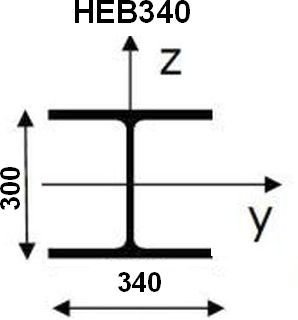 Charakterystyki geometryczne HEB340: h=300 mm, b=340 mm, tw=12 mm, tf=21,5 mm, A=170,9 cm2, iy=14,65 cm, iz=7,53 cm.
Charakterystyki geometryczne HEB340: h=300 mm, b=340 mm, tw=12 mm, tf=21,5 mm, A=170,9 cm2, iy=14,65 cm, iz=7,53 cm.
Parametry stali S355: fy = 355 MPa, $\varepsilon=\sqrt{235/355}=0,814$
Z rozwiązania układu konstrukcyjnego i po wyliczeniu kombinacji uzyskano obliczeniową siłę ściskającą słup
$N_{Ed}=3326,0 \, kN$.
Zarówno w głowicy jak i w stopie skonstruowano przestrzenne przeguby.
Taki słup jest wyjątkowym przypadkiem i jest nazywany wahaczem.
Długości wyboczeniowe w obu płaszczyznach są takie same i są równe długości teoretycznej $L_{cr, y} =L_{cr, z}=L$
Odległość między przegubami jest wysokością kondygnacji budynku i wynosi 4335 mm. Długość wyboczeniowa jest taka sama w obu płaszczyznach: w płaszczyźnie ramy (x-y) – wyboczenie wokół osi z i z płaszczyzny ramy (x-z) – wyboczenie wokół osi y: $L{cr,z}=L{cr,y}=435 cm$.
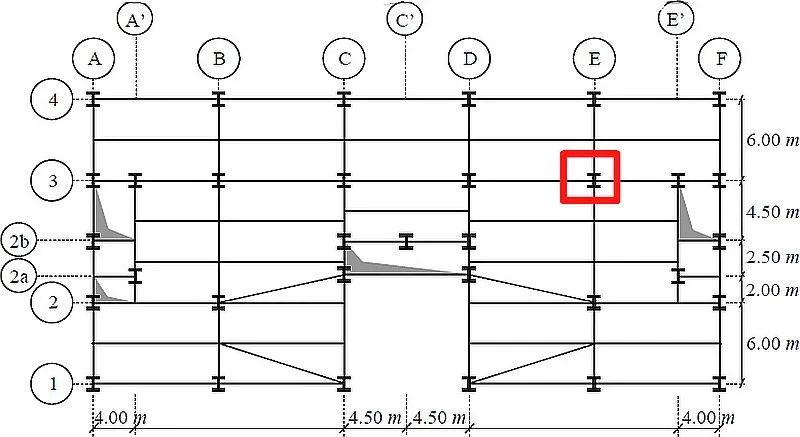
Rys.13. Plan główny konstrukcji z oznaczonym słupem do przykładu [7]
Klasa przekroju
W przykładzie artykułu klasa przekroju, pokazano, że środnik, pas i cały przekrój HEB340-S355, jest klasy 1 .
Sprawdzenie nośności przekroju
$N_{Ed}=3326,0 \ kN \le N_{Rd}= \cfrac {A f_y}{\gamma_{M0}}=\cfrac {170,9 \cdot 10^{-4}\cdot 355 \cdot 10^{3}}{1,0}=6067,0 \ kN $
Współczynnik wyboczeniowy [analitycznie]
$\lambda_1=93,9 \cdot 0,814=76,41$,
Ponieważ $h/b=340/300=1,13 \le 1,2$ oraz $t_f=21,5 < 100 \,mm \to$ (tab.2),
to mamy krzywe wyboczeniowe:
przy wyboczeniu wokół osi (y) – „b” ($\alpha=0,34 $),
przy wyboczeniu wokół osi (z) – „c” ($\alpha=0,49 $).
Wyboczenie z płaszczyzny (wokół osi y)
$\lambda_y=\cfrac{433,5}{14,65}=29,59$, $\overline \lambda_y=\cfrac{29,7}{76,41}=0,39$,
$\phi_y=0,5+[1+0,34\times(0,39-0,2)+0,39^2)]=0,61 $
$\chi_y= \cfrac {1} {0,61+ \sqrt {0,61^2-0,39^2}}=0,93 $
Wyboczenie w płaszczyźnie (wokół osi z)
$\lambda_z=\cfrac{433,5}{7,53}=57,57$, $\overline \lambda_z=\cfrac{57,57}{76,41}=0,75$
„c” $\to \alpha=049 $,
$\phi_z=0,5+[1+0,49\times(0,75-0,2)+0,75^2)]=0,92 $
$\chi_z= \cfrac {1} {0,92+ \sqrt {0,92^2-0,75^2}}=0,69 $
$\chi= \min \{ 0,93 ; 0,69 \}= 0,69$.
Współczynniki wyboczeniowy [z wykresu]
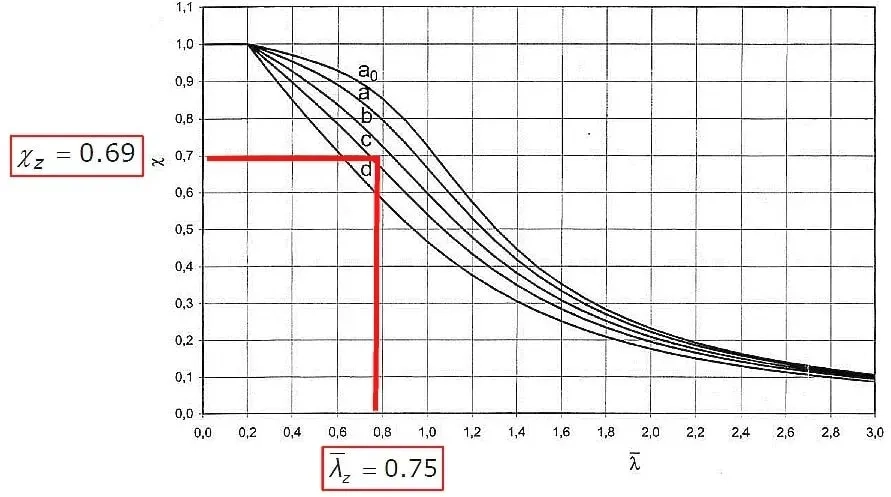
Rys.16 Wyznaczenie współczynnika wyboczenia z wykresu [7]
Sprawdzenie nośności elementu
$3326,0 \ kN \le \cfrac {0,69 \cdot 170,9 \cdot 10^{-4}\cdot 355 \cdot 10^{3}}{1,1}= 3805,64 \ kN $
Przykład 2 [Długość wyboczeniowa słupa dla różnych poziomów obciążenia]
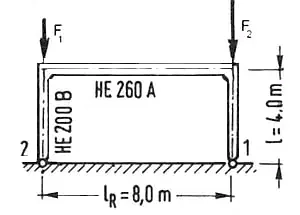
Wyznaczyć długość wyboczeniową słupa ramy pokazanej na rys. 17 dla danych:
Rygiel HEA 260 ($I_R=10455 cm^4 $),
Słupy HEB200 ($I_S=5696 cm^4$),
Stosunek obciążenia .$m=\cfrac {F_1}{F_2}= 0,75$.
Długość wyboczeniowa z nomogramu PN/B
Rama jest układem o węzłach przesuwnych w płaszczyźnie. Wnormie [5] nie uwzględnia się poziomu obciążenia , ani różnicy obciążeń słupów.
Sztywność rygla $\overline K_R= \cfrac{10445}{800}=13,06 cm^3$
Sztywność słupa $\overline K_S= \cfrac{5696}{400}= 14,2 cm^3$
Sztywność zamocowania $\overline K_F= 0,1 \cdot 14,2=1,4 cm^3$ (stopa jest przegubowa)
Współczynnik podatności węzła dolnego $k_1= \cfrac{14,2}{14,2+1,4}=0,91$
Współczynnik podatności węzła górnego $k_2=\cfrac{14,2}{14,2+13,06}= 0,52$.
Z nomogramu rys. 9 po interpolacji liniowej odczytujemy $\mu=0,78$
Długość wyboczeniowa słupa $L_{cr}=0,78 \cdot 400=312 cm$.
Długość wyboczeniowa z nomogramu Petersena
rys 14 [4]
Dla współczynnik stosunku sztywności słupów i rygla wynosi $k_{S-R}=\cfrac{1}{6}\cfrac{EI_S}{EI_R} \cfrac{l_R}{l_S}=\cfrac{1\cdot5696\cdot8,0}{6\cdot 10455\cdot 4,0}=0,182$,
z nomogramu rys. 14 dla ramy ze stopami przegubowymi i równych sił w słupach $\to \mu=2,34$.
Ponieważ siły w słupach różnią się ($m=\cfrac{F_1}{F_2}=0,75$), więc współczynnik korekcyjny wynosi $\alpha_m=\sqrt{0,5(1+0,75)}=0,935$.
Ostatecznie:
Współczynnik długości wyboczeniowej słupa 1: $\mu_1=0,935 \cdot 2,234=2,20$,
Współczynnik długości wyboczeniowej słupa 2 $ \mu_2=\cfrac{2,20}{\sqrt{0,75}}=1,91$
długość wyboczeniowa słupa 1: $L_{cr,1}=2,20\cdot 400=880 cm$,
długość wyboczenia słupa 2: $L_{cr ,2}=1,91 \cdot 400= 762 cm$
Pokazano , że długości wyboczeniowe słupów o takiej samej geometrii i warunkach podparcia różnią się o kilkanaście procent, a wyznaczone na podstawie różnych nomogramów nawet o ponad 100%.
Literatura
- Chodor, L. (2016). Przekrycia hal i galerii. In XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji: Vol. I (pp. 25–202). https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf
- Thom, R., Giorello, G., Morini, S., & Duda, R. (1991). Parabole i katastrofy: rozmowy o matematyce, nauce i filozofii z Giulio Giorello i Simoną Morinii, Państwowy Instytut Wydawniczy
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Petersen C. (2013). Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
- PN-90/B-03200, Konstrukcje stalowe – Obliczenia statyczne i projektowanie
- Trahair N. S., Bradford M. A. (2008), The Behaviour and Design of Steel Structures to EC3 (4th ed.), [ http://library.magistersipil.janabadra.ac.id/wp-content/uploads/2015/05/The-Behaviour-And-Design-Of-Steel-Structures-To-EC3-4th-EDITION.pdf ]
- Simoes R. (2014). Eurocodes – Design of steel buildings with worked examples. Design of Members. ECCS
________________________________