Ściany (tarcze) żelbetowe są elementami budynków ścianowo -płytowych, ale także ścian oporowych i innych konstrukcji inżynierskich. Ściany i tarcze są elementem przeważająco ściskanym i ścinanym.
Ściany mogą być zbrojone nośnie, gdy stopień zbrojenia $A_s \ge A_{s, min}$ lub „słabo zbrojone” (betonowe). W zależności od tego stosowane są różne sposoby analizy: dla ścian nośnych klasyczne metody konstrukcji żelbetowych (słupy, tarcze), a dla kruchych ścian betonowych należy stosować metody liniowej teorii sprężystości lub mechaniki kruchego pękania.
W niniejszym artykule nie rozróżniamy ścian od tarcz żelbetowych, bowiem w istocie są to takie same elementy konstrukcyjne.
Konstrukcja ścian i tarcz
Uwagi ogólne
Tarcze są często nazywane ścianami-belkami, ponieważ często zawierają otwory, które pracują na zginanie jak belki.
Współcześnie rozróżnienie ścian i tarcz straciło na znaczeniu, ponieważ oba elementy są analizowane w programach komputerowych jako cienkie powłoki obciążone w swojej płaszczyźnie (np. program ABC Tracza). Możliwe jest także analizowanie powłok obciążonych w płaszczyźnie i poprzecznie do niej (np. od parcia wiatru), co jest połączeniem tarczy i płyty.
Na znaczeniu straciły również zalecenia dotyczące smukłości ścian oraz utraty stateczności ściskanej strefy tarczy, ponieważ standardowo już analizy są już prowadzone metodami drugiego rzędu z obciążeniem imperfekcjami (np. program Consteel) .
Wymagania konstrukcyjne
Minimalne grubości ścian i tarcz
Minimalne grubości ścian i tarcz $t$ wynikają z warunków technologicznych, a mianowicie zachowania odpowiedniego otulenia oraz minimalnych odległości zbrojenia, umożliwiających prawidłowe zagęszczenie betonu. Z tych warunków grubość $t$ nośnych ścian żelbetowych zwykle nie powinna być mniejsza od 150 mm, a tarcz od 140 mm.
W przypadku wysokich ścian ogranicza się też jej smukłość:
$$\begin{equation} \lambda= \cfrac{l_{ef}}{t} \le 25 \label{lam} \end{equation}$$
Dla ścian budynków o wysokości ok 3500 mm mamy stąd $t \ge 3500/25=140 \, mm$
Długość efektywna zależy od warunków podparcia ściany:
$ l_{ef}= \beta l_0 $, gdzie:
l_0 – jest wysokością ściany w osiach podpór (w świetle + grubość stropu)
$\beta$ współczynnik zależny od warunków podparcia: $\beta=1$ dla ściany przegubowo-przegubowej, $\beta=2$ dla wspornika, $\beta=0,8$ dla ścian sprężyście utwierdzonych w stropach.
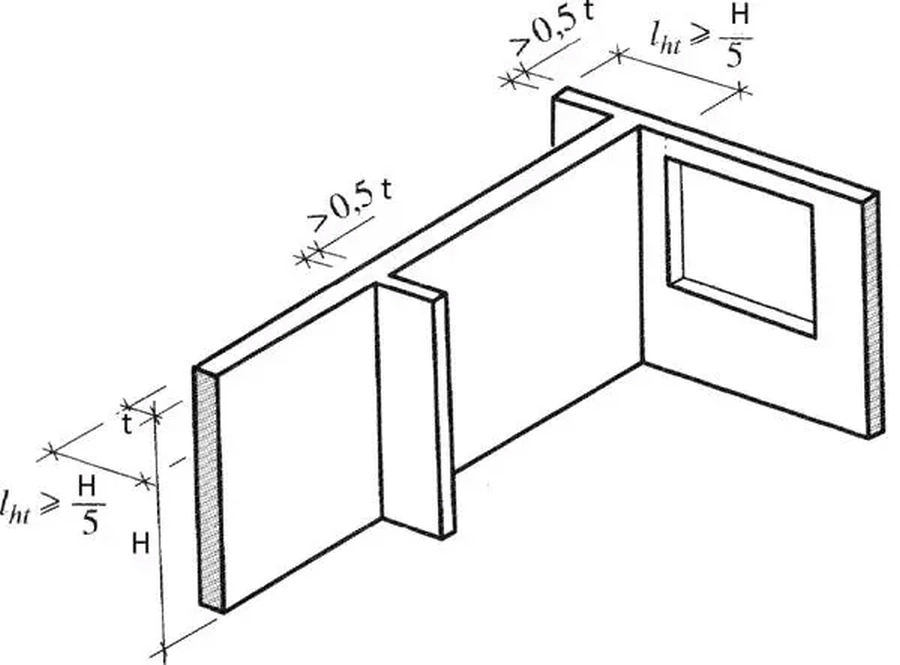
Istotne jest także podparcie ściany w pionie przez ściany usztywniające, co ogólnie prowadzi do zmniejszenia współczynników długości efektywnej $\beta$. Ścianę można uznać za usztywniającą , jeśli spełnia warunki z rys.1.
Rys.1. Warunki dla ściany usztywniającej
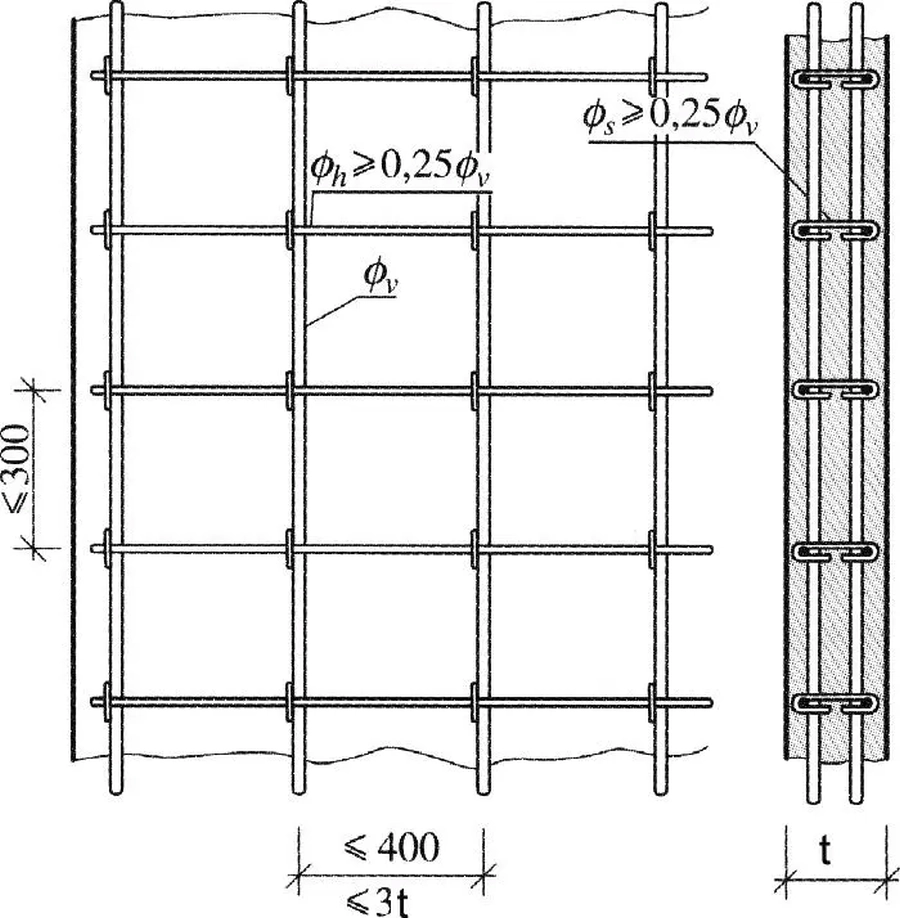
Minimalne i maksymalne zbrojenie i rozstaw prętów
Zbrojenie pionowe powinna mieć pole przekroju $A_{s,v} $:
$$\begin{equation} A_{s, v, min} =0,002 \cdot A_c \label{As_min} \end{equation}$$
$$\begin{equation} A_{s,v, max} =0,04 \cdot A_c \label{As_max} \end{equation}$$
Przyjmuje się, że zbrojenie pionowe i poziome ścian i tracz powinno być rozmieszczone po połowie przy każdej powierzchni bocznej. Zalecenie to musi być realizowane wówczas gdy stosuje się zbrojenie minimalne. Natomiast w przypadku wyznaczenia potrzebnego zbrojenia z modelu powłokowego ( również zginanie) można stosować zbrojenie niesymetryczne.
Rozstaw prętów pionowych $s_v$ powinien spełniać warunek
$$\begin{equation} s_v \le 400 \, mm \quad i \quad s_v \le 3\cdot t \label{s_v} \end{equation}$$
gdzie t- jest grubością ściany lub tarczy
Przy każdej powierzchni bocznej należy umieścić zbrojenie poziome (poprzeczne) o polu przekroju
$$\begin{equation} A_{s,h} \ge min [ 0,001 A_c \, ; \, 0,25 \cdot A_{s,v} ] \end{equation}$$
Rozstaw prętów poziomych $s_h$ powinien spełniać warunek
$$\begin{equation} s_h \le 300 \, mm \label{s_h} \end{equation}$$
W tej części ścian, w której stopień zbrojenia przekracza 2%, należy stosować strzemiona spełniające wymagania takie jak dla słupów.
Jeśli zbrojenie główne (najczęściej pionowe) jest umieszczone przy powierzchni ściany (bliżej niż zbrojenie poprzeczne), to należy stosować „spinki” – łączniki obu zbrojeń głównych przy powierzchniach ściany, w ilości nie mniejszej niż 4 łączniki na 1 m2. Jeżeli stosuje się siatki spajane z prętów o średnicy $∅ \le 16 \, mm$ i otulina zbrojenia jest nie większa niż 2∅ , to można nie stosować spinek.
Zbrojenie ścian i tarcz
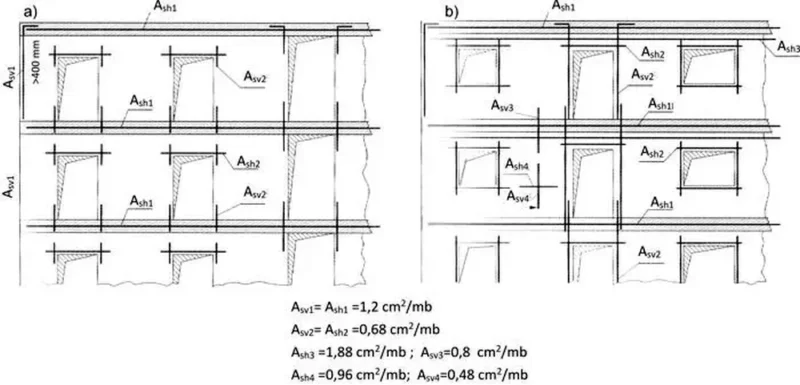
Na rys. 2 zilustrowano zasady zbrojenia głównego i poprzecznego ścian, opisane w ustępie wyżej
Rys.2 Zbrojenie ścian (opis w tekście) [1], rys. 11.8a
Krawędzie swobodne ścian należy wyposażyć w klamry i szpilki U (rys.3.)
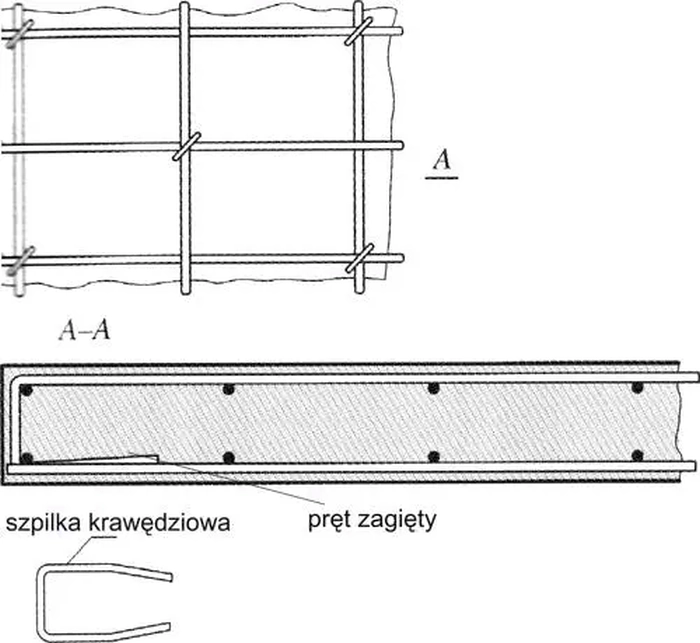
Rys 3 Obróbka krawędzi swobodnych ścian (na podstawie [1], rys.11.10)
Wybrane szczegóły zbrojenia naroży ścian zilustrowano na rys.4
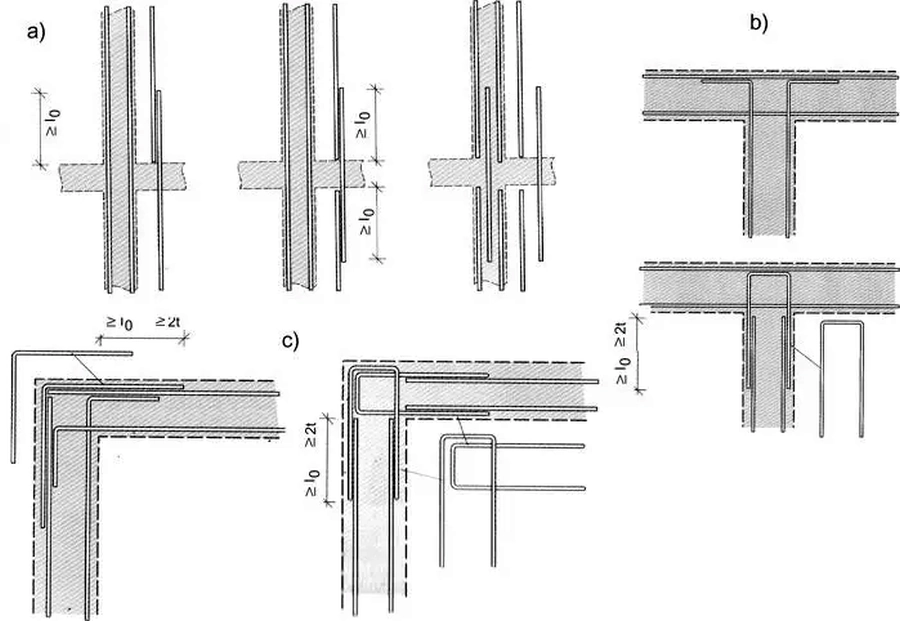
Rys,4, Detale zbrojenia naroży ścian: a) ścian a strop pośredni, b)ściana a strop górny, c) naroże poziome ( na podstawie [1])
Zbrojenie w narożach otworów
Zbrojeni wokół otworów w ścianach i tarczach, a szczególnie zbrojenie nadproży – historycznie było objęte szeregiem zaleceń, które należy wiązać z ręcznym obliczaniem ścian i tarcz. Współcześnie zalecenia te straciły na aktualności, bowiem wymagane zbrojenie jest wynikiem obliczeń numerycznych. Nie ma potrzeby dodatkowego dozbrajania naroży otworów, ale także nadproży, słupków i belek fundamentowych ponad zbrojenie wymagane obliczeniami.
Wyjątkiem są elementy słabo zbrojone i betonowe dla których należy dać minimalne zbrojenie konstrukcyjne (rys.5.)
Rys.5 Zbrojenie konstrukcyjne wokół otworów: a) ściana wewnętrzna, b) ściana zewnętrzna
Wymagania pożarowe dla ścian
Jeśli ściana stanowi oddzielenie pożarowe i powinna być odporna na uderzenia, to jej grubość nie powinna być mniejsza niż:
120 mm gdy ściana zbrojona i nienośna
140 mm gdy ściana zbrojona i nośna
200 mm gdy ściana jest niezbrojona
Otuleni osiowe zbrojenia w ścianach zbrojonych nie powinno byc mniejsze niż 25 mm ($a \ge 25 \, mm)
Warunki pożarowe ograniczają smukłość ścian do $\lambda_{max}=40$
Wymagania pożarowe dla ścian podano w tab.1. Współczynnik #\mu_{Fi}$ jest stopniem obciążenia ściany siła osiową (stosunek obliczeniowej siły podłużnej w sytuacji pożarowej do obliczeniowej siły granicznej w temperaturze normalnej)
Tab.1. Wymagania pożarowe dla ścian wg [2]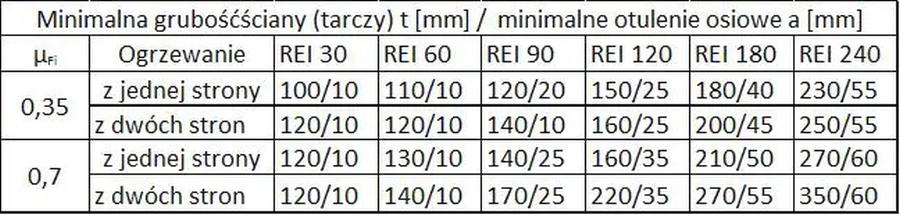
Modele kratownicowe w zbrojeniu tarcz
Model kratownicowy w obliczaniu i zbrojeniu tarcz, za w szczególności: ścian-belek, stref docisku, krótkich wsporników, podcięć belek i innych nieciągłości może być zawsze stosowany, ale współcześnie wobec dokładnego modelu obliczeniowego MES stracił na znaczeniu.
W wielu przypadkach miejscowo należy stosować zbrojenie sztywne (kształtowniki stalowe) , co umożliwia ograniczenie ugięć, ale także przejęcie znacznych naprężeń w miejscach nieciągłości.Literatura
- Starosolski W. (2013). Konstrukcje żelbetowe według Eurokodu 2 i norm związanych, Tom 3. Wydawnictwo Naukowe PWN
- PN-EN 1992-2+AC+Ap1+Ap2:2008, Projektowanie konstrukcji z betonu, Część 1-2: Reguły ogólne – Projektowanie z uwagi na warunki pożarowe
________________________________
