A B C D E F G H I K Ł M N O P R S T U W Z

Pa Pe Pi Pl Pł Po Pr

Prę Pro Prz

Przeb Przek Przew

Przewody elektroenergetyczne i kolei linowych

Przewody napowietrznych linii elektroenergetycznych oraz kolei linowych są wyposażone w przewody – liny rozciągnięte pomiędzy słupami. Długość tych przewodów (odległość podpór) może dochodzić do kilku kilometrów. Obciążenie i nieliniowości konstrukcji są znaczne i wymagają dokładnych oraz żmudnych, zaawansowanych analiz.

Spis treści ukryj

1 Wprowadzenie

2 Statyka lin- przewodów

2.1 Równanie stanu liny- przewodu

2.2 Obciążania klimatyczne liny- przewodu

2.2.1 Obciążenie oblodzeniem

2.2.2 Kombinacje obciążeń klimatycznych lin-przewodów

2.2.3 Podziel się:

2.2.4 Like this:

2.2.5 Podobne artykuły

Wprowadzenie

Na rys. 1 pokazano przykład realizacji lin nośnych górskiej kolejki linowej, a na rys.2 przykład linii elektroenergetycznej ponad rzeką Łabą.

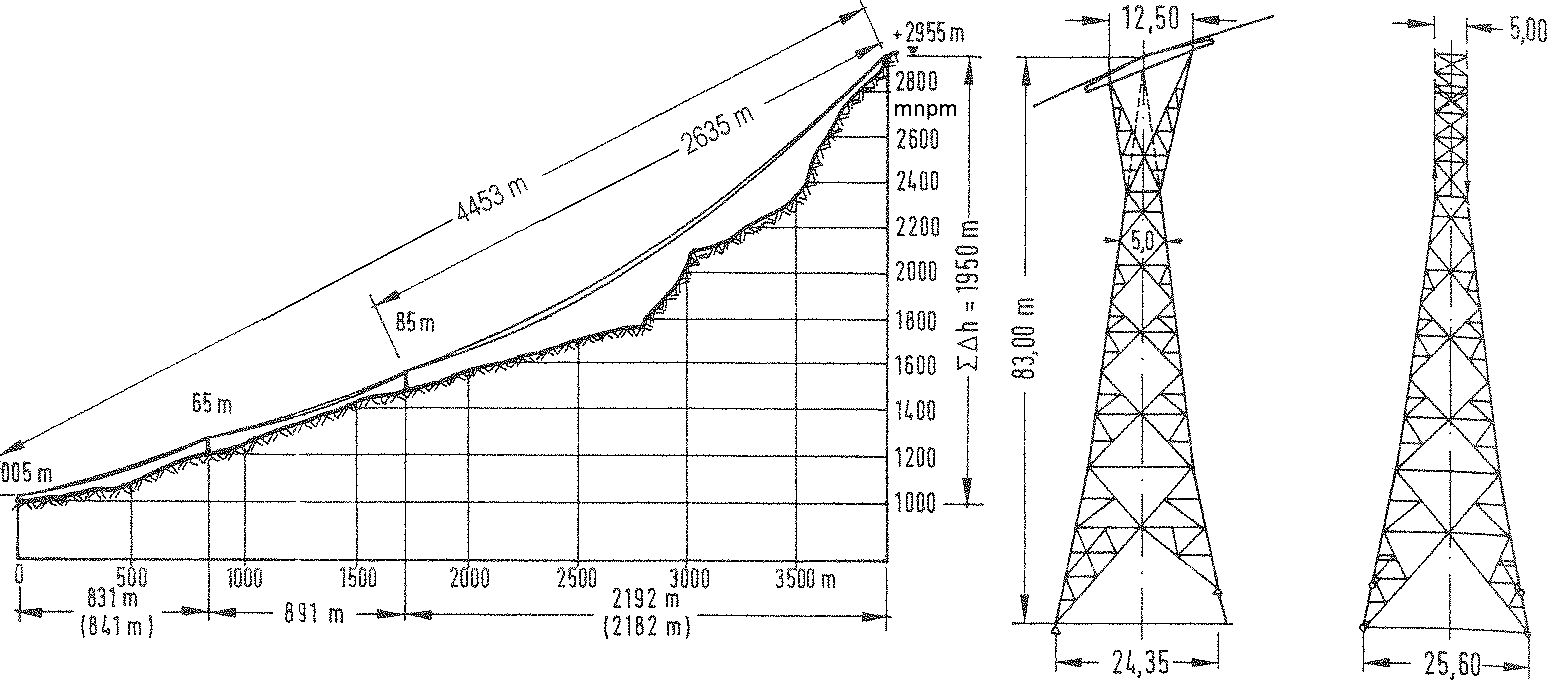Rys.1. Przewody kolei linowej [1]– str. 866

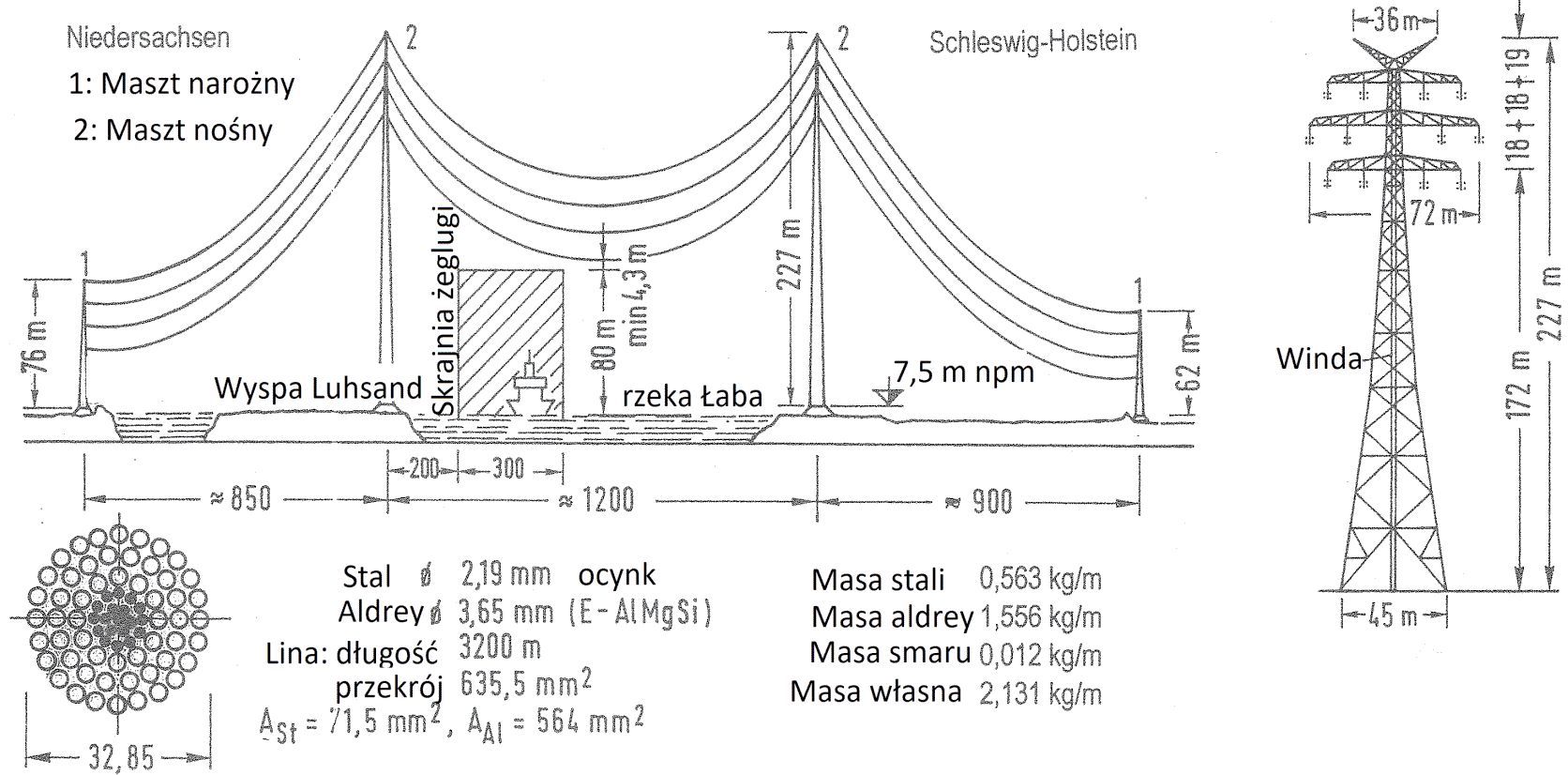Rys.2. Przewody elektroenergetyczne [1]– str. 854

W każdym przypadku przewody elektroenergetyczne lub kolei linowych charakteryzują się dużymi rozpiętościami i zwisami.

Statyka lin- przewodów

Równanie stanu liny- przewodu

W artykule Statyka cięgna omówiono statykę pojedynczej liny lub kolei lub przewodu, rozpiętego pomiędzy dwiema podporami A i B. Pokazano, że cięgno układa się w krzywą łańcuchową w sposób przedstawiony na rys. 2, które można opisać formułą:

$y=\dfrac{H}{q}\cdot cosh \dfrac{x}{H/q}$ ,

(1)

gdzie: q- obciążenie liniowe cięgna, H – rozciąg cięgna (reakcja pozioma) (rys.3).

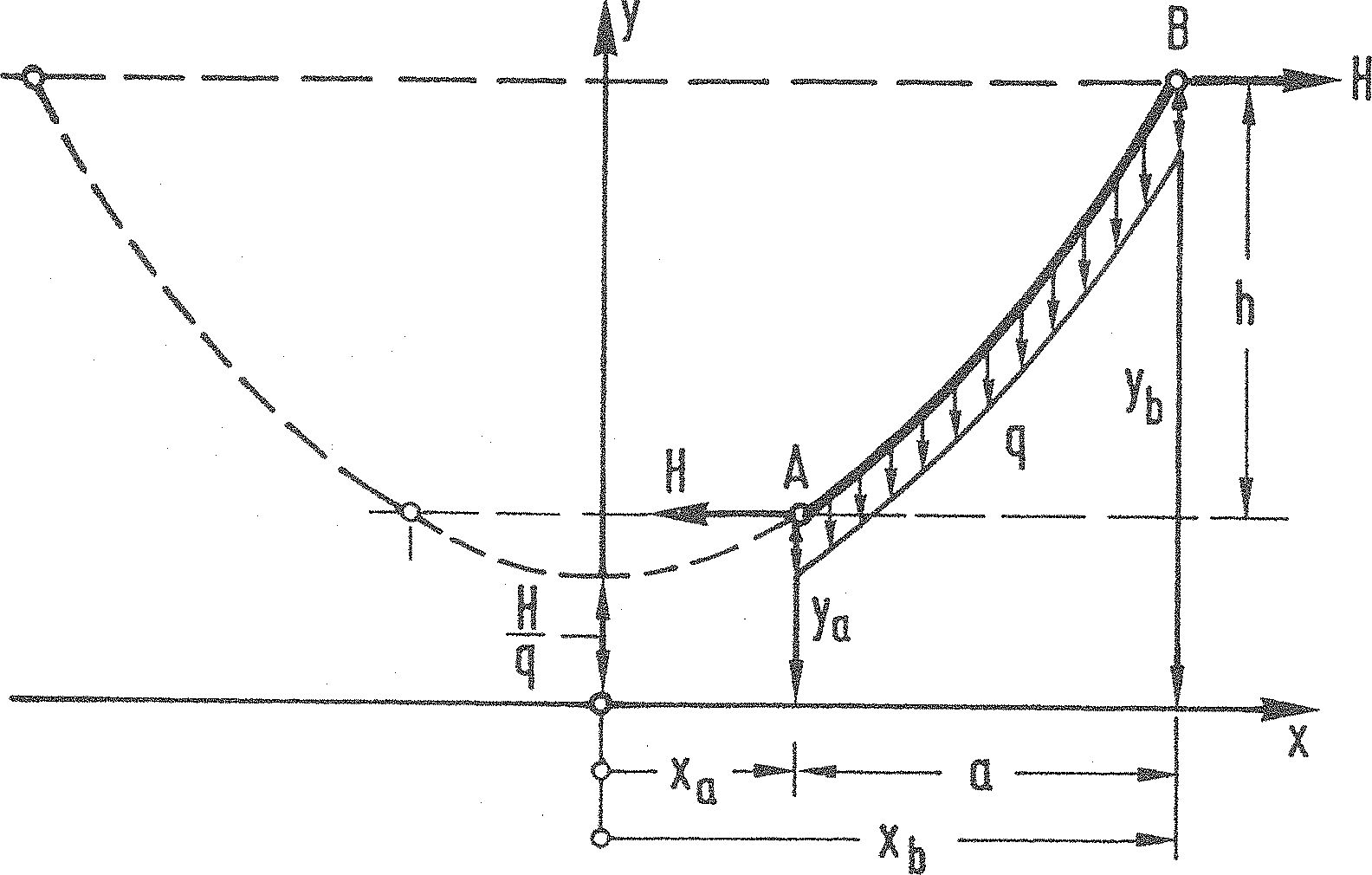Rys.3. Pojedyncza lina (przewód) rozpięty pomiędzy punktami A i B [1]– str. 852

Dla odcinka cięgna rozpiętego pomiędzy punktami o różnicy w poziomie $a$ i poziomów $h$ dla rzędnych punktów zawieszenia $A(x_a, y_a)$ , $B(x_b, y_b)$ , korzystając z własności funkcji hiperbolicznych, linię cięgna można zapisać w postaci [1]– str. 852:

$y=\dfrac{H}{q}\cdot \left ( cosh \dfrac{x_b}{H/q}- cosh \dfrac{x_a}{H/q}\right )=\dfrac{2H}{q}\cdot sinh \dfrac{x_b+x_a}{2H/q}\cdot sinh \dfrac{x_b-x_a}{2H/q}$

$=\dfrac{2H}{q}\cdot sinh \dfrac{a}{2H/q}\cdot sinh \dfrac{a+2x_a}{2H/q}$ ,

(2)

gdzie:

$x_a=\dfrac{H}{q}\cdot aec sinh \left( \dfrac{h}{2H/q} \cdot \dfrac{1}{sinh \dfrac{a}{2H/q}} \right)-\dfrac{a}{2}$ ,

(3)

Tutaj $x_a$ jest dodatnią odległością podpdory a od osi $y$ . Obciążenie q jest złożone z: ciężaru własnego $g$ , zwykłych obciążeń zimowych (szron, lód, śnieg), dodatkowych obciążeń (zależnych od szczególnych danych meteorologicznych i topograficznych) oraz wiatru. Obciążenia termiczne rozpatruje się dla temperatury otoczenia (-20, -5, 5 , +10°C ). Należy stosować odpowiednie kombinacje obciążeń ze współczynnikami redukcyjnymi (jednoczesności).

Równanie stanu cięgna (35) z artykułu Statyka cięgna dla przewodów i lin można zapisać w postaci [1]– str. 853:

$\sigma_1^3 + \left [\dfrac{E \gamma_2^2 a^2}{24 \sigma_2^2} -E \cdot \alpha_t \cdot (t_2-t_1) -\sigma_2\right ]\cdot \sigma_1^2 – \dfrac{E\gamma_1^2 a^2}{24}$ ,

(4)

gdzie przyjęto oznaczenia opisane w artykule Statyka cięgna.

Obciążania klimatyczne liny- przewodu

Obciążenie oblodzeniem

W normie [2] wskazano, że obciążenie oblodzeniem można przyjmować przy założeniu, że element konstrukcyjny jest pokryty taką samą grubością lodu na całej powierzchni (rys. 3).

Rys. 3 Grubość oblodzenia elementów konstrukcyjnych [2]

Wartości obciążenia oblodzeniem przyjmować zgodnie z normami: [2], [3].

Głównymi warunkami przyrostu lodu są wymiary odsłoniętego obiektu i jego orientacja na kierunek wiatru lodowcowego. Oblodzenie atmosferyczne jest tradycyjnie klasyfikowane według dwóch różnych procesów : a) oblodzenia od opadów; b) oblodzenie w chmurze. Na rys.4. pokazano główne parametry tworzącego się się lodu. Gęstość lodu waha się w szerokim zakresie od miękkiego lodu poprzez średni ciężkiego (glazury).

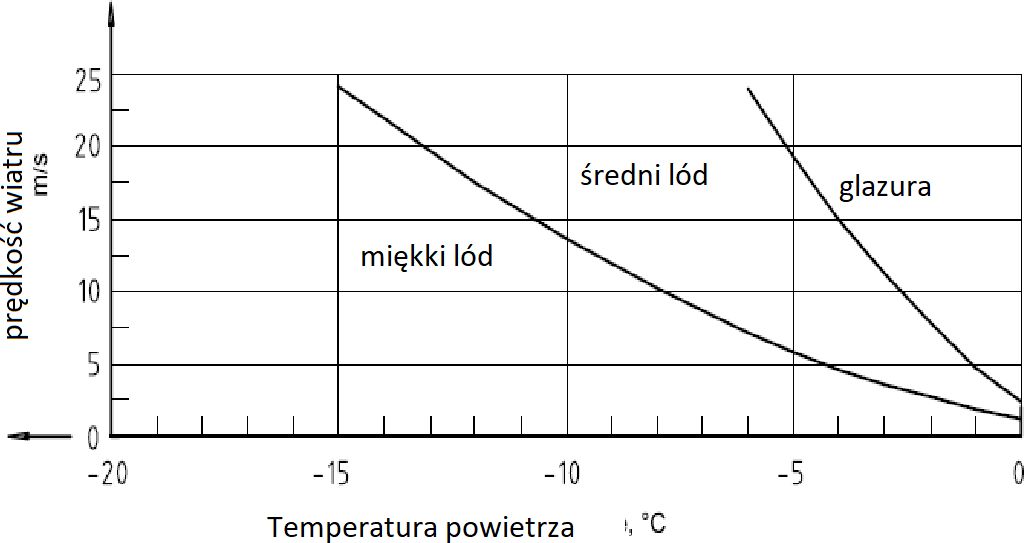Rys.4 Czynniki warunkujące rodzaj lodu [2], [3]

Masa lodu na konstrukcji może się znacznie różnić w zależności od wysokości elementu nad terenem, ale do tej pory niestety nie znaleziono nie znaleziono rozkładu lodu z wysokością. W niektórych przypadkach lód może nie być obserwowany w pobliżu poziomu gruntu, ale na wyższych poziomach obciążenie lodowe może być znaczące.

Masa właściwa poszczególnych rodzajów lodu wynosi [2], [3]:

glazura (symbol ICG) $900 \, kg/m^3$ i przyjmuje się w klasach grubości od t=10mm (klasa G1) do t=50mm (klasa G5) i więcej (klasa G6),
średni lód (symbol ICR) $300 \quad do \quad 900 \, kg/m^3$

W pracy [1] – str. 852 podano, że zwykle obciążenie zimowe (oblodzenie) $L$ przyjmuje się jako

$L=(5+0,1d) [ N/m ] ( d [mm] )$ ,

(5)

Odpowiada to w przybliżeniu średniej grubości lodu ciężkiego (glazury) wg normy [2] , [3]. Ze względu na nieprecyzyjne uregulowania w tej normie w projektowaniu konstrukcji budowlanych zwykle przyjmuje się wg formuły (5), które w przypadku dużych wysokości nad poziomem morza jest zwiększane zgodnie z danymi lokalnymi.

Kombinacje obciążeń klimatycznych lin-przewodów

Obciążenia zimowe, wiatr i temperaturę przykłada się z uwzględnieniem jednoczesności ich działania:

przy -20°C bez obciążeń zimowych i bez wiatru,
przy -5°C ze zwykłymi obciążeniami zimowymi w kombinacji z wiatrem,
przy +5°C z wiatrem, bez obciążeń zimowych,
$t_{max}$ =+ 40°C

Wymienione wyżej temperatury zastały tak dobrane, ponieważ z badań wynika, że w mroźnym powietrzu (-20°C) jest zbyt mała wilgotność, by mógł wytwarzać się lód lub sadź. Optymalną temperaturą do tworzenia sadzi i lodu jest ok -5°C. Lód natomiast nie tworzy się w dodatnich temperaturach.

W normie podano współczynniki redukcyjne (kombinacji wiatr-lód (W-L), gdy jedno z nich jest wiodące – wówczas towarzyszące redukuje się o połowę ( $\psi_W=\psi_L=0,5$ ), czyli będziemy mieli W+0,5L lub L+0,5W.

Współczynniki obciążeń zależą od klasy niezawodności: klasa 3 niezawodności dotyczy obiektów w miastach i konstrukcji, których konsekwencje zniszczenia mogą być bardzo poważne; klasa 2 dotyczy wszystkich obiektów, które nie są zakwalifikowane do klasy 1 lub 3 ; Klasa 1 dotyczy mało zaludnionych otwartych terenów wiejskich i obiektów o małym prawdopodobieństwie strat w ludziach. Współczynniki obciążeń $\gamma_f$ wynoszą:

do obciążeń stałych $\gamma_G = 1,2; 1,1; 1,0$ – dla klasy niezawodności 3, 2 i 1 odpowiednio ,
do obciążeń zmiennych $\gamma_Q = 1,6; 1,4; 1,2$ – dla klasy niezawodności 3, 2 i 1 odpowiednio.

Zgodnie z normą do projektowania przewodów elektroenergetycznych [4] obliczenia przewodów należałoby prowadzić dla następujących kombinacji obciążeń:

$1,0L + 0,4 W$ ,
$0,35L+0,7 W$ ,
$1,0 W$ ,
$1,0 L$ .

Zdaniem autora kombinacje należy ustalać w sposób spójny z Eurokodem jak opisano wyżej, to jest dla nieco większych obciążeń kombinacyjnych niż przewiduje [5].

Literatura

Petersen C., (2013), Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten, 4 Wydanie
PN-EN 1993-3-1+AC+Ap1: 2008, Eurokod 3: Projektowanie konstrukcji stalowych – Część 3-1: Wieże, maszty i kominy- Wieże i maszty
ISO 12494:2001, Atmospheric icing of structures
PN-EN 50341-1-2 2 :2010
PN-EN 50341-3-22:2010, Elektroenergetyczne linie napowietrzne prądu przemiennego powyżej 45 kV – Część 3: Zbiór normatywnych warunków krajowych

________________________________

Podobne artykuły

15 paź 16

By : Leszek Chodor

Comments : 0

O autorze

* dr inż. Leszek Chodor. Architekt i Inżynier Konstruktor; Rzeczoznawca budowlany. Autor wielu projektów budowli, w tym nagrodzonych w konkursach krajowych i zagranicznych, a między innymi: projektu wykonawczego konstrukcji budynku głównego Centrum "Manufaktura" w Łodzi, projektu budowlanego konstrukcji budynku PSE w Konstancinie Bielawa, projektów konstrukcji "Cersanit" ( Starachowice, Wałbrzych, Nowograd Wołyński-Ukraina), projektu konstrukcji hali widowiskowo-sportowej Arena Szczecin Autor kilkudziesięciu prac naukowych z zakresu teorii konstrukcji budowlanych, architektury oraz platformy BIM w projektowaniu.