Powierzchnie o powierzchniach postokreśłnych (prostoliniowych) są ważną klasą powierzchni, znajdującą wiele zastosowań w technice, architekturze i budownictwie. Przekrycia zbudowane z takich powierzchni są wynikiem ruchów linii prostej (prostej tworzącej) po krzywej kierującej. Kierującą może być linia śrubowa (pkt.2), proste skośne (pkt. 3), proste równoległe do zadanej płaszczyzny (pkt.4), itd.
Powierzchnia prostokreślna
Powierzchnia jest prostokreślna (rozwijająca, prostoliniowa), jeżeli ma parametryzację postaci
$ x(u,v)=\beta (u)+v\delta (u)\$,
gdzie $\beta$ i $\delta$ są krzywymi.
Cała powierzchnia jest zbudowana z prostych wychodzących z krzywej $\beta(u)$ w kierunku $\delta(u)$. Krzywa $\beta(u)$ jest nazywana kierownicą (kierującą), natomiast prosta o kierunku $\delta(u)$, to tworząca.
Na rys. 1 pokazano przykazano model fizyczny wybranej powierzchni prostokreślnej.

Rys.1. Model powierzchni postokreślnej
[Wikipedia]
Powierzchnie śrubowe
Powierzchnia śrubowa jest spotykana codziennie, przede wszystkim w gwintach śrub. Sposób tworzenia powierzchni śrubowej pokazano na rys.1. Powierzchnię śrubową prostoliniową, otwartą, której kierująca jest linia śrubowa $”1-7″$, leżąca na powierzchni walca obrotowego o promieniu $r$ i osi pionowej $”l”$, otrzymujemy jako zbiór prostych stycznych $ t_1, t_2,…t_n $ – tworzących linii śrubowej $\Theta$.
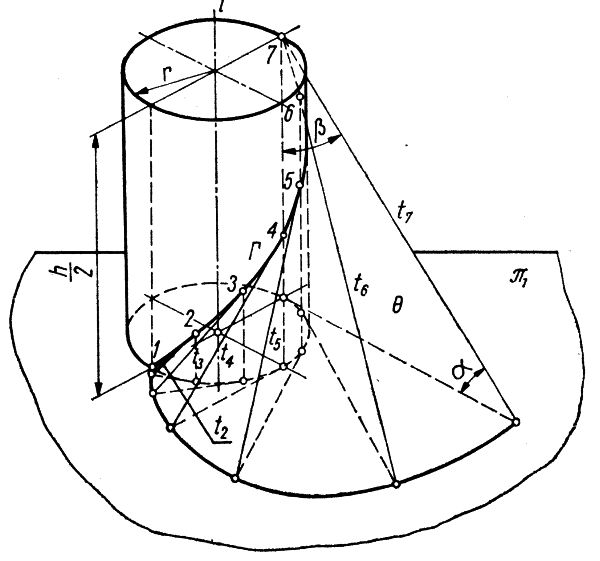
Rys.1.Sposób tworzenia powierzchni śrubowej prostoliniowej, rozwijalnej [1]
Utworzony na rys.1 płat powierzchni jest jednym z dwóch płatów powierzchni ewolwentowej, dla której kierująca $\Gamma$ jest krawędzią zwrotu (rys.2) i która należy do powierzchni prostoliniowych rozwijalnych – przy rozwinięciu na płaszczyznę linia śrubowa”1-7″ staje się krzywą płaską (skręcenie równe zero) o tej samej krzywiźnie.. Taka krzywa jest tylko jedna – okrąg o promieniu równym promieniowi krzywizny krzywej. To znaczy po rozwinięciu powierzchni śrubowej nas płaszczyznę, łuk linii śrubowej $\Gamma$ staje się łukiem okręgu, a powierzchnia rozwijalna nakłada się na tę część płaszczyzny , która znajduje się na zewnątrz okręgu, pokrywając go dwukrotnie [1].
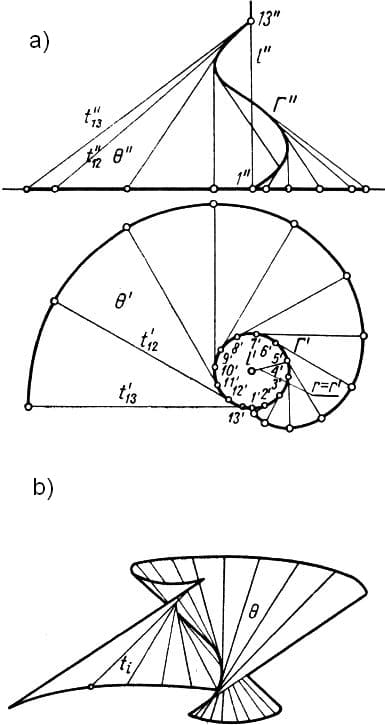
Rys.2. Powierzchnia śrubowa, prostoliniowa, rozwijalna: a) rzuty, b) model $\Theta$
Na rys. 3 przedstawiono dwa rzuty powierzchni śrubowej $\Theta$ ograniczonej współosiową powierzchnią walca obrotowego o promieniu R>r, to znaczy w przypadku, gdy powierzchnia walcowa przenika powierzchnię śrubową po linii śrubowej o tym samym skoku , jaki przyjęto dla kierującej $|Gamma$.
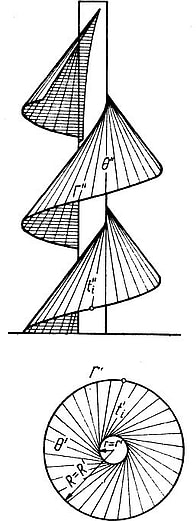
Rys.3. Powierzchnia śrubowa, prostoliniowa, rozwijalna ograniczona współosiowym walcem: a) rzuty, b) model $\Theta$
Jeżeli tworząca $t$ jest prosta przecinająca o pod kątem prostym, to powstaje powierzchnia, którą nazywamy zwyczajną powierzchnią śrubową. Powierzchnia śrubiowa zwyczajna jest powierzchnią minimalną (rys.4)
Rys.4. Powierzchnia śrubowa, prostoliniowa, rozwijalna – zwyczajna $\Theta$
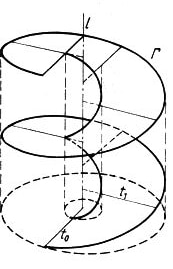
W wyniku ruchu dowolnej prostej (poza przypadkiem rys.3) powstaje prostoliniowa powierzchnia śrubowa o sąsiednich tworzących ukośnych, a więc powierzchnia nierozwijalna. Na rys. 5 pokazano przykładową powierzchnię śrubową nierozwijalną ograniczoną dwiema liniami śrubowymi walcowymi $|Gamma_1$ i $\Gamma_2$
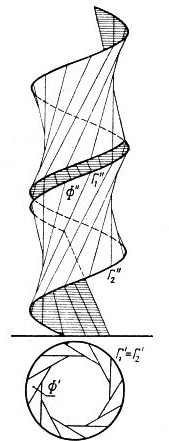
Rys.5. Powierzchnia śrubowa, prostoliniowa, nierozwijalna, ograniczona współosiowymi walcami $\Theta$
Płaty powierzchni śrubowych, przedstawione na rys. 3 i 5 mogą stanowić podstawę geometryczną kształtowania przekryć o pojedynczej i podwójnej krzywiźnie.
Kwadryki z dwiema liniami podwójnymi
Kwadryki z dwiema podwójnymi liniami jest walcem ukośnym z dwiema kierującymi, pokazanym na rys.6
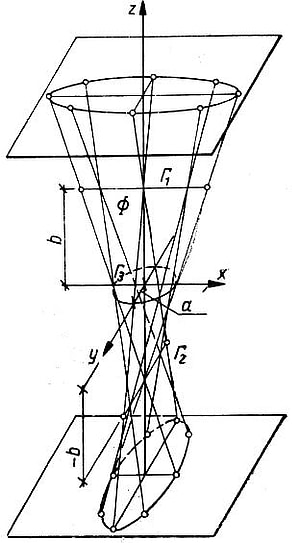
Rys.6. Model kwadryki z liniami podwójnymi
Kierującymi są dwie proste: $|Gamma_1$ i $\Gamma_2$, z których jedna zwykle jest prostą pionową , oraz krzywa $\Gamma_3$ – najczęściej okrąg, parabola lub hiperbola. Jest to powierzchnia algebraiczna czwartego stopnia. Zwykle interesuje nas nie cała krzywa, lecz jej płat. Na rys. 7 pokazano konstrukcję płata kwadryki z dwiema liniami podwójnymi, w której: $\Gamma_1$- prosta pozioma, $\Gamma_2$- prosta pionowa, $\Gamma_3$- półokrąg, leżący w płaszczyźnie pionowej równoległej do $\Gamma_1$.
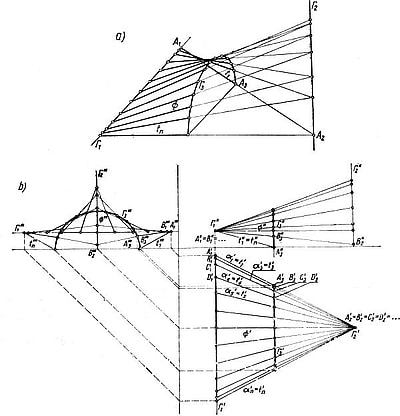
Rys.7. Płat kwadryki z dwiema liniami podwójnymi, rozpięty nad trapezowym rzutem: a) aksonomteria, b) rzuty
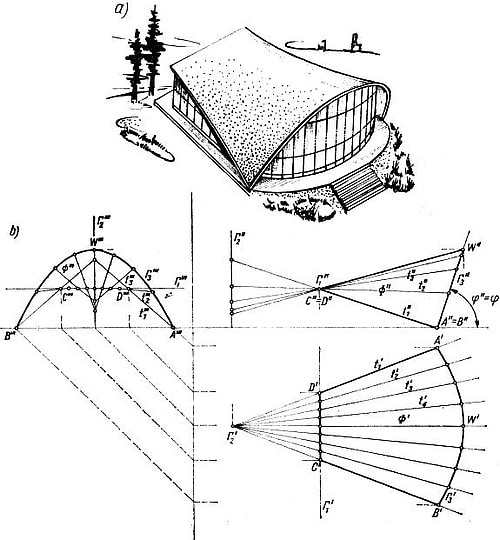
Rys.8. Projekt przekrycia z płatem kwadryki z dwiema liniami podwójnymi: a) widok obiektu, b) konstrukcja kwadryki
Powierzchnie Catalana
Największe zastosowanie w konstrukcjach przekryć dachowych spośród powierzchni prostoliniowych znajdują powierzchnie z grupy powierzchni Catalana, a wśród nich: cylindroidy, konoidy, paraboloidy , hiperboloidy (patrz również artykuł: kopuły siatkowe). Wybrane powierzchnie Caralana pokazano na rys.10.
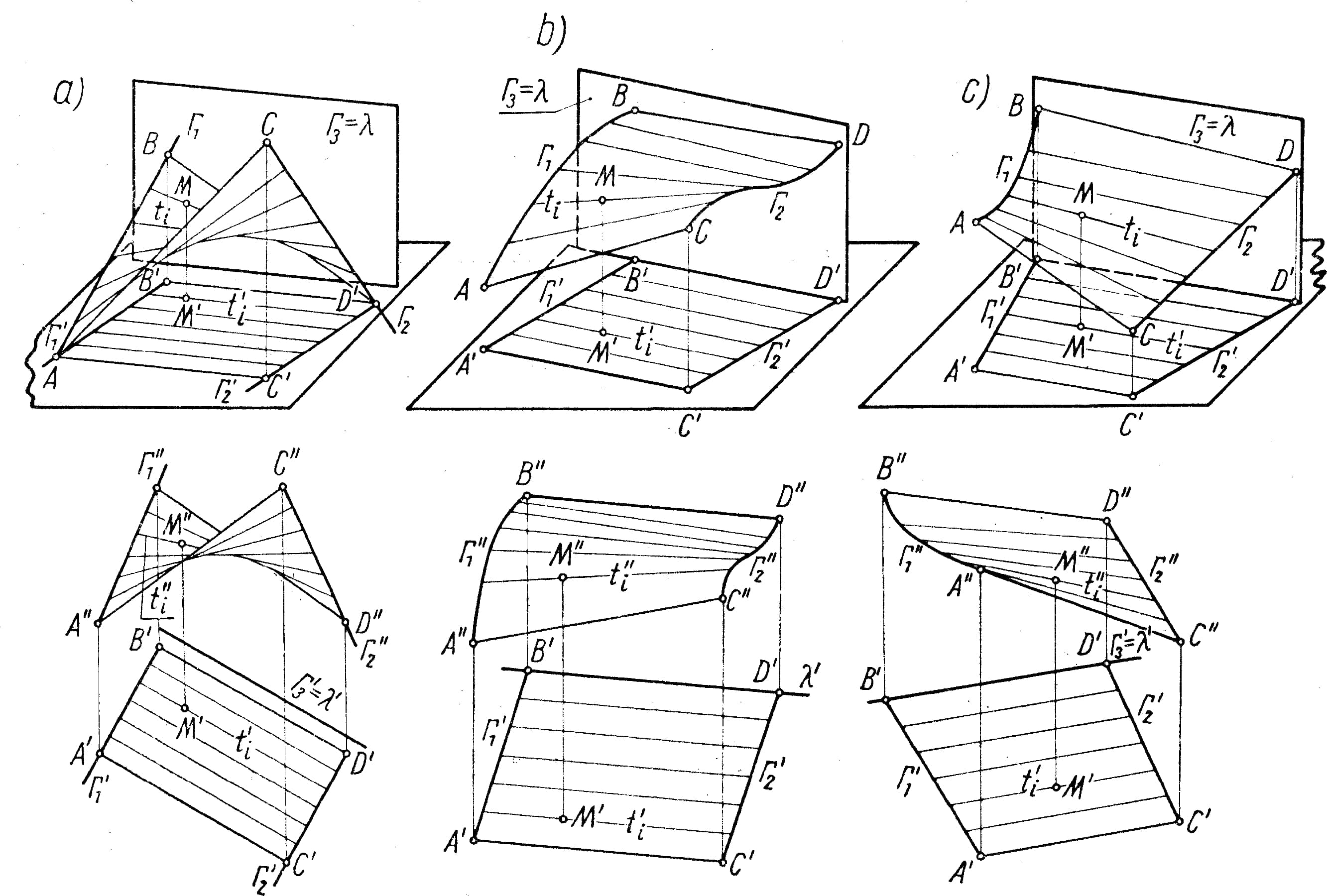
Rys.10 Powierzchnie Catalana: a) hypar (paraboloida hiperboliczna), b)cykloida, c) konoida
Na rys. 11 do 16 pokazano przykłady konstrukcji powierzchni Catalana dla rozmaitych tworzących i kierujących, a na rys. 17 przykład projektu przekrycia z powierzchni prostoliniowych.
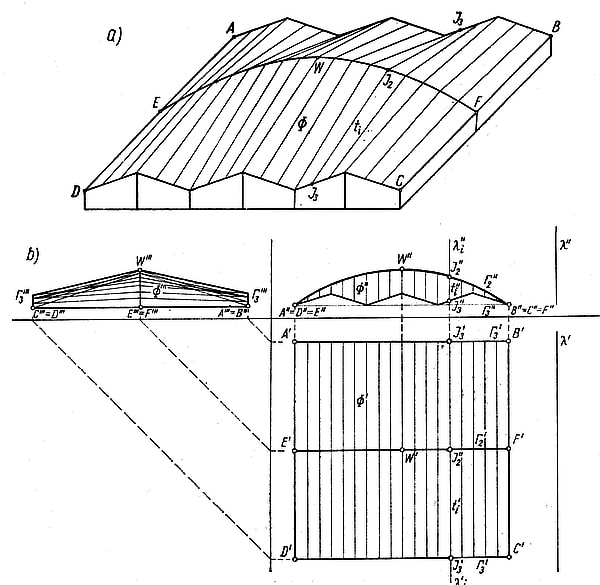
Rys.11. Przekrycie, którego linią brzegową jest linia łamana: a) aksonometria, b) rzuty
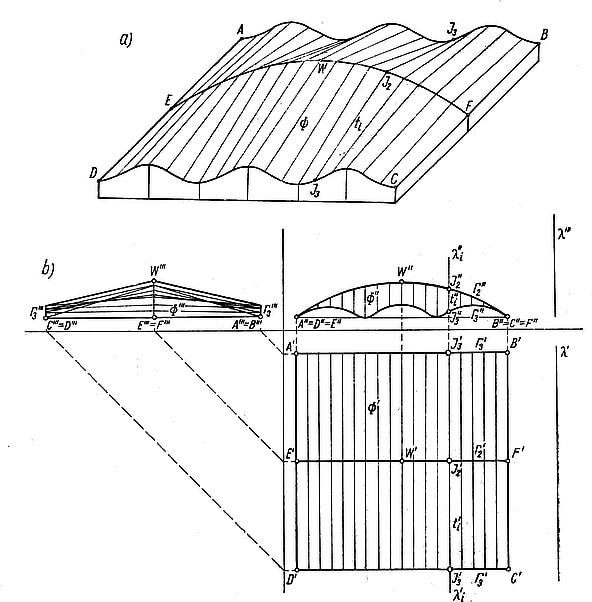
Rys.12. Przekrycie, którego linią brzegową jest linia krzywa- sinusoida: a) aksonometria, b) rzuty
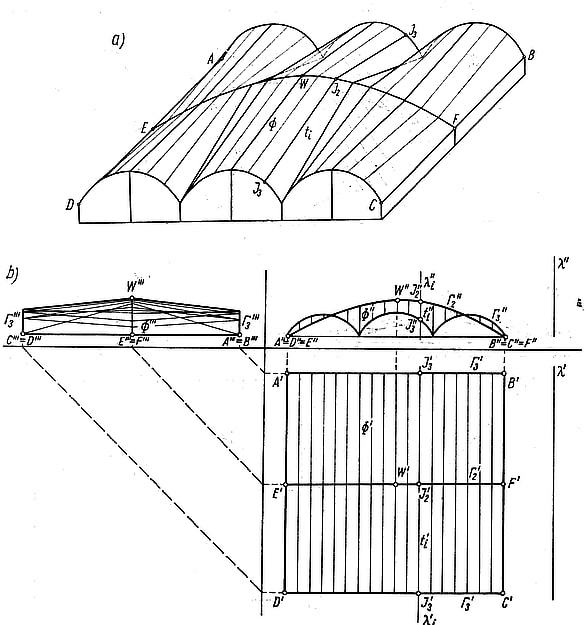
Rys.13. Przekrycie, którego linią brzegową są łuki cykloidy: a) aksonometria, b) rzuty
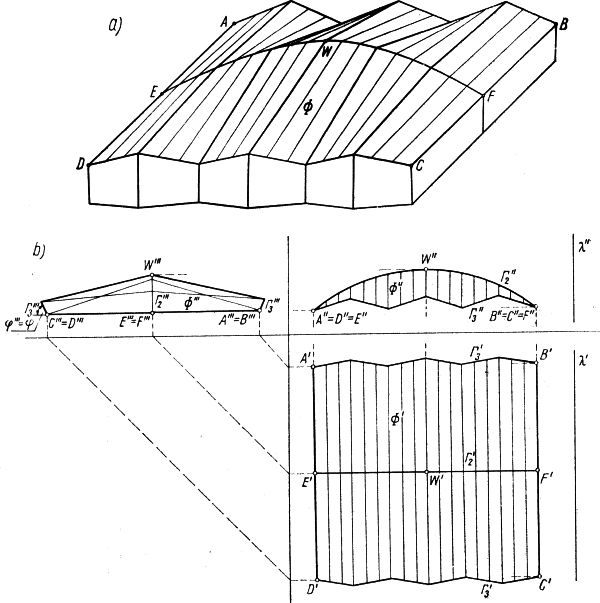
Rys.14. Przekrycie, ograniczone łukiem paraboli : a) aksonometria, b) rzuty
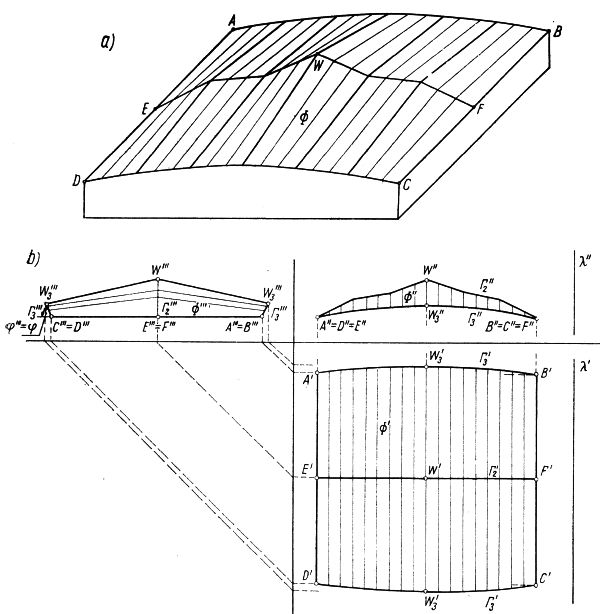
Rys.15. Przekrycie, którego linie brzegowe (parabole) nie leżą w płaszczyznach pionowych : a) aksonometria, b) rzuty
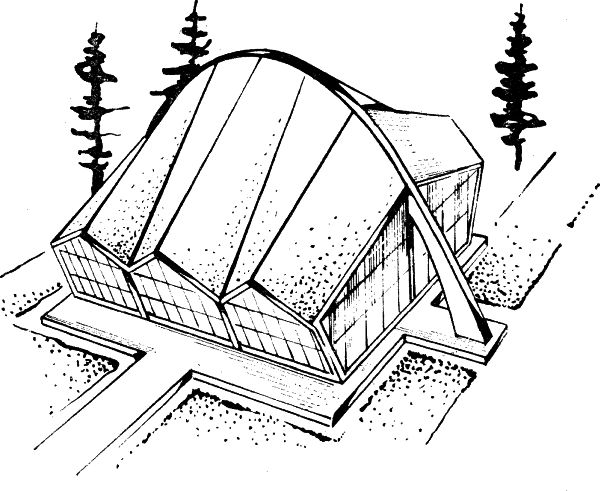
Rys.16. Projekt przekrycia utworzony przez ruch linii prostej stale równoległej do zadanej płaszczyzny pionowej, ślizgającej się po paraboli leżącej w płaszczyźnie symetrii i po liniach łamanych, będących jednocześnie liniami brzegowymi
Inne powierzchnie prostokreślne
Powierzchnie prostoliniowe często należy rozpiąć na innymi rzutami od pokazanych w poprzednich rozdziałach. Dokonuje się tego, bazując na rozwiązaniach dla płatów podstawowych, następnie skleja, przycina itd. Na rys. 18 pokazano przykładowo przekrycie rozpięte nad gwiaździstym rzutem poziomym.
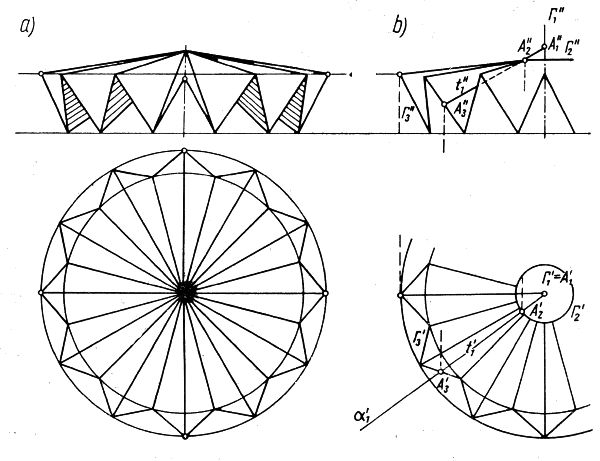
Rys.17. Powierzchnia prostoliniowa nad kołowym (gwiaździstym) rzutem; a) przekrycie utworzone z elementów płaskich, b) konstrukcja zmierzająca do utworzenia kwadryki z dwiema liniami podwójnymi
Rysunki 1 do 17 zaczerpnieto z pracy [1].
Literatura
- Przewlocki S., (1970), Przekrycia dwukrzywiznowe. Zasady kształtowania geometrycznego, Arkady, Warszawa
________________________________




