Przebicie płyty żelbetowej

Leszek Chodor,  21 czerwca 2018

Artykuł w ciągu ostatnich 24 godzin czytało 19 Czytelników

Przebicie  płyty żelbetowej to ścinanie płyty wokół podpory lub na obwodzie zamkniętym wokół  znacznej siły skupionej (faktycznie rozłożonej na małym obszarze).  Przebijanie przez ścinanie (ang. punching shear) jest analizowane jak standardowe ścinanie żelbetu, a specyfiką zjawiska   jest dobór obwodu ścinania, zależnie od kształtu obszaru siły ścinającej (przebijającej- niszczącej), jej lokalizacji na powierzchni płycie, w szczególności w pobliżu krawędzi płyty, w tym  obok otworów w płycie. W modelu  normowym [1], wynikającym z licznych obserwacji i badań eksperymentalnych, np. [2], uwzględniono mimośrodowość przyłożenia siły skupionej, wynikającej z mimośrodu konstrukcyjnego (działania w podstawie/głowicy słupa  momentów zginających obok sił normalnych ) jak również imperfekcji geometrycznych. Zniszczenie stref płyty wokół słupów jest jednym z ważniejszych mechanizmów zniszczenia płyt żelbetowych fundamentowych, a także stropodachów. Płyty stropowe ze słupem górnej kondygnacji ustawionym nad  słupem dolnej kondygnacji, zwykle nie są narażone na zniszczenie przez przebicie.

Na rys. 1 pokazano jedną z pierwszych spektakularnych katastrof budowlanych płyty stropowej wskutek utraty nośności na ścinanie w obszarze przysłupowym.

Rys.1. Zniszczenie przez przebicie stropu Piper’s Row Park Car. Wolwerhampton 1975 (wybudowany 1965) [link do źródła]

Model zniszczenia  płyty ścinaniem przez przebicie

Zagadnienie teorii sprężystości o obciążeniu miejscowym płyty

Z rozwiązania podstawowego zadania teorii spręzytości = płyt o średniej grubości [3], dział XIII, otrzymujemy fundamentalny związek, leżący u podstaw teorii ścinania płyt żelbetowych przez przebicie. Na rys. 2 pokazano szkic modelu sprężytej płyty kołowej obciążonej  lokalnie centralnym obciążeniem zewnętrznym $q_E$ rozłożonym po obwodzie koła o  promieniu $c$. Suma obciążenia $q_E$ wynosi $V_E$. Płyta ma skończoną grubość $h$.

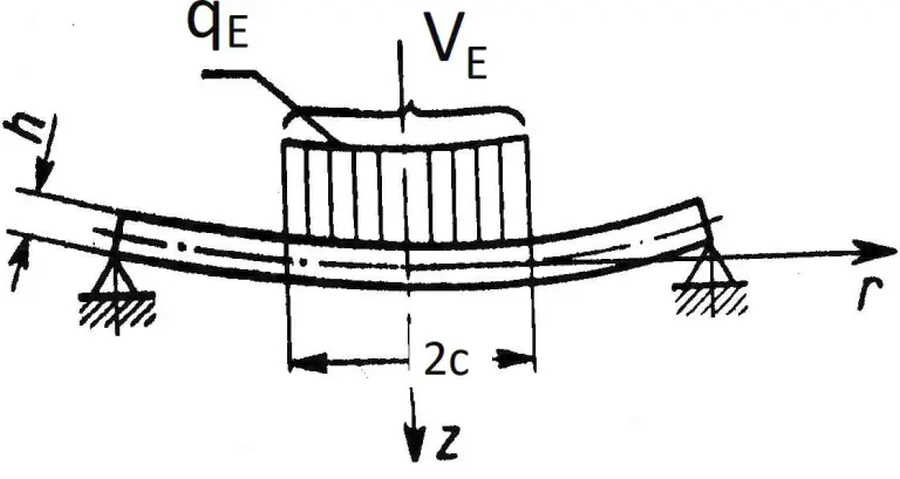
Rys.2 Schemat płyty o średniej grubości obciążonej miejscowo centralną siłą [3]

Dla takiego modelu możemy uzyskać prostą analityczną formułę na jednostkowe (przypadająca na jednostkę grubości) siły ścinające  $t$  w postaci  [3], wzór (30.0.11):

$$\begin{equation} t(r)= \dfrac {V_E}{2 \pi r }+\dfrac{1}{r} \int \limits_0^r \rho q_E (\rho) d\rho \label{1} \end{equation}$$

gdzie: r jest zmienną – współrzędną biegunową punku płyty, a $\rho$ jest  bieżącą zmienną całkowania- odległością od środka płyty.

Obciążenie $q_E$  jest przyłożone na obwodzie, co modeluje obciażenie krawędzią sztywnego stempla (słupa)  o promieniu Sc$.

W rozwiązaniu ($\ref{1}$)  nie występuje rozmiar płyty. Rozwiązanie jest słuszne dla płyty kołowej  o dowolnym promieniu $R> c$, średniej grubości, ale   obciążonej  idealnie wokół środka. W modelu z mimośrodami lub dla płyt o innym kształcie  rozwiązanie ścisłe jest trudne do uzyskania.

Po wykonaniu całkowania przypisanego w ($\ref{1}$)  otrzymujemy wyrażenia na natężenie sił poprzecznych w przekrojach płyty:

$$\begin{equation} t =\begin {cases}
\cfrac {q_E \cdot r}{2}. & \text { dla } r < c \textrm{ (wewnątrz obwodu obciążenia)} \\
\cfrac {q_E \cdot c^2}{2\cdot r}= \cfrac{V_E}{2\pi r}, & \text { dla } r \ge  c  \textrm{ (w obwodzie obciążenia i poza nim )} \\
\end {cases} \label{2}\end{equation}$$

Po podstawieniu do ($\ref{2}$b)  obwodu $u_x = 2 \pi  r_x$ x-tego przekroju  o promieniu $r_x$  oraz oznaczeniu $t=v\cdot d$,  gdzie $d$ – efektywna wysokość przekroju betonowego, $v$ – naprężenia styczne w przekroju, otrzymujemy fundamentalne rozwiązanie zagadnienia ścinania płyty przez przebicie:

$$\begin{equation}v_{Ed,x} = \cdot \dfrac{V_{Ed}}{u_x \cdot d}  \label{3} \end{equation}$$

Współczynnik nierównomierności β

Teoretycznie ścisła formuła ($\ref{3}$) na wywołane siłą obliczeniową $V_{Ed}$), naprężenia ścinające $v$ w x-tym przekroju, umiarkowanie oddalonym od powierzchni obciążeń uzyskane przy założeniu  braku mimośrodów, jest w Eurokod 2, korygowana współczynnikiem  mimośrodowości obciążenia  $\beta$ i zapisywana   w postaci.

$$\begin{equation}v_{Ed,x} = \beta \cdot \cfrac{V_{Ed}}{u_x \cdot d}  \label{4} \end{equation}$$

Współczynnik $\beta$ występujący w ($\ref{4} $), uwzględnia mimośrodowe przyłożenie obciążenia w stosunku do teoretycznej osi słupa (powierzchni obciążenia), a także inne odstępstwa od modelu teoretycznego rys.2, w tym kształtu słupa , kształtu  płyty,  ułożenia i kształtu innych podpór punktowych (słupy) , liniowych (ściany)  i innych warunków brzegowych.

Praktycznie  ważne i stosowane wartości współczynnika mimośrodów $\beta$ uzależnia się od lokalizacji słupa w sposób pokazany na rys. 3, przy  czym podane wartości $\beta$ są przybliżone i można je stosować, jeżeli poprzeczna stateczność konstrukcji nie zależy od współpracy płyty i słupów rozpatrywanych jako elementy ramy oraz takiej w której przylegające przęsła nie różnią  się długościami więcej niż 25 %. W innych przypadkach należy przeprowadzić dokładne obliczenia zgodnie z normą [1], pkt. 6.4.3.

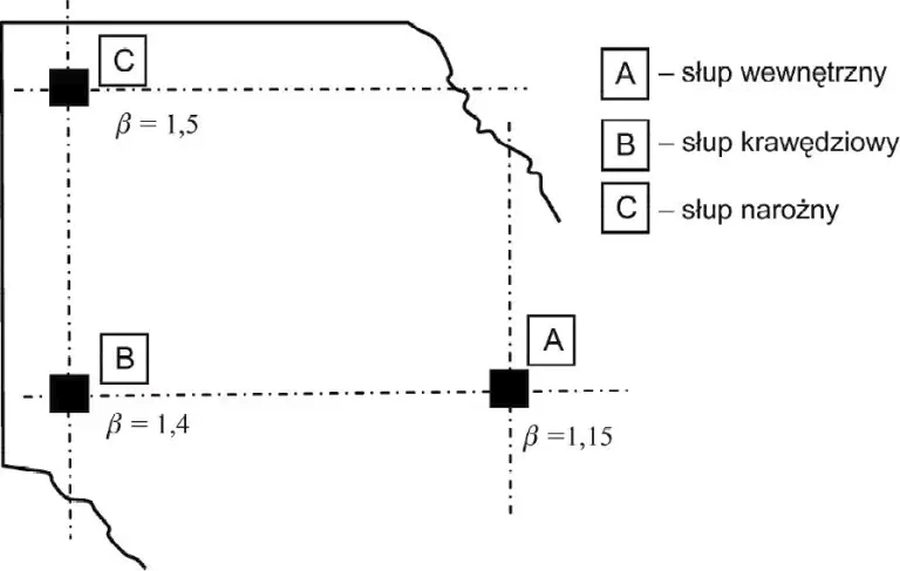
Rys. 3 Współczynnik położenia słupa  [1], rys. 6.21N

W załączniku krajowym do niemieckiego wydania Eurokod 2 [4] podano następujące przybliżone wartości współczynnika nierównomierności $\beta$  dla słupów w różnych lokalizacjach:
$$\begin{equation} \beta =\begin {cases}
1,1,& \textrm{wewnątrz płyty}\\
1,4,& \textrm{na krawędzi płyty}\\
1,5, & \textrm{w narożu płyty}\\
1,35,& \textrm{na krawędzi ściany}\\
1,20,& \textrm{w narożu ściany}\\
\end {cases} \label{5}\end{equation}$$

Współczynniki zwiększające $\beta$ rys.3 i $(\ref{5})$ stosuje isę również dla systemowych (patentowych)  rozwiązań zbrojenia na przebicie.

Redukcja obciążenia  ścinającego przez przebicie

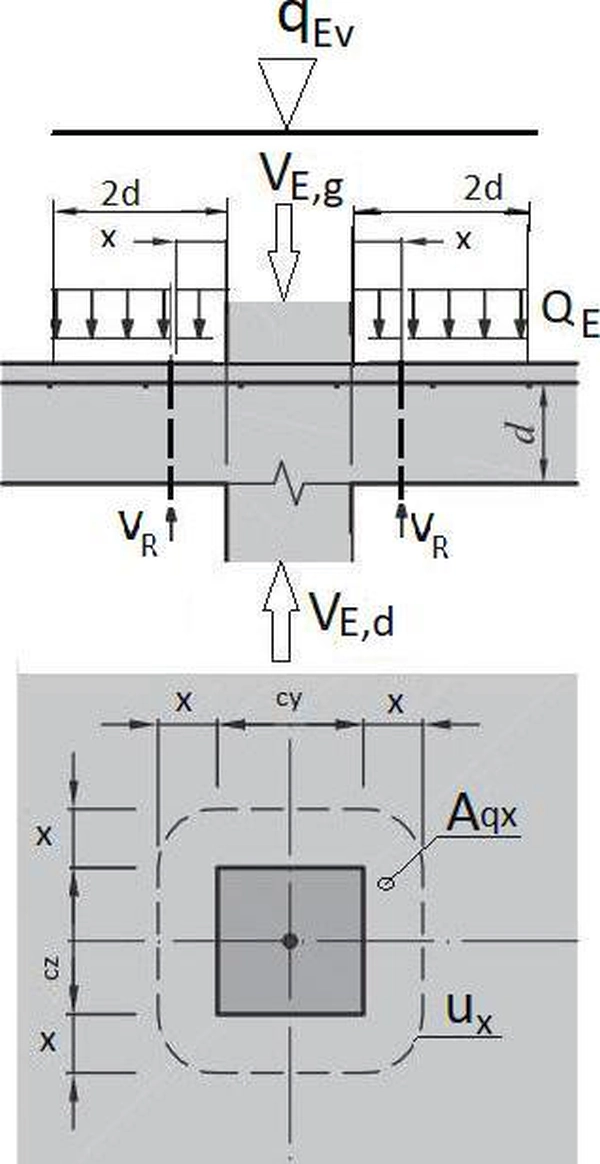
Zgodnie z zaleceniem normy [1], kl. 6.4.2(2), w przypadku, gdy sile skupionej przeciwstawia się duży, rozłożony równomiernie nacisk (np. odpór gruntu pod fundamentem), albo efekty reakcji lub obciążenia wewnątrz obszaru ograniczonego obwodem podstawowym $u_1$ (oddalonym o 2d od pola obciążenia ), to  należy wziąć pod uwagę obwód kontrolny $u_x$, leżący w odległości $x$  mniejszej niż 2d od tego pola (p. rys. 4)

Ponieważ  w praktyce płyty stropowe lub fundamentowe zawsze są obciążone powierzchniowo, obciążeniem $Q_E$ ( rys. 11), a cecha „duże obciążenie” nie jest jednoznaczna, więc zalecamy, by w każdym przypadku wyznaczyć położenie obwodu $u_out $ (poza którym zbrojenie na ścinanie przez przebicie nie będzie potrzebne.) z uwzględnieniem obciążeń powierzchniowych lub oporu gruntu.  Siła przebijająca strop nie jest w ogólnym przypadku siłą (reakcją) $V_E^g$ w słupie górnym (opartym na stropie) ani też siła $V_E^d$ w słupie dolnym (podpierającym strop).

W procedurze poszukiwania obwodu $u_{out}$ redukujemy siłę przebijającą płytę $V_{Ed}$, do wypadkowej sił pionowych $q_{Ev}$ działających na powierzchni obciążenia $A_{qx}$, nie większej niż powierzchnia $A_{q1}$ zamknięta obwodem podstawowym $u_1$) (rys. 8). Korzystne obciążenie rozłożone uwzględnia się więc wyłącznie w granicach obwodu podstawowego $u_1$, czyli dla $x \le 2d$. W zapisie symbolicznym formułę redukcji siły przebijającej można zapisać w postaci:

$$\begin{equation} V_{Ed, red}= \sum \limits _{A_{qx} \le A_{q1}}  q_{Ev}  \label{6}  \end{equation}$$

W sytuacji, pokazanej  na rys. 4 zredukowaną siłę przebijającą płytę stropową $V_{Ed, red}$  można wyznaczyć z zależności:

$$\begin{equation} V_{Ed,red}= \Delta V_{Ed} – A_{qx} \cdot  Q_{Ed} \label{7} \end{equation}$$

gdzie $\Delta V_{Ed}= V_{Ed,d} -V_{Ed,g}$  jest różnicą  sił w słupach pod (d)  i nad (g) płytą.

Rys. 4 Szkic do wyznaczania zredukowanej siły przebijającej strop

Pole obciążenia $A_{qx}$ wewnątrz rozpatrywanego obwodu kontrolnego $u_x$ wynosi:

$$\begin{equation} A_{qx} =\begin {cases}
2x(c_y+c_z)+\pi x^2+c_y c_z & \textrm{ w przypadku A}\\
2x(c_y+c_z)+\pi x^2 & \textrm{ w przypadku B}\\
\end {cases} \label{8}\end{equation}$$

gdzie:
przypadek A – pola bez słupa, np pole odporu gruntu pod fundamentem,
przypadek B – pola obejmujące słup, np. powierzchnia górna płyty na której stoi słup

Obwód kontrolny $u_x$ dla słupa wewnętrznego ma długość $(\ref {15})$ (lub $(\ref {17})$ , jeśli rozpatrujemy słup okrągły).

Warunek wytrzymałościowy na ścinanie przez przebicie

Warunkiem wytrzymałościowym ścinania przez przebicie jest warunek równowagi sił na obwodzie kontrolnym, który po uwzględnieniu zwiększenia siły  zewnętrznej  współczynnikiem nierównomierności $\beta$  oraz redukcji na skutek działania na płaszczyznę zawartą wewnątrz obwodu kontrolnego sił przeciwstawiających się przebiciu. podług formuły  ($\ref{7}$)   można zapisać krótko w postaci:

$$\begin{equation}  v_{Ed} \le v_{Rd}  \label{9} \end{equation}$$

gdzie:

$$\begin{equation}  v_{Ed}=\beta \cdot \cfrac{V_{Ed,red}} {u_x \cdot d} \label{10} \end{equation}$$

są obliczeniowym  naprężeniem stycznym od obciążeń zewnętrznych w przekroju kontrolnym $A_x= u_x \cdot d$ , gdzie:
($d=h-c-\Phi/2$) –  wysokość efektywna przekroju ; $h$ – wysokość  płyty, $c= c_{nom}$ – otulenie  podłużnego zbrojenia  rozciąganego o średnicy $\Phi$,
$u_x$ – obwód przekroju kontrolnego, przyjmowany zależnie od  miejsca w którym sprawdza się warunek wytrzymałościowy ($\ref{9}$),

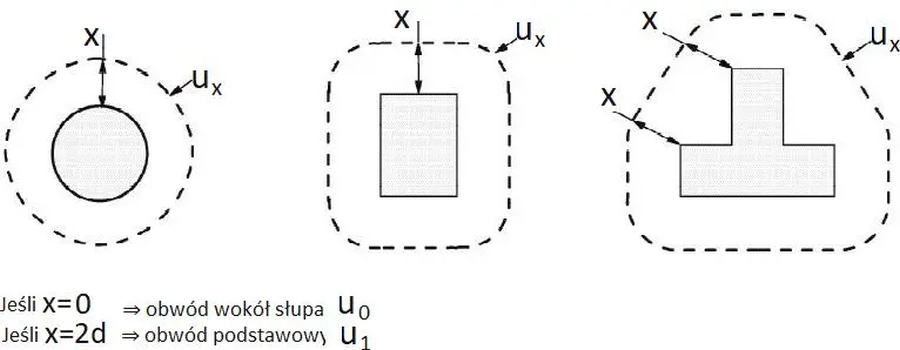
Prkatycznie ważne sa trzy obwody kontrolne:
$u_0$ – obwód w licu słupa,
$u_1$ – obwód podstawowy w odległości $2d$ od lica słupa,
$u_{out}$ – obwód skrajny – nadalszy pbwód  kontrolny, w którym nie jest już wymagane zbrojenie płyty na ścinanie przez przebicie.
Sposób wyznaczania obwodu przekroju kontrolnego omówiono szczegółowo w rozdziałach  obwód i przekrój kontrolny oraz skrajny obwód kontrolny.

W projektowaniu wstępnym często pomija się redukcję zewnętrznej siły przebijającej strop przez odciążające obciążenie rozłożone działające wewnątrz powierzchni objętej obwodem kontrolnym,  czyli przyjmuje sie patrz  rys. 4

$$\begin{equation}  V_{E,red}= V_{E,d}^d – V_{E.d}^g \label{11} \end{equation}$$

Obliczeniową nośność na ścinanie przez przebicie $v_{Rd }$ wyznacza się z ogólnych  zależności normy [1] dla ścinania przekroju żelbetowego  i syntetycznie omówionych  w artykule Ścinanie i skręcanie belek żelbetowych  [ŚSBŻ] w zależności od  możliwego  mechanizmu zniszczenia płyty przez ścinanie na przebicie w danym przekroju kontrolnym.

Występują trzy kombinacje obwodu kontrolnego oraz właściwej dla niego nośności przkroju betonowego ( naprężeń dopuszczalnych)
[obwód  ;  nośność)] =  [ $U_x \,;\,  \,v_{Rd,x}$]:

[U₀ ,v_Rd,max ]  [ $u_0$ – obwód kontrolny wokół słupa ; $v_{Rd,max}$ – wytrzymałość ściskanego krzyżulca betonowego]
Na obwodzie $u_0$   może wystąpić mechanizm przekroczenia nośności krzyżulców betonowych.
Nośność $v_{Rd,max}$  w zagadnieniu ścinania przez przebicie przyjmuje się  z  formuły (19)  {ŚSBŻ]: , która można zapiać w postaci

$$\begin{equation}  v_{Rd,max} = 0, 24 \cdot f_{cd} \cdot ( 1- f_{ck}/ 250) \label{12} \end{equation}$$

Jeśli nie jest spełniony warunek  U0,  to należy skorygować obwód słupa, grubość płyty lub wykonać słup z głowicą,
Bez  doprowadzenie do spełnienia  warunku U0  (dla krzyżulca betonowego $ v_{Rd,max}$)  nie można przejść do kolejnego kroku.

[U₁ ,v_Rd,c ]  [ $u_1$  – podstawowy obwód kontroly ; $v_{Rd,max}$ – wytrzymałość betonu bez zbrojenia na ścinanie]
Na obwodzie podstawowym $u_1$, czyli w odległości $x=2d$ od lica słupa  może wystąpić mechanizm przekroczenia nośności betonu bez zbrojenia na ścinanie  (ale zbrojonego poodłużnie na zginanie).
Nośność $v_{Rd,c}$  wyznacza się  z fomuły  (13) {ŚSBŻ]

Jeśłi nie jest spełniony warunek U1 ( wytrzymałosći betonu nie zbrojonego) to należy zaprojektować zbrojenie na przebicie w sposób opisany w rozdziale  zbrojenie na ścinanie przez przebicie. Zbrojenie  na ścinanie przez przebicie wymagane jest aż do przekroju skrajnego $u_{out}$.

[U_out ,v_Rd,cs ]  [ $u_{out}$ – skrajny obwód kontrolny ; $v_{Rd,cs}$ – wytrzymałości betonu ze zbrojeniem na ścinanie]
Na obwodzie $u_{out} $, czyli w odległości $x_{out}$ od lica słupa  jest już spełniony warunek wytrzymałosćiowy dla wytrzymałości betonu bez zbrojenia na ścinanie $v_{Rd,c}$, a przed tym przekrojem zbrojenie na ścinanie o nośności  ($\ref{32}$) lub ($\ref{33}$)jest jeszcze potrzebne.

Obwód i przekrój kontrolny

Obwody kontrolne wokół słupa

Definiuje się obwody kontrolne  wokół słupa i przekroje kontrolne wyznaczone przez obwód i przebiegające na wskroś płyty, na których może zajść ścięcie płyty poprzez przebicie. W ogólności przekrój kontrolny może przebiegać w odległości $x$ od krawędzi słupa, co dla kilku  kształtów przekroju słupa, pokazano na rys, 4. 

Rys. 5. Kształty obwodu kontrolnego wokół słupa wewnętrznego

W normie [1] definiuje się przekrój wokół słupa $u_0$, przekrój podstawowy $u_1$, przebiegający w odległości  $2d$ od lica słupa oraz przekrój $u_{out}$ , to jest najdalszy przekrój kontrolny, w którym nie jest już wymagane zbrojenie płyty na ścinanie przez przebicie.

Obwody kontrolne umieszczone poza krawędziami słupa $u_x$ (oprócz $u_0$) mają ten sam kształt, ale różnią się długością.

Wymiar $d$ jest wysokością użyteczną płyty, a  nie jej całkowitą grubością . Zgodnie z definicją wprowadzoną w konstrukcjach żelbetowych , $d$  jest odległością od osi podłużnego  zbrojenia rozciąganego do powierzchni płyty (p. rys.8).

Przekrojem kontrolnym $A_x$ jest przekrój o wysokości użytecznej $d$, rozciągający się wzdłuż obwodu kontrolnego $u_x$.

W płytach o stałej grubości przekrój kontrolny jest prostopadły do środkowej powierzchni płyty. Wówczas $A_x=u_x\cdot d$.  Dla  płyty o różnych wysokościach użytecznych $d_y$ oraz $d_z$ w dwóch ortogonalnych kierunkach, wysokość użyteczną przyjmuje się jako średnią arytmetyczną  $d=({d_y+d_z})/2$.

Obwody kontrolne  słupa wewnętrznego, brzegowego i narożnego

Obwód $u_0$ wokół słupa prostokątnego

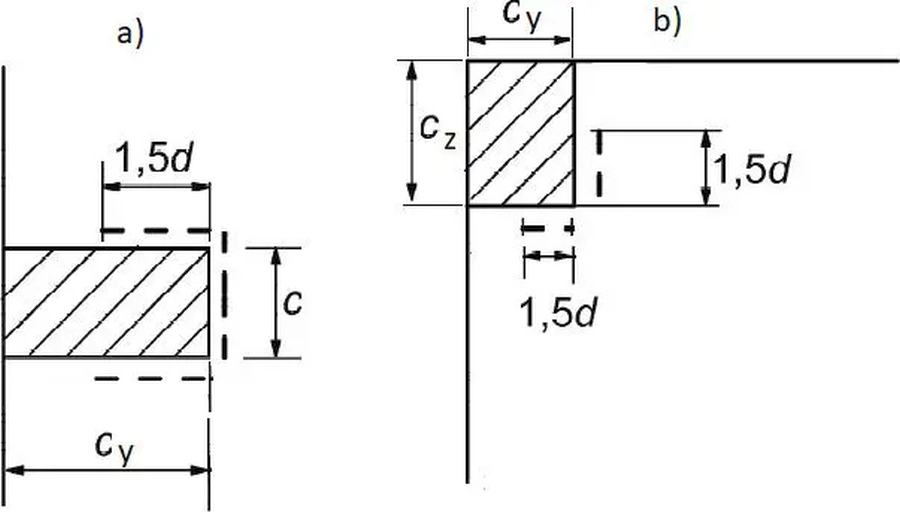
Obwód kontrolny $u_0$ wokół słupa  prostokątnego o bokach: poziomym $c_y$ i pionowym $c_z$ (rys.5),  przyjmuje się zgodnie z regułą [1], pkt . 6.4.5 (3) (p. również rys. 6):

$$\begin{equation} u_0 =\begin {cases}
2 (c_y+c_z), & \textrm{dla słupa wewnętrznego}\\
c_z+3d \le (c_z+2c_y), & \textrm{dla słupa brzegowego}\\
3d \le (c_y+c_z), & \textrm{dla słupa narożnego}\\
\end {cases} \label{13}\end{equation}$$

Rys.6 Obwód kontrolny u₀ dla prostokątnego słupa: a) obrzeżnego, b) narożnego

Obwód $u_0$ wokół słupa okrągłego

W przypadku słupa okrągłego o średnicy $\Phi$  przyjmuje się przez analogię oszacowania:

$$\begin{equation} u_0 =\begin {cases}
\pi  \Phi  & \textrm {dla słupa wewnętrznego}\\
3d \le 3/4 \cdot \pi  \Phi & \textrm{dla słupa brzegowego}\\
3d \le 1/2 \cdot \pi  \Phi  & \textrm {dla słupa narożnego}\\
\end {cases} \label{14}\end{equation}$$

choć nie zaleca się lokalizowania krawędzi słupa okrągłego w odległości  $K\le 2d$ od krawędzi płyty.

Obwód $u_x$ w tym podstawowy $u_1$ wokół słupa prostokątnego

W przypadku położenia słupa blisko krawędzi płyty obwód $u_x$ nie może przekraczać długości linii przerywanych, naniesionych na rys. 7

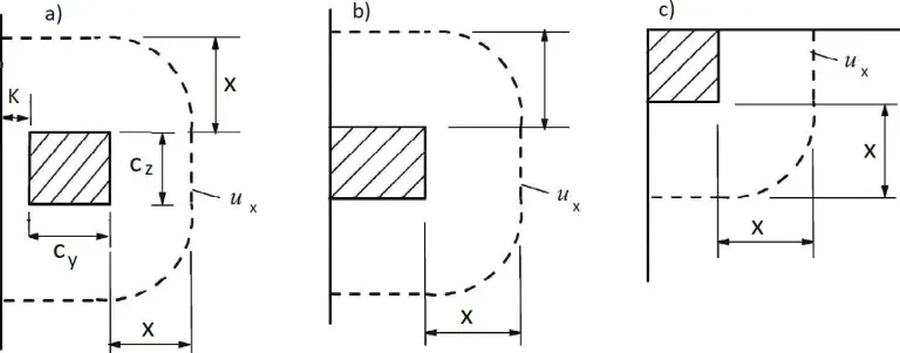
Rys.7 Obwód u_x dla słupa położonego blisko krawędzi: a),b) brzegowy, c) narożny (zmodyfikowane [1], rys. 6.15

W przypadku słupa prostokątnego z krawędzią oddaloną o K brzegu płyty ( lub dla słupa narożnego o $K_y$, $K_z$ od odpowiednich brzegów płyty) – reguły  zaprezentowane  na rys. 6 i rys. 7, prowadzą to do formuły:

$$\begin{equation} u_x =\begin {cases}
u_{xP} & \textrm{dla słupa wewnętrznego}\\
2(K+c_y+c_z)+ \pi x \le u_{xP} & \textrm{dla słupa brzegowego}\\
K_y+K_z +c_y+ c_z + \pi x/2 \le u_{xP} & \textrm{dla słupa narożnego}\\
\end {cases} \label{15}\end{equation}$$

gdzie:
$$\begin{equation} u_{xP} =2(c_y+c_z + \pi x) \label {16} \end{equation}$$

Obwód $u_x$ w tym podstawowy $u_1$ wokół słupa okrągłego

W przypadku słupa okrągłego  z krawędzią oddaloną o $K_x$ i $K_y$ od brzegów płyty otrzymujemy formuły:

$$\begin{equation} u_x =\begin {cases}
u_{xF} & \textrm{dla słupa wewnętrznego}\\
u_{xF} – L_K & \textrm{dla słupa brzegowego}\\
u_{xF} –  L_{Kx}-L_{Ky} & \textrm{dla słupa narożnego}\\
\end {cases} \label{17}\end{equation}$$

gdzie:
$$\begin{equation} u_{xF} =2 \pi R_x \label {18} \end{equation}$$

$R_x=(\Phi/2+x)$ – promień  obwodu kontrolnego,
$ L_K =2R_x \cdot (\pi- arccos(1 – \tfrac{K}{R_x})$ – długość obwodu kontrolnego, pozostająca poza  brzegiem płyty, oddalonym o K od krawędzi słupa.

Zredukowane obwody słupa blisko otworów w płycie

Jeżeli pole obciążenia leży blisko otworów i najmniejsza odległość od krawędzi słupa do otworu nie przekracza 6d, to część obwodu kontrolnego, zawartą między dwiema ukośnymi liniami biegnącymi od środka pola obciążenia do zewnętrznej krawędzi otworu, wyłącza  się ją z obwodu kontrolnego, zgodnie rys 8.

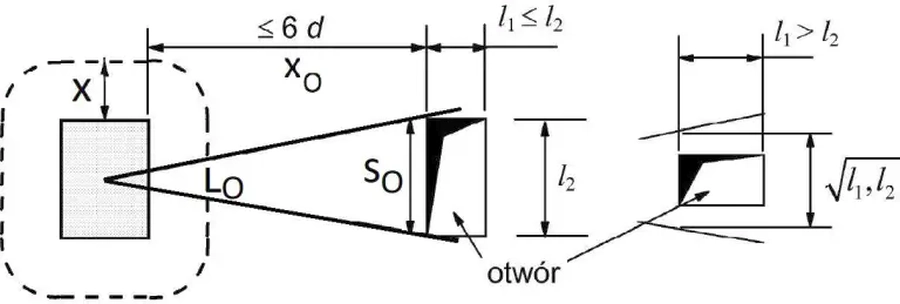
Rys. 8  Obwód kontrolny zredukowany w pobliżu otworów w płycie [1], rys. 6.14

Długość wycięcia w obwodzie $L_O$ zwykle określa się rysunkowo. Dla prostego przypadku pokazanego na rys. 8 można podać formułę:

$$\begin{equation} L_O= s_O \dfrac {c_y+x} {c_y+x_O} \label {19} \end{equation}$$

gdzie:

$s_O= l_2 \text{ (jeśli $l_2$ > $l_1$) } \text {  lub } =\sqrt{ l_1 \cdot l_2} \text{ (  jeśli $l_2$ < $l_1$) }$ – szerokość zastępcza otworu

$x_O$ – odległość krawędzi otworu od lica słupa.

Model przebicia wybranych elementów konstrukcyjnych

Ścinanie przez przebicie płaskiej płyty stropowej

Doświadczenia wskazują, że siła niszcząca rozchodzi się pod katem $\Theta=arctan (1/2)$ w sposób pokazany na rys. 9 (p. również fotografia – rys.1) Zniszczenie płyty przy przebiciu polega na wyrwaniu fragmentu płyty wokół słupa na obwodzie podstawowym $u_1$ poprzez ścięcie przekroju $A_1$.

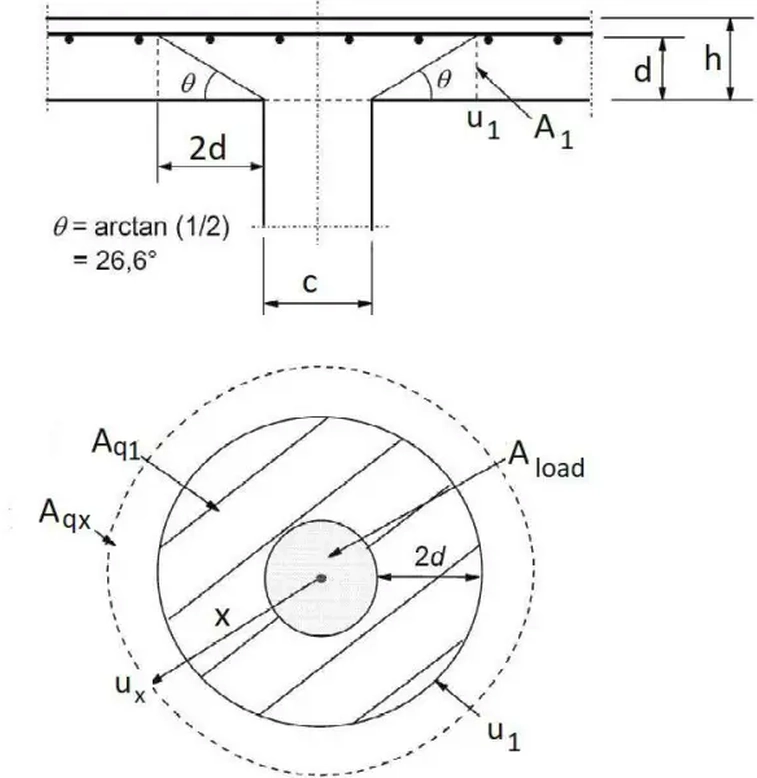
Rys.9 Model przebicia [1]

Równomiernie rozłożone  obciążenie obliczeniowe $Q_{E}$ na  płycie stropowej (rys. 4) jest skutkiem działania ciężaru własnego płyty konstrukcyjnej wraz z warstwami wykończeniowymi i ewentualnie  stropu podwieszonego $G_k$ obciążenia użytkowe na stropie $Q_{k,u}$ , zastępczego obciążenia od ścianek działowych i urządzeń $Q_{k,ś}$, instalacji i urządzeń podwieszonych pod stropem $Q_{k,p}$. Wyznacza się je jako obciążenie kombinacyjne zgodnie z zasadami omówionymi w artykule Kombinacje obciązeń w Eurokodach,.  Najczęściej  stosowaną regułą kombinacyjną jest:

$$\begin{equation} Q_E = Q_{E.d} = 1,35 \cdot G_k+1,5 \cdot ( 1 \cdot Q_{ku}+0,7 \cdot Q_{k,ś} +0,7 \cdot Q_{k,p} \label{20} \end{equation}$$

Z warunku wytrzymałościowego $(\ref{9})$ po rozwiązaniu stosownego równania ze względu na $x$, otrzymamy wwyrażenie na odległość obwodu od lica słupa $x_{max}$:

$$\begin{equation}  x_{max}= \left ( \sqrt{ [ \pi \Delta V_{Ed}/Q_{Ed}+ (c_y+c_z)^2  +d_{v/Q}^2] } – (c_y+c_z) \right ) / \pi – d_{v/Q}  \label {21} \end{equation}$$

gdzie:
$d_{v/Q}= [v_{Rd}/(\beta Q_{Ed})]\cdot d$

Równanie $(\ref{21} )$ uzyskano bez ograniczenia pola obciążenia do pola zamkniętego obwodem podstawowym. jako pierwiastek równania kwadratowego  Po wprowadzeniu ograniczeń zespół równań i nierówności staje się strukturalnie nieliniowy i właściwym sposobem rozwiązania staje się zastosowanie procedur numerycznych.  W przykładach do niniejszego artykułu zaprezentowano wyznaczanie położenia obwodu krytycznego z zastosowaniem arkusza kalkulacyjnego „Przebicie.xls”,

Ścinanie przez przebicie  fundamentu i stropu ze  słupem z głowicą

Płyty na słpach z głowicami

W płytach i fundamentach o zmiennej grubości, innych niż fundamenty schodkowe; za wysokość użyteczną można przyjąć wysokość na obwodzie pola obciążenia w sposób pokazany na rys. 10 na przykładzie stopy słupa.

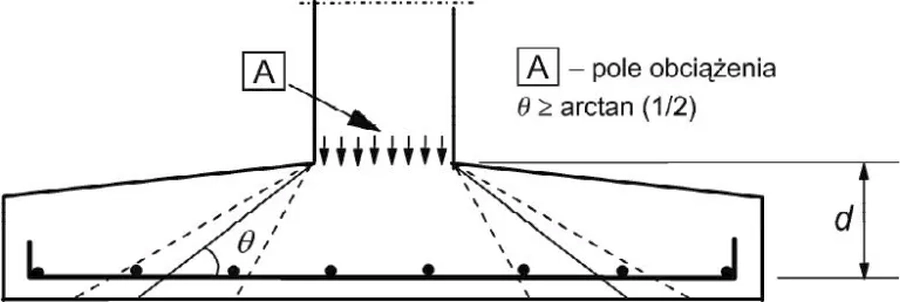
Rys. 10 Ukośny przekrój kontrolny na przykładzie stopy słupa [1], rys. 6.16

Głowica („grzybek”) słupa  generuje przekrój kontrolny , pokazany na rys. 11. Przy sprawdzaniu głowicy słupa, w miejsce $d$ należy podstawiać $d_H$ (rys. 11b). 

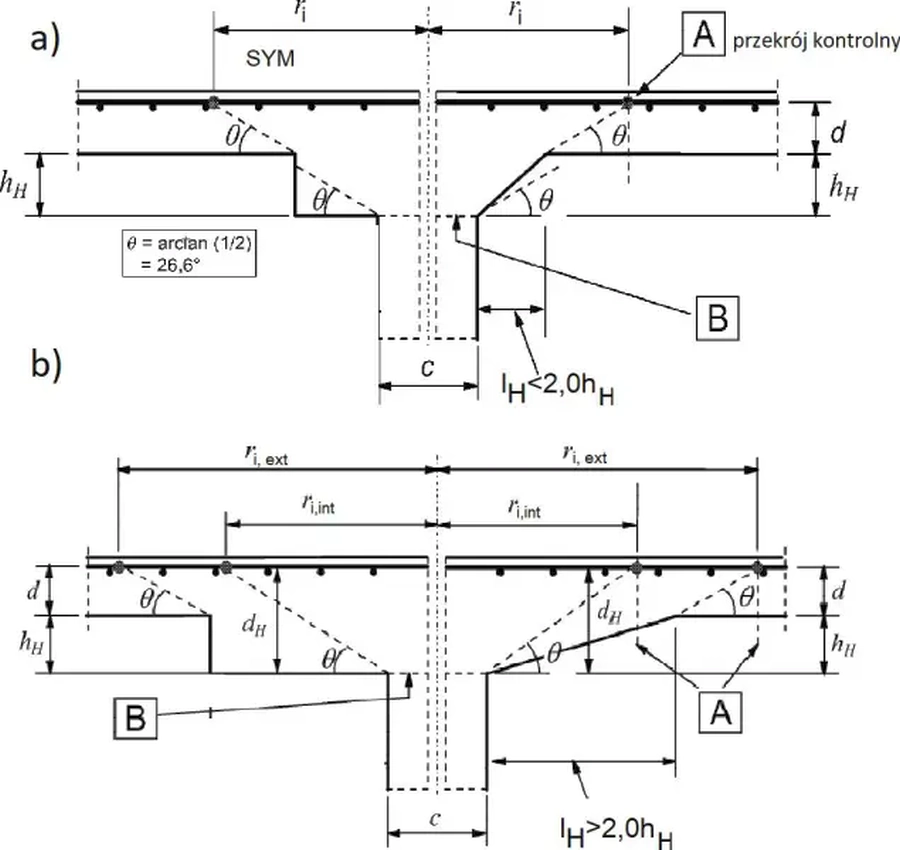
Rys. 11. Przekrój kontrolny w głowicy słupa: a) dla l_H<2h_H, b) dla l_H>2h_{H [1], rys. 6.17-6.18}

W płytach opartych na okrągłych głowicach słupów o średnicy Ø, dla których l_H<2h_H (rys.11a) , gdzie $l_H$ jest odległością od krawędzi słupa do krawędzi jego głowicy, sprawdzenie naprężeń stycznych przy przebiciu jest potrzebne tylko w przekroju kontrolnym, lezącym na zewnątrz czoła słupa. Odległość tego przekroju od środka słupa $r_i$ można obliczyć ze  wzoru

$$\begin{equation} r_i=2\cdot d+l_H+Ø \qquad r_{i,int}=2\cdot (d+h_H)+ Ø/2 \qquad r_{i,ext}=2\cdot d+l_H+ Ø/2 \label {22} \end{equation}$$

Natomiast dla słupa prostokątnego z prostokątną głowicą dla $l_H <2h_H$ o wymiarach głowicy $l_1\, \times \, l_2$ przy zachowanym warunku: $l_1=(c_1+2\cdot l_{H1}) \, < \, l_2=(c_2+2\cdot l_{H2})$ wyznacza sie z zależności:
$$\begin{equation} r_i=2 \cdot d\cdot min[0,56\sqrt{l_1\cdot l_2} \, ; \, 0,69 \cdot l_1] \label {23} \end{equation}$$

Jeżeli $ l_H > 2\cdot h_H$ (rys. 11b), to w płytach z głowicami należy sprawdzać przekroje kontrolne leżące zarówno w głowicach, jak i w płycie.

Fundamenty

Odpór fundamentu należy wyznaczać zgodnie z normą [5] z rozwiązania zadania odkształcalnej płyty, ławy lub stopy, spoczywającej na jednostronnym podłożu Winklera (nie przenoszącym odrywania).  Na rys. 12 pokazano rozkład odporu gruntu, traktowanego jako dwustronne  lub jednostronne podłoże Winklera o współczynniku sprężystości C pod kwadratową stopą fundamentową AxB.

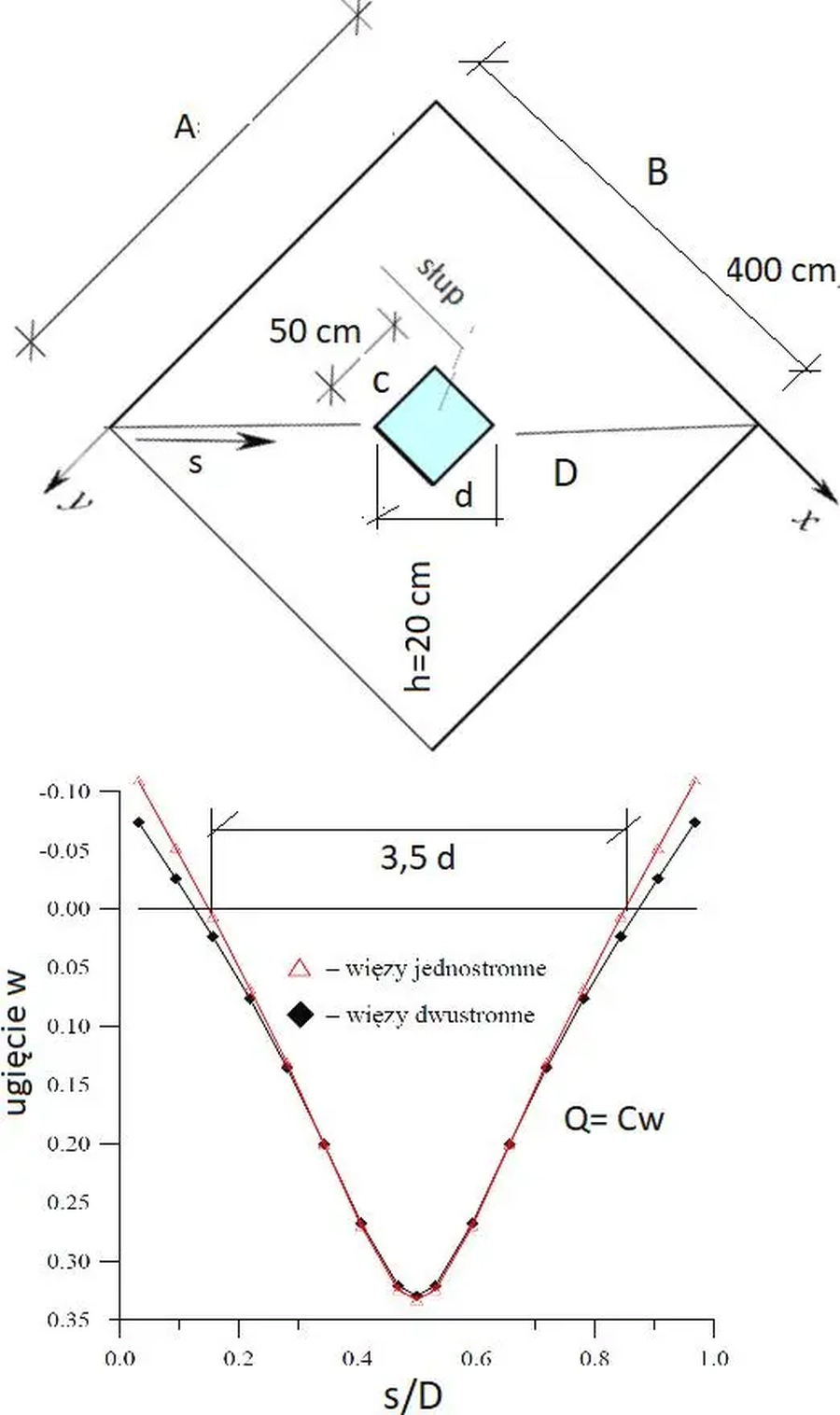
Rys.12 Rozkład odporu gruntu Q pod odkształcalną stopą fundamentową – zmodyfikowane [6]

Odpór gruntu jest największy tuż pod słupem, a krawędzie stopy są odrywane od podłoża. W każdym indywidualnym przypadku  rozkład odporu pod fundamentem będzie ilościowo różny  i zależny od sztywności fundamentu oraz rodzaju podłoża gruntowego, ale charakter rozkładu jest podobny.

Przyjmiemy, że siła przebijająca $V_{Ed}$ wywołuje  pod fundamentem o wysokości $h_f$ naprężenia $Q_{E,f}$, które rozkładają się na powierzchni $A_{Q,f}$ mniejszej od podstawy fundamentu $A_f= A \cdot B$. Powierzchnia $A_{Q,f}$ rozciąga się po $2,5 h_f$ w każdą stronę of lica słupa.
Na przykład w sytuacji pokazanej na rys. 12 mielibyśmy $A_{Q,f}=(0,40 + 2 \cdot 2,5 \cdot  0,2 )^2 =1,96 \, m^2$,  co jest zgodne  z przykładem na rysunku ( $A_{Q,f}= (3,5c)^2 = (3,5 \cdot 0,4)^2 = 1,96 \, m^2$).

Przy założeniu jak wyżej, otrzymujemy następującą formułę do oszacowania odporu gruntu w obszarze słupa pod fundamentem

$$\begin{equation} Q_{Ed,f} = \dfrac{V_{E,d} }{A_{Q,f}} \label{24} \end{equation}$$

gdzie

$$\begin{equation}A_{Q,f}=a_f \cdot b_f \qquad  a_f=(c_y+5h_f) \qquad b_f=(c_z +5h_f) \label{25} \end{equation}$$

W przypadku płyty (lub stopy) fundamentowej  zredukowana siła przebijająca wynosi więc

$$\begin{equation} V_{Ed, red,f}= V_{Ed, g} -A_{qx} \cdot  Q_{E,d,f}= V_{Ed, g} \left (1- \tfrac {A_{qx}} {A_{Q,f}} \right ) \label{26} \end{equation}$$

Pod fundamentem nie ma słupa , więc kontrolne pole $A_{qx}$ szacuje się z formuły $(\ref{8})$ dla przypadku A.

W przykładach do niniejszego artykułu zaprezentowano wyznaczanie położenia obwodu krytycznego z zastosowaniem arkusza kalkulacyjnego „Przebicie.xls”, w którym przyjęto formułę $(\ref{25})$ do szacowania równomiernie rozłożonego odporu gruntu w obszarze słupa pod fundamentem. Tekst źródłowy arkusza jest załącznikiem do przykładów.

Zbrojenie na ścinanie przez przebicie

Zasady ogólne

Generalnie do doboru elementu żelbetowego ze względu na nośność  na ścinanie stosuje się  trzy podejścia:

P1 podejście, w którym dobiera się wymiary betonu, tak by zbrojenie na ścinanie nie było wymagane. Podejście jest stosowane w zwykłych płytach, bo najczęściej po doborze elementu na pierwszorzędne warunki (najczęściej zginanie, i ugięcia)- nie wymaga on  zbrojenia na ścinanie,

P2 podejście, w którym z góry zakłada się potrzebę zbrojenia na ścinanie. Podejście jest stosowane w belkach i prętach, w których zbrojenie na ścinanie dobiera się w celu przeniesienia naprężeń stycznych wywołanych siłami poprzecznymi. Do tego celu najczęściej stosuje się strzemiona, które przejmują poziome siły ścinające (siły rozwarstwiające, są  równe pionowym siłom ścinającym,co wynika z elementarnych warunków równowagi przekroju). Rzadziej stosuje się pręty ukośne nachylone pod takim kątem jak naprężenia główne w przekroju zginanym i ścinanym , czyli pod katem ok $45^o$.

P3 podejście , w którym zbrojenie na ścinanie jest zastosowane dopiero wówczas, gdy wykaże się, że przekrój nie zbrojony ma niewystarczającą nośność. Własnie takie podejście stosuje się w rozważanym przypadku zbrojenia płyt na przebicie.
W celu zaprojektowania zbrojenia na ścinanie przez przebicie poszukuje się obwodu kontrolnego poza którym zbrojenie na ścinanie nie jest już wymagane. Taki obwód jest nazywamy skrajnym obwodem kontrolnym $u_{out}$  $(\ref{27})$.

Skrajny obwód kontrolny u_out

Z podstawowego warunku  wytrzymałościowergo ($\ref{9}$)  po przekształceniu uzyskamy długość skrajnego obwodu kontrolnego $u_{out}$ poza którym zbrojenie na ścinanie nie jest  juź wymagane [1],(6.54):

$$\begin{equation} u_{out}= \beta \cdot \dfrac {V_{Ed}}{v_{Rd,c} \cdot d} \label{27} \end{equation}$$

Przekrój zbrojenia na ścinanie

Wewnątrz skrajnego obwodu potrzebne jest  zbrojenie na ścinanie.

Pole przekroju zbrojenia obwodu ścinanego $A_{sw}$ w $mm^2$ wyznaczamy z warunku wytrzymałosciowego $(\ref{9})$ na zazbrojonym obwodzie podstawowym, czyli  dla:
$(\ref{10})$ $\to$ $v_{Ed} = v_{Ed,1}= v_{Ed}(x=2d)$
$v_{Rd}=v_{Rd,cs}$  $(\ref{32})$,  skąd dla klasycznego zbrojenia strzemionami:

$$\begin{equation} A_{sw} \ge \dfrac{ v_{Ed,1} – 0,75 \cdot v_{Rd,c}} {1,5 \cdot f_{ywd,ef} \cdot sin \alpha } \cdot s_r \cdot u_1 \label{28} \end{equation}$$

Przyjmuje się, że zbrojenie na  ścinanie ma efektywną wytrzymałość  obliczeniową

$$\begin{equation} f_{y,fd,ef}= min[ 250+0,25d \, ; \, f_{ywd}] \label{29} \end{equation}$$

Średnią wysokość użyteczną przekroju $d$ podstawia się w mm, a wynik uzyskuje w MPa.

$f_{ywd}$ jest obliczeniową granicą plastyczności stali zbrojeniowej na ścinanie , którą wyznacza się w zależności od sposobu wytężenia danego pręta (lub grupy) prętów przenoszących ścinanie. Najczęściej zbrojenie na ścinanie umieszcza się tak, by pręty przenosiły siły osiowe wywołane ścinaniem przekroju (same pręty nie są ścinane) i $f_{ydw}=f_{yd}$, gdzie wytrzymałość obliczeniowa stali na rozciąganie wyznacza się ze standardowej zależności $f_{yd}=f_{yk} / \gamma_s$, gdzie $f_{yk}$ – charakterystyczna granica plastyczności stali zgodna z wyróżnikiem klasy stali, np dla powszechnie stosowanej stali B500 $f_{yk}=500$ MPa, a współczynnik materiałowy dla stali zbrojeniowej w Polsce przyjmuje się o wartości $\gamma_s$=1,15, czyli dla stali B500

$f_{ywd}=f_{yd}=500/1,15=434,8$ MPa.

We wzorze ($\ref{28}$):

$ s_r$ jest promieniowym rozstawem obwodów zbrojenia na ścinanie,

$\alpha$ -kąt między zbrojeniem na ścinanie  a płaszczyzną płyty. Dla najczęściej stosowanych strzemion prostopadłych do powierzchni płyty $ sin \alpha$ =1.

Jeżeli zbrojenie na ścinanie składa się z prętów odgiętych rozmieszczonych wzdłuż jednej tylko linii, to stosunkowi $d/s_r$ w wyrażeniu ($\ref{28}$) można nadać wartość 0,67.

Skrajny obwód zbrojenia

Na rys. 13 pokazano dwa główne sposoby zbrojenia na ścinanie przez przebicie: obwodowo-promieniowe [A} i ortogonalne. [B]

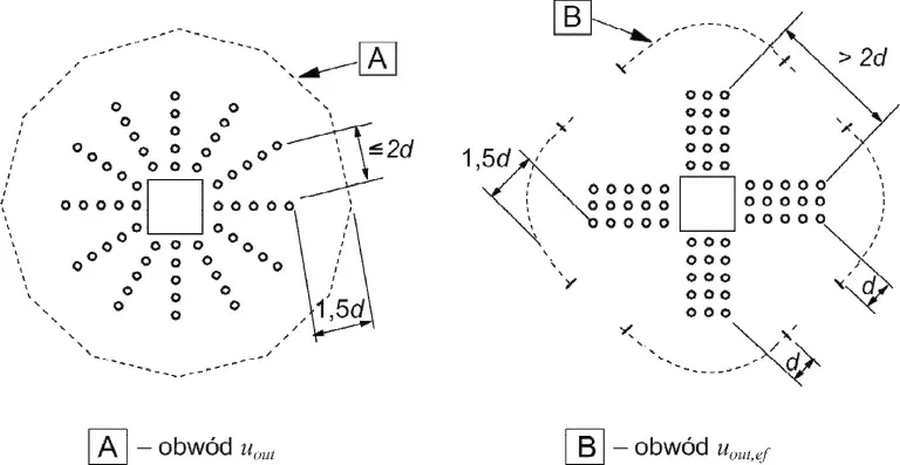
Rys. 13 Skrajny obwód zbrojenia [1],rys. 6.22

Promień $r_{out}$ skrajnego obwodu  kontrolnego $u_{out}$ przy zbrojeniu promieniowym (rys. 13a ), lub $u_{out,eff}$  przy zbrojeniu ortogonalnym ( rys. 13b)  wyniesie

$ r_{out}= \cfrac{u_{out}} {2\pi}$  (licząc od środka słupa) .

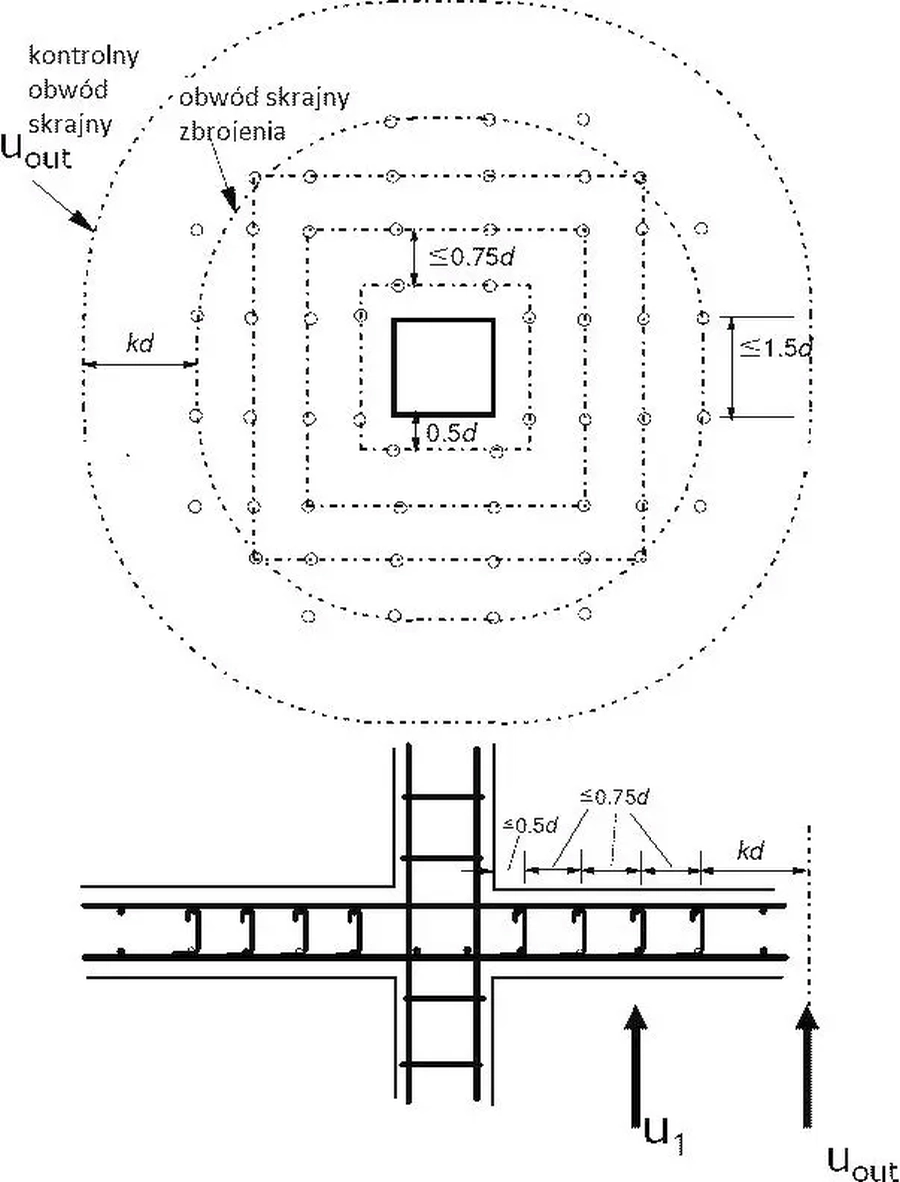
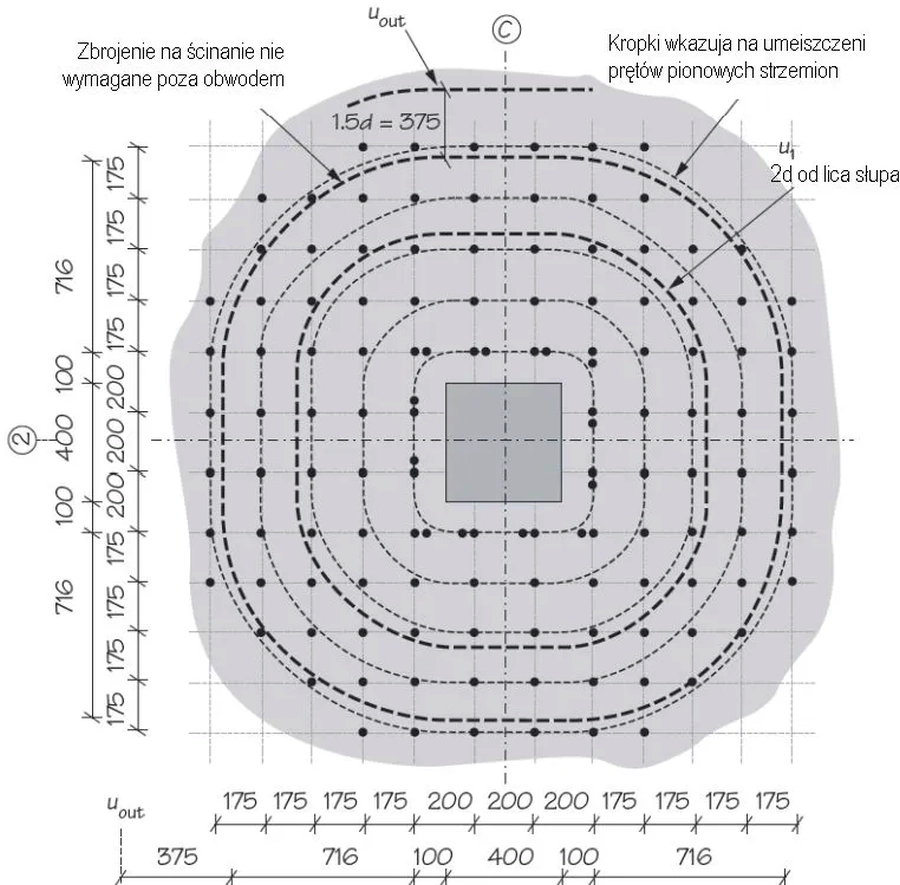
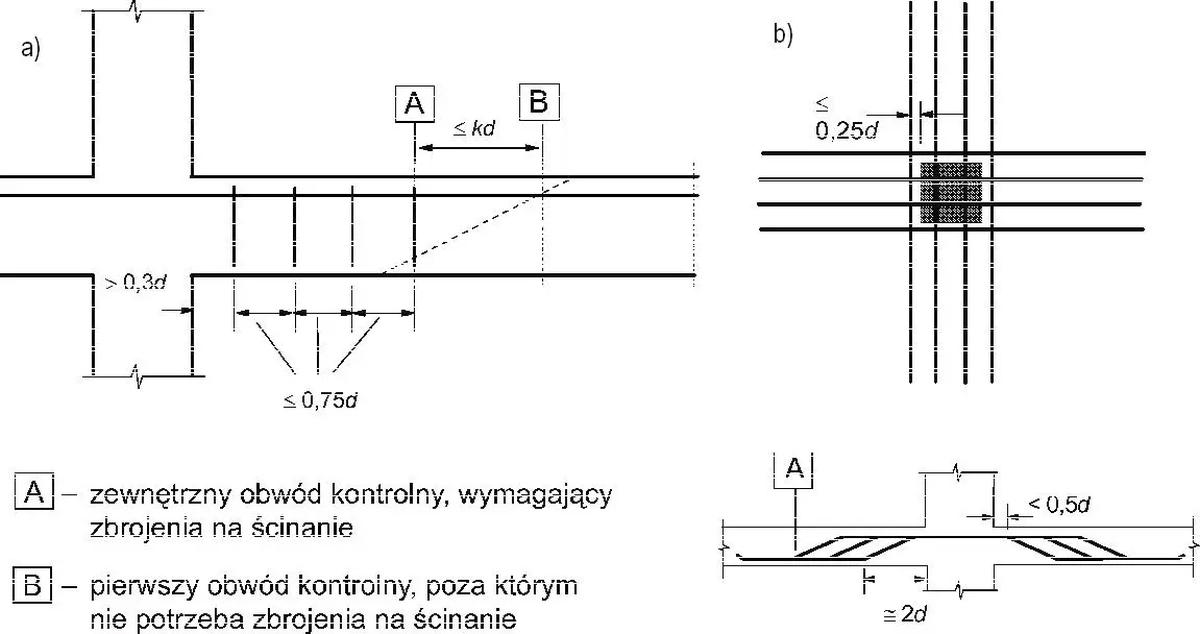
Od skrajnego obwodu kontrolnego należy odróżnić skrajny obwód zbrojenia, który należy umieścić w głębi obszaru kontrolnego w odległości nie większej niż $k\cdot d$, gdzie $k=1,5$ .  Na rys. 14 pokazano wzajemne usytuowanie skrajnego obwodu kontrolnego $u_out$  oraz skrajnego obwodu zbrojenia, a także układ zbrojenia na ścinanie strzemionami. Na tym rysunku zaprezentowano  zalecenia, opisane  w kolejnym punkcie artykułu.

Rys.14 Skrajne obwody: kontrolny u_out i zbrojenia oraz układ zbrojenia strzemionami

Konstruowanie zbrojenia na ścinanie przez przebicie

Zbrojenie na ścinanie przez przebicie konstruuje się z użyciem strzemion lub prętów odgiętych podobnie jak w belkach. W praktyce najczęściej stosuje się zbrojenie strzemionami  (przy mniejszych siłach poprzeczych) lub za pomocą bolców HALFEN, JORDAHL PSB, EBEA lub innych. ze względu na ich znacznie lepszą efektyność od klasycznego zbrojenia na ścinanie.poprzeczne   

Rys.15 Zbrojenie na ścinanie przez  przebicie: a) strzemionami, b) prętami odgiętymi [1],rys. 9.10

Zbrojenie na ścinanie przzez przebicie rozmieszcza się pomiędzy obciążoną powierzchnią (słupem) i obwodem leżącym wewnątrz obwodu kontrolnego, poza którym zbrojenie na ścinanie nie jest już wymagane, nie dalej niż $k\cdot d$ od tego obwodu, co pokazano na rys. 15, przy czym należy zastosować co najmniej dwa obwody złożone z ramion strzemion (rys.15a), a rozstaw obwodów złożonych z ramion strzemion nie powinien przekraczać $3/4 d$.

Ponadto rozstaw ramion strzemion wzdłuż obwodu nie powinien przekraczać 1,5d wewnątrz pierwszego obwodu kontrolnego (oddalonego 2d od obciążonej powierzchni) oraz nie powinien przekraczać 2d w tych częściach obwodów; lezących na zewnątrz pierwszego obwodu kontrolnego, które wpływają na nośność na ścinanie (rys.15a).
W przypadku prętów odgiętych rozmieszczonych jak na rys 15b jeden obwód ramion strzemion można uznać za wystarczający.

Pole przekroju jednego ramienia strzemiona (lub równoważne pole zbrojenia innego rodzaju)$A_{s1,min}$ powinno spełniać warunek

$$\begin{equation} A_{s1,min}\cdot \dfrac {1,5sin\alpha + cos\alpha}{s_r\cdot s_t} \ge 0,08 \dfrac{\sqrt{f_{ck}}}{f_{yk}} \label {30} \end{equation}$$

gdzie:

$s_r , \, s_t $ – rozstaw strzemion odpowiednio w kierunku promieniowym (odległości między okręgami) i stycznym (na okręgu),

$\alpha$ – kąt między zbrojeniem na ścinanie i zbrojeniem głównym (tj. dla strzemion pionowych \alpha= 90°, (sin \alpha+cos \alpha)=1.

Na zbrojenie  przy przebiciu można stosować pręty odgięte; które przechodzą przez powierzchnię obciążoną albo leżą w odległości nie przekraczającej d/4 od tej powierzchni  (rys. 15b u góry).

Odległość między krawędzią podpory lub obwodem powierzchni obciążonej i najbliższym uwzględnianym w obliczeniach zbrojeniem na ścinanie nie powinna przekraczać d/2. Odległość tę należy odmierzać na poziomie zbrojenia rozciąganego. Jeśli stosuje się tylko pojedynczą linię prętów odgiętych, to ich nachylenie można zmniejszyć do 30°.

Na ostatnim obwodzie o promieniu $r_s$  rozstaw strzemion $s_{t,s}$ nie może przekroczyć 2d, a na mniejszych w tym $u_1$ – 1,5d. Stąd liczba strzemion nie powinna być mniejsza niż:

$n_{t,s}=u_s/2 d$ na ostatnim (najdalej oddalonym obwodzie $u_s=2\pi r_s$

$n_{t,1}/(1,5d)$ na obwodach mniejszych (mniej oddalonych od słupa)

Z układu warunków:  $(\ref{28})$, $(\ref{30})$, oraz minimalnej liczby strzemion na obwodzie wynika, że  średnica strzemion może być wstępnie określona z formuły

$$\begin{equation} \Phi \ge \sqrt{\dfrac{A_{sw} }{\pi n_t}}  \label{31} \end{equation}$$

choć nie jest on bezwzględnie obowiązujący, ponieważ liczba kombinacji możliwego zbrojenia i średnic powinna być optymalnie dobrana, ale tak by spełniała podane wcześniej warunki wytrzymałościowe i konstrukcyjne.

Wytrzymałość przekroju ze zbrojeniem na ścinanie przez przebicie

Przekrój zbrojony na przebicie klasycznie (strzmiona , pręty odgiete)

Jeśli przekrój płyty został zazbrojony na ścinanie stalą o przekroju $A_{sw}$, sposobami opisanymi niżej , to jego wytrzymałość wzrasta do:

$$\begin{equation}v_{Rd,cs} =  0,75 \cdot v_{Rdc} + 1,5  \dfrac {d} {s_r}\cdot A_{sw} \cdot f_{y,fd,ef} \cdot \dfrac{sin\alpha}{A_1}  \label{32} \end{equation}$$

gdzie:

$v_{Rd,c}$  – wnośność betonu nie zbrojonego na ścinanie  którą wyznacza się  z formuły  (13) {ŚSBŻ]

W formule $(\ref{32})$  pole  $A_1=u_1\cdot d$ jest polem przekroju betonu w podstawowym obwodzie kontrolnym $u_1$ (dla $x=2d$).

Przekrój zbrojony  na przebicie specjalnymi wkładkami patentowymi

Wytrzymałość przekroju na ścinanie przez przebicie, zbrojowego specjalnymi wkładkami patentowymi : Extrea, Filigran, Halfen, Peikko, Schöck,i innymi

wyznacza się z prostej zależności:

$$\begin{equation}v_{Rd,cs} =  \alpha _{max}  \cdot v_{Rdc} \label{33} \end{equation}$$
gdzie:

$\alpha _{max}$ – współczynnik zwiększenia nośności w stosunku do betonu bez zbrojenia na ścinanie,  który podaje producent wkładek zbrojenia na ścinanie przez przebicie.

Przykładowe zwiększenia nośności podawane przez producentów wynoszą:

Peikko [7]
płyty stropowe  $\alpha_{max} = 1,96$
płyty oraz stopy fundamentowe stropowe  $\alpha_{max} = 1,62$

Halfen [8]
płyty stropowe  $\alpha_{max} = 1,96$
Dla porównania skuteczność tradycyjnego zbrojenia strzemionami wynosi  $\alpha_{max} = 1,4$

Przykłady rachunkowe

Załącznikiem do przykładów jest arkusz kalkulacyjny Przebicie.

Przykład 1 [Zbrojenie strzemionami wokół słupa wewnętrznego]

Przykład [9].,Example 3.4.10

Dobrać indywidualne zbrojenie strzemionami, na przebicie płyty, wokół słupa wewnętrznego w układzie usztywnionym (\beta=1,15) z detalem pokazanym na  rys. 16 .

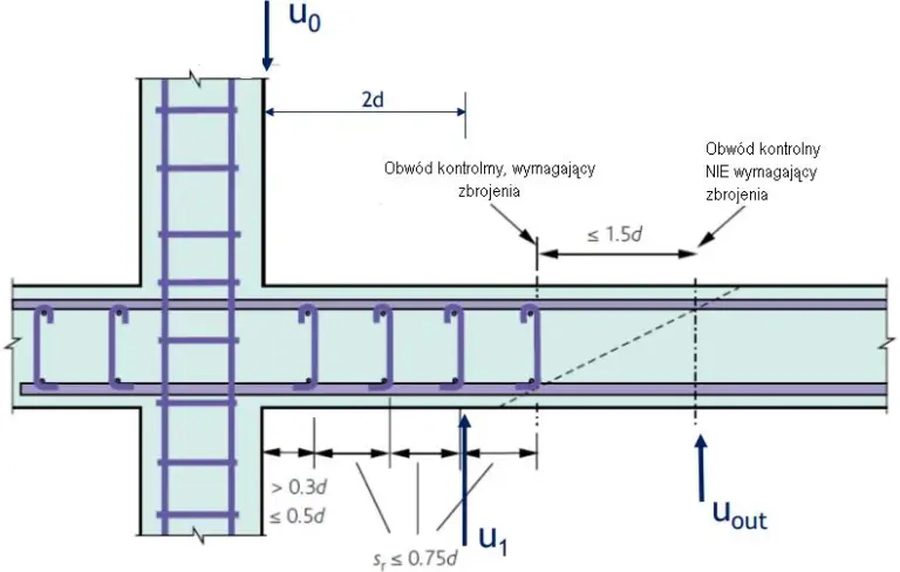
Rys.16 Detal płyta-słup do przykładu [10]

Dane i wyniki ogólne

Słup wewnętrzny o wymiarach $c_y=400\, mm $, $c_z=400 \, mm$,

rys. 3 $\to $ współczynnik mimośrodów dla słupa wewnętrznego $\beta=1,15$

Płyta: grubość $h=300 \, mm$,; otulenia: $a_y=40$ mm, $a_z=60 mm$ ;  wysokości użyteczne:  $d_y=$ 260 mm , $d_z=$ 240 mm,
$d=(260+240)/2=250 \, mm$,

Beton: C30/37  $f_{ck}=30$ MPa , $f_{cd}=1,0 \cdot 30/1,4=21,4$ MPa,

Stopień zbrojenia podłużnego na zginanie  $\rho_y=0,0085$, $\rho_z=0,0048$, $\rho=\sqrt {0,0085\cdot 0,0048}=0,0064$

Obciążenia

obliczeniowa reakcja słupa  dolnego $V_{Ed}^d$ = 2215,0 kN,
obliczeniowa reakcja słupa górnego  $V_{Ed}^g$ =1010,2 kN

obciążenie równomiernie rozłożone stropu:

charakterystyczne:
$G_k=6,2 \, kN/m^2$  – ciężar stropu, warstwy wykończeniowe  oraz inne stałe,
$Q_{u,k}=3,5 \,  kN/m^2$ – obciążenie użytkowe,
$Q_{ś,k} =0,8 \,  kN/m^2$ – , zastępcze obciążenie ściankami działowymi,
$Q_{p,k}=0,5 \, kN/m^2$ –  obciążenie instalacjami podwieszonymi,

obliczeniowe:
$Q_d=1,15\cdot 6,2+1,5(1\cdot3,5+0,7\cdot 0,8 + 0,7\cdot0,5)=15,0  \, kN/m^2$

Maksymalna wytrzymałości betonu na ścinanie przy przebiciu
($\ref{12}) \to$ dla betonu C30/37 $v_{Rd,max}= 0,24 \cdot 30/1,4 \cdot (1-30/250) = 4,53 \, MPa$

Wytrzymałość  betonu nie zbrojonego na ścinanie

(13) {ŚSBŻ] $\to$
$v_{Rd,c}=max\left[ (0,129 \cdot 1,89 \cdot (100 \cdot 0,0064 \cdot 30)^{1/3} \, ; \, 0,50 \right] =0,652 \, MPa$., gdzie:
pod  (13) {ŚSBŻ] $\to$
$C_{Rd,c}=0,129$
$k=min[1+\sqrt{200/250}/ ; 2,0]=1,89$,
$\nu_{min}= 0,035 \cdot 1,89^{3/2} \cdot 30^{1/2}=0,50$,

Sprawdzenie ścinania  w licu słupa (na obwodzie $u_0$)

Siła przebijająca obwód $u_0$
rys.4  wewnątrz  obwodu wokół słupa  nie uwzględniamy obciążenia rozłożonego)
($\ref{11}$) $\to$ $V_{Ed,0}=V_{Ed,red} = 2215-1010,2=1204,8 \, kN$

Obwód słupa $u_0=2 \cdot(c_y+c_z)= 2\cdot(400+400)=1600$ mm

Warunek wytrzymałości  na obwodzie $u_0$) wokół podpory – na zmiażdżenie betonu:

($\ref{9}) \to $ $v_{Ed,0} = 1,15\cdot 1204,8/(1600 \cdot 250)\cdot 10^3=3,46 \, < \, 4,53 \, MPa$

Warunek  jest spełniony, więc nie jest potrzebna zmiana wymiarów słupa lub grubości płyty.

Położenie obwodu krytycznego x_max

Ponieważ na powierzchni płyty w obszarze przebicia ( 0<x $\le 2d$) działa równomierne obciążenie $Q_d$ korzystnie redukujące siłę przebijającą słupem dolnym, więc maksimum wytężenie dla betonu niezbrojonego może wystąpić dla $x_{max}$. Poszukiwanie $x_{max}$ przeprowadzono w arkuszu kalkulacyjnym „Przebicie.xls” – pierwsza zakładka „1 Prosto. wewn.”

W wyniku uzyskano $x_{max}=867 $ mm, czyli poza obwodem podstawowym $(x=2d=2\cdot 250=500$ mm.

Oznacza to, że obwodem krytycznym jest obwód podstawowy $u_1= u{2d}$ i w tym obwodzie prowadzono dalsze analizy.

Sprawdzenie ścinania na podstawowym obwodzie kontrolnym $u_1 =u_x (x=2d)$

Podstawowy obwód kontrolny  dla $x=2d= 2\cdot250=500 \, mm$
($ \ref{15}$)  $\to$ $u_1= u_x (2d) = 2 ( 400 + 400 +2 \pi \cdot 500) =4742$ mm

rys.4  $\to$
pole obciążenia rozłożonego wewnątrz obwodu $u_1$  $A_{q1}=[2 \cdot 500 (400+400) +\pi \cdot 500^2] \ /10^2=15854\, cm^2$
siła przebijająca $V_{Ed,1}= 2215/ – 1010,2 – 15,0 \cdot 15854 \cdot 10^{-4}=1204,8-23,8 =1181 \, kN$

warunek wytrzymałosci  na obwodzie podstawowym $u_1$:
$(\ref{10}$) , $(\ref{9}$) $v_{Ed,1}=1,15 \cdot 1181 / (4742 \cdot 250) \cdot 10^3=1,15 \, > \,  0,652 \, MPa$.

Ponieważ na obwodzie podstawowym$ u_1$  nie jest spełniony warunek wytrzymałości przekroju nie zbrojonego na ścinanie więc zbrojenie  jest wymagane.

Rozmieszczenie zbrojenia

• Skrajny obwód kontrolny $u_{out}$ , gdzie beton nie zbrojony ma już wystarczającą nośność

$( \ref {27})$ $\to$
długość    $u_{out}= 1,15 \cdot 1181 /(0,652 \cdot 250 ) \cdot 10^3= 8335 $ mm,
promień $ r_{out}=8335 / (2 \pi)= 1327 $ mm (od środka słupa licząc)

• Skrajny obwód zbrojenia $u_s$ powinien być umieszczony o $k\cdot d=1,5d$ wgłąb obszaru objętego obwodem $u_{out}$, czyli:

promień $r_s=1327 -1,5\cdot 250=952$ mm,

długość  $u_s =2\cdot \pi \cdot 952=5979 $ mm,

maksymalny rozstaw strzemion na tym obwodzie $ max \, t_s=2d=2 \cdot 250= 500$ mm

na obwodzie skrajnym szacunkowo należy dać strzemiona w liczbie  $n_{ts}=5979/500+1=13$,

rzeczywisty rozstaw strzmion $t_s=5979/13=461$ mm

• Pierwszy (najbliższy słupa) obwód zbrojenia powinien być oddalony max 0,5 d od lica słupa, czyli:

promień $r_{0,5d}=c/2+0,5d=400/2+0,5\cdot 250=325$ mm,

długość $u_{0,5d}=2\cdot \pi \cdot 325=2042$ mm

liczba strzemion (min rozstaw 1,5d)
$n_{t,05d}=2042/(1,5\cdot 250)+1=7$

rzeczywisty rozstaw strzemion
$ s_{t,05d}=2042/7=292$ m

• Pomiędzy obwodem skrajnym $u_s$ oraz pierwszym $u_{o,5d} należy umieścić obwody pośrednie w rozstawie

$max t_r=0,75 \cdot 250=188$ mm, przyjęto $s_r=175$ mm

Należy dać minimum $n_r=(952-325)/175 = 4$ obwody pośrednie zbrojenia.

Szczegółowe parametry obwodów zbrojenia zamieszczono w arkuszu kalkulacyjnym „Przebicie.xls” – pierwsza zakładka „1 Prosto. wewn.”

Układ strzemion zbrojenia na ścinanie przez przebicie pokazano na rys. 17. 

Rys.17 Układ strzemion zbrojenia na ścinanie przez przebicie wg przykładu 1

Przekrój zbrojenia na ścinanie

Stal: B500 $ f{yk}= 500 \, MPa$, $f_{yd}= \cdot 500/1,15=435 $ MPa,

Wytrzymałość stali strzemion $(\ref{29} )\to$  $f_{ywd,ef} = (250 + 0.25d) = 250+0,25\cdot250 =312,5 $ MPa.

Wymagane zbrojenie jednego obwodu kontrolnego

$(\ref{28} ) \to $ $A_{sw} \ge  \dfrac{1,15-0,75 \cdot 0,652}{1,5\cdot 312,5 \cdot 1,0 / (175 \cdot 4742)} \cdot 10^{-2}= 13,0 \, cm^2 $ /obwód

Przyjęto 18#10 ( A=14,2 cm²),

Przekrój jednego pręta $A_{s1}= 0,79 \, cm^2$

Sprawdzenie minimalnego przekroju jednego ramienia strzemiona

$(\ref{30})$ $\to$ $ A_{s1,min}=  \cfrac {1,5 \cdot sin 90^0 + cos 90^0}{175/10 \cdot 375/10} = 0,0018 >  0,08 \cfrac{\sqrt{25}}{300}=0,0009$,  czyli warunek jest spełniony.

Przykład 2 [Słupy brzegowe i narożne]

[11]dostosoweany do reguł EC2

Sprawdzić przebicie płyty stropowej na poz, 1 przez słupy brzegowe i narożne pokazane na rys.18. 

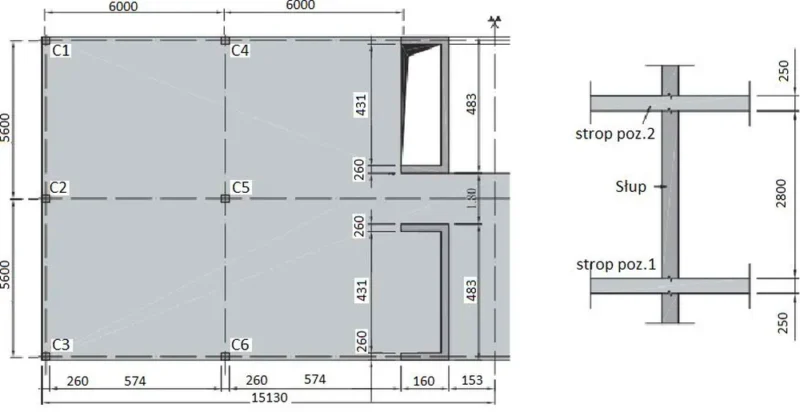
Rys. 19 Plan płyty i przekrój przez kondygnację do przykładu 3 [11]dostosoweany do reguł EC2

Dane

Wymiary słupów $c_y=260 \, mm$; $c_z=260 \, mm$

Grubość płyty : $h=250 \, mm$

Otulenie osiowe  $a=50 \to$ wysokość użyteczna $d=250- 50=200 \, mm$

Stopień zbrojenia podłużnego na zginanie  $\rho_y=0,0105$ , $\rho_z=0,0097$; $\rho_l=\sqrt {0,0105 \cdot 0,0097}=0,0101 <0,02$,

Beton C30/37: $f_{ck}=30 \, MPa$ ; $f_{cd}=30/1,4=21,4 \, MPa$

Wytrzymałość betonu na ścinanie

Wytrzymałość maksymalna betonu ( z przykładu 1)

$v_{Rd,max}=4,53 $ MPa

Wytrzymałość betonu niezbrojonego na ścinanie

(13) {ŚSBŻ] $\to$
$v_{Rd,c}=max\left[ (0,129 \cdot 2,0 \cdot (100 \cdot 0,0101 \cdot 30)^{1/3} \, ; \, 0,542 \right] =0,801 \, MPa$,
gdzie: $k=min[1+\sqrt{200/200}/ ; 2,0]=2,0$, $\nu_{min}= 0,035 \cdot 2^{3/2} \cdot 30^{1/2}=0,542$

Obciążenia

Słupy są przegubowo połączone ze stropem 1 , więc nie występują momenty zginające. Z rozwiązania statyki uzyskano następujące wartości reakcji słupów pod stropem poz.1:

• słup narożny C1, C3

$V_{Ed}^d= 93$  kN.

• słup brzegowy  C2  – 265 kN ; C4, C6 – 244$  kN

$V_{Ed}^d= 265$  kN

Równomiernie  rozłożone obciążenie : $G_k=8,3 \, kN/m^2 $,  $Q_{k,u} =3,0 \, kN/m^2$,

Q_d=$1,35\cdot 8,3+1,5\cdot 3,0= 15,7 \, kN/m^2$.

System konstrukcyjny płytowo-słupowy jest usztywniony – współczynniki nierównomierności $\beta$ są odczytywane z rys, 3, czyli:

dla słupa narożnego C1, C3: $\beta=1,5$,

dla słupów brzegowych C2, C4, C5, C6:  $\beta=1,4$

Nie występują słupy na płycie  stropu, więc
$V_{Ed}^g=0$

Obwód wokół słupa $u_0$

Długość zredukowanych obwodów kontrolnych $(\ref{15})$ oraz naprężenia $(\ref{9})$  w licu słupów, wynoszą:

• słup narożny C1, C3

$u_0=3 \cdot200=600 \le (c_y+c_z)=260+260=520 \to u_0=520 \, mm$,

$v_{Ed,0} =1,5\cdot 93/(520\cdot 200)\cdot 10^3=1,34 <4,52 \, MPa $

• słup brzegowy C2, C4, C5, C6

$u_0=260+3\cdot 200=860  \le (260+2\cdot 260)=780 \to u_0=780 \, mm $,

$v_{Ed,0} =1,4\cdot 265/(780 \cdot 200)\cdot 10^3=2,38 <4,52 \, MPa $

Warunki nośności w licu słupów ($\ref{9}$) są zachowane

Obwód krytyczny $u_{cr}$

Poszukiwanie $x_{cr}$ przeprowadzono w arkuszu kalkulacyjnym „Przebicie.xls” – zakładka ” 2 Brzegowe”. W wyniku uzyskano:

dla słupa narożnego $x_{cr}=x_{max} =209 \, mm$,

dla słupa brzegowego $x_{cr}=x_{max}=386 \,mm$.

Obwód krytyczny:

dla słupa narożnego  $u_{cr}=x_{cr} = c_y+c_z+\pi x_{cr} /2 =260+260+\pi 209/2= 848 \, mm$

dla słupa brzegowego  $u_{cr}=x_{cr} = 2(c_y+c_z)+\pi x_{cr} /2 =2(260+260)+\pi 209= 2252 \, mm$

Pole obciążenia równomiernego, ograniczone obwodem $u_cr$

dla słupa narożnego  $A_{q, cr}=[(x_{cr}(c_z+c_y+x_{cr})-x_{cr}^2 (1-PI()/4))/4]/100=[209 (260+260+209)-209^2 (1-\pi/4)/4]/100=1500 \, cm^2$

dla słupa brzegowego $A_{q, cr}=[(x_{cr}(c_z+2c_y+x_{cr})-x_{cr}^2 (1-PI()/4))/2]/100=386 (260+2\cdot 260+386)-386^2 (1-\pi/4)/2]/100=4560 \, cm^2$

Siła skupiona od obciążenia rozłożonego i zredukowana siła przebijająca

dla słupa narożnego  $V{Q,max}=15,7 cdot 1500 \cdot 10^{-4}=2,4 \, kN$,  $V_{Ed,red}=93-2,4=90,6 \, kN$

dla słupa brzegowego $V{Q,max}=15,7 cdot 4560 \cdot 10^{-4}=7,2 \, kN$,  $V_{Ed,red}=265-7,2=257,8 \, kN$

Naprężenie w obwodzie krytycznym

dla słupa narożnego  $v{Ed,max}=1,5 \cdot 90,6/(848 \cdot200) \cdot 10^3=0,801  \le 0,801 \, MPa$

dla słupa brzegowego $v{Ed,max}=1,4 \cdot 257,8 /2252 \cdot200) \cdot 10^3=0,801  \le 0,801 \, MPa$

Sprawdzenie na obwodzie podstawowym nie jest wymagane, bo  w obu przypadkach uzyska się naprężenia mniejsze.

Zbrojenie na ścinanie nie jest wymagane wokół słupa narożnego oraz brzegowego.

Przykład 3 [słup okrągły z głowicą]

[12], przykład 16.3

Sprawdzić przebicie płyty stropowej podpartej na słupie z głowicą, rys. 19. 

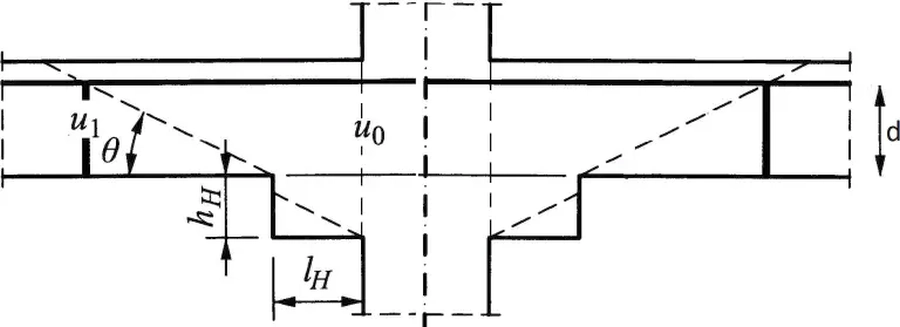
Rys.19 płyta na słupie kołowym z głowicą do przykładu 3 – zmodyfikoane [12], rys. 16.20

Dane

Słup okrągły o średnicy ø=350 mm, wewnętrzny w układzie  nieprzesuwnym $\to \beta=1,15$

Średnia wysokość użyteczna d=165 mm

Grubość głowicy $h_H=120 \, mm$

Wysięg głowicy $l_H=200 \, mm$

Obliczeniowa siła w słupie $V_{Ed}=520 \, kN$

Beton C20/25 $f_{ck}=20 \, MPa$;  $f_{cd}=20/1,4=14,3 \, MPa$

Zbrojenie płyty na zginanie: $ A_{sy}=A_{sz}= Φ12/20-250 = 29,66 \, cm^2$; $\rho_l=29,66/(100\cdot16,5)=0,018 <0,2$

Wytrzymałość betonu na ścinanie

Maksymalna wytrzymałość na ścinanie

($\ref{12}) \to$ dla betonu C20/25 $v_{Rd,max}= 0,24 \cdot 20/1,4 \cdot (1-20/250) = 3,15 \, MPa$

Wytrzymałość na ścinanie przekroju niezbrojonego

(13) {ŚSBŻ] $\to$
$v_{Rd,c}={max [ \tfrac{0,18}{1,4} \cdot 2 \cdot (100 \cdot 0,018 \cdot 20^{1/3}+0) \, ; \, (0,44 +0)] }=0,85 \, MPa$, gdzie:
$k=min \{1+\sqrt {200/165} ; 2,0 \}=2,0$,
$\nu_{min}= 0,035 \cdot 2^{3/2} \cdot 20^{1/2}$=0,44 \, MPa,
$k_1\cdot \sigma_p=0$

Obwody kontrolne

Obwód wokół słupa $u_0=\pi\cdot 350=1100 \, mm$

Obwód podstawowy

dla płyty bez głowicy $u_1= \pi \cdot(350+4 \cdot165)=3173 \, mm$

dla płyty z głowicą $u_1=\pi\cdot (350+2 \cdot 200+4 \cdot165)=4430 \, mm$

Naprężenia ścinania oraz warunki wytrzymałościowe

$v_{Ed,0} =  \dfrac{1,15 \cdot 520} {1100 \cdot (165+120)} \cdot 10^3=1,91 \le  3,16  \, MPa \to $ nie potrzeba korygować szalunków

$v_{Ed,1} =  \dfrac{1,15 \cdot520}{4430 \cdot 165} \cdot 10^3=0,82 \le  0,85 \, MPa \to $ płyty nie trzeba zbroić na ścinanie przez przebicie

Przykład 4 [Płyta z otworami obok słupa]

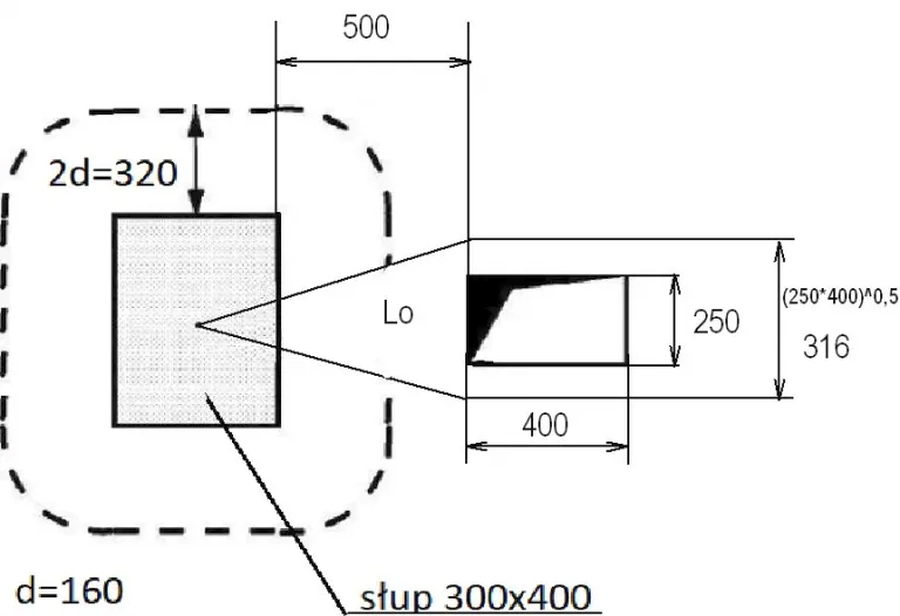
Sprawdzić przebicie przez słup  płyty z otworem . Na rys. 20 pokazano fragment płyty z lokalizacją otworu.

Rys .20 Fragment płyty z otworem do przykładu 5

Dane i wyniki ogólne

Słup prostokątny  $c_y=300 \, mm$ , $c_z= 400\, mm$, wewnętrzny w układzie  usztywnionym $\to \beta=1,15$

Płyta ze średnią wysokością użyteczną (efektywną)  d=160 mm

Beton C25/30: $f_{ck}=25 \, MPa$;  $f_{cd}=25/1,4=17,9 \, MPa$, zbrojony na zginanie $\rho_l=0,018$

Otwór $l_1 \times l_2= 400 \times 250$ oddalony o 500 mm od krawędzi słupa

Obliczeniowa siła w słupie $V_{Ed}=600,3 \, kN$

Wytrzymałości na ścinanie

($\ref{12}) \to$ dla betonu C25/30 $v_{Rd,max}= 0,24 \cdot 25/1,4 \cdot (1-25/250) = 3,86 \, MPa$

(13) {ŚSBŻ] $\to$
$v_{Rd,c}=max\left[ (0,129 \cdot 2 \cdot (100 \cdot 0,018 \cdot 25)^{1/3} \, ; \, 0,495\right] =0,495 \, MPa$, gdzie:
$k=min[1+\sqrt{200/160}/ ; 2,0]=2,0 $,
$\nu_{min}= 0,035 \cdot 2,0^{3/2} \cdot 25^{1/2}=0,495$,

Obwody kontrolne

Obwód $u_0$ wokół słupa $u_0= 2(300+400)=1400 \, mm$

Obwód podstawowy $u_1$

współrzędna $x_1=2d=2\cdot160=320 \, mm$

długość obwodu bez redukcji ze względu na otwór $u_1=2\cdot(300+400+\pi 320)=3411 \, mm$

odcinek redukcji przez otwór $(\ref{19})$

$L_o=316 \cdot (300/2+320)/(300/2+500)=229 \, mm$, gdzie

gdzie szerokość zastępcza otworu $s_O=\sqrt{300\cdot 400}=316 \, mm$

zredukowany obwód podstawowy $u_1^*$

$u_1^* = 3411-229=3182 \, mm$

Naprężenia ścinające i nośność

$v_{Ed,0} =  \dfrac{1,15 \cdot 600} {1400 \cdot 160} \cdot 10^3=3,08 \le 3,86 \, MPa$ $\to$  zmiana wymiarów szalunków nie jest potrzebna

$v_{Ed,1} =  \dfrac{1,15 \cdot 600,3}{3182 \cdot 160} \cdot 10^3=1,36 > 0,495 \, MPa$ $\to$  ,

więc płytę należy zbroić na ścinanie wokół słupa. Sposób doboru zbrojenia pokazano w przykładzie 1

Przykład 5 [przebicie stopy fundamentowej]

[13], pkt 8.3.

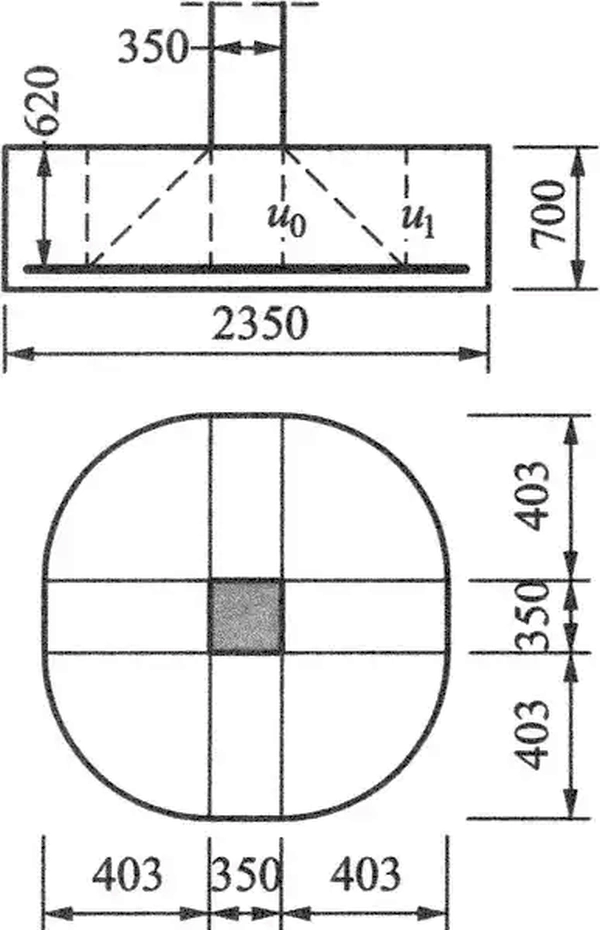
Sprawdzić przebicie stopy fundamentowej, pokazanej na rys. 21

Rys. 21 Stopa fundamentowa do przykładu 5

Dane i wyniki ogólne

Słup prostokątny  $c_y=350$ mm, $c_z= 350$ mm , wewnętrzny w układzie  usztywnionym $\to \beta=1,15$

Wymiary stopy fundamentowej $A_f=2350$ mm,   $B_f=2350$ mm $H=700$ mm

Wysokość użyteczna stopy d=620 mm

Beton C25/30, zbrojony na zginanie $\rho_l=0,018$ ; Stal B500.

Wytrzymałości betonu na ściskanie i ścinanie wg przykładu 4.

Obciążenia

Obliczeniowa siła w słupie $V_{Ed}=2204 \, kN$ ( Uwaga: bez uwzględnienia ciężaru stopy i obciążenia powierzchniowego stopy)

Powierzchnia rozkładu odporu  $(\ref{25})$:

$a_f=min \, [ (c_y+5 h_f)=350+5\cdot 700 \, ; \, 2350 \,=2350$ mm
$b_f=min \, [ (c_z+5 h_f)=350+5\cdot 700 \, ; \, 2350 \,=2350$ mm

$ A_{Q,f}2,35 \cdot 2,35=5,52 \, m^2$

Naprężenia pod fundamentem

$Q_f=2204/5,52=399,3 \, kN/m^2$

Obwód kontrolny $u_0$

Obwód $u_0$ wokół słupa $u_0= 4 \cdot 350=1400 \, mm$

$v_{Ed,0} =  \dfrac{1,15 \cdot 2204} {1400 \cdot 620} \cdot 10^3=2,92 \le 3,86 \, MPa$ $\to$  zmiana wymiarów szalunków nie jest potrzebna

Obwód krytyczny $u_{cr}$

Poszukiwanie położenia obwodu krytycznego $x_{max}$ przeprowadzono w arkuszu kalkulacyjnym „Przebicie.xls” – zakładka „5 Stopa fundamentowa”

Wynik $x_max = 454$ mm

Długość obwodu krytycznego $u_{max}=2\cdot(350+350+\pi 454=4251 \, mm$

Powierzchnia wewnątrz obwodu krytycznego $A_{qx}==(2*(350+350)\cdot 454+\pi 454^2+350\cdot350 )/100=14046 \, cm^2$

Siła odporu wewnątrz obwodu krytycznego  $V{Qf}=399,3\cdot 14046/10^{-4}=560,6 \, kN$

Zredukowana siła przebijająca $V_{Ed,red}=2204-592,6=1643,4 \, kN$

$v_{Ed,max} =  \dfrac{1,15 \cdot 1643,4}{4251 \cdot 620} \cdot 10^3=0,717 \le  0,717 \, MPa$ $\to$  stopy nie trzeba zbroić na ścinanie

Przykład 6 [przebicie płyty fundamentowej]

[12], Przykład 16.5

Sprawdzić przebicie płyty fundamentowej o wymiarach pola: długość 12 m, szerokość 24 m, grubość 800 mm,

obciążonej prostokątnym słupem wewnętrznym 250×700 mm w układzie usztywnionym.

Dane i wyniki ogólne

Słup prostokątny  $c_y=700$ mm, $c_z= 250$ mm , wewnętrzny w układzie  usztywnionym $\to \beta=1,15$

Płyta fundamentowa:

grubość $h_f =800 \, mm$

wysokość użyteczna: $d_y=738 \, mm$ , $ d_z=713 \, mm$, średnia $d=(738+713)/2=725 \, mm$

beton C30/37, zbrojony na zginanie:  $\rho_{ly}=0,0831$ , $\rho_{lz}=0,0043$ , średni $\rho_l=\sqrt{0,83 \cdot 0,0043}=0,0189  \le 0,02$

Wytrzymałość betonu na ścinanie

Maksymalna wytrzymałość betonu C30/37 na ścinanie

$v_{Rd,max}=4,53$ MPa (wg przykładu 1)

Wytrzymałość betonu niezbrojonego  na ścinanie
(13) {ŚSBŻ] $\to$
$v_{Rd,c}=max\left[ (0,129 \cdot 1,53 \cdot (100 \cdot 0,0189 \cdot 30)^{1/3} \, ; \, 0,361  \right] =0,753 \, MPa$., gdzie:
$C_{Rd,c}= 0,129$,
$k=min[1+\sqrt{200/725}/ ; 2,0]=1,53$,
$\nu_{min}= 0,035 \cdot 1,53^{3/2} \cdot 30^{1/2}=0,361$,

Obciążenia

Obliczeniowa siła w słupie $V_{Ed}=3500 \, kN$ ( Uwaga: bez uwzględnienia ciężaru stopy i obciążenia powierzchniowego stopy)

Powierzchnia rozkładu odporu  $(\ref{25})$:

$a_f=c_y+5 h_f=700+5\cdot 800 =4700$ mm
$b_f=c_z+5 h_f=250+5\cdot 800 =3750$ mm

$ A_{Q,f}4,70 \cdot 3,75=17,63 \, m^2$

Naprężenia pod fundamentem

$Q_f=3500/17,63=198,5 \, kN/m^2$

Obwód kontrolny $u_0$

Obwód $u_0$ wokół słupa $u_0= 2(700+250)=1900 \, mm$

$v_{Ed,0} =  \dfrac{1,15 \cdot 2204} {1900 \cdot 725} \cdot 10^3=2,92 \le 3,86 \, MPa$ $\to$  zmiana wymiarów szalunków nie jest potrzebna

Obwód krytyczny $u_{cr}$

Poszukiwanie położenia obwodu krytycznego $x_{max}$ przeprowadzono w arkuszu kalkulacyjnym „Przebicie.xls” – zakładka „6 Płyta fundamentowa”

Wynik $x_max = 870$ mm

Długość obwodu krytycznego $u_{max}=2\cdot(250+700+\pi 870)=7369 \, mm2$

Pole powierzchni zawarte wewnątrz $u_{max} $A_{q,max}=42087 \, $ cm^2

Siła odporu wewnątrz obwodu krytycznego  $V{Qf}=198,5 \cdot 42087/10^{-4}=737,4 \, kN$

Zredukowana siła przebijająca $V_{Ed,red}=3500-737,3=2762,7 \, kN$

$v_{Ed,max} =  \dfrac{1,15 \cdot 2762,7}{7369 \cdot 725} \cdot 10^3=0,753 \le  0,753 \, MPa$ $\to$  stopy nie trzeba zbroić na ścinanie

Przykład 7 [Zbrojenie systemowymi bolcami]

Rozwiązania systemowe zbrojenia bolcami dobiera się z wykorzytaniem programów obliczeniowych dostarczanych przez producentów systemów.

Przykładem jest program Peikko-Designer konsorcjum Peikko Group, który można pobrać i zainstalować ze strony

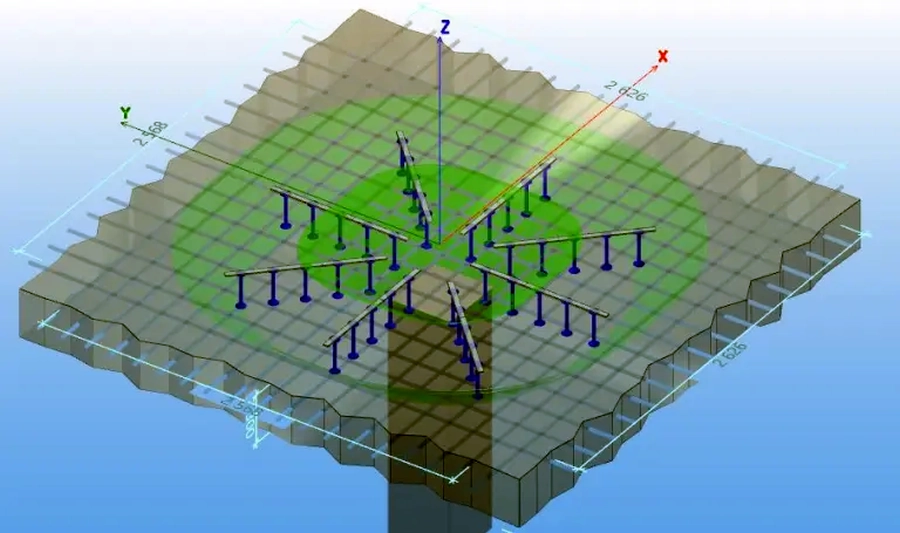
Na rys. 22 pokazano obraz zbrojenia kołkami dwugłowymi Peikko PSB dla danych z przykładu 1. 

Rys.22 Diagram z programu Peikko Designer , moduł „Punching Reinforcement”

Firma HALFEN udostępnia oprogramowanie na Software HALFEN .

Wymiarowanie zbrojenia bolcami dwugłowymi jest prowadzone według Europejskiej Aprobaty  ETA-13/0136.

Znane jest i stosowane wiele systemów zbrojenia bolcami. Gwarantują one bezpieczeństwo połączeń i sprawność montażu, ale zwykle są droższe od indywidualnego zbrojenia strzemionami.  W związku z tym są stosowane w profesjonalnym, hurtowym wykonawstwie w przypadkach, w których ważny jest czas wykonania konstrukcji.Literatura

1. PN-EN 1992-1+AC+Ap 1,2,3:2008, Projektowanie konstrukcji z betonu -Część 1-1: Reguły ogólne i reguły dla budynków
2. CEB/fib Task Group (2001), Punching of structural concrete slabs (Technical Report No. 12)
3. Krzyś, W., Życzkowski, M. (1962). Sprężystość i plastyczność. Wybór zadań i przykładów. Państwowe Wydawnictwo Naukowe.
4. DIN EN 1992-1-1∕NA:2013-04: Nationaler Anhang – National festgelegte Parameter – Eurocode 2:Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken – Teil 1-1: Allgemeine Bemessungsregeln für den Hochbau. Beuth Verlag, Berlin, April 2013
5. PN-EN 1997-1+AC+Ap1+Ap2:2008, Projektowanie geotechniczne – Część 1: Zasady ogólne
6. Guminiak M., Analiza płyt cienkich metodą elementów brzegowych z wykorzystaniem nowego sformułowania warunków brzegowych, Rozprawa doktorska , Wydawnictwo Politechniki Poznańskiej, Poznań, 2004
7. Peikko, Zbrojenie na przebicie PSB®. Zbrojenie na ścinanie w konstrukcjach żelbetowych, 2020
8. Halfen , Zbrojenie nq przebicie i zbrojenie na ścinanie . Katalog techniczny, 2022
9. CH GoodChild. (2009). Worked Examples to Eurocode 2.: Volume 1. The Concrete Centre
10. MPA The Concrete Centre. (2016). Slabs and Flat Slabs. Lecture 5. EC2 Webinar – Autumn 2016. https://www.concretecentre.com/TCC/media/TCCMediaLibrary/Presentations/Lecture-5-Slabs-and-Flat-Slabs-PHG-N-Rev13-15-Oct-16.pdf
11. Lips, S., Muttoni, A., Fernández Ruiz, M. (2011). Punching of flat slabs: Design example. Lecture of  Ecole Polytechnique Fédérale de Lausanne, Switzerland, [https://ibeton.epfl.ch/MC2010Punching/NMC-Example_111215.pdf]
12. Knauff, M., Golubińska, A., & Kryziak, P. (2014)., Tablice i wzory do projektowania konstrukcji żelbetowych z  przykładami obliczeń  Wydanie drugie, PWN
13. Knauff, M., Golubińska, A., & Knyziak, P. (2015). Przykłady obliczania konstrukcji żelbetowych. Budynek ze stropami płytowo-żebrowymi. Zeszyt 1. PWN.

________________________________