Kopuły w architekturze i budownictwie są stosowane od wieków przede wszystkim jako elementy stanowiące dominanty architektoniczne budowli. Obciążenie wiatrem kopuł zależy od wielu czynników (nie tylko geometrii samej kopuły, ale również od otoczenia i sztywności konstrukcji), więc z zasady powinno być wyznaczane indywidualnie w drodze badań eksperymentalnych w tunelu aerodynamicznym lub z użyciem symulacji numerycznych. Podczas projektowania wstępnego konstrukcji kopuły można stosować zalecenia normy [1].
Niniejszy artykuł wychodzi naprzeciw pytań projektantów, wynikających z trudności interpretacyjnych nowych zasad i praktycznie zupełnym brakiem przykładów wyznaczania obciążenia kopuł.
Artykuł dotyczy kopuł o najprostszym kształcie: sfery kulistej na rzucie kołowym. W przypadku kopuł o bardziej złożonym kształcie badania modelowe są obowiązkowe. Każdą kopułę traktujemy indywidualnie, choć przy projektowaniu wstępnym zaleca się aproksymować kopułę fragmentami czaszy kulistej i dla nich wyznaczać współczynniki ciśnienia, a także stosować analogie do dachów wielospadowych, pilastych itp.
Współczynniki ciśnienia na powierzchnię kopuły
Specyfika wyznaczania obciążenia kopuł zgodnie z normą [1] polega na wyznaczaniu współczynnika ciśnienia zewnętrznego $C_{pe}$, który dla kopuł sferycznych o średnicy $d$ na rzucie koła, posadowionych na budynku o wysokości $h$ i o strzałce uwypuklenia $f$ jest pokazany na rys. 1.
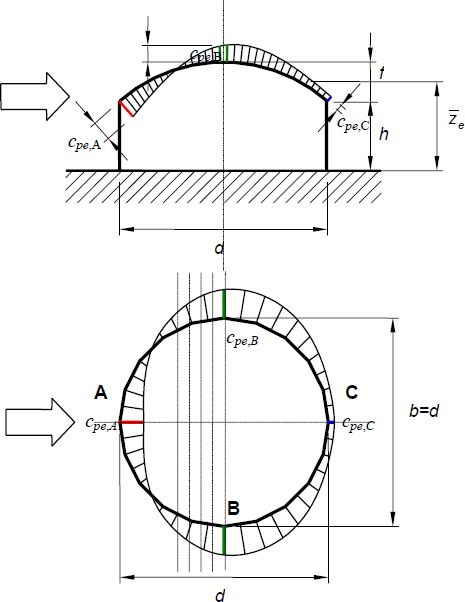
Rys. 1. Obciążenie wiatrem kopuły sferycznej. proporcjonalne do współczynnika ciśnienia zewnętrznego Cpe [2]
Współczynnik ciśnienia zewnętrznego
Współczynnik ciśnienia zewnętrznego $C_{pe}$ jest współczynnikiem proporcjonalności ciśnienia (p)=(pressure) wiatru na powierzchni zewnętrznej (e)=(external).
Zalecany przez [1] rozkład obciążenia wiatrem polega na przyjęciu, że na łuku kopuły wyznaczonej przez przecięcie pionową płaszczyzną prostopadłą do kierunku wiatru ciśnienie jest stałe (linie kropkowe na rys.1)
Przyjmuje się, że współczynnik ciśnienia zobrazowany na rys.1 może być używany do analizy całości budowli(kopuły), czyli jest współczynnikiem globalnym, uzyskiwanym przez uśrednienie punktowych współczynników na powierzchni 10 m2: $C_{pe}= C_{pe,10}$. W przypadku oddziaływań lokalnych należy brać współczynnik uśredniony na powierzchni $1 m^2$, który oznaczamy innym indeksem: $C_{pe,1}$.
Wartości współczynnika ciśnienia na ustalonym łuku prostopadłym do kierunku wiatru należy wyznaczyć z interpolacji współczynników $C_{pe,A}$, $C_{pe,B}$ i $C_{pe,C}$ odpowiednio dla punktów A, B i C, oznaczanych na rys. 1 i położonych w strefie nawietrznej (A), środkowej (B) i zawietrznej C. Proponujemy, by interpolację wykonać następującą techniką:
| $C_{pe,X}=C_{pe,A} + (C_{pe,A}-C_{pe,B}) \cdot \dfrac {2x}{d}$ | (1a) |
| $C_{pe,X}=C_{pe,B} + (C_{pe,B}-C_{pe,C}) \cdot \dfrac {2x}{d}$ | (1b) |
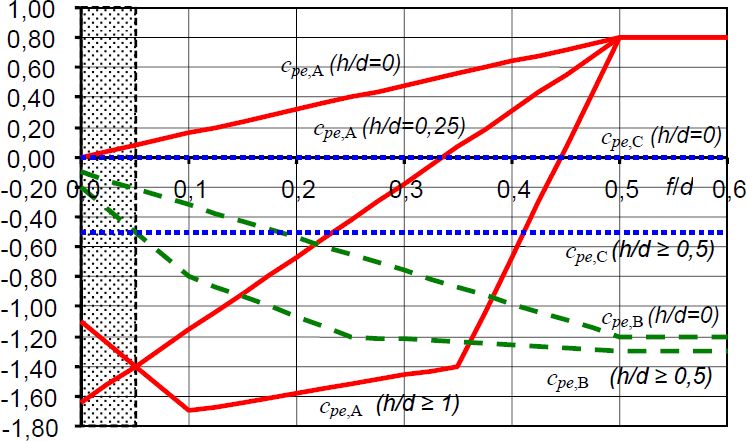
Rys.2. Wartość współczynników C{pe,i, (i=A-kolor czerwony,B- kolor zielony, C – kolor niebieski) dla kopuły kołowej [2]
| $h=2,75 m$ | (1P) |
| $f=4,40 m$. | (2P) |
$\dfrac{f}{d}= \dfrac{4,40}{11,00}=0,40$
| $y=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)+y_1$ | (2) |
| $y=\dfrac{0,80 -(-1,65}{0,5-0,0}(0,4-0,0)-1,65= 0,31$, co zapisujemy tabelarycznie |
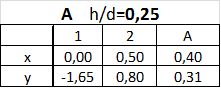
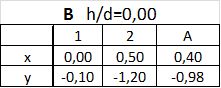
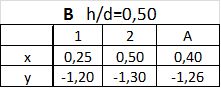
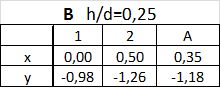
Dla punktu C z interpolacji podług $f/d$ i następnie $h/d$, mamy:

Ostatecznie współczynniki $C_{pe}$ dla $h/d=0,25$ i $f/d=0,40$ w charakterystycznych punktach kopuły, wynoszą:
w pkt A $ 0,31 $
w pkt B $ -1,18 $
w pkt C $ -0,25 $
Wartości współczynnika na łukach wyznaczymy na łukach kopuły. Z zależności interpolacyjnych (1b) i (1a) otrzymano współczynniki zestawione w tab.1. Punkty charakterystyczne A, B, C podano na tle żółtym. Na tle błękitnym podano wartości rzędnych łuku x (licząc od lewej krawędzi) i opowiadające $C_{pe}$.
Tab.1. Wartości współczynnika ciśnienia na łukach przykładowej kopuły

W obliczeniach wstępnych można przyjąć, że ciśnienie wiatru jest stałe na każdej z ćwiartek kopuły i wynosi:
na pierwszej ćwiartce (strona nawietrzna) $C_{pe}=-0,06$,
na drugiej ćwiartce (środek połaci od strony nawietrznej) $C_{pe}=-0,81$,
na trzeciej ćwiartce (środek połaci od strony zawietrznej) $C_{pe}=-0,95$,
na czwartej ćwiartce (strona zawietrzna) $C_{pe}=-0,25$.
Przy aproksymacji działania wiatru tylko na dwie połacie mamy (w tab.1. na tle białym):
na połaci nawietrznej $C_{pe}=-0,44$,
na połaci zawietrznej $C_{pe}=-0,72$.
Przy aproksymacji równomiernego ssania na całości czaszy kopuły mamy z uśrednienia w połówkach połaci:
| $C_{pe}= \dfrac{- 0,44- 0,72}{2}= – 0,38$. | (3P) |
Ten sam wynik uzyskamy uśredniając wartości w ćwiartkach.
Współczynnik ciśnienia wewnętrznego i ciśnienia całkowitego
Działanie wiatru na zewnątrz kopuły wywołuje również ciśnienie wewnątrz obiektu $C_{pi}$.
Ciśnienie wewnętrzne w odróżnieniu od zewnętrznego jest praktycznie stałe na wszystkich wewnętrznych powierzchniach i jest wywołane różnicą ciśnień chwilowego zewnętrznego i bardziej ustabilizowanego wewnętrznego. Można przyjąć, że w szczelnym obiekcie bez urządzeń wentylacji mechanicznej, ciśnienie jest stałe i ustabilizowane na poziomie ustalonym ciśnienia zewnętrznego. W tym przypadku cała różnic ciśnień lokalnych ujmuje $C_{pe}$ i współczynnik $C_{pi}$ możnaby uznać za zerowy.
Z zasady nie można jednak uznać, że konstrukcje są w pełni uszczelnione, a ciśnienie wewnętrzne zerowe. Można przyjąć, że ciśnienie $C_{pi}=0 $, gdy jest spełniony jeden z warunków:
- całkowita powierzchnia otworów nie przekracza 0,0002 ogólnej powierzchni zewnętrznej budynku,
- obiekty mają pełną i skuteczną z kontrolę otwarcia otworów (zastosowano automatykę, samozamykacze lub skonstruowano okna lub świetliki nieotwieralne).
Pod wpływem wahań ciśnienia zewnętrznego przy oczywiście stosowanych otworach uchylnych lub stałych, na skutek bezwładności filtracji obserwowane są duże różnice w zależności od rozmiarów i położenia otworów. W przypadku, gdy w budynku nie ma ściany dominującej na przenikanie wiatru i dach nie posiada więcej niż 30% otworów, a otwory sa rozmieszczone w miarę równomiernie na wszystkich przegrodach, to współczynnik ciśnienia zewnętrznego można wyznaczyć jako średnią ważoną:
| $\dfrac{A_p^2\cdot C_{pe,p}+A_n^2\cdot C_{pe,n}}{A_p^2+A_n^2}$ | (3) |
gdzie:
$A_p$ całkowita powierzchnia otworów na powierzchniach o dodatnim współczynniku ciśnienia zewnętrznego,
$A_n$ całkowita powierzchnia otworów na powierzchniach o ujemnym współczynniku ciśnienia zewnętrznego,
$C_{pe,p}$ średni współczynnik ciśnienia zewnętrznego otworów podlegających dodatniemu ciśnieniu zewnętrznemu (parciu),
$C_{pe,n}$ średni współczynnik ciśnienia zewnętrznego otworów podlegających ujemnemu ciśnienia zewnętrznemu (ssaniu).
Ponieważ w przypadku kopuł praktycznie wszystkie otwory kopuły znajdą się w obszarze ssania, to z reguły stosujemy ograniczenie powyższej formuły na przypadki, w których są trudności z jej zastosowaniem. Przyjmujemy mianowicie
| $C_{p,i}=+0,2$ lub $C_{p,i}=-0,3 $, |
(4) |
w zależności od tego, która wartość jest mniej korzystna.
Współczynnik ciśnienia całkowitego jest różnicą współczynnika ciśnienia zewnętrznego oraz wewnętrznego, to znaczy w przypadku ssania na powierzchnię zewnętrzną i wypierania powierzchni zewnętrznej oba współczynniki „sumują się (zwiększają wypadkowe ssanie).
| $C_{p}=C_{pe}-C_{pi}$ | (5) |
Wyznaczyć współczynnik ciśnienia zewnętrznego dla powłoki kopuły z przykładu 1.
Czasza kopuły zawiera mniej niż 30% otworów, a w budynku nie można wydzielić ściany dominującej na przepuszczalność wiatru.
Ponieważ zastosowanie formuły (3) nie jest miarodajne, więc przyjmujemy bardziej niekorzystną wartość z wartości granicznych (4)
$C_{pi}= + 0,2 $
Parcie na powierzchnię wewnętrzną (podniebienie kopuły) sumuje się ze ssaniem i zwiększa obciążenie wiatrem kopuły.
Współczynnik równomiernego ssania na całości czaszy kopuły oszacowano jak następuje:
| $C_{p}= – 0,38-0,20= – 0,58 $. | (4P) |
Ciśnienie oddziaływania wiatru na kopułę
Po wyznaczeniu współczynników ciśnienia zgodnie z pkt.1. – ciśnienie oddziaływania wiatru na kopułę wyznacza się standardowo wg [1], przy czym znamienne dla kopuł jest również wyznaczenie wysokości odniesienia, miarodajnej do wyznaczania obciążenia wiatrem (pkt.2.1).
Wysokość odniesienia
Wysokość odniesienia kopuł wyznacza kopuł , wynosi (CNR, (2010), Guide for the assessment of wind actions and effects on struct ures, , Report No CNR – DT 207/2008, Advisory Committee on Technical Recommendations for Construction,Roma. Italy, [ http://www.cnr.it/documenti/norme/IstruzioniCNR_DT207_2008_eng.pdf ])):
| $ \overline z_e=h+\dfrac {f}{2}$ | (6) |
gdzie: f i h wg rys.1.
Ciśnienia wiatru
Bazowa prędkość wiatru
Bazowa prędkość wiatru $v_b$ jest definiowana jako średnia 10-cio minutowa prędkość wiatru na wysokości 10 m na płaskim otwartym terenie o chropowatości $z_0 = 0,05 m$, (co odpowiada terenowi II-giej kategorii) i z okresem powrotu $T_R=50 lat$.
Przy braku odpowiednich szczegółowych analiz statystycznych, które uwzględniają miejscową szorstkość terenu, topografię i kierunek wiatru, w terenie, którego wysokość wynosi mniej niż 1500 m nad poziomem morza, bazowa prędkość odniesienia wiatru nie powinna być mniejsza od wartości podanej przez równanie :
| $ v_b =v_{b,0} \cdot C_{season} \cdot C_{dir} $ | (7) |
gdzie $v_{b,0}$ jest podstawową, bazową prędkością wiatru, która zależy od strefy obciążenia wiatrem i wysokości ponad terenem $A [m]$ – patrz (8).
Polska jest podzielona na 3 strefy obciążenia wiatrem, przy czym 80% powierzchni kraju jest położone w strefie 1. Strefa 2-ga to pas ok. 100 km na wybrzeżu Bałtyku, a strefa 3-cia to obszary górskie (pas Sudetów za Wrocławiem i pas Tatr za Krakowem). Położenie stref oraz podstawowe prędkości bazowe są dane w załączniku krajowym do normy [1]. Podstawowe prędkości bazowe, wynoszą:
| $ v_{b,0}=22\cdot [1+0,0006(A-300)] \dfrac{m}{s} $ (w strefie 1 i 3) $v_{b,0}=26 \dfrac {m}{s}$ (w strefie 2) |
(8) |
Zalecany i najbardziej niekorzystny współczynnik sezonowy wynosi:
| $C_{season}=1,0 $ |
(9) |
Współczynnik kierunkowy zależy od kierunku wiatru napierającego na budowlę i przyjmuje różne wartości zależnie od strefy obciążenia. W każdej strefie wystąpi kierunek, dla którego otrzymamy najniekorzystniejszą wartość:
| $C_{dir}=1,0 $ | (10) |
Rodzaj terenu
W przypadku braku szczegółowych analiz, uwzględniających kierunek wiatru i szorstkość oraz topografię terenu otaczającego budowlę, średnia prędkość wiatru, turbulencji intensywność i maksymalne ciśnienie prędkości, zależy od trzech parametrów: współczynnika terenu $ c_r $, długości chropowatości $ z_0 $ oraz minimalnej wysokości $ z_{min} $. Współczynniki te są oszacowane w zależności od klas terenu, opisowo skategoryzowanych w tab. 2
Tab.2. Klasy chropowatości terenu [2]
Przy braku bardziej szczegółowej oceny klasa chropowatości terenu może być przypisana stosując następujące kryteria:
- o ile nie uzasadniono innego wyboru, to domyślnie należy przyjąć teren klasy C,
- do terenu klasy D dodatkowym kryterium jest to, by w odległości 1 km od budowli, w sektorze o kącie co najmniej 30° – minimum 90% terenu jest typu oznaczonego w tabeli 2c (tzn obszary bez przeszkód …),
- teren można zakwalifikować do klasy A lub B, pod warunkiem, że obszar typu opisanego w tab. 2., występuje w promieniu co najmniej 1 km i nigdy na wysokość nie mniejszą niż 20-krotna wysokość budynku, dla każdego sektora kierunku wiatru o m in kącie 30°.
- w przypadku, gdy istnieją wątpliwości co do przypisania klasy chropowatości, należy przyjąć najbardziej niekorzystny z rozpatrywanych wariantów.
Działanie wiatru jest najmniejsze w terenie klasy A, a najbardziej znaczące w terenie klasy D.
W zależności od klasy terenu A,B,C,D ustala się kategorie ekspozycji I do V. W polskich warunkach terenowych praktycznie nie wystąpi kategoria V (przypisywana wysokim górom). W załączniku krajowym ustalono IV kategorie ekspozycji (nazwane kategoriami terenu) i przypisano je do klas z tab. 2, przy czym klasę D rozbito na dwie podklasy (dla morza i dla jeziora). W tab.3. podano kategorie ekspozycji i przypisano do nich parametry: $z_0$, $z_{min}$, $z{max}$, a także współczynniki $A_r$, $k_r$, $A_e$ i $k_e$.
Tab.3. Kategorie terenu [1]
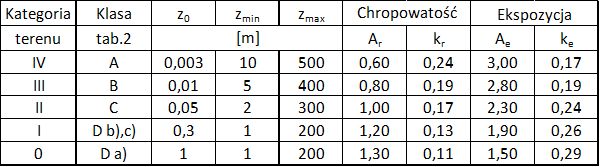
Współczynnik chropowatości lub ekspozycji terenu wyznacza się z zależności:
| $c_{\bullet} (z)=A_{\bullet} \cdot (\dfrac {\overline z_e}{10})^{k_{\bullet}} $ | (11) |
gdzie:
$\bullet$=(r – dla chropowatości, e – dla ekspozycji),
Współczynniki A i wykładniki potęgi należy przyjmować zależnie od kategorii terenu zgodnie z tab. 3.
Dla wysokości $z>z_{max}$ należy przyjmować $z=z_{max}$
W tab. 3 zamieszczono dane dotyczące $z_0$, $z_{min}$, $A_r$, $k_r$, choć nie są wykorzystywane w uproszczonej metodzie wyznaczania wartości szczytowej obciążenia wiatrem (pkt 2.2.3). Zgodnie z załącznikiem krajowym [1] do tego bezpośrednio z (11) dla $\bullet=e$. wystarcza wyznaczyć współczynnik ekspozycji $C_e$,
Ciśnienie prędkości wiatru
Wartość bazowa ciśnienia prędkości wiatru
| $q_b=\dfrac{1}{2} \rho \cdot v_b^2 $, | (12) |
gdzie:
gęstość powietrza $\rho=1,25 \dfrac{kg}{m^3}$,
Wartość szczytowa ciśnienia prędkości wiatru wynosi
| $q_p= c_e(z) \cdot q_b$, | (13) |
gdzie: współczynnik ekspozycji $c_e$ można wyznaczyć bezpośrednio z formuły(11). Wartość wyznaczona z formuły (11) podanej w załączniku krajowym różni się od wartości wyznaczonej bardziej złożoną procedurą oryginalną normy obciążenia wiatrem (w angielskiej wersji językowej). Nie jest to jednak istotne, ponieważ wartości oszacowane procedurami normowymi, różnią się systematycznie i to znacznie od ciśnienia wiatru na budynki o złożonych kształtach, w tym na kopuły, które są mierzone w tunelu aerodynamicznym lub na obiektach rzeczywistych. Dlatego autor niniejszego artykułu do analizy wstępnej poleca procedurę (11), a na etapie projektów wykonawczych sugeruje wymóg przeprowadzenia badań modelowych.
Siła oddziaływania wiatru na powierzchnię zewnętrzną
Siłę oddziaływania wiatry na powierzchnię zewnętrzną konstrukcji wyznacza się z formuły
| $F_w=c_s c_d \cdot q_p (z_e)\cdot C_p$, | (14) |
gdzie:
$c_s c_d$ – współczynnik konstrukcyjny, uwzględniający współpracę dynamiczną pod działaniem wiatru konstrukcji jako całości.
$q_p(z_e)$ – wartość szczytowa ciśnienia prędkości wiatru (10) dla wysokości odniesienia z_e.
$C_p)$ – całkowity współczynnik ciśnienia wiatru (4).
Zalecaną i bezpieczną wartością współczynniki konstrukcyjnego jest
| $c_s c_d=1,0$, | (15) |
Miarodajną wartość tego współczynnika można uzyskać wraz z wyznaczeniem $C_p$ w drodze pomiarów eksperymentalnych modeli lub obiektów rzeczywistych albo z symulacji numerycznych FDS.
Przykład rachunkowy
Wysokość odniesienia (6) wynosi:
| $ \overline z_e=2,75+\dfrac {4,4} {2}=4,95 m $ | (5P) |
Z projektu zagospodarowania terenu, wiadomo, że kopuła będzie zlokalizowana w strefie 1 obciążenia wiatrem na wysokości (A< 300 m n.p.m.) i w terenie klasy C wg tab.2, czyli w terenie kategorii II. Mamy stąd:
$v_{b,0}== 22 \dfrac{m}{s}$ (8),
$A_e=2,30$, $k_e=0,24$ (tab.3).
Współczynnik ekspozycji (11) wynosi:
| $c_e(\overline z_e)=2,30 \cdot (\dfrac {4.95}{10})^{0,24} =1,94$ | (6P) |
Wartość bazowa ciśnienia prędkości wiatru (12) wynosi:
| $q_b=0,5 \cdot 1,25 \cdot 22^2= 0,30 \dfrac {kN}{m^2}$ | (7P) |
Wartość szczytowa ciśnienia prędkości wiatru (13) wynosi:
| $q_p=q_b \cdot C_e= 0,3 \cdot 1,94=0,582 \dfrac {kN}{m^2} $ | (8P) |
Ostatecznie siła oddziaływania na powierzchnię czaszy rozpatrywanej, przykładowej powłoki sferycznej na rzucie kołowym wynosi (14):
| $F_w= 1,0 \cdot 0,582 \cdot (-0,58)=-0,338 \dfrac {kN}{m^2}$, | (9P) |
Do obliczeń numerycznych należy uszczegółowić rozkład ciśnienia wiatrem na połaci kopuły poprzez zagęszczenie stref oddziaływania (podziału kopuły na łuki równych ciśnień) zgodnie z pkt. 1.
Literatura
- PN-EN 1991-1-4:2008, Eurokod 1. Oddziaływania na konstrukcje, Część 1-4: Oddziaływania ogólne. Oddziaływania wiatru
- CNR, (2010), Guide for the assessment of wind actions and effects on struct ures, , Report No CNR – DT 207/2008, Advisory Committee on Technical Recommendations for Construction,Roma. Italy, [ http://www.cnr.it/documenti/norme/IstruzioniCNR_DT207_2008_eng.pdf ]
________________________________




