Leszek Chodor,  2 maja 2021

24-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co

Artykuł w ciągu ostatnich 24 godzin czytało 0 Czytelników

Od wczesnego etapu stosowania pali w posadowieniu budowli, wyznaczanie ich nośności było trudnym zadaniem inżynierskim. Testy in-situ (SPT, CPT) szybko wyparły konwencjonalne odwierty połączone z badaniami laboratoryjnymi, ze względu zbyt dużą zawodność klasycznych badań gruntu, np. [1], ale też ze względu na szybkość i niższy koszt testów. Testy penetracyjne: Standardowy Test Penetracji (SPT) i Test Penetracji stożkiem (Cone) (CPT) są szczególnie przydatne do oceny nośności pali, ponieważ opór na wciskanie sondy jest przeliczany bezpośrednio na nośność pala. Projektowanie pali na podstawie sondowań CPT jest obecnie bardzo ułatwione, ponieważ  w podstawowej normie z roku 2009 [2] w załączniku D podano gotową procedurę do wyznaczania nośności pala na podstawie oznaczonego w badaniach CPT, oporu stożka podczas wciskania sondy  $q_c$ oraz tarcia na pobocznicy $f_s$.  W nowej wersji Eurokodu 7 omawiane zagadnienia przeniesiono do części 3 spójnej  z ogólnymi zasadami projektowania konstrukcyjnego.

Metody szacowania nośności pali

Nośność pali można określić pięcioma sposobami:

1. Obciążenia próbne pali w testach  obciążeniowych. Takie testy są drogie i czasochłonne oraz nieprzydatne na etapie projektowania pali,
2. Analiza klasyczna prowadzona z zastosowaniem parametrów gruntu uzyskiwanych z badań laboratoryjnych próbek pobranych z otworów geologicznych. Ze względu na małą dokładność zaleca się potwierdzenie oszacowań w drodze obciążenia próbnego metoda 1,
3. Metody badań in-situ bezpośrednio lub pośrednio w tym na podstawie sondowań SPT (dynamiczne)  lub CPT (statyczne). Metody znacznie dokładniejsze od analizy klasycznej, ale przy bardziej odpowiedzialnych konstrukcjach zaleca się sprawdzenie poprzez obciążenia próbne metodą 1
4. Metody dynamiczne:
   4.1. bazująca na analizie równania falowego,
   4.2. z analizatora wbijania pali (PDA) podczas ruchu palownicy do  osadzania pali wbijanych,
   Metody dynamiczne są obarczone dużą niepewnością szacowania nośności i obecnie są rzadko stosowane. 

Metodom  wyznaczania nośności pala na podstawie sondowania dynamicznego SPT oraz statycznego CPT  poświęcono wiele  prac, a w tym: [3], [4],  [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17],[18], [19].

Analiza klasyczna  i jej niepewności

W metodzie klasycznej  ocenia się odrębnie nośność pobocznicy $F_{shaft}$ i nośność stopy pala $F_{,base}$ i nośność pala $F$ uzyskuje przez proste sumowanie:

$$\begin{equation}  F =F_{base}+F_{shaft}\label{1} \end{equation}$$

Powszechnie stosuje się teorię nośności, w której wykorzystuje się zależności korelacyjne głównie pomiędzy kątem tarcia wewnętrznego gruntu $\Phi$ a współczynnikiem nośności pala $N_q$. Na rys. 1 zestawiono najważniejsze teorie nośności.

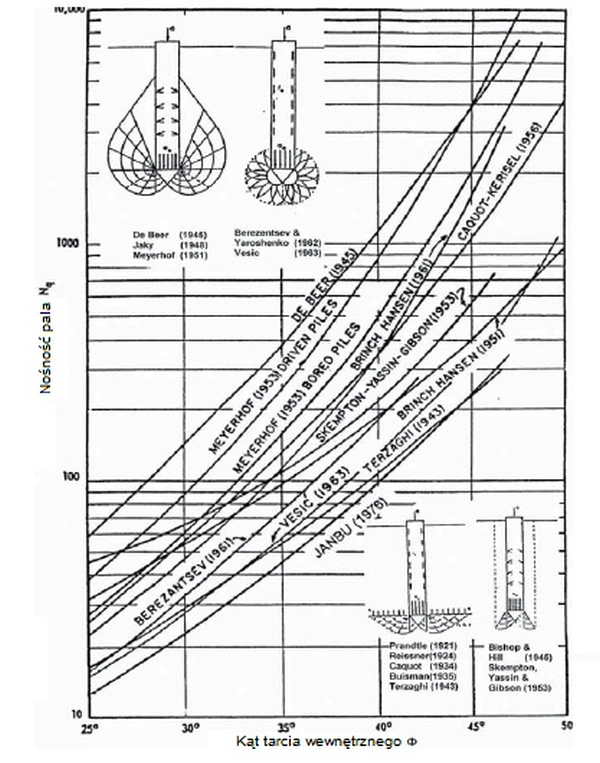
Rys.1. Teorie nośności pala w zależności od kata tarcia wewnętrznego $\Phi$ gruntu na podstawie [20]

Nośność pobocznicy oraz stopy zarówno w gruncie spoistym jak i sypkim wyznaczona jest z wysoką  niepewnością, ponieważ nakłada na się na nią: dokładność oznaczenia parametrów gruntu oraz dokładność teorii korelacyjnej wybranej do wyznaczenia nośności (rys.1).

Współczesne sondowania  CPT i SPT a nośność pala

Szacowanie nośności pala na podstawie wyników testów penetracyjnych gruntu odbywa się na podstawie zależności empirycznych zestawionych w tab.1. [20]), [21].

Historię rozwoju metod szacowania nośności pala na podstawie testów SPT i CPT oraz charakterystyczne cechy metod zaprezentowano w tab.1 . Tabela ta  jest tak skonstruowana, że podaje zależności korelacyjne sprowadzone do liczby uderzeń N sondy SPT. Wyniki CPT przekonwertowano na SPT przy użyciu metody Jefferiesa i Daviesa (1993) [22].

Tab. 1. Szacowanie nośności pala na podstawie sondowania SPT,CPT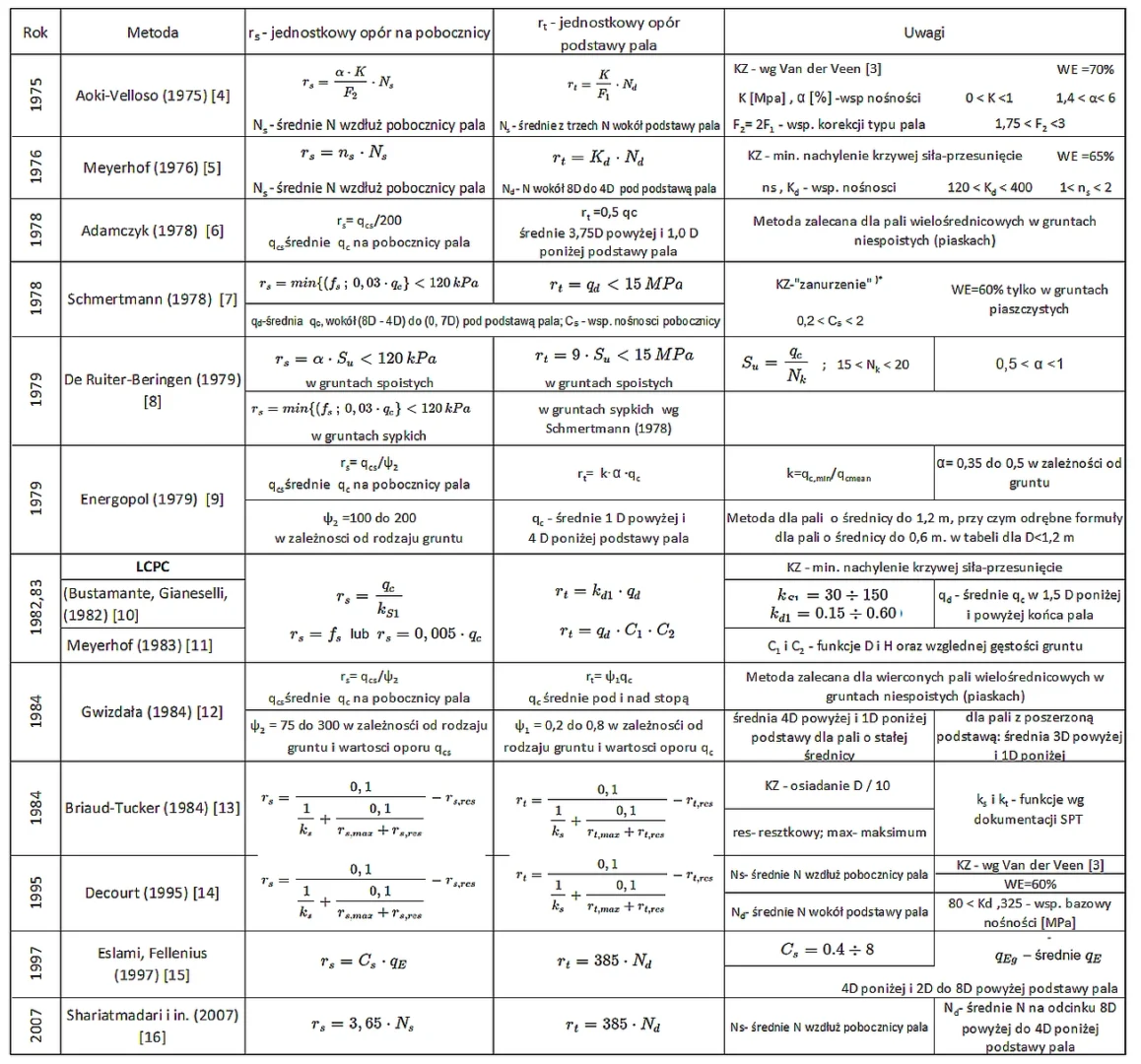W tab.1 zastosowano oznaczenia:
KZ– kryterium zniszczenia. Kryterium zniszczenia KZ nazwana „Zanurzanie” oznacza taki stan, w którym następuje  szybki pionowy ruch pala przy niewielkim wzroście przyłożonego obciążenia. W normie ASTM (American Society for Testing and Materials) i wielu innych jako kryterium „zanurzania” przyjmuje się wzrost osiadania o 10%D,
WE – współczynnik energii
B – średnica pala
H–  głębokość osadzenia pala w nośnej warstwie
f_s –  opór gruntu na pobocznicy tulei sondy,
r_s, r_t ; jednostkowa nośność pobocznicy i podstawy pala odpowiednio. 

Ocena nośności pala wg normy Eurokod 7

Metody zestawione w tab.1  są podstawą sformułowania metody normowej. W dodatku D do nomy [2] podano przykład wyznaczania nośności pojedynczego pala na podstawie wyników badania CPT.

Nośność obliczeniowa pala

Nośność obliczeniową całkowitą pala $R_{c,d}$   wyznacza się z całkowitej nośności charakterystycznej $R_{c,k}$  pala

$$\begin{equation}  R_{c,d} = \cfrac{R_{c,k}}{\gamma_t} \label{2} \end{equation}$$

gdzie częściowy współczynniki bezpieczeństwa:
$\gamma_t=1,1,$ dla pala wciskanego,
$\gamma_t=1,15,$ dla pala wyciąganego ( pobocznicy przy wyciąganiu)

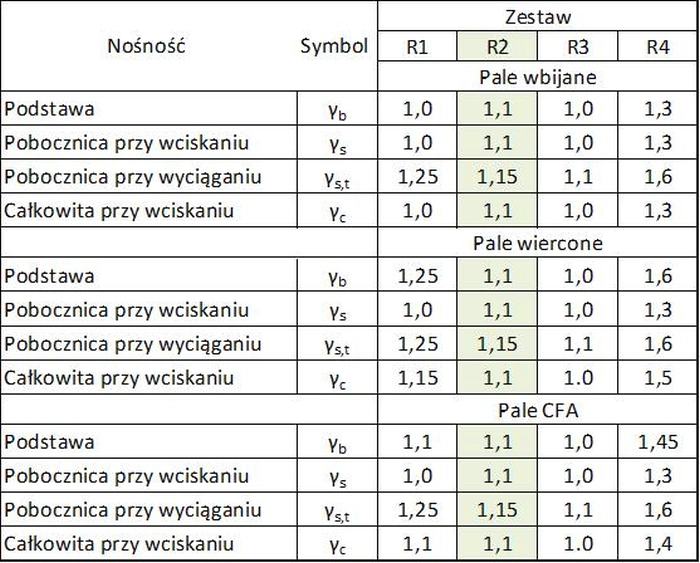
w stosowanym w Polsce zestawie współczynników bezpieczeństwa R2  [23]wg tab.2..

Tab.2  Współczynniki częściowe bezpieczeństwa dla pali w kombinacja geotechnicznych   [23]

Nośność charakterystyczna pala

Całkowitą nośność charakterystyczną pala $R_{c,k}$ wyznacza się na podstawie $n_{CPT}$ punktów pomiarowych  CPT  z zależności

$$\begin{equation}  R_{c,k} = \min{  \left \{ \cfrac{R_{c,mean} }{\xi_3} \quad ; \quad \cfrac{R_{c,min} }{\xi_4} \right \} } \label{3} \end{equation}$$

gdzie:

$R_{c,mean} = \cfrac{1}{n_{CPT}} \sum R_{c,i}$ -w wartość średnia z n_{CPT}  obliczonych nośności całkowitych pala
$R_{c,mean} =  \inf R_{c,i}$ – wartość najmniejsza z n_{CPT}  obliczonych nośności całkowitych pala

Współczynniki korelacyjne $\xi_3$ i $\xi_4$ wyznacza się z tab. 2 na podstawie liczby analizowanych profilów CPT $n=n_{CPT}$

Tab. 3 Współczynniki korelacyjne $\xi$ do wyznaczania wartości charakterystycznych  na podstawie badań podłoża (n – liczba badanych profilów) [23] – tab. A.10

Dla jednego profilu (n=1) $\xi_3=\xi_4= 1,4$.

Szacowanie maksymalnej nośności pala na podstawie badań CPT

 Zgodnie z klauzulą (2) Dodatku D  [2] – maksymalną nośność pala $F_{max}$ można obliczyć z zależności ($\ref{1})$ po podstawieniu maksymalnych składowych:

$$\begin{equation}  F_{max} =F_{max,base}+F_{max,shaft} \label{4} \end{equation}$$

Zależność ($\ref{4}$) została oryginalnie podana dla pali wciskanych, ale jest słuszna dla wszystkich rodzajów pali, w tym najczęściej stosowanych pali  wierconych  CFA. Różnice występują tylko we współczynnikach empirycznych. Rozpatrywane kształty podstaw pala i średnice równoważne trzonu $d_{eq}$ oraz podstawy pala $D_{eq}$ pokazano na rys.2.

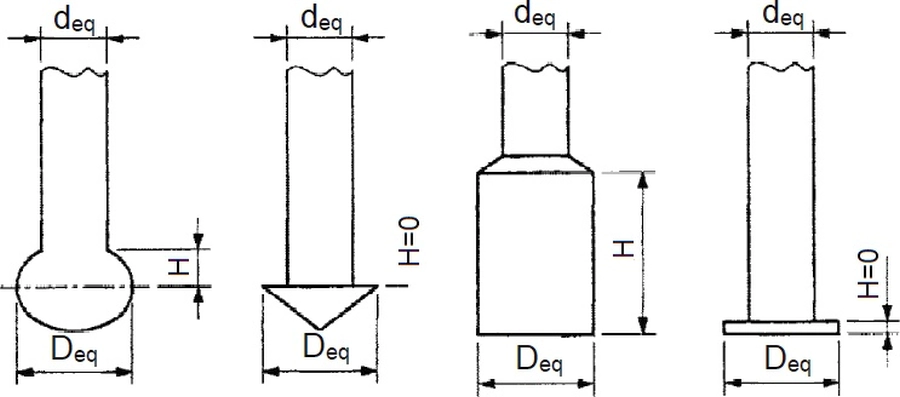
Rys.2 . Średnice równoważne pala wg [2] – rys. D2

W przypadku pala prostokątnego axb  zastępcza średnica pala wynosi

$$\begin{equation} D_{eq}= 1,12 \cdot a \sqrt{\cfrac{b}{a}} \label{5} \end{equation}$$

gdzie:
a- długość krótszego boku pala
b- długość dłuższego boku pala, przy czym b<1,5a.

Definicje oporów stożka do wyznaczania nośności pala

Na rys. 3 zdefiniowano opory stożka  $q_{c,I}$, $q_{c,II}$, $q_{c,II}$ z badania CPT wyznaczane przy szacowania nośności pala. 

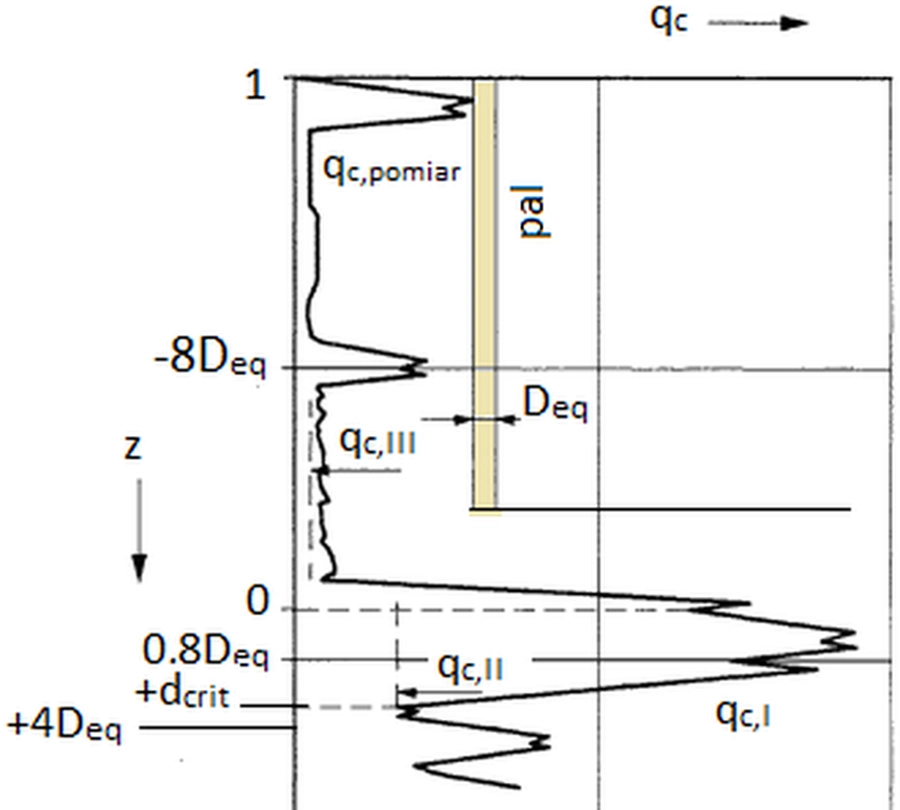
Rys.3  Definicje oporów stożka $q_{c,I}$, $q_{c,II}$, $q_{c,II}$ zmodyfikowany rys. D.2 [24]

Maksymalny opór podstawy pala

Maksymalny opór podstawy pala  $F_{max, base}$ wyznacza się według wzoru

$$\begin{equation} F_{max,base}=A_{base} \cdot p_{max,base} \label{6} \end{equation}$$

gdzie $A_{base}$ – pole powierzchni podstawy pala

Maksymalny jednostkowy opór podstawy pala $p_{max,base}$ wyznacza się na podstawie badań CPT z zależności:

$$\begin{equation} p_{max,base}= 0,5 \cdot \alpha_p \cdot \beta \cdot s \cdot \left( \cfrac {q_{c,I, mean}+q_{c,II,mean}}{2}+ q_{c, III ,mean}\right) \le 15 \, MPa \label{7} \end{equation}$$

gdzie:

• $q_{c,I, mean}$ – średnia z  wartości $q_{c,I}$ w zakresie głębokości od poziomu podstawy pala do poziomu krytycznego $d_{crit}$.

$$\begin{equation}  q_{c,I,mean} =\cfrac{1}{d_{crit}} \int \limits_0^{d_{crit}}  q_{c,I} dz \label{8} \end{equation}$$

Poziom krytyczny $d_{crit}$ to poziom na odcinku ( 0,7 do  4) $D_{eq}$ poniżej podstawy pala, na którym obliczona wartość $p_{max,base}$ ($\ref{7}$) osiąga minimu. W pierwszej iteracji przyjmuje się, ze poziom ten odpowiada minimalnemu oporowi stożka $q_c$ wg rys.3.

Ze sposobu wyznaczania poziomu krytycznego wynika, że badania CPT powinny być przeprowadzone do głębokości min $4 D_{eq}$ poniżej podstawy pala. Ponieważ w  trakcie badań CPT najczęściej nie jest jeszcze znana długość pali, więc przyjmuje się, że zaprojektowana później długość pala nie będzie większa niż głębokość sondowania CPT pomniejszona o $4D_{eq}$. Jeśli taka długość pala okaże się za mała, to należy przeprowadzić dodatkowe sondowania, ale już w ograniczonej liczbie.

• $q_{c,II, mean}$ – średnia z najniższych wartości $q_{c,II}$ w zakresie głębokości mierzonej w górę od głębokości krytycznej do podstawy pala

$$\begin{equation}  q_{c,II,mean} =\cfrac{1}{d_{crit}} \int \limits_{d_{crit}}^0  q_{c,II} dz \label{9} \end{equation}$$

Przy stałym kroku pomiarów – w praktyce stosuje się dyskretną wersję $(\ref {9})$. Najpierw na odcinku krytycznym  typuje się najniższe wartości $q_c$ stanowiące lokalne minima wykresu. Wybrane wyniki przesuwa do zbioru wartości z którego wylicza się średnią arytmetyczną.

$$\begin{equation}  q_{c,II,mean} =\cfrac{1}{N_{inf}}  \sum  \limits_{i=1}^{n_{inf}} q_{c,II,i } \label{10} \end{equation}$$

gdzie: $N_{inf}$ – liczba  najniższych wartości $q_{c,II}$ na odcinku krytycznym

• $q_{c,III, mean}$ – średnia z wartości $q_{c,III}$ w zakresie głębokości mierzonej w górę od poziomu podstawy pala do poziomu, który znajduje się w odległości $8D_{eq}$ powyżej  lub dla podstawy  prostokątnej axb (b<2,5a) do poziomu w odległości $8a$ powyżej podstawy pala. Ta procedura rozpoczyna się od najmniejszej wartości $q_{c,II}$ położonej powyżej poziomu podstawy pala  na odcinku, na którym wyznacza się $q_{c,II,mean}$, a która wystąpiła przed końcowym odcinkiem wzrostu oporu wokół podstawy sondy (pala)

$$\begin{equation}  q_{c,III,mean} =\cfrac{1}{8D_{eq}} \int \limits_0^{- 8D_{eq}} q_{c,III} dz \label{11} \end{equation}$$

Opory stożka $q_{c, I}$, $q_{c, I}$ zdefiniowano na  rys.3.

Współczynnik klasy pala o średnicy $d_{eq}$>150 mm wynosi

$$\begin{equation} \alpha_p= \begin {cases} 1,0 , & \textrm { dla pali przemieszczeniowych } \\ 0,8 , & \textrm { dla pali formowanych świdrem ciągłym} \\ 0,6 , & \text { dla pali wykonywanych w otworze wiertniczym (z płuczką wiertniczą)} \\ \end {cases} \label{12} \end{equation}$$

Klasa  pali przemieszczeniowych obejmuje  pale prefabrykowane zagłębiane w podłożu oraz  wykonywane w podłożu przez zagłębienie rury stalowej z zamkniętym końcem – rura jest usuwana podczas betonowania. Klasa pali formowanych świdrem ciągłym obejmuje najczęściej stosowane obecnie pale CFA.

Współczynnik uwzględniający kształt powiększonej stopy należy z interpolacji pomiędzy granicami podanymi na rys.4  gdzie definicje występujących tam wielkości podano na rys. 2. W przypadku niepowiększonej stopy pala:  β=1,0 

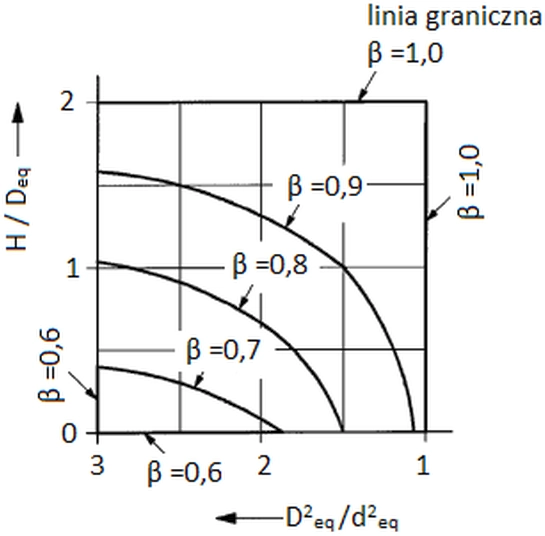
Rys. 4 Współczynnik kształtu powiększonej stopy pala [2] – rys. D4

Współczynnik $s$ uwzględniający kształt prostokątnej podstawy pala LxB (L>B) ; r= L/B; $\varphi’$ oraz efektywny kąt tarcia wewnętrznego, wynosi:

$$\begin{equation}  s= \left ( 1+\cfrac{sin \varphi’}{r}\right)/ (1+sin \varphi’) \label{13} \end{equation}$$

W nowych znowelizowanych normach Eurokod definicję umieszczono w innych miejscach norm ( wprowadzono część 3 Eurokod 7:
$q_{c,I, mean}$ – uśredniony opór gruntu pod stożkiem sondy w strefie podstawy pala $q_{c, I}$   – EN 1997-2, aneksu D7,
$q_{c,II, mean}$ – uśredniony minimalny opór gruntu pod stożkiem sondy w strefie podstawy pala $q_{c, II}$  – EN 1997-3,aneks B4,
$q_{c,III, mean}$ – uśredniony opór gruntu pod stożkiem sondy w strefie podstawy pala $q_{c, III}$  – EN 1997-3, aneks B4

Maksymalny opór pobocznicy pala

Maksymalny opór na pobocznicy pala  $F_{max, shaft}$  wyraża wzór:

$$\begin{equation} F_{max,shaft} = C_p \cdot  \int \limits_0^{ \Delta L} p_{max,shaft,z} dz \label{14} \end{equation}$$

gdzie:
$C_p$ – obwód części trzonu pala, w której umieszczono głowicę pala ,
$p_{max,shaft,z}$ – maksymalne jednostkowe tarcie oddziałujące na pobocznicę na głębokości z – wg badań CPT,
$\Delta L$ – długość pala, na  której aktywowane jest tarcie na pobocznicy lub długość poszerzonej podstawy, przy czym $\Delta L$ nie powinna być większa od: 1) odległości od podstawy pala do spągu pierwszej warstwy  dla  której $q_c < 2 \, MPa$, 2) długości  powiększonej części końca pala, jeżeli zostało zastosowane
$z$ – rzędna wzdłuż osi pala

Maksymalny jednostkowy opór pobocznicy pala  $p_{max, shaft,z}$  na głębokości o rzędnej z wyznacza się z zależności [2] – kl. (4)

$$\begin{equation} p_{max, shaft,z}= \alpha_s \cdot q_{c,z} \label{15} \end{equation}$$

gdzie
$q_{c,z}$ – opór $q_c$ na głębokości z

Współczynnik $\alpha_s$ zależy od klasy pala  i rodzaju gruntów, jak następuje:

$$\begin{equation} \alpha_s= \begin {cases} 0 &\textrm { dla pali w torfach } \\ 0,005 & \textrm { dla pali A w piaskach i pospółce  } \\ 0,006, & \textrm { dla pali B  w piaskach i pospółce } \\ 0,010, & \text { dla pali C  w piaskach i pospółce } \\ 0,012, & \text {dla pali D  w piaskach i pospółce } \\ < 0,020 & \text {dla pali w iłach przy } q_c < 3 \, MPa  \\ < 0,025, & \text {dla pali  w pyłach } \\ < 0,030, & \text {dla pali w iłach przy } q_c > 3 \, MPa \\ \end {cases} \label{16} \end{equation}$$

Pale klasy A i B, to pale wykonywane z usunięciem gruntu o średnicy  > 150 mm, przy czym:
klasa A,  dotyczy  pali wykonywanych  w otworze wiertniczym z płuczką;
klasa B, dotyczy pali formowanych świdrem ciągłym, przy czym  wartość  $\alpha_s =0,006$ jest stosowana  przy wykorzystaniu wyników badania CPTU przeprowadzonego  przed wykonaniem pala . Gdy badanie  CPTU odbyło się w sąsiedztwie pala formowanego świdrem ciągłym, to  $\alpha_s$ można zwiększyć do 0,001;
Pale klasy C i D, to pale przemieszczeniowe  o średnicy  > 150 mm, przy czym:
klasa C, dotyczy pali prefabrykowanych wbijanych;
klasa D, dotyczy pali wykonywanych w podłożu poprzez wbijanie stalowej rury z zamkniętym dnem, rura stalowa jest odzyskiwana podczas betonowania.

Wartości $\alpha_s$ dla pali A,B,C,D są ważne dla piasków od drobno- do gruboziarnistych. W przypadku piasków bardzo gruboziarnistych należy stosować  współczynnik redukcyjny 0,75, a w przypadku żwirów współczynnik redukcyjny wynosi 0,5.

Numeryczny sposób wyznaczania całek  z badania CPT

Całki  występujące w $(\ref{8})$, $(\ref{9})$, $(\ref{11})$ oblicza się numerycznie poprzez zastąpienie sumą, przy czym stosuje się metodę trapezów.  Całkowaną funkcję oporu stożka $q_c$ aproksymujemy liniowo w każdym z podprzedziałów $[  z_{i+1} , z_i ],, \; i=0, \, 1 , \, \dots \, n-1)$. Stały krok całkowania równy odległości pomiędzy rzędnymi pomiarów i wynosi

$\Delta z = \cfrac{z_n -z_0}{n}$,

gdzie n-  liczba przedziałów, $z_0$- rzędna (głębokość) początkowa , $z_n$ – rzędna (głębokość) końcowa

Stosujemy formułę całkowania

$$\begin{equation} \int \limits_{z_0} ^{z_n} q_c (z) dz  \approx  \sum \limits_{i=0}^{n-1} \cfrac{\Delta z }{2} [ q_{c,i+1} +q_{c,i}] = \Delta z \left ( \cfrac{1}{2} q_{c,o} + q_{c,1} +q_{c,2} +\ldots + q_{c,n-1} +\cfrac{1}{2} q_{c,n}\right ) \label{17} \end{equation}$$

gdzie oznaczono   $q_{c,i} =q_c(z_i)$

Analogiczną formułę stosujemy do obliczania całki $(\ref{14})$.

Zastosowanie programu obliczeniowego GEO5

Prowadzenie obliczeń pali na podstawie badań CPT jest znacznie ułatwione  z zastosowaniem arkuszy kalkulacyjnych zestawionych w programie GEO5 [25].

W programie GEO5 zaimplementowano specjalny moduł  Pal CPT służący do do analizy nośności i osiadania pojedynczego pala lub grupy pali z wykorzystaniem wyników sondowań statycznych metodami:

• EN 1997-2
• NEN 6743
• LCPC (Bustamante) (ujęty w tab.1pod poz.5)
• Schmertmann (ujęty w tab.1pod poz.3)

Metodę analizy nośności pali  wybiera się w zakładce „Pale CPT„.

Dla wszystkich tych metod, głównymi parametrami wejściowymi są bezwymiarowe współczynniki służące do oszacowania odpowiednio – nośności podstawy i pobocznicy pala.  W różnych publikacjach spotyka się różne sposoby zapisu tych parametrów. W programie Pale CPT użyto następującego zapisu: $\alpha_p$ –współczynnik redukcji nośności podstawy pala, $\alpha_s$ – współczynnik tarcia na pobocznicy Współczynniki są obliczane automatycznie na podstawie rodzaju pala i otaczającego gruntu – można te parametry również definiować ręcznie ( α_p można definiować w zakładce „Geometria„, natomiast α_s jako parametr charakteryzujący grunt). Przy analizie pali o przekroju prostokątnym, wprowadza się współczynnik kszałtu podstawy pala s (zdefiniowany wyżej) w celu redukcji nośności podstawy. Podczas analizy pali z poszerzoną stopą, wprowadzany jest współczynnik wpływu poszerzenia podstawy pala β , służący do korekcji nośności poszerzonej stopy pala. Podczas obliczania nośności podstawy, program automatycznie uwzględnia wpływ zmiany poziomu terenu.

Program umożliwia obliczenie granicznej krzywej obciążeniowej (obciążenie-osiadanie) i osiadania pala dla danego obciążenia. Do analizy przyjmowane są obliczone wartości nośności podstawy i pobocznicy; analiza wykonywana jest wg normy NEN 6743. Przy obliczaniu osiadania pala można również uwzględnić negatywne tarcie  na pobocznicy.

Użyteczną własnością  programu „Pal CPT” ( równiż „Fundamenty bezpośrednie CPT” i „Stratygrafia 3D”)  jest import wyników badania CPT w różnych formatach, a mianowicie:

• ogólny format tekstowy lub tabelaryczny *.txt, *.xlsx, *.csv, *.ods
• format danych stosowany w Republice Czeskiej i Słowacji, pochodzący z oprogramowania GeProDo *.spe
• standardowe pliki tekstowe w formacie  *.CPT z kilku programów:
  > Geodelft M-Serie (stosowane powszechnie w Holandii) ,
  > Geotech AB CPT,
  > Gouda Geo CPT,
  > Hogentogler CPT
• ogólny język  przechowywania i przekazywania danych geotechnicznych. *.GEF GEF (Geotechnical Exchange Format)  (więcej informacji na ten temat można znaleźć w: https://publicwiki.deltares.nl/display/STREAM/GEF-CPT )
• format wykorzystywany do transferu danych geotechnicznych w Wielkiej Brytanii *.AGS ,  (więcej informacji na ten temat można znaleźć w: ttp://www.agsdataformat.com/datatransferv4/intro.php)
• format danych stosowany w Polsce *.GRU

Oczywiście można też dane wprowadzać ręcznie, ale zaleca się zamawiać  badania wraz z dostarczeniem pliku  z wynikami pomiarów w jednym  z wyżej wymienionych formatów.

Przykłady rachunkowe

Przykład 1 [sprawdzenie nośności pala na podstawie CPT]

Sprawdzić nośność pala obciążonego osiowo siła obliczeniową $V_d=$ 3800 kN
Pal wiercony, wykonano   w rurze osłonowej wyciąganej: o średnicy  D= 800 mm , o długości L= 13 m w gruncie z charakterystyką z badań CPT pokazaną na rys. 5.

Wyniki badań CPT zaczerpnięto z pracy Puła (2013) [26].

Parametry geometrii pala

Dla pala wierconego w rurze osłonowej o przekroju kołowym:

$D_{eq}=d_{eq} =D = 0,8 \, m$

$(\ref{5})  \to A_{base} = \pi \cdot D^2/4= \pi \cdot 0,8^2/4 = 0,503 \, m^2$

$(\ref{6})  \to  C_{shaft} = \pi \cdot D_{eq} = \pi \cdot 0,8 = 2,5  \, m$

Wykres z oznaczenia sondą CPT

Oryginalny wykres z oznaczenia CPT zaprezentowano na rys.5  wg pracy Puła (2913) [26].

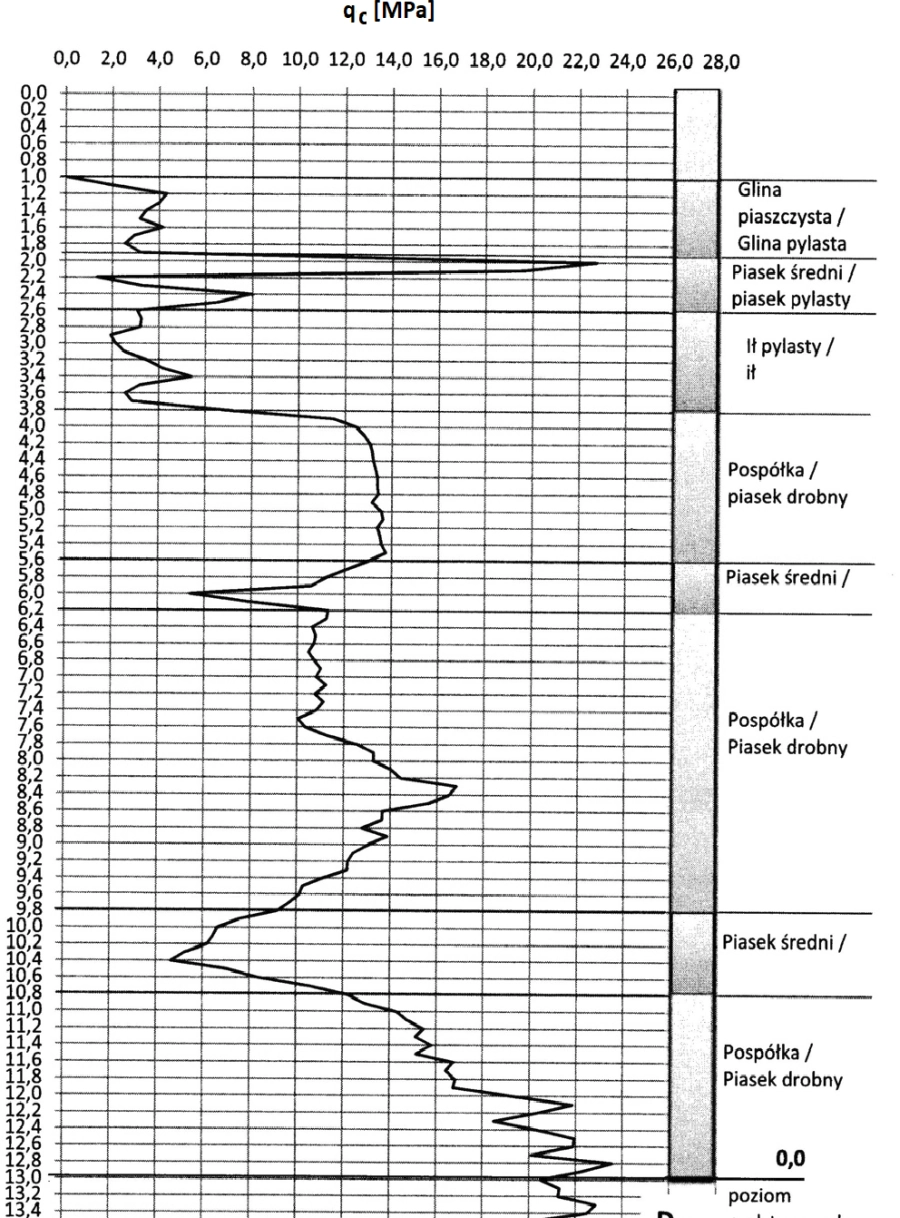
Rys.5. Wykres z badań CPT [26]

Badania rozszerzone pod stopą pala

W celu wyznaczenia potrzebnych parametrów wymagane są rozszerzone badania CPT na głębokości $4D_{eq}$ pod stopą pala. Takie badania zapisano do pliku tekstowego i przedstawiono w  tabeli liczbowej w tab.5 .

Tab.3  Tabela liczbowa (badania CPT z przykładu 1 oraz wyznaczenie parametrów $q_{c, mean}$ i $p_{c,shaft}$
[kliknij, aby pobrać w formacie *.ods ]

Poziom krytyczny

Rozpatrujemy  odcinek wykresu pomiędzy poziomami:

poziom górny $z_T =0,7 D_{eq}= 0,7 \cdot 0,8= 0,56 \, m \to h_T= 13,0+0,56=13,56 \,m$
poziom dolny $z_D =4 D_{eq}= 4 \cdot 0,8= 3,2 \, m \to h_D=13,0+3,2=16,2 \,m$

Na  długości tego odcinka krytycznego  minimalną wartość oporu stożka $q_c$ zaobserwowano na poziomie $z_{crit}= 16,00\, m$ o wartości  $q_c= 16,418 \, MPa$

Stąd długość  krytyczna $d_{crit} =16,00-13,00 =3,00 \, m$

Powyższe obserwacje zaznaczono W tabeli liczbowej z badań CPT (tab.2) oraz pokazano na rys. rys.6.

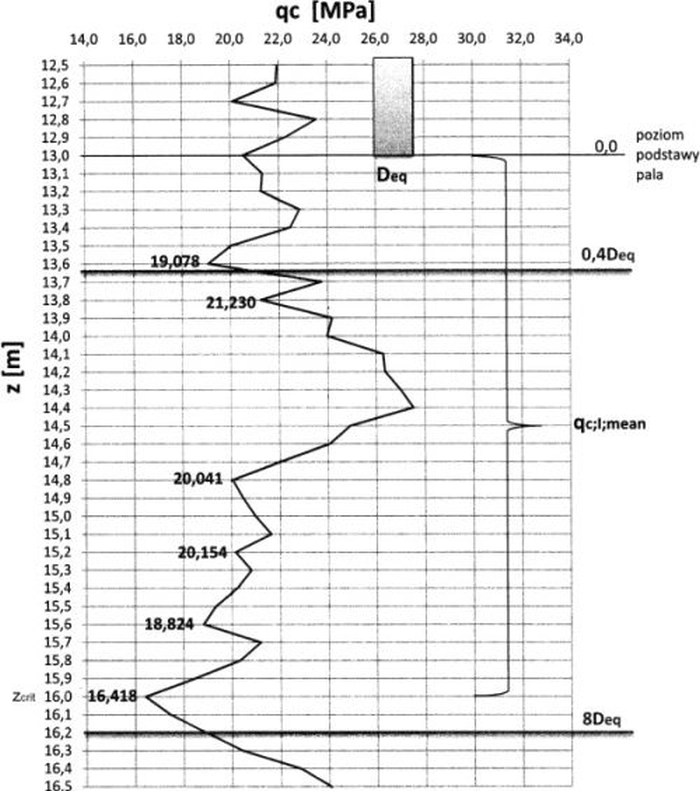
Rys.6. Wyznaczenie wartości $d_{crit} [26]

Uśredniony opór stożka  wokół podstawy pala

Na długości krytycznej $d_{crit}$ od poziomu $z_0=13,00 \,m$ do poziomu $z_{30}=16,00 \,m$ dokonano N=31 pomiarów , to znaczy  liczba przedziałów (kroków) pomiaru wynosiła

$n=N-1 = 30-1=30$

Krok pomiaru wynosił

$\Delta z = \cfrac{d_{crit}} {n} = \cfrac{ 3,00}{30}= 0,10 \, m$

Uśredniony opór stożka $q_{c,I,mean}$ wyznacza się na odcinku  $(0 \, ; \, d_{crit})$ , który oznaczono klamrą na rys.6.

Korzystając z zależności $(\ref{8})$ aproksymowanej  $(\ref{17})$ otrzymujemy

$q_{c,I,mean} =\cfrac{1}{3,0 } \cdot (0,1 \cdot (21,26/2+ 21,20 + \ldots +18,4 + 16,42/2 ) = 22,74  \, MPa$

Średni opór  najniższych  wartości

W tab. 2 wybrano najmniejsze wartości oporu stożka na odcinku krytycznym. Korzystając z dyskretnej wersji  $(\ref{10})$  dla $N_{inf}=6$  otrzymano:

$q_{c,II,mean} = \cfrac{1}{8} \cdot  (16,42+ 18,82 + 20,15+20,04+21,23 +19,08) = 19,29 \, MPa$

Uśredniony opór  powyżej podstawy pala

Rozpatrujemy  odcinek wykresu pomiędzy poziomami:

poziom górny $z_T =- 8 D_{eq}= -8 \cdot 0,8= – 6,4 \, m \to h_T= 13,0- 6,4=6,6 \,m$
poziom dolny $z_D = inf q_{c,II}= -1,14 \, m$ wyznaczony jako najmniejsza wartość $q_{c,II}$ poza obszarem wzmocnienia wokół podstawy pala \to h_T= 13,0- 1,14 =11,8 \,m $

Fragment wykresu $q_c$ sondowań sondą CPT potrzebny do wyznaczenia  parametru $q_{c,III,mean}$ pokazano na rys. 7.

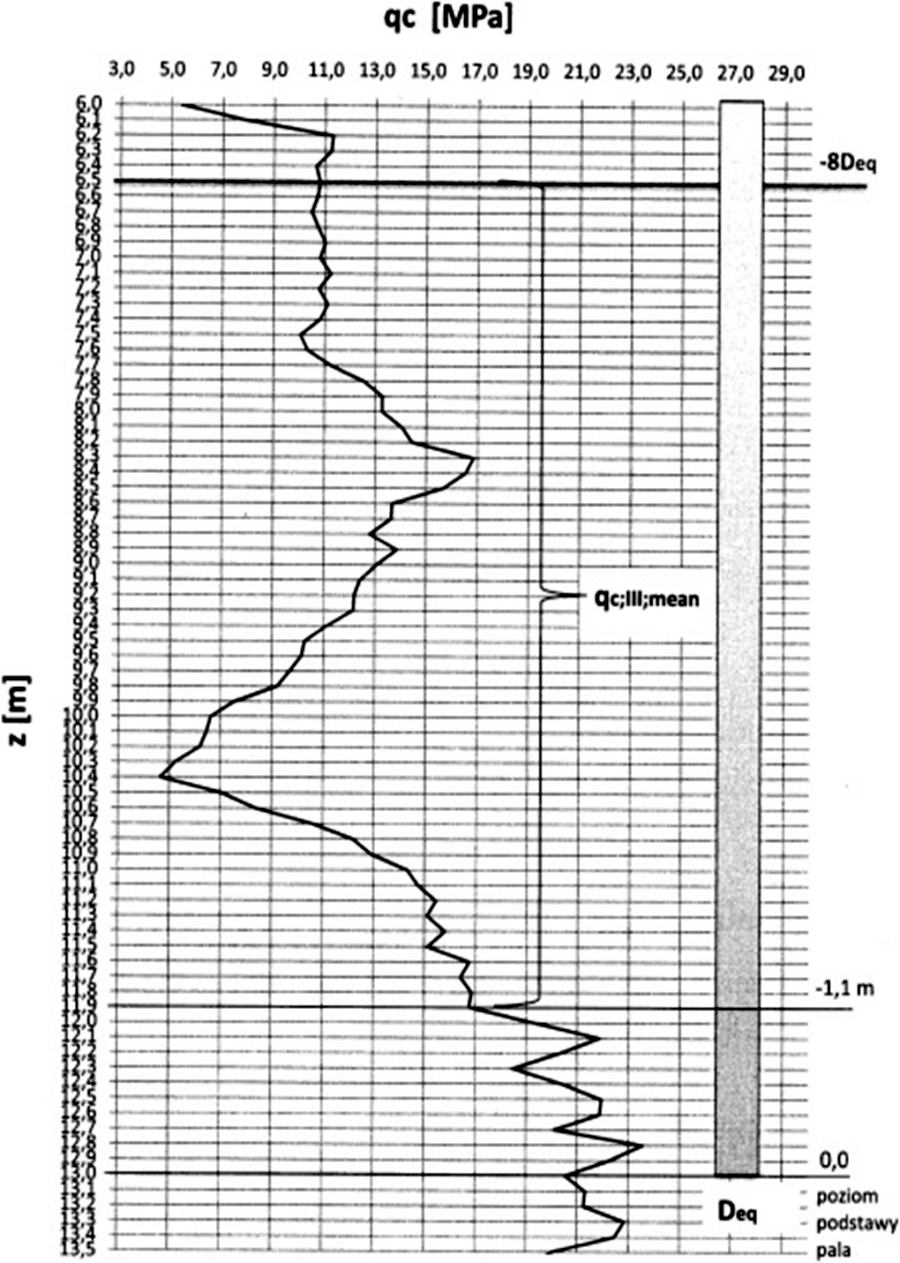
Rys.7 Fragment wykresu CPT do wyznaczania $q_{c,III,mean}$ [26]

($\ref{11}$) $\to$ $q_{c, III , mean} = \cfrac{1}{6,4} \cdot 0,2 \cdot\cdot ( 10,56/2+ 10,54 + \ldots + 16,40 +16,70/2) = 9,70 \, MPa$

Maksymalny jednostkowy opór podstawy pala

$(\ref{12})$ $\to$ $\alpha_p =0,6$
rys.4 $\to$ $\beta =1,0$ ( stopa nie powiększona)
$(\ref{13})$ $\to$ $s =1,0$ (pal nie prostokątny)
$(\ref{7})$ $\to$  $p_{max,base} =  0,5 \cdot 0,6 \cdot 1,0 \cdot 1,0 \cdot \left( \cfrac{22,74+ 19,29}{2}+9,70 \right)= 9,21 \le 15 \, MPa$

Maksymalny jednostkowy opór tarcia gruntu na pobocznicy

Opór tarcia pobocznicy wyznaczony ze wzoru $(\ref{15})$ , zestawiono  w ostatniej kolumnie tab.2. Współczynnik tarcia $\alpha_s$ $(\ref{16})$ podano w przedostatniej kolumnie rys. 7.  W tabeli obliczono też  czynnik pod całką siły tarcia $(\ref{14}$), korzystając z formuły całkowania numerycznego $(\ref{17})$

Długość pala, na  której aktywowane jest tarcie na pobocznicy przyjęto jako całkowitą długość pala
$\Delta L= 13 \, m$.
Tak przyjęta $\Delta L$  nie jest  większa od odległości od podstawy pala do spągu pierwszej warstwy  dla  której $q_c < 2 \, MPa$,, ponieważ dla każdej warstwy $q_c \le  2 \, MPa$. Nie zostało też zastosowane powiększenie części końca.

Otrzymano

$\int \limits_0^{ \Delta L} p_{max,shaft,z} dz = 0,66 \, MN/m$

Obliczone tarcie pobocznicy

$(\ref {14})$ $\to$ $F_{max,shaft} = 2,51 \cdot 0,66 =1,66 \, MN$

Obliczony opór podstawy

$(\ref{6})$ $\to$ $F_{max,base} = 0,503 \cdot 9,21 = 4,63 \, MN$

Obliczona całkowita nośność pala

$(\ref{4})$ $\to$ $F_{max} = 4,63 + 1,66 = 6,29 \, MN$

Nośność charakterystyczna pala

$(\ref{3})$ $\to$ $R_{k,c} =\cfrac{F_{max} }{\xi_3}= \cfrac{6,29}{1,4} =4,49 \, MN$

Nośność obliczeniowa pala

$(\ref{2})$ $\to$ $R_{d,c} =\cfrac{4,49}{1,1} =4,08 \, MN$

Sprawdzenie nośności pala

$V_d=3800 \, kN \le R_{d,c} =4008 \, kN$
OK.Literatura

1. Lunne, T., Robertson, P.K. , Powell, J.J.M. (1997), Cone penetration test in geotechnical practice. Blackie Academic & Professional
2. PN-EN 1997-2:2009, Projektowanie geotechniczne, Część 2: Rozpoznanie podłoża gruntowego
3. Van der Veen, C., (1953), The bearing capacity of a pile. In: Proceeding  International Conference on Soil Mechanics and Foundation Engineering, 3. Zurich. , v. 2, p. 84-90
4. Aoki, N.,  Velloso, D.A. (1975),  An approximate method to estimate the bearing capacity of piles. Proceeding of the Fifth Pan-American Conference on Soil Mechanics and Foundation  Engineering, Buenos Aires, Argentina, pp. 367–376
5. Meyerhof, G.G. (1976),  Bearing capacity and settlement of pile foundations. The Eleventh Terzaghi Lecture, American Society of Civil Engineers, ASCE, Journal of Geotechnical Engineering, Vol. 102, GT3, pp. 195–228
6. Adamczyk J., (1978) ,Określenie udźwigu pali wierconych za pomoca sondy statycznej , Inżynieria i Budownictwo , nr. 7
7. Schmertmann, J.H. (1978), Guidelines for cone test, performance and design. Federal Highway Administration, Report FHWA-TS-78209, Washington, 145 p.
8. DeRuiter J. , Beringen, F.L. (1979),  Pile foundation forlarge North Sea structures. Marine Geotechnology,Vol. 3, No. 3 pp. 267–314
9. Energopol, (1979), Instrukcja  przewidywania nośności pali w oparciu o badania presjometryczne i sondoeania statyczne, COBR, Budownictwa Hydrotechnicznego, Energopol, Warszawa
10. Bustamante, M. , Gianeselli, L. (1982), Pile bearing capacity predictions by means of static penetrometer CPT. Proceedings of the Second European Symposium on Penetration Testing ESOPT-2, Amsterdam, May 24–27, A.A. Balkema, Vol. 2, pp 493–500.
11. Meyerhof, G.G. (1983), Scale effects of ultimate pile capacity, American Society of Civil Engineers, ASCE, Journal of Geotechnical Engineering, Vol. 108, No. GT3, pp. 195–228.
12. Gwizdała K., (1984), Large diameter bored piles in non-cohesive solis . Determination of the bearing capacity  and settlement  from results of static penetration test (CPT) and standard penetration test (SPT), Swedish Getechnical Institute, Report No 26
13. Briaud, J.L., Tucker L.M. (1984),  Piles in sands: a method including residual stresses. ASCE, Journal of Geotechnical Engineering, Vol 110, No. 11, 1666–1680
14. Decourt, L. (1995), Prediction of load-settlement relationships for foundations on the basis of the SPT-T. Ciclo de Conferencias Internationale, Leonardo Zeevaert, UNAM, Mexico, pp. 85–104.
15. Eslami, A.,  Fellenius, B.H. (1997). Pile capacity by  direct CPT and CPTu methods applied to 102 case histories, Canadian Geotechnical Journal, Vol. 34, pp. 886–904
16. Shariatmadari, N., Eslami, A.,  Karimpour-Fard, M. , (2008), Bearing capacity of driven piles in sands from SPT- applied to 60 case histories,  Iranian Journal of Science and Technology, v. 17, p. 35–58
17. Gwizdała K., (2010), Fundamenty palowe. Technologie i obliczenia, tom.1, PWN, Warszawa
18. Czado B.(2014),  Analiza nośności pali fundamentowych na podstawie polowych badań gruntów metodą statyczną, Praca doktorska, Politechnika Krakowska, Wydział Inżynierii Lądowej, Instytut Mechaniki Budowli, Zakład Współdziałania Budowli z Podłożem
19. Saftner D., Dagger R.,  Mayne P., (2018), Cone Penetration Test Design Guide for State Geotechnical Engineers, Report 2018-32, Department of Civil Engineering University of Minnesota Duluth, [http://mndot.gov/research/reports/2018/201832.pdf ]
20. Karimpour-Fard M., Eslami A. (2013), Estimation of vertical bearing capacity of piles using the results CPT and SPT tests, Geotechnical and Geophysical Site Characterization 4 – Coutinho & Mayne (Eds
21. Bandini, P., Salgado, R. (1998),  Methods of pile design based on CPT and SPT results. Geotechnical site characterization conference, Blekma, Rotterdam,pp. 936–942
22. Jefferies, M.G. & Davies. M.P. 1993. Use of CPTU to estimate equivalent SPT N60. Geotechnical Testing Journal, Vol.16, No. 4, pp. 458–468.
23. PN-EN-1997-1, Projektowanie geotechniczne. Część 1. Zasady ogólne
24. Projektowanie geotechniczne, Część 2: Rozpoznanie podłoża gruntowego
25. GEO5 Oprogramowanie geotechniczne, https://www.finesoftware.pl/oprogramowanie-geotechniczne/
26. Puła O., Fundamenty palowe według Eurokod 7, Dolnośląskie Wydawnictwo Edukacyjne, Wrocław, 2013

________________________________