W konstrukcjach budowlanych często należy zapewnić punktowe przekazywanie obciążeń (rys 1a) lub swobodny przesuw (rys. 1b,c) lub wzajemny obrót (też rys.1 a) elementów konstrukcyjnych. Do tych celów służą łożyska konstrukcyjne. Dawniej stosowane, ale już przestarzałe łożyska pokazano na rys.1, na rys. 2 przedstawiono proste nowoczesne łożysko elastomerowe. Ewolucję lóżysk mostowych przed erą łożysk elastomerowych przedstawiono na rys. 3.
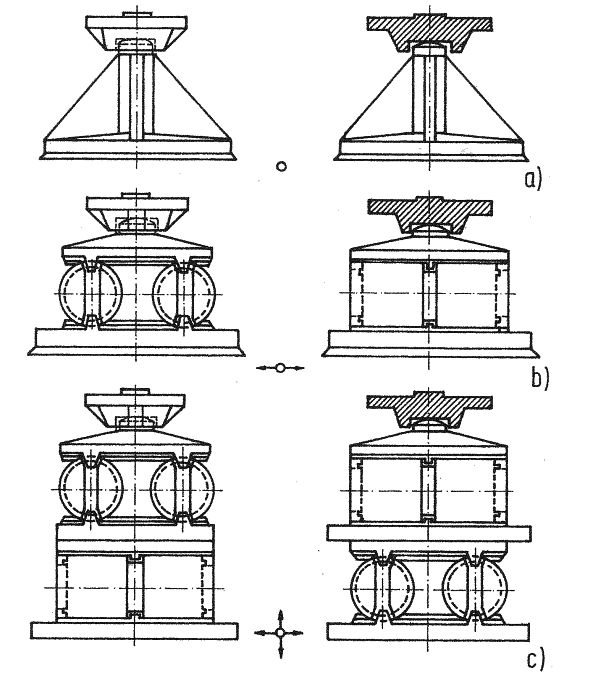
Rys.1 Tradycyjne, przestarzałe już łożyska w konstrukcjach budowlanych [1], str. 1123
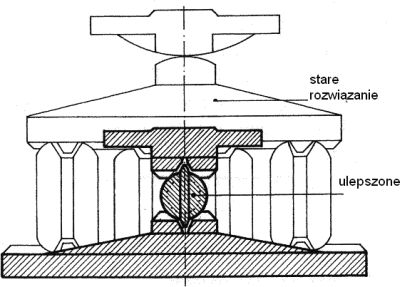
Rys. 3 Ewolucja tradycyjnych łożysk mostowych [1], str. 1124
Przegląd łożysk konstrukcyjnych
Na rys. 4 zestawiono najważniejsze typy łożysk stosowane w konstrukcjach, najczęściej w mostach
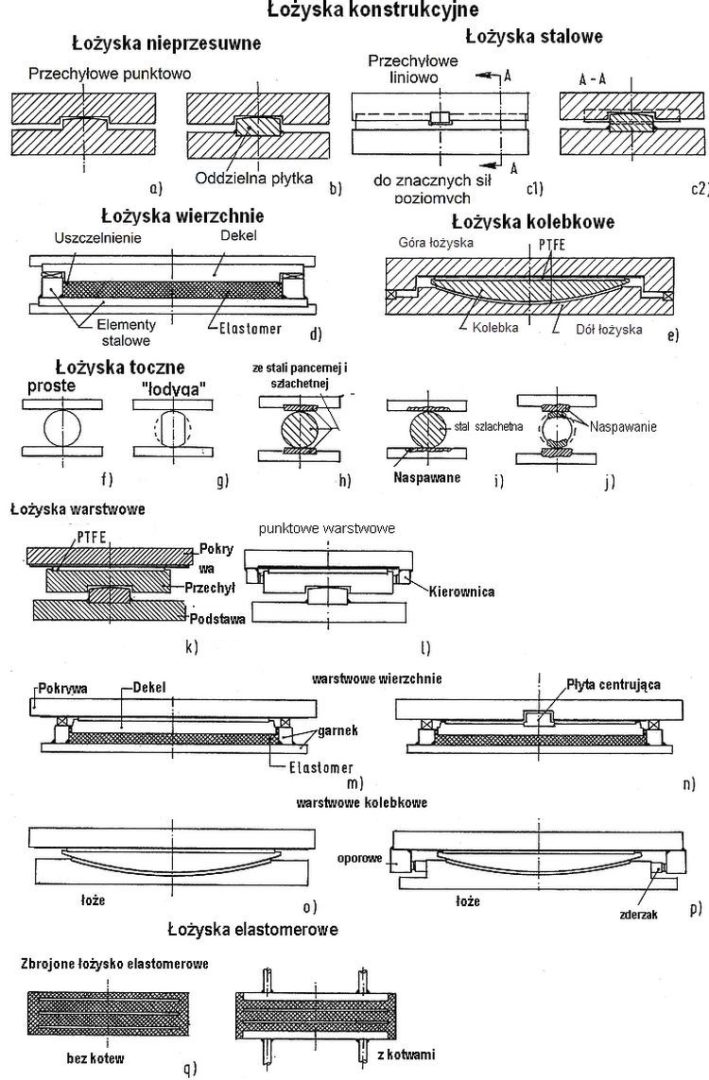
przeglad-lozyskRys. 4 Przegląd łożysk konstrukcyjnych [1], str. 1127
Zagadnienie Hertza
W przypadku łożysk ważnym zagadnieniem jest zadanie wyznaczenia naprężeń w miejscu styku dwóch dociskanych do siebie ciał. Zagadnienie stykowe lub kontaktowe rozwiązał już w 1881 roku w pracy [2].
Siła docisku jest przenoszona z jednego ciała na drugie na bardzo małej powierzchni, jaka tworzy się w wyniku miejscowych odkształceń wywołanych naciskami (rys. 5).
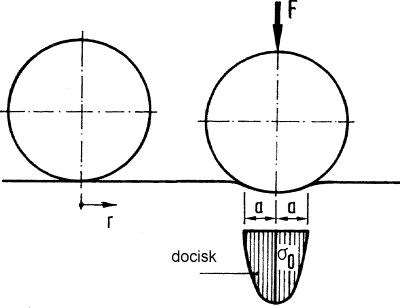
Rys. 5 długość stykających się ciał 2a [1], str. 1128
Zagadnienie rozkładu naprężeń w miejscach styku dociskanych ciał opiera się na założeniach ( Hertza): a) materiał stykających się ciał jest izotropowy i spełnia prawo Hooke’a, b) przy dociskaniu ciał występują tylko naprężenia normalne, c) powierzchnia styku jest ciągła oraz mała w stosunku do wymiarów ciał stykających się.
Wzory Hertza dla jednego z najprostszych (i najczęstszych) przypadków, ściskania wzajemnego dwóch kul, określają promienie powierzchni zetknięcia się kul $r_1$ oraz $r_2$, a także stałe materiału kul : moduły Younga $E_1$ , $E_2$ oraz współczynniki Poissona $\mu_1$, $\mu_2$. Zależnie od konfiguracji kul wyznaczamy promień zastępczy $ r_0 $:
| $\dfrac {1}{r_0}=\dfrac{1}{r_1}+\dfrac{1}{r_2}$, | (1) |
gdzie: $r_2>0$ dla kuli wypukłej, $r_2= \infty$ dla powierzchni płaskiej oraz $r_2<0$ dla kuli wklęsłej (rys. 6)
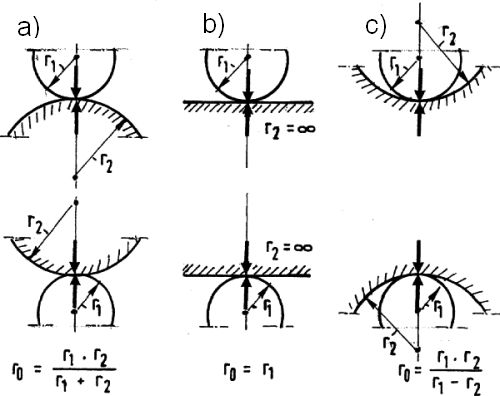
Rys.6. Przypadki kontaktu dwóch kul [1],1128
Zastępczy moduł Younga $E_0$ wyznacza się ze wzoru:
| $ \dfrac {1}{E_0}=\dfrac{1 -\mu_1^2}{E_1}+\dfrac{1-\mu_2^2}{E_2}$ | (2) |
W przypadku kontaktu kula/kula stosujemy następujące formuły:
| $ a=\sqrt[3]{\dfrac{3F r_0}{4E_0}}$, $\sigma_0=\dfrac{3F}{2\pi a^2}$, | (3) |
a w przypadku kontaktu walec/walec o długości $b$ stosujemy formuły:
| $ a=2\sqrt{\dfrac{F r_0}{\pi E_0 b}}$, $\sigma_0=\dfrac{2F}{2\pi a b}$, | (4) |
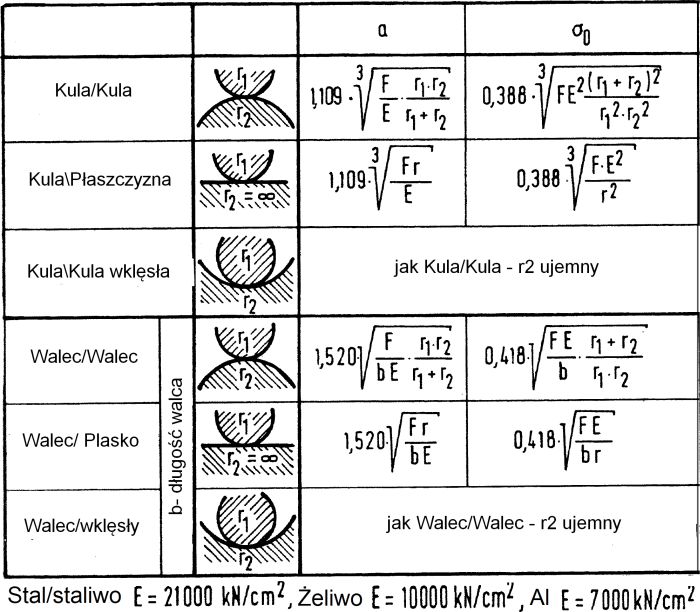
W przypadku współczynnika Poissona $\mu=0,3$ (dla metalu) $a$ oraz $\sigma_0$ można obliczyć z zależności zamieszczonych w tab.1
Tab.1 Wzory Hertza dla metalu [1],1129
Łożyska z materiałem elastycznym
Dawniej łożyska konstruowano z punktowym lub liniowym stykiem (rys.7a,b). Współcześnie stosuje się styk powierzchniowy z zastosowaniem elastycznego materiału (rys. 7 b,c). (p. też łożuska elastomerowe).
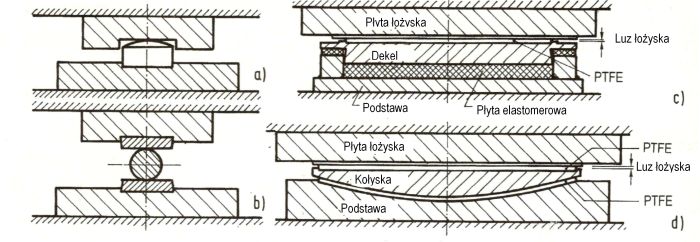
Rys.7 Łożyska: a,b) tradycyjne z punktowum stykiem, b,c) współczesne z materiałem elastycznym [1],1146
Modele pracy łożyska z elastycznym materiałem pokazano na rys.8. PTFE , to inaczej teflon.
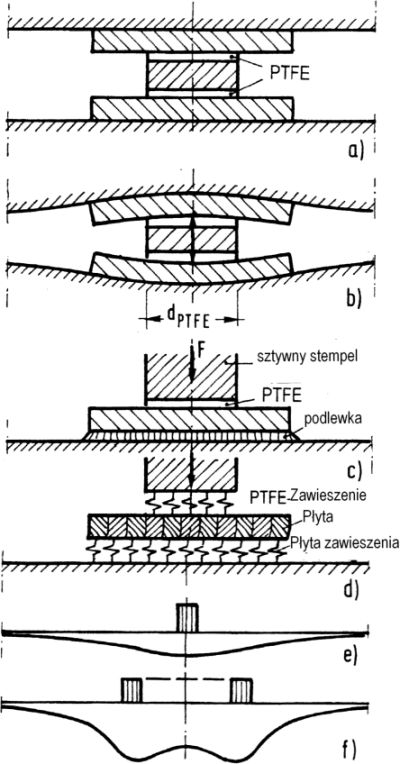
Rys.8 Modele pracy łożyska z elstycznym materiałem : a,b) stempel z przekładkami z teflonu (PTFE) przed i po odkształceniu, c) stempel zawieszony na materiale elastycznym, b) praca stempla c) model stempla , e), f) dwa charakterytyczne rozkłady naprężeń [1], str. 1146
- Petersen C. (2013), Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
- Hertz, H. (1881), Uber die Beruhrung fester elastischer Korper. J. Fur Reine Und Angewandte Mathematik, 92, 156–171
________________________________





