Kopuła siatkowa (inaczej kopuła prętowa) jest efektownym przekryciem dwukrzywiznowym, aproksymowanym siatką prętów. Taka kopuła składa się z węzłów oraz „reszty kopuły”. Najczęściej wykonana jest  ze stali, a jej rozpiętość dochodzi do kilkuset metrów. Po opatentowaniu  w roku 1947 przez Fullera sposobów podziału sfery na trójkąty sferyczne – kopuły siatkowe w typie geodezyjnym, prawie zupełnie wyparły stosowanie innych typów kopuł, a w szczególności zwartych kopuł powierzchniowych, w tym żebrowych, ale współcześnie największe rozpiętości kopuł siatkowych uzyskuje się dla innego niż geodezyjny układu siatki.

 Na rys. 1 pokazano jedną z najbardziej znanych i złożonych kopuł siatkowych – przekrycie  obiektu „Złote Tarasy” w Warszawie.

Rys.1a. Przekrycie „Złote Tarasy” – jedna z najbardziej efektownych realizacji kopuł siatkowych. Widok z zewnątrz obiektu (foto własne)

Rys.1b. Przekrycie „Złote Tarasy”. Widok z wewnątrz obiektu (foto własne)

Wprowadzenie

Definicja kopuł siatkowych. Powierzchnie bazowe, a siatka prętów

Przyjmiemy definicję, ze kopuła siatkowa jest to dowolna siatka spójnych linii, ułożonych na dowolnie zakrzywionej powierzchni klasy przynajmniej C¹ (tzn gładkiej i spójnej). Nieograniczona jest różnorodność zarówno rodzajów zakrzywionych, bazowych powierzchni, jak i rodzajów siatek linii (krawędzi, prętów), tym bardziej, że powierzchnie można składać poprzez klejenie kopuł prostych, czego wynikiem może być powierzchnia z rys.1. Nazwa „siatkowe” (przekrycia (w tym kopuły), pochodzi od siatki prętów oplatających aproksymowaną powierzchnię.
Stosujemy rozszerzoną- nowoczesną definicję kopuł siatkowych w stosunku do definicji historycznej [1], [2] zgodnie z którą miały to być przestrzenne konstrukcje  prętowe powstałe przez przekręcenia pasa dolnego w stosunku do węzłów górnych i koniecznie o nieparzystej liczbie boków podstawy (dla parzystej otrzymywano kopułę chwiejną).

Geometria powierzchni bazowych ma decydujące wpływ na niemal wszystkich cechy struktury: jej nośność i sztywność, technologiczność (prostotę wykonania), a także estetykę, czyli generalnie na jakość  konstrukcji i architektury.

Optymalne powierzchnie  zakrzywione wykształciła sama natura. Są wśród nich krople wody – sfery lub napięte błony ułożone na powierzchni, pancerze żółwi i pancerników, muszle morskie,  spiralne muszle ślimaków [3] lub liście i kwiaty roślin [4].  Z bogactwa kształtów powierzchni natury oraz z wszechobecnego w naturze, złotego podziału – od wieków czerpie architektura: nurt historyczny architektury organicznej- modernizm organiczny, ale przede wszystkim  nurty współczesne: biomitektura, architektura bioekstensywna i blobitektura [5].

W każdym przypadku kształtowania powłok siatkowych należy rozpocząć od poprawnego, matematycznego  zdefiniowania powierzchni na której powłoka ma być rozpięta. Powierzchnie naturalne najczęściej da się opisać prostymi wyrażeniami matematycznymi. Postać funkcji bazowych najlepiej dobrać na podstawie doświadczenia, tak by w konfiguracji zadanych ograniczeń geometrycznych i dla dominujących obciążeń, zachowywała dobrą sztywność i stateczność (mała wrażliwość na lokalne przeskoki – przenicowanie). Na przykład  sfera kulista jest optymalna do przejęcia równomiernego ciśnienia ; sfera paraboloidalna do obciążeń grawitacyjnych. Kształt optymalny powierzchni bazowej odpowiada stanowi błonowemu , to znaczy takiemu, w którym w powłoce wstępują wyłącznie siły rozciągające bez udziału zginania i z niewielkim udziale ściskania.  Często w celu doboru kształtu powierzchni prostych przeprowadza się doświadczenia lub symulacje numeryczne poprzez badanie zachowania łańcucha (liny sznurka), lub gumowej membrany, lub bańki mydlanej. Jeśli w podobnych warunkach brzegowych (kształcie brzegu, podporach i obciążeniu) łańcuch lub membrana układa się w określony kształt, to jest to właśnie kształt optymalny i stosownie do tego dobiera się bazowe powierzchnie aproksymacyjne. Zestawienie najczęściej stosowanych bazowych powierzchni aproksymacyjnych podano w  tab.1.

Prawidłowy dobór powierzchni bazowych (prostych) jest warunkiem koniecznym do tego , by  można było zastosować powłokę prętową w jednej warstwie. W przypadku znaczącego zginania, w tym zaburzeń brzegowych należy stosować sztywne dźwigary brzegowe lub siatkę dwuwarstwowową.  Pomimo tego,że powierzchnie zakrzywione na których rozpięte są siatki jedno- lub dwu-warstwowe są takie same, to analiza konstrukcyjna i detale połączeń są zupełnie inne. Jednowarstwową powłokę konstruuje się zwykle ze sztywnymi węzłami, a w dwuwarstwowej powłoce stosuje się przegubowe połączenia węzłów. Połączenia sztywne prętów powłoki jednowarstwowej zapobiegają przeskokowi węzłów i drastycznie zwiększają sztywność powłoki, co jest szczególnie ważnie w przypadku obciążeń dynamicznych, np obciążenia wiatrem. W przypadku wystarczającego zbadania zjawiska przeskoku (stateczności globalnej ) częstotliwości drgań własnych oraz odporności na skręcanie powłoki siatkowej – można zastosować przegubowe połączenia prętów również w powłoce jednowarstwowej. 

Generalnie, rozpięta na powłoce siatka linii (prętów, krawędzi)  powinna zapewnić geometryczną niezmienność systemu, charakteryzować się małą wrażliwością na przeskok węzłów, a także posiadać optymalne własności technologiczno-ekonomiczne: składać się z jak najmniejszej liczby różnych elementów (prętów i węzłów) i zużywać mało materiału (stali, drewna lub  betonu).

Podstawowe, bazowe powierzchnie aproksymacyjne

Podstawowe powierzchnie bazowe na których można rozpiąć siatkę prętów, zestawiono w tab.1.

Tab.1. Podstawowe powierzchnie bazowe sklepień i kopuł  (oprac. własne)  

Nazwa	Rysunek	Formuła	Uwagi
Powierzchnie II stopnia (kwadryki)
Elipsoida		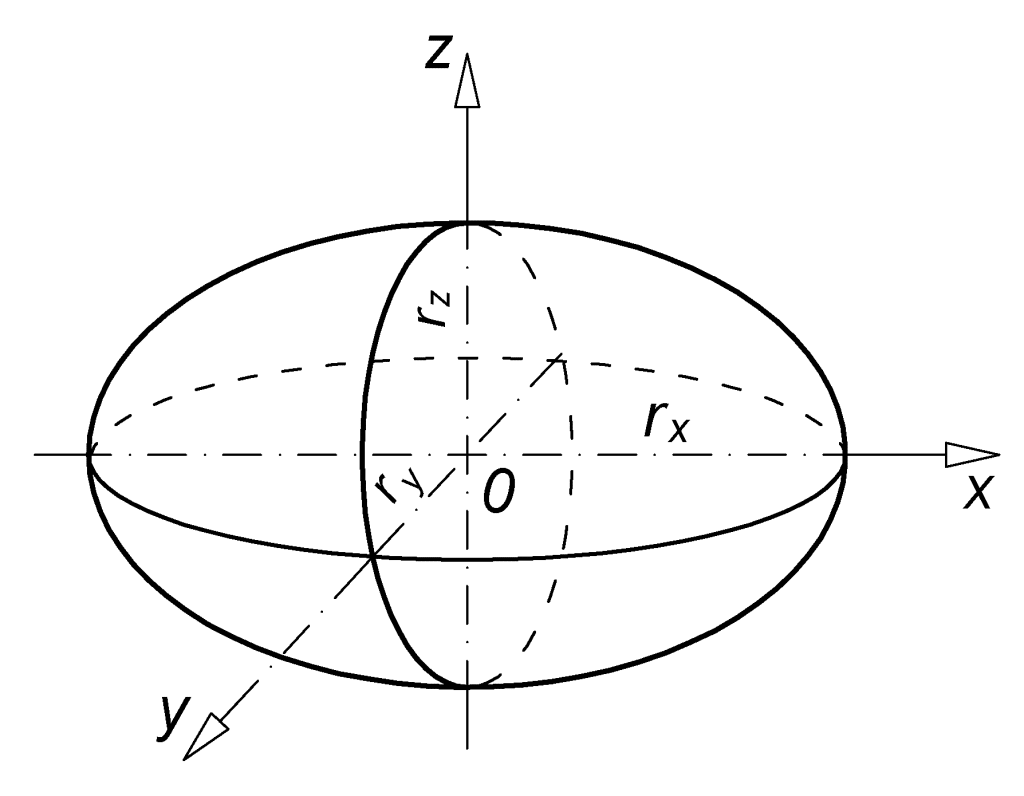postać parametryczna , gdzie: promienie: rx  po osi x,  ry po osi y,  rz  po osi z, wsp. geograficzne: φ szerokość,   λ  długość.	jeśli rx =ry z, to elipsoida obrotowa wydłużona; jeśli rx=ry > rz , to elipsoida obrotowa spłaszczona; powierzchnia nierozwijalna na płaszczyznę
Sfera		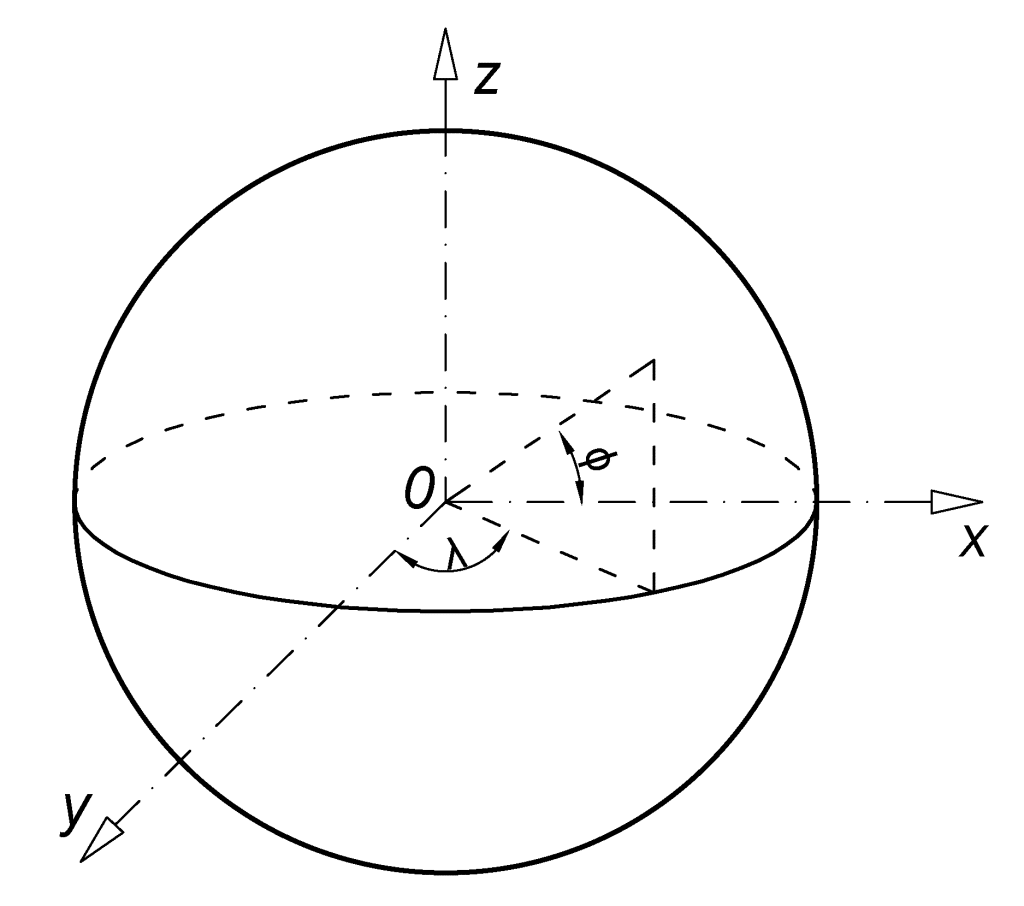	jśli rx=ry rz = r, to sfera o promieniu r; linie geodezyjne : okręgi (koła wielkie)
Paraboloida eliptyczna		postać parametryczna	inna postać powierzchnia translacyjna
Paraboloida hiperboliczna			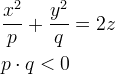inna postać lub powierzchnia translacyjna i prostokreślna
Hiperboloida dwupowłokowa		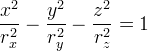postać parametryczna	dla rx =ry, hiperboloida dwupowłokwa obrotowa ; wierzchołki (0,0, ± r z)
Powierzchnie prostokreślne
Cykloid powierzchnia Catalana
Inne, bardziej znane powierzchnie
Torus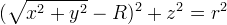
Helikoida
Konoid Plückera
Kuboida Ennepera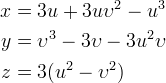
Powierzchnia Scherka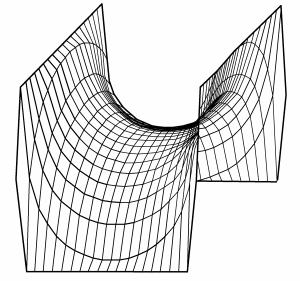
Powierzchnia Peano
Powierzchnia Kopiec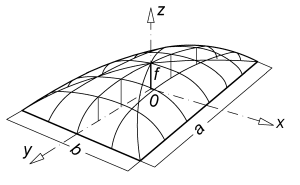

Paraboloida hiperboliczna

Ważną kwadryką  wymienioną w tab 1 jest paraboloida hiperboliczna, której płat jest często nazywany hyparem. Hypar jest powierzchnią translacyjną powstałą  przez równoległy ruch paraboli wklęsłej (tworzącej) po grzbiecie innej paraboli (prowadzącej), zwanej kierownicą, która jest prostopadła do tworzącej  (rys.2a). 

Rys.2 Hypar jest powierzchnią: a) translacyjną, b) prostokreślną

Przekroje pionowe hypara są parabolami, a poziome hiperbolami. Taka powierzchnia może być również utworzona przy przesuwaniu linii prostej wzdłuż dwóch innych prostych ustawionych skośnie do siebie i tworzącej, tak jak pokazano na rys. 2b. Jedną z głównych zalet hyparu jest właśnie to, że podwójna krzywizna może być zbudowana wyłącznie za pomocą liniowych elementów konstrukcyjnych (prętów), które tworzą w planie projekcję siatek z rombów.  W ten sposób jednowarstwowe hypary mogą być wykonane z prostych prętów, a dwuwarstwowych z kratownic o prostej osi.  Pojedyncze, rombowe oczko hypar nadaje się do zastosowania do budowy powłok w planie prostokątnym lub eliptycznym . W praktyce istnieje nieskończenie wiele sposobów łączenia elementów  hyparów w złożone kopuły.

Siatkowe  sklepienia beczkowe (ang. barrel vaults)

Początki kopuł siatkowych sięgają starożytności, gdy zaczęto stosować sklepienia beczkowe (inaczej kolebkowe) (ang. barrel vaults). Rzymianie rozwinęli sklepienia beczkowe do konstrukcji sklepień krzyżowych, a właśnie żebra w tych sklepieniach są prototypem prętów siatki sklepień oraz kopuł (powłok) siatkowych. 

Sklepienia beczkowe są rozpięte na jednokrzywiznowej powierzchni cylindrycznej. Krzywa poprzeczna jest najczęściej wycinkiem okręgu, choć stosuje się również parabole, elipsy lub krzywe łańcuchowe.
Typowe konstrukcje sklepień beczkowych zestawiono w tab.2 , a w tab.3. pokazano najczęściej stosowane typy siatek w sklepieniach.

Tab.2.  Konstrukcja sklepień beczkowych (opracowano na podstawie  [6]  

Nazwa	Rysunek	Uwagi
Sklepienia długie L/f > 5		L- długość sklepienia f- strzałka wyniesienia (wysokość) sklepienia Dla sklepień długich =(L/f>5), a nawet średnio długich (L/f>3) można stosować analogię belkową i traktować sklepienie jako belkę o długości L i zakrzywionym przekroju poprzecznym. Najczęściej jednak wprowadza się dźwigary brzegowe wzdłuż linii podporowych sklepienia, które odgrywają pierwszorzędną rolę w przenoszeniu obciążeń. Dźwigary brzegowe są kratownicami o długości L, które obciąża się reakcjami pionowymi ze sklepienia, które jest traktowane jako krótkie, czyli kształtowane w analogii łukowej. Reakcje poziome łuków (rozpór) należy przenieść przez sztywne słupy, posadzkę lub przypory, albo też zastosować ściągi bądź przepony sklepienia. W przypadku stosowania analogii belkowej należy też zwrócić, uwagę czy zachowane są warunki: zakres liniowo sprężystej pracy powłoki oraz symetryczne obciążenia poprzeczne i stały przekrój poprzeczny powłoki po długości belki- sklepienia.
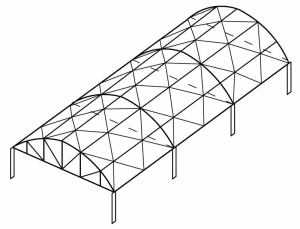
Sklepienia średnie 5/3  > L/f < 5		Dla sklepień średnich zachowanie konstrukcji jest skomplikowane: oba kierunki (podłużny-liniowy i poprzeczny -łukowy ) są równie ważne. W takim przypadku zaleca się stosowanie analiz dokładnych (za pomocą przestrzennych modeli komputerowych). Wprowadzanie brzegowych belek podłużnych najczęściej jest w tym przypadku nieoptymalne, a analogia belkowa w kierunku podłużnym lub łukowa w kierunku poprzecznym nie daje zadowalających rezultatów
Sklepienia krótkie 1/4  > L/f < 5/3		Krótkie sklepienia mogą być traktowane jak łuk, który w tym przypadku przejmuje  pierwszorzędną rolę w przenoszeniu obciążeń Zachowanie się łuków zależy od ich geometrycznych proporcji i objawia się przede wszystkim siłą rozporową, która powinna być przejęta przez przypory, ściągi lub posadzkę. Ciąg krótkich sklepień można uzyskać poprzez zagęszczenie przepon opartych na słupach (tak jak pokazano na szkicu wyżej), lub poprzez zwiększenie wyniesienia klucza łuku, czyli zwiększenie wysokości sklepienia f ( tak jak pokazano na szkicu obok).

Tab.3.  Typy siatek sklepień beczkowych (opracowano na podstawie  [6] 

Nazwa	Rysunek	Uwagi
Ortogonalna typ Warren		Pierwsze trzy rodzaje siatkowych sklepień (ortogonalne) powstawały poprzez różnicowanie ułożenia krzyżulców. Dopiero w roku 1892 Föppl dokonał istotnej modyfikacji, proponując siatkę trójdrożną (patrz niżej). Typ Warren nazwę zawdzięcza inżynierowi, który go opatentował w roku 1848 i jest znamienny tym, że krzyżulce są nachylone naprzemiennie i tak by największe siły wywoływały rozciąganie, a nie ściskanie.
Ortogonalna typ Pratt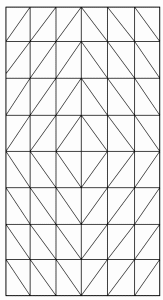		Typ Pratt nazwę zawdzięcza inżynierowi, który go opatentował w roku 1844 i jest znamienny tym, że krzyżulce są nachylone w tą samą stronę,
Ortogonalna typ X		W wykratowaniu typu X jeden z krzyżulców jest rozciągany, a drugi ściskany. Najczęściej dopuszcza się do wyboczenia krzyżulca ściskanego i przejęcia wszystkich sił przez krzyżulce rozciągane. Taki typ wykratowania jest inteligentny, ale kratownica jest statycznie niewyznaczalna z nieliniowością strukturalną i wymaga bardziej złożonych analiz mechanicznych.
Lamella		Popularne gwiaździste sklepienie tworzy siatkę w kształcie rombu.. Sklepienia lamella początkowo były wykonywane  z drewna, lecz wraz ze wzrostem rozpiętości, stosowano bardziej wytrzymałą stal. W celu zwiększenia stabilności sklepienia i zmniejszenia ugięcia od niesymetrycznych obciążeń zastosowano płatwie (podłużne kratownice). Stworzyło to bardzo popularny trójdrożny typ siatki  (poniżej ).
Trójdrożna Föppl		Siatka  Föppla składa się z prętów równoległych do osi sklepienia  rozpiętych pomiędzy przeponami szczytowymi. Pręty te podparte są bocznie przez krzyżulce, które łączą sąsiednie pręty podłużne, tworząc sklepienie siatkowe. Trójdrożny typ sitaki sklepienia zapewnia równomierny rozkład naprężeń i znacznie mniejsze ugięcia w przypadku niesymetrycznego obciążenia w stosunku do ugięć obserwowanych  przy innych typach siatki.  Przy dużych rozpiętościach siatkowe sklepienia jednowarstwowe  mają do niestabilności węzłów, zwłaszcza pod działaniem dużych niesymetrycznych obciążeń i dlatego należy stosować sztywne, a nie przegubowe węzły siatki. Trójdrożny typ siatki umożliwia budowę sklepienia przy wykorzystaniu równobocznych trójkątów złożonych z jednostek modułowych o identycznej długości krawędzi i ze stosunkowo  prostymi węzłami, co jest szczególnie chętnie wykorzystywane w przekryciach prefabrykowanych.

Makowski Z. [7] przedstawił współczesny stan  teorii i praktyki sklepień beczkowych w zastosowaniu do nowoczesnych konstrukcji siatkowych.

Kopuła siatkowa

Rodzaje siatek i plan kopuł

Uogólnieniem sklepień beczkowych na drugi wymiar są kopuły, które były stosowane od najdawniejszych czasów. Kopuły są obiektem zainteresowania architektów i inżynierów, bo umożliwiają osiągnięcie dużych rozpiętości przekrycia przy  małym zużyciu materiału. Taka optymalizacja jest możliwa poprzez przeważający udział naprężeń błonowych, co świadczy o tym, że są wynikiem ewolucji natury.

Stosowane są dwie formy powierzchniowe: lokalnie wypukłe (synklastyczne) oraz lokalnie siodłowe  (antyklastyczne). Kształty syklastyczne  mają powłoki: kuliste, paraboliczne lub eliptyczne. Kształty antyklastyczne mają powłoki hiperboloidalne. 

Siatki prętów rozpięte na kopułach mogą mieć rozmaite układy, ale w praktyce stosuje się sześć typów, pokazanych w tabeli 4, a mianowicie: kopuły żebrowane, Schwedlera, trójdrożne , lamella (równoległe i krzywoliniowe) oraz  geodezyjne.

Tab.4. Rodzaje siatek  kopuł  (opracowano  na podstawie [6]

Nazwa	Rysunek	Opis
Żebrowe		Najwcześniejszy typ usztywnionej kopuły, Składa się z wielu identycznych południkowych sztywnych łuków pełnościennych lub kratownicowych, połączonych w wierzchołku pierścieniem zaciskowym. Równoleżniki są elementami drugorzędnymi ukształtowanymi w formie koncentrycznych pierścieni. W rezultacie kształt sieci jest trapezowy. Może być wykonana ze stali, drewna lub żelbetu. Chętnie i często stosowana w historii architektury i konstrukcji ze względu na czysty układ - podział na łuki nośne i stężające pręty równoleżnikowe.
Schwedlera		Popularny typ sieci, wprowadzony przez Schwedlera już w 1863 roku. Składa się z prętów południkowych połączonych równoleżnikami, jak w kopułach żebrowych, ale z dodatkowym, ukośnym wykratowaniem każdego trapeza na trójkąty powłokowe. Stosuje się również wykratowanie krzyżowe trapezów powłokowych. W tym przypadku siatka prętów jest statycznie niewyznaczalna. Stosowane obecnie numeryczne metody analiz umożliwiają prostą analizę takich sieci, jak również sieci z węzłami sztywnymi , czyli systemu prętowego, w którym pręty przenoszą nie tylko siły osiowe ale również zginanie i skręcanie. Dodatkowe wykratowanie prowadzi do dużej odporności na działanie obciążeń niesymetrycznych. W przypadku wykratowania krzyżowego istotnie zwiększamy niezawodności kopuły o raz zmniejszamy wrażliwość na przeskok węzłów.
Trójdrożne		Sieć trójdrożna w kopułach jest uogólnieniem siatki trójkierunkowej w sklepieniach. Jest stosowana zarówno w kopułach jednowarstowych jak i dwuwarstwowych. System trójdrożny został rozwinięty i opatentowany przez japońską firmę Tomoegumi Iron Works pod nazwą ‘‘Diamond Dome’’ ("Diamentowa kopułka '') Chętnie stosowane ze względu na równomierny rozkład sił (i materiału) w przypadku niesymetrycznego obciążenia. Wdrożono kilka praktycznych systemów kopuł trójdrożnych.
Lamella równolegle		Sieć Lamelia tworzy przecinające się dwukierunkowo pręty ukośne, tworząc siatkę w kształcie rombu, podobnie jak w siatce Lamella w sklepieniach kolebkowych (pkt.2). Każdy element rombowy ma dwa boki, z których jeden jest dwa razy dłuższy od drugiego. 'Siatki Lamella mogą być rówolegle lub zakrzywione. Siatka równoległa jest konstruowana na planie kołowym, podzielonym jest na kilka sektorów ( zwykle sześć lub osiem) , a każdy sektor jest podzielony równolegle do żeber siatki rombu o tej samej wielkości. Elementy tworzą diamentowy wzór, zastosowany w dwóch pierwszych wielkich stadionach sportowych USA: Houston Astrodome (1962/64) , o rozpiętości 196 m i Superdome w Nowym Orleanie (1973) , o średnicy 207 m. Typ kopuł Lamella bardzo popularny w USA i nazywany Kiewitt ,
Lamella zakrzywione		W zakrzywionej sieci Lamella zastosowano sieć rombów o różnych rozmiarach , stopniowo wzrastających od środka kopuły. Oczka rombowe są tworzone przez ukośne żebra wzdłuż linii promieniowych. czasami poprzez wprowadzanie płatwi opartych na koncentrycznych pierścieniach są tworzone oczka trójkątne. Ponieważ pręty w każdym pierścieniu równoleżnikowym są równe, więc czas wytwarzania jest krótki, a montaż łatwy. Powszechnie uważa się, że ze względu na swoje piękno - nie są dostatecznie docenione w architekturze i niesłusznie wyparte przez kopuły geodezyjne.
Geodezyjne		Siatki geodezyjne zostały opracowane B. Fullera, który uwypuklił zalety kopuł siatkowych, w których elementy główne leżą na dużym okręgu sfery i wprowadził nazwę geodezyjne. Powierzchnią bazową jest sfera, na której rozpięto siatkę trójdrożną złożoną z trójkątów sferycznych. Oryginalne kopuły Fullera były tworzone z dwudziestościanu jako bryły wyjściowej do aproksymacji sfery. Fuller opracował kilka metod podziału sfery na trójkąty sferyczne, które krótko omówiono w kolejnym rozdziale pracy Praktyka pokazuje, że układ sieci uzyskany z podziału geodezyjnego nie jest wystarczający, ponieważ prowadzi do przenicowania elementów i są wymagane pręty dodatkowe. W wyniku wprowadzenia dodatkowych prętów powstałe trójkąty nie są już równoboczne. Wraz ze wzrostem stopnia aproksymacji sfery i zmniejszaniem boków krawędzi, zwiększa się liczba różnych prętów i węzłów, co wpływa na wzrost kosztów kopuły. Kopuły geodezyjne są bardzo ekonomiczne dla mniejszych rozpiętości z powodu małej liczby różnych prętów i węzłów. Dla dużych rozpiętości często stosuje się inne typy siatek.

Kopuły buduje się na planie  koła,elipsy, prostokąta lub wielokąta. W tab. 5 pokazano kilka często stosowanych układów.

Tab.5.  Plan kopuł (opracowano  na podstawie [8] 

Nazwa	Rysunek	Uwagi
Plan koła Kopuła średniowyniosła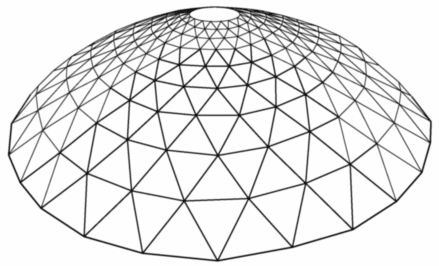		Najczęściej stosowany plan kopuł. Przy planie centralnym wykostruoawany jest otwór pod latarnię.
Plan koła Kopuła wyniosła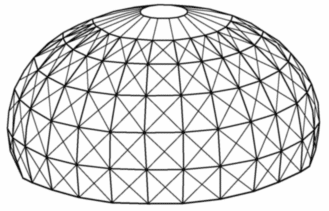		Kopuła wyniosła zachowuje się lepiej od małowyniosłej , ze wzgledu na lepsze wykorzystanie "efektu kopuły" i małą wrażliwość na przeskok węzłów.
Plan elipsy Kopuła porcelankowa		Plan kopuł chętnie stosowany współcześnie wraz z nadaniem dynamicznego kształtu kopule
Plan prostokąta Kopuła płaska		Plan dostosowany do kształtu przekrywanego obszaru. Wrażliwa na przeskok węzłów i praktycznie nie jest stosowana jako jednopowłokowa, a jeśli, to jako ruszt z zakrzyowionych belek *łuków)
Plan sześciokąta Kopuła płaska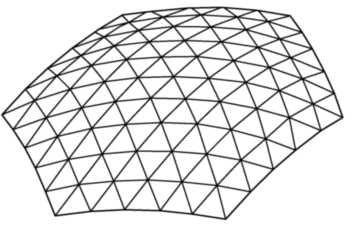		Konstrukcja umożłiwiająca zmianę planu z kołowego na wielokątny, w przykładzie na sześciokątny
Plan wielokąta Kopuła cykloidalna		Kopuła cykloidalna jako wynik sklejenia kopuł walcowych (patrz niżej) lub jako wynik przejścia z planu kołowego na wielokątny.

 Ważną realizacją kopuły siatkowej  jest kopuła pawilonu  na  pierwsze Międzynarodowe Targi Maszynowe w Brnie  zrealizowana już w 1959 roku (konstrukcja: Ferdynand Lederer) [9] . Na rys.3 pokazano fotografię obiektu (3a) i oryginalny projekt (3b).  Kopuła jest rozpięta na czaszy kulistej o średnicy zewnętrznej 122 m i wysokości (poziom świetlika) 46 m. Kopułę wieńczy okulis o średnicy 18 m.

Rys. 3a Kopuła Lederera Brno (1958)   [10]

Rys 3b. Kopuła pawilonu Z w Brnie (Lederer, 1958)

Kopuła geodezyjna

Na rys. 3 i 4 pokazano jedne z pierwszych kopuł geodezyjnych zrealizowanych w połowie XX wieku po spopularyzowaniu idei ich stosowania przez R. B. Fullera [11], a mianowicie:
1) Climatron, gigantyczny klimatyzowany ogród botaniczny  w St. Louis w stanie Missouri, wybudowany w konstrukcji stalowej w roku 1960 (rys.3 ),
2)  Sports Arena Astrodome w Houston w Teksasie, wybudowany w roku 1965 (rys.4 ).

Rys.3. Pierwsza kopuła geodezyjna. Botaniczny ogród Climatron, St Louis USA (1960) [12]

Rys.4. Sports Arena Astrodome Houston USA (1965) [13]

Dalsze informacje podano w artykule kopuły geodezyjne.

Przecięcia i sklejanie kopuł

Literatura

1. Bryła W. (1910), Obliczanie kopuł płaszczowych. Czasopismo Techniczne, 2
2. Föppl A. (1892), Das Fachwerk im Raume, B.G. Teubner
3. Pawlikowski P. (2015), Spiralny świat muszli. Wrocławski Portal Matematyczny, [http://www.matematyka.wroc.pl/matematykawsztuce/spiralny-swiat-muszli ]
4. Pawlikowski P. (2015), Pięciokąty foremne w ogrodzie , Wrocławski Portal Matema-tyczny, [ http://www.matematyka.wroc.pl/matematykawsztuce/zloty-podzial-w-przyrodzie ]
5. Sikora A. (2012, April 20). Architektura organiczna, cz. IV, Blobitektura. PROGG, [ http://progg.eu/architektura-bioekstensywna/ ]
6. Lan T. T. (2005). Space Frame Structures. In W.- F. Chen, E. M. Lui (Eds.), Handbook of Structural Engineering (2nd Ed.), CRC Press
7. Makowski Z. S. (2006), Analysis, Design and Construction of Braced Barrel Vaults. Taylor&Francis, Elsevier Applied Science Publishers Ltd, Chapman & Hall Publishers
8. Kowal Z. (1982). Hale o dużych rozpiętościach. W: Bogucki W. (red.), Poradnik pro-jektanta konstrukcji metalowych (1 Wydanie., 2 Tom). Arkady
9. Chodor L. (2013). Kopuły w architekturze, Wykład 4 z przedmiotu Konstrukcje bu-dowlane 2 dla Architektów, Politechnika Świętokrzyska, Kielce, [ https://chodor-projekt.net/wp-content/uploads/PIPress/Wyklady/KB2/4-(2015)-KB2-Kopuly-w-architekturze.pdf ]
10. Wikipedia,(2015). Pavilion Z, Brno Exhibition Grounds, [ http://www.anc-d.u-fukui.ac.jp/~ishikawa/years/1950-1960/Structural%20Systems-Countries/Axial%20Force/Europe/1959-s.f-CZE/PavilionZ,ExhibitionGrounds.htm ]
11. Weston R. (2011), 100 Ideas that Changed Architecture. Lurence King Publishing Ltd., London
12. Wikipedia,(2014), Climatron, [ https://en.wikipedia.org/w/index.php?title=Climatron&oldid=599090514 ]
13. Wikipedia. (2015). Astrodome, [ https://en.wikipedia.org/wiki/Astrodome#/media/File:Reliant_Astrodome_in_January_2014.jpg ]
14. Korn T., M. (1983), Matematyka dla pracowników naukowych i inżynierów (Tom. 1, 2), PWN, Warszawa
15. Makowski Z. S. (1984), Analysis, Design and Construction of Braced Domes. Nichols Publishing Company, Granada Publishing

________________________________