Uwaga: artykuł jest w trakcie edycji . Zawiera treści tymczasowe.  

Niniejszy artykuł jest rozdziałem 2-2 podręcznika Imperfekcyjna metoda projektowania konstrukcji [ ← spis treści]
Nawigacja: [Imperfekcje i ich źródła] ⇐  ⊗  ⇒ [ Geneza metod imperfekcyjnych]

Artykuł w ciągu ostatnich 24 godzin czytało 1 Czytelników

[ Fundamentalne założenia metody imperfekcyjnej ] ⇐ ⊗ ⇒ [ Proces stochastyczny imperfekcji systemowych ]

Wprowadzenie

Klasyfikację imperfekcji konstrukcji przedstawiono w rozdziale 2 i na rys. 2.1. Systemowe geometryczne imperfekcje konstrukcji dotyczą elementu EGI lub układu UGI.

Imperfekcje układu UGI są często nazywane globalnymi lub przechyłowymi, ponieważ wynikają z odchyleń położenia węzłów systemu od położenia oczekiwanego, przy czym z punktu widzenia stabilności konstrukcji najistotniejsze są odchylenia poziome (przechyły) lub skręcenia całej konstrukcji. Najczęściej będziemy analizowali imperfekcje przechyłowe, które wynikają z odchylenia (lub przechylenia) węzłów powierzchniowych od zamierzonego położenia projektowanego, w tym odchylenia punktów przyłożenia sił powierzchniowych czynnych lub biernych ( reakcji podpór).

Pomiędzy węzłami systemu definiowane są elementy, które mogą być obarczone imperfekcjami teoretycznej (najczęściej prostej) osi rozpiętej pomiędzy węzłem początkowym i końcowym elementu. Imperfekcje elementu EGI często są nazywane lokalnymi lub łukowymi, wynikają z odchylenia linii pręta lub powierzchni pomiędzy węzłami systemu od kształtu oczekiwanego. W systemie często definiuje się grupy elementów (superelementy), które mogą mieć odchylenia łukowe grupy, a niezależnie każdy element może mieć swoje imperfekcje łukowe, wynikające z odchylenia położenia zdefiniowanych węzłów wewnątrz konstrukcji od położenia projektowanego. Dlatego imperfekcje łukowe przypiszemy do elementu EŁI  lub do systemu SŁI 

Najczęściej te odchylenia mają kształt kolebkowy (łukowy w przypadku konstrukcji liniowych). Imperfekcje lokalne występują pomiędzy zdefiniowanymi węzłami wewnętrznymi i w zależności od typu elementu mogą być łukowe w przypadku elementów prętowych (jednowymiarowych) lub powłokowe, w przypadku elementów powierzchniowych (płyt, tarcz, powłok).

W rozdziale 2 „Efekt P-δ”, pokazano, że działanie sił osiowych na łukowych imperfekcjach prowadzi do amplifikacji przemieszczeń, a w konsekwencji również sił przekrojowych, co nazywa się efektem P-δ, lub P- „małe delta”. Na rys. 4-2.1 pokazano, że również działanie siły pionowej P na imperfekcji przechyłowej Δ również prowadzi do zwiększenia momentów zginających pręt .  Taki efekt nazywa się P-Δ, lub P- „duże delta”

Efekty P-Delta prowadzą z jednej strony do zwiększenia sił i przemieszczeń lub z drugiej strony do zmniejszeniu wytrzymałości konstrukcji rozpatrywanej w konfiguracji nieodkształconej.

Imperfekcje przechyłowe a efekt P-Δ

Efekt  P-Δ i P-δ

Efekt P-Δ (lub P- „duże-delta”) jest związany z względnymi przemieszczeniami końców elementu (przechyłem). W przeciwieństwie do P-δ, ten typ efektu P-Delta ma decydujące znaczenie dla modelowania i analizy nieliniowej. W rezultacie efektywna sztywność boczna zmniejsza się we wszystkich fazach odkształcenia [1] .
Szczególnie ważny jest efekt działania obciążeń grawitacyjnych na przemieszczone bocznie wysokie budowle, w tym wielopiętrowe budynki.

Rys.4-2.1. Efekt P-δ i P-Δ: a) schemat, b) rozkład momentów zginających A- z analizy I – rzędu, B – efekt P-Δ, C- efekt P-δ

Przekształcenie efektu P- δ w P-Δ

Często, w celu zwiększenia efektywności obliczeń (niewielkie zwiększenie czasu obliczeń przy dostatecznej dokładności z punktu widzenia praktyki), szczególnie w obliczeniach sejsmicznych stosuje się aproksymację, zmierzającą do sprowadzenia efektu P- δ do analizy efektu P-Δ poprzez podział istotnych elementów konstrukcji na wiele segmentów. [2] .

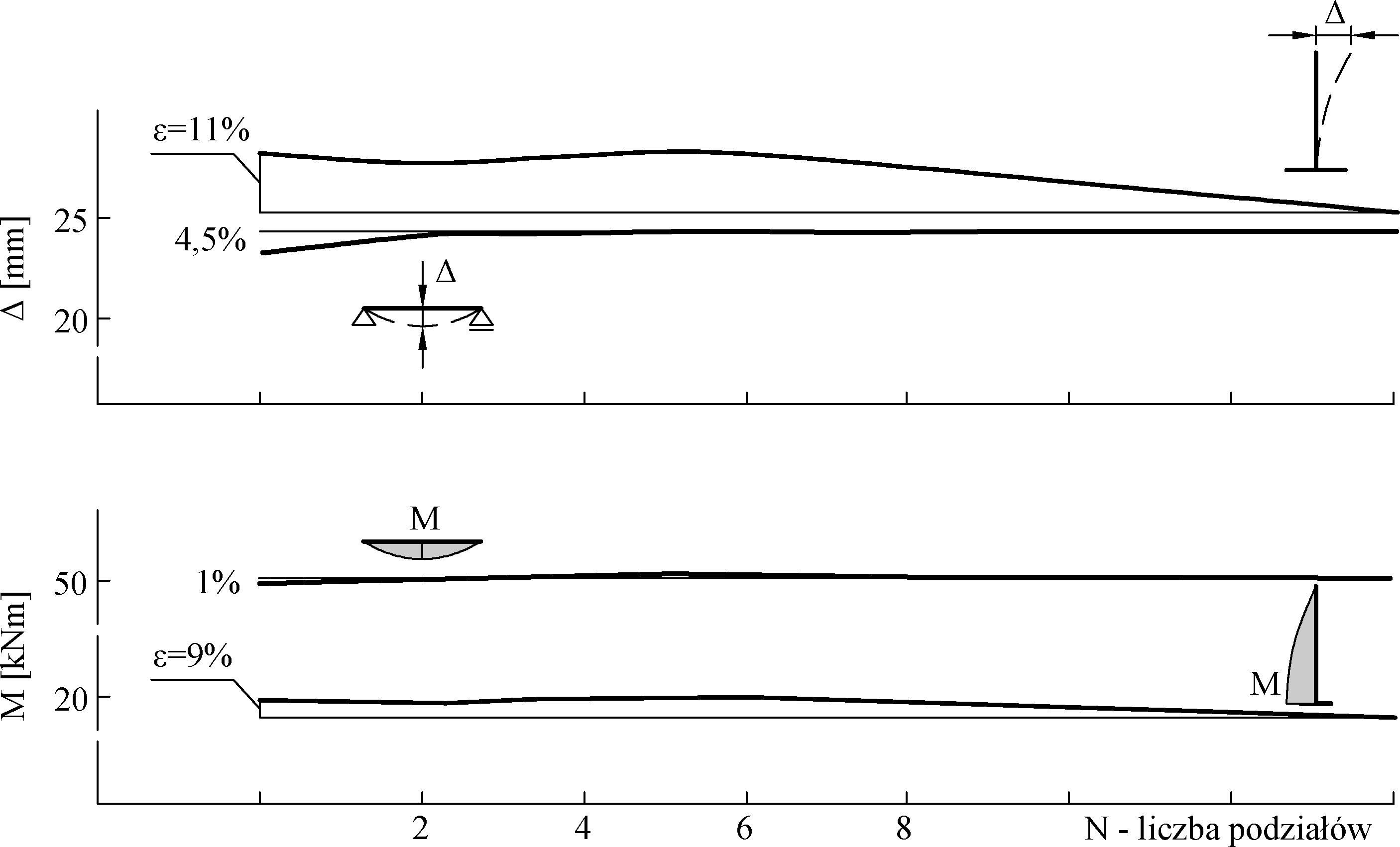
Wpływ aproksymacji imperfekcji łukowych na sprawcze przemieszczenia Δ oraz sprawcze momenty zginające M przedstawiono na Rys. 4-2.2. Wykres prezentuje wyniki uzyskane w przykładach 6.1.1 oraz 6.1.2 (rozdział 6), gdzie zamieszczono szczegółowy opis.  Błąd aproksymacji ε jest największy przy podziale pręta na dwa proste elementy, czyli zamodelowaniu jednego węzła w środku elementu „wypchniętego” z osi pręta o strzałkę imperfekcji $e_0$ . Aproksymacja poprawia się wraz z zagęszczaniem podziału. Węzły dodatkowe umieszczane były na łuku sinusoidy. Znacznie lepsze wyniki aproksymacji obserwuje się dla pręta przegubowo-przegubowego niż dla wspornika) i dla momentów zginających 2 rzędu niż dla przemieszczeń sprawczych. Błąd aproksymacji momentu nie przekracza 10% dla wspornika i 1% dla pręta przegubowo-przegubowego.

Rys.4-2.2. Przemieszczenie sprawcze w funkcji aproksymacji imperfekcji łukowej

Z analizy przykładu wynika, że w przypadku układów przesuwnych (np. wspornika) pręty modelować elementami 9-cio węzłowymi (podział na 8 odcinków), natomiast w układach nieprzesuwnych (np. belka na nieprzesuwnych podporach) wystarczają już 4 węzły pośrednie. W celu wyeliminowania błędu aproksymacji należałoby stosować elementy zakrzywione o przekroju zwartym ( Dodatek  C) lub ogólniej o przekroju cienkościennym.

Aproksymacja imperfekcji łukowej łańcuchem elementów

Aproksymacja imperfekcji łukowej łańcuchem prostych elementów jest w istocie przekształceniem efektu P- δ w P-Δ.

Aproksymacja polega na zmianie geometrii nominalnie prostego pręta w łańcuch kilku prostych elementów z węzłami ułożonymi na łuku imperfekcji, najczęściej na sinusoidzie $e(x)=e_L \cdot sin( \pi x / L)$ z amplitudą $e_L$ dla $x=L/2$, gdzie $x$ jest bieżącą współrzędną pierwotnego elementu o długości $L$ z węzłem początkowym dla $(x=0)$ i końcowym dla $(x=L)$.

Przyjmuje się nieparzystą liczbę węzłów pośrednich, ze środkowym węzłem w przekroju sprawczym S, co daje parzystą liczbę prostych odcinków łańcucha. Na Rys.4-2.5d pokazano najprostszy łańcuch dwuelementowy z jednym węzłem pośrednim.

Analizę błędu aproksymacji dla łańcucha o różnej liczbie elementów przedstawiono wyżej (rys. 4-2.2).

W wielu programach komputerowych (np. Consteel [3] , SAP2000 [4] i in) imperfekcje łukowe są uwzględniane poprzez zmianę geometrii sytemu w trakcie generowania obliczeniowego modelu elementów skończonych. Podczas dyskretyzacji węzły przesuwane są o odpowiednie offsety  tak by leżały na łuku imperfekcji. Liczba segmentów łańcucha wynika z liczby węzłów pośrednich, przyjętych, jako parametr dyskretyzacji w programie obliczeniowym (czyli domyślnie cztery – w przypadku układów przesuwnych należy zwiększyć).

Efekty P-Delta geometrycznych imperfekcji systemowych należy analizować w ramach teorii geometrycznie nieliniowej, przy czym powszechnie przyjmuje się, że można poprzestać na analizie. 2 rzędu. Stopień geometrycznej nieliniowości teorii jest stopniem aproksymacji nieliniowej sztywności w rozwinięciu w potęgowy szereg Taylora wokół punktu początkowego konfiguracji konstrukcji. Zachowanie tylko członów liniowych (linearyzacja) prowadzi do klasycznej teorii 1 rzędu, a zachowanie kolejnych potęg w rozwinięciu określa kolejne teorie: 2, 3 rzędu itd.

Wpływ rzędu (stopnia) nieliniowości teorii na efekty P-Delta zbadamy w drodze analizy ściśle nieliniowego modelu systemu złożonego z krępych prętów. Zweryfikujemy założenie o wystarczalności analizy 2 rzędu. Nie zajmujemy się prętami uogólnionymi ze stopniem swobody paczenia, co nie zmniejsza ogólności rozważań.

Podstawy teoretyczne ściśle nieliniowej teorii prętów o przekroju zwartym zaprezentowano w Dodatku C.
Niżej szczegółowo przeanalizujemy wspornik, który jest przedstawicielem układu przesuwnego i pręt przegubowo-przegubowy, który jest przedstawicielem układu nieprzesuwnego.

Układ przesuwny

Poniższe formuły ($\ref{4-2.5}$) do ($\ref{4.6}$) uzyskano na gruncie teorii geometrycznie ścisłej, przestawionej w  Dodatku C. Zdefiniowane tam nieliniowe sztywności, zależą od współczynnika wytężenia siłą osiową, wyznaczanego z zależności:

$$\begin{equation} \alpha=\cfrac{\pi}{2} \sqrt{\cfrac{N}{N_{cr}}}= \cfrac{L}{2} \sqrt{ \cfrac{N}{EI}} \label{4.7} \end {equation}$$

gdzie $N_{cr}$ – siła krytyczna (1.4) dla $L_{cr} = L$.

Przemieszczenie  $\Delta$ głowicy oraz moment zginający utwierdzenie $M$ (przy podporze wspornika) pokazanego na Rys.4-2.1, wynosi:

• od obciążenia skupionego $H$ w wierzchołku

$$\begin{equation} \Delta_H=\cfrac{HL^3}{3 \Theta} [\Lambda_4^2 -\Lambda_3\cdot(4 \Lambda_3 +c_\varphi) ]\label{4-2.5} \end {equation}$$

$$\begin{equation}  M_H=\cfrac{HL}{ \Theta / EI }\cdot  \Lambda_2 \cdot c_\varphi \cdot (  \Lambda_4 – 2 \Lambda_3)\label{4-2.3} \end {equation}$$

• od obciążenia rozłożonego $h$ :

$$\begin{equation} \Delta_h=\cfrac{h L^4}{24 \Theta} [ 4 \Lambda_4^2 – 16 \Lambda_2 +c_\varphi (\Lambda_2 -4 \Lambda_3) ]\label{4-2.4} \end {equation}$$

$$ \begin{equation}  M_h=\cfrac{h L^2}{ 12 \cdot  \Theta / EI }\cdot [4  \cdot (2  \Lambda_3 -\Lambda_4) \cdot (2 \Lambda_1 \Lambda_3 + \Lambda_1  \Lambda_4 – 3 \Lambda_2^2 ) +c_\varphi \cdot (3 \Lambda_2^2 – 12 \Lambda_2 \Lambda_3 – 2 \Lambda_1 \Lambda_4 + 6 \Lambda_1 \Lambda_4]  \label{4.6} \end {equation}$$

Współczynnik $c_\varphi $  jest bezwymiarowym współczynnikiem sprężystości podpory, określonym na podstawie konwencjonalnej stałej sprężystości $C_\varphi$ [kNm/rad] , to jest wartości momentu, odpowiadającej jednostkowemu obrotowi węzła.  W normie [5] sztywność obrotową węzła oznaczono jako $S_j$ , która w początkowej fazie pracy węzła wynosi $S_{j, ini}$ .

Pomiędzy sztywnością początkową $S_{j, ini} =C_\varphi $ oraz sztywnością względną $c_\varphi$ występuje związek

$$\begin{equation}  c_\varphi = \cfrac{S{j,ini} \cdot L }{EI}\label{4.8} \end {equation}$$

Podstawy słupów można klasyfikować jako sztywne, gdy spełnione są następujące warunki [5],kl. 5.2.3.5 (2) :

w ramach stężonych, czyli takich w których , których układ stężeń redukuje poziomy przechył, co najmniej 80% i w których wpływ deformacji może być pominięty i jednocześnie gdy smukłość względna $\overline \lambda_b$  elementu traktowanego jak przegubowo- przegubowy ($L_{cr}=L$) spełnia warunek

$ \overline \lambda_b \le 0,5$.

Dla smuklejszych elementów powinno zachodzić:

gdy $ 0,5 < \overline \lambda_b < 3,93 \to  S_{j,ini} \ge 7\cdot ( 2 \cdot \overline \lambda_b -1) EI/L$,

gdy $\overline \lambda_b \ge 3,93 \to $ $S_{j,ini} > 48 EI/L$

w ramach niestężonych ( w pozostałych przypadkach)

gdy $S_{j,ini} <  30  EI/L$

Wynika stąd, że w układach przesuwnych pełne utwierdzenie słupa w fundamencie może wystąpić dopiero wówczas, gdy

$$\begin{equation}  c_\varphi >  c_{\varphi,lim}= 30  \label{4.8a} \end {equation}$$

W Tab. 4-2.1 zestawiono współczynniki rozwinięcia w szereg potęgowy Taylora podług potęg „i” współczynnika $\alpha$, unormowanych funkcji ($\ref{4-2.5}$) do ($\ref{4.6}$). W kolumnach (3) do (6) podano wartości podzielone przez normę podaną w kolumnie (2), która jest odpowiednim efektem teorii pierwszego rzędu.

Tab. 4-2.1. Współczynniki $c_i$ rozwinięcia sprawczego przemieszczenia  i momentu zginającego  wspornika
w szereg Taylora podług potęg $\alpha$.  Współczynniki unormowane do  efektów 1 rzędu i

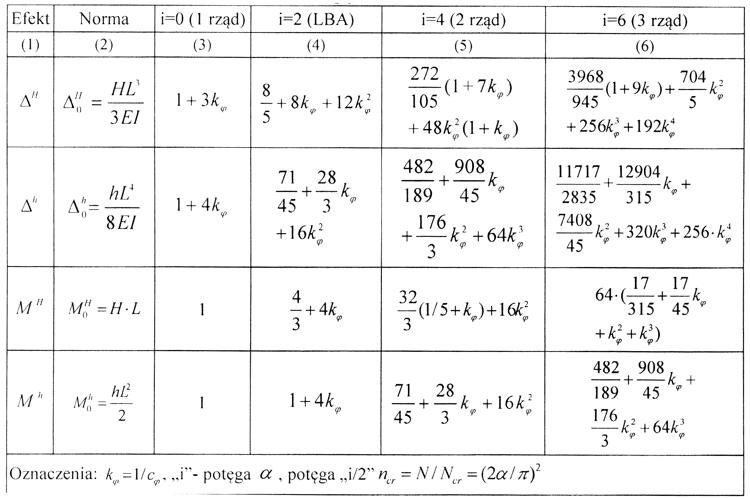
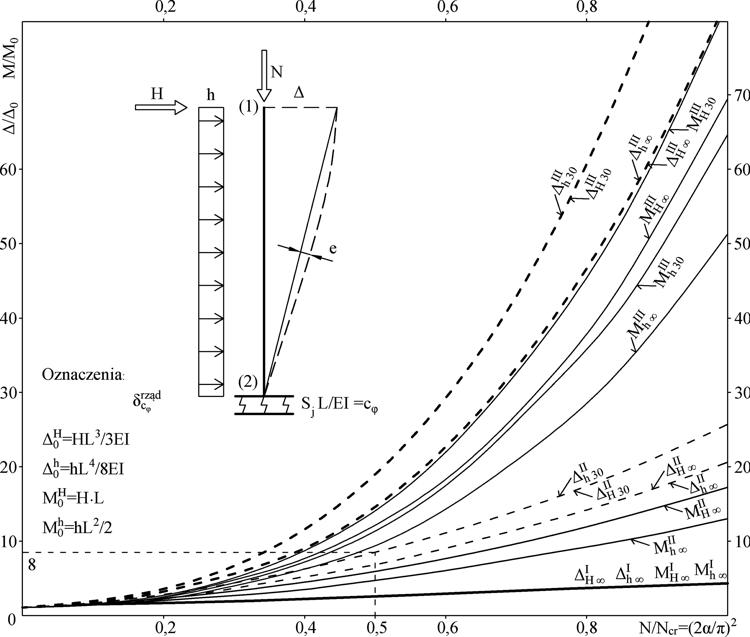
Na Rys.4-2.1 przedstawiono wykresy funkcji z Tab. 4-2.1. Na osi rzędnych naniesiono względną, krytyczną siłę osiową $n_{cr}=N/N_{cr}= (2\alpha/\pi)^2$, a na osi rzędnych współczynnik zwiększenia efektu w stosunku do efektu pierwszego rzędu. Dolny indeks „30” danej wielkości oznacza wartość uzyskaną przy sprężystości utwierdzenia słupa, czyli przy podatności $k_\varphi=1/30=0,03$, co odpowiada granicznej sztywności $c_ {\varphi,lim} $ ($\ref{4.8a}$). Wielkości z indeksem $\infty$  uzyskano dla teoretycznie pełnego utwierdzenia słupa $c_\varphi= \infty \to  k_\varphi =0$

Wnioski

• Stopień utwierdzenia słupa w fundamencie ma istotny wpływ na przemieszczenia. Na przykład przy obciążeniu słupa siłą ściskającą współczynnik  stosunku wychylenia końca wspornika  (3.rzędu) w stosunku do wychylenia 1. rzędu , przy pełnym utwierdzeniu (  ) wynosi 15, a dla równoważnie dopuszczonego przez normę [N25] , wynosi 19, czyli błąd oszacowania wynosi 27%,

Rys. 4-2.3 Słup wspornikowy Efekt P-Δ i P-δ  (opracowanie własne)

Wnioski

1. Stopień utwierdzenia słupa w fundamencie ma istotny wpływ na przemieszczenia.
   Na przykład przy obciążeniu słupa siłą ściskającą $N=0,5 N_{cr}$  stosunek $\Delta/ \Delta_0$  wychylenia końca wspornika  wg teorii 3.rzędu) $\Delta$ w stosunku do wychylenia 1. rzędu  $\Delta_0$ , przy pełnym utwierdzeniu ( $c_\varepsilon =\infty$) wynosi 15, a dla równoważnie dopuszczonej przez normę sztywności (c_\varepsilon =30)$ wynosi 19, czyli błąd oszacowania wynosi 27%,
2. Stopień utwierdzenia słupa w fundamencie ma istotny wpływ na powstający w utwierdzeniu moment zginający, nawet dla słupa statycznie wyznaczalnego, przy czym moment utwierdzenia zwiększa się wraz ze zmniejszaniem się sztywności podpory, na skutek zwiększania się momentu drugiego rzędu, choć na skutek osłabienia oporu węzła zwiększenie jest mniejsze od przyrostu przemieszczenia.
   Na przykład przy $N=0,5 N_{cr}$  współczynnik $M/M_0$ zwiększenia momentu utwierdzenia $M$ w stosunku do momentu 1. rzędu  $M_0$ przy pełnym utwierdzeniu wynosi 12 od obciążenia H i 9 od obciążenia h, a przy c_\varepsilon =30$ 14 i 11 odpowiednio, czyli błąd oszacowania wnosi 17% i 22% odpowiednio.
3. Przemieszczenia oszacowane wg teorii 2. rzędu są obarczone bardzo dużym błędem.
   Na przykład przy $N=0,5 N_{cr}$  współczynnik $\Delta/ \Delta_0$ dla  $c_\varepsilon =30$, wg teorii drugiego rzędu wynosi 8, a wg teorii trzeciego rzędu wynosi 19, czyli błąd oszacowania wynosi 237%.
4.  Siły przekrojowe oszacowane wg teorii 2 rzędu są obarczone bardzo dużym błędem.
   Na przykład przy $N=0,5 N_{cr}$ i $c_\varepsilon =30$ stosunek $M/M_0$ :
   – od obciążenia H wg teorii 2. rzędu wynosi 6, a wg teorii 3. rzędu wynosi 14, czyli błąd oszacowania 233%
   – od obciążenia h wg teorii 2. rzędu wynosi 5, a wg teorii 3. rzędu wynosi 11, czyli błąd oszacowania 220%.

Układ nieprzesuwny

Układ nieprzesuwny jest reprezentowany przez prostą belkę na sprężystej podporze, charakteryzowanej współczynnikiem sprężystości $C_\Delta\, [kN/m]$, lub współczynnikami rosną : sztywności $c_\Delta=\cfrac{C_\Delta}{EI L^3}$ lub podatności $k_\Delta =1/ c_\Delta $, które modelują stopień nieprzesuwności układu. Podpora jest niepodatna jeśli  $c_\Delta = \infty$.

Rys.4-2.4. Nieliniowa geometrycznie belka-słup (opracowanie własne)

W Dodatku C uzyskano  obliczono  ścisłą strzałkę ugięcia belki – słupa pokazanej na Rys.4-2.4:

$$\begin{equation}   \cfrac{ qL^4}{EI}\cdot \left(  \cfrac{1}{8} + \cfrac {12 (2 \Lambda_3 + \Lambda_4) }{36 \Lambda_2^2 +(c_\Delta \cdot 12 \Lambda_1)\cdot( 2\Lambda_3+ \Lambda_4}+ \cfrac{\alpha \cdot  tg\alpha/2}{2 \Lambda_3+\Lambda_4}\right) \label{4.9} \end {equation}$$

Podstawiając do ($\ref{4.9}$) wyrażenia  na nieliniowe funkcje $\Lambda_i (i=1,2,3,4) –Dodatek C uzyskamy:

$$\begin{equation}   \delta= \cfrac{5q L^4}{384 EI}\cdot \cfrac {4 \alpha^4  + 8 c_\Delta -\alpha^2 (128+c_\Delta)+ 8 ( 4\alpha^2 -c_\Delta ) / \sin{\alpha}} {20 \alpha^4 -5 \alpha^2 c_\Delta} \label{4-2.10} \end {equation}$$

a po rozwinięciu w szereg Taylora podług  $\alpha$ wokół  $\alpha=0$:

$$\begin{equation}   \delta=\cfrac{5q L^4}{384 EI}\cdot \left [ 1+ \cfrac{96}{5 c_\Delta} +\left (  \cfrac{1}{3}+\cfrac{384}{5 c_\Delta ^2}\right ) \alpha^2 + \left( \cfrac{ 61}{450} + \cfrac {1536}{5 c_\Delta^3} \right) \alpha^4 + \left ( \cfrac{277}{5040} + \cfrac{6144}{5 c_\Delta^4} \right ) \alpha^6  \right ] + …\label{4-2.11} \end {equation}$$

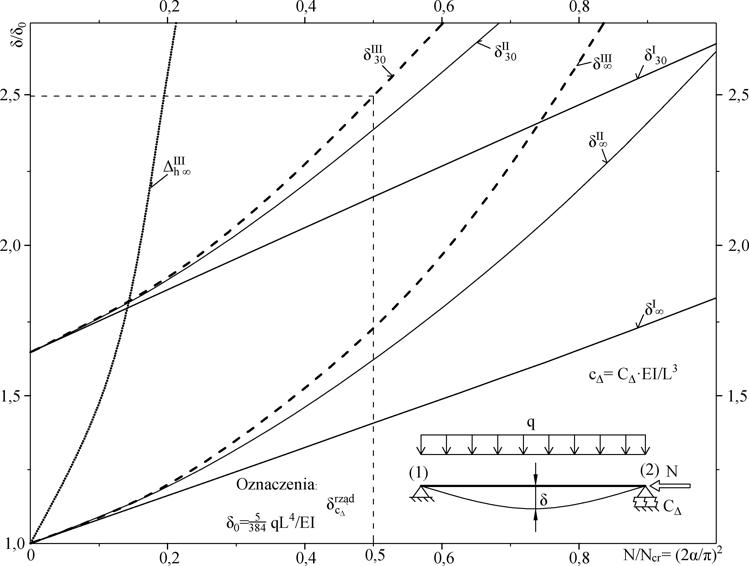
Wykres zależności ($\ref{4-2.11}$) znormalizowanej do ugięcia liniowego belki $\delta_0 = \cfrac{5 q L^4}{384 EI}$ pokazano na Rys.4-2.4. Indeksem „30” oznaczono wielkości uzyskane dla sprężystości podpory $c_\Delta =30$, czyli podatności $k_\Delta=1/30=0,03$. Indeksem $\infty$ oznaczono wielkości uzyskane dla teoretycznie niepodatnej podpory (c_\Delta = \infty ).

Z wykresu wynikają wnioski:

1. Wpływ nieliniowości jest prawie o rząd mniejszy w układach przesuwnych (linia kropkowa przeskalowana z Rys.4-2.3) w stosunku do wrażliwości układów nieprzesuwnych (pozostałe krzywe).
2. Przemieszczenia oszacowane wg teorii 2. rzędu są obarczone dużo mniejszym błędem niż w układach przesuwnych.
   Na przykład przy i  współczynnik  wg teorii 2. rzędu wynosi 2,4, a wg teorii III rzędu o 4% więcej,, podczas gdy w przypadku układu przesuwnego oszacowania wychylenia wspornika były obarczone błędem ok. 200%.
3. W układach przesuwnych dokładność oszacowania sprawczych sił przekrojowych jest podobna do oszacowania przemieszczeń sprawczych.

 Fikcyjne obciążenia, równoważne imperfekcjom łukowym

Do wyznaczania obciążenia zastępczego dla danego wymuszenia stosuje się następujące kryteria sprawczego efektu:

• statyczne (S) – najczęściej przez porównanie momentu zginającego w przekroju sprawczym,
• przemieszczeniowe (P) – najczęściej w drodze porównania przemieszczenia przekroju sprawczego,
• energetyczne (E)– najczęściej przez porównanie energii odkształcenia postaciowego zgromadzonej w przekroju sprawczym, analogicznie do kryterium wytężeniowego H-M-H

Metoda energetyczna jest najdokładniejsza, ale zbyt złożona do obliczeń ręcznych – może być stosowana w obliczeniach komputerowych.

Obciążenie fikcyjne z kryterium statycznego

W normie Eurokod 3 do wyznaczenia fikcyjnego (zastępczego) obciążenia równoważnego imperfekcjom łukowym, zastosowano kryterium statyczne. Z porównanie momentu zginającego w przekroju sprawczym S pręta przegubowo-przegubowego (Rys.4-2.5b) wywołanych siła osiową $N$ (oznaczenie normowe $N_{Ed}$ ) na przemieszczeniu $e_L$ ( oznaczenie normowe $e_{0,d}$ ) i momentu zginającego wywołanego równomiernie rozłożonym, fikcyjnym obciążeniem $q_L$ (oznaczenie normowe $q_d$), czyli z warunku

$\left( M_S=\cfrac{q_L L^2}{8}\right) =(M_L=N\cdot e_L$),  uzyskano formułę  [6], (3.9) .

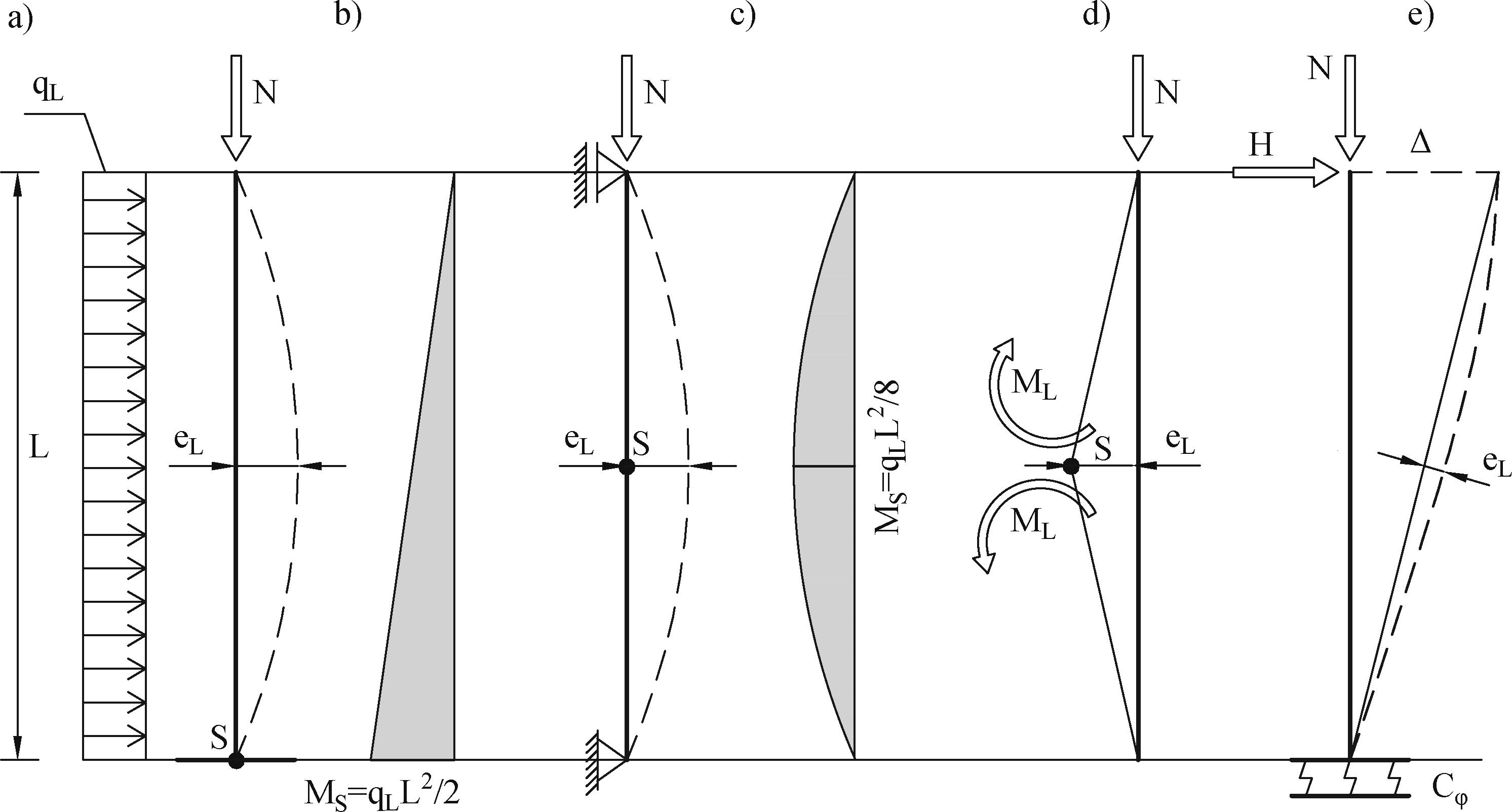
Rys.4-2.5. Analiza fikcyjnych obciążeń poprzecznych mimośrodu imperfekcji: a) obciążenie fikcyjnymi siłami poziomymi, b) pręt przegubowo-przegubowy, c) pręt wspornikowy, d) obciążenie fikcyjnymi momentami (opracowanie własne)

Pokażemy, że formuła normowa [6],(3.9) jest poprawna tylko dla pręta o schemacie przegubowo-przegubowy

Dla schematu statycznego wspornika (Rys.4-2.5c) przekrój sprawczy nie jest położony w środku wysokości. Rozważmy dwa położenia przekroju sprawczego:

• w utwierdzeniu $x_S=L$
  Moment zginający od obciążenia  $q_L$wynosi $M_S=q_L L^2/2$. W sytuacji, w której pręt zostanie tak zmontowany, że amplituda imperfekcji zostanie ułożona w wierzchołku, czyli $\Delta=e_L$, więc $M_L=N\cdot e_L$. Mamy stąd obciążenie fikcyjne $q_L=2\cdot N\cdot e_L/ L^2$, co jest czterokrotnie mniej od wynikającego z formuły normowej [6],(3.9) ,

• w miejscu maksymalnego wygięcia łukowego (strzałki wygięcia) $x_S=x_{max}$
  Obciążenie fikcyjne $q_L$ powoduje wychylenie  wspornika w pełni utwierdzonego w podstawie ( $C_\varphi =\infty $ ) o $\Delta=\cfrac{q_L L^4}{ 8EI }$. Strzałka wygięcia wystąpi w odległości  $ x_{max}=L / \sqrt[3]{4} = 0.63 L$ od wierzchołka. Moment zginający w tym miejscu wynosi $M_{S2}= \cfrac{q_L L^2}{2}=\cfrac {q_L L^2 } {2 \sqrt[3] {16}} = \cfrac{5,04 \cdot q_L}{L^2}$. Z warunku $M_S=M_L=N\cdot e_L$, otrzymujemy $q_L= \cfrac {5,04 N\cdot e_L}{l^2}$ , czyli o ponad 50% mniejsze od wynikającego z formuły normowej [6],(3.9) .

W przypadku wspornika często imperfekcję łukową zastępuje się przyłożeniem do głowicy słupa siły N na mimośrodzie $e_L$, to znaczy dodatkowe obciążenie głowicy momentem (tak przyjęto na przykład w często przywoływanym przykładzie  [7] ). Wyżej, a także w przykładzie 6.1.2 (rozdział 6), pokazano, że takie podejście nie jest poprawne.

Wnioski:

1)  Wzór normowy [6],(3.9) na obciążenie fikcyjne dotyczy tylko pręta przegubowo-przegubowego

2)  Zastąpienie imperfekcji łukowej wspornika mimośrodem jet niepoprawne

Nowe propozycje wyznaczania rozłożonego obciążenie fikcyjnego

Obciążenie fikcyjne z kryterium plastycznego

W przypadku schematów innych niż przegubowo-przegubowy lepsze rezultaty uzyskuje się dla fikcyjnego obciążenia, parą momentów  $M_L$ przyłożonych po obu stronach przekroju sprawczego $S$ i wywołujące dodatkowy moment tylko w tym przekroju. Takie fikcyjne obciążenia stosowane na etapie obliczeń wstępnych i koncepcyjnych dobrze współgrają z proponowaną w tej pracy uogólniona metoda imperfekcyjną w której należy przeprowadzić analizę mechanizmu plastycznego. Para momentów  $M_L$ w granicznym stanie plastycznym dąży do wartości $M_{pl}= W_{pl} \cdot f_y$, co jest statycznym odpowiednikiem przegubu plastycznego konstrukcji stalowej, lub aluminiowej. W przypadku konstrukcji żelbetowych moment graniczny powinien być wyznaczony z warunku ograniczenia maksymalnych rys w betonie. Z warunku $M_S=M_pl$ otrzymamy oszacowania granicznego, fikcyjnego obciążenia poziomego, niezależnego od N:

$$\begin{equation} q_L= n_{pl} \cdot M_{pl}/ L^2 \label {4-2.1.}\end {equation}$$

gdzie mnożnik $n_{pl} zależy od schematu pręta i w ogólnym przypadku jest wynikiem granicznej analizy plastycznej [8] . a w przypadkach szczególnych wynosi:

$$\begin{equation}  n_{pl}=\begin {cases}
8 & \text {dla pręta przegubowo-przegubowego, i przegubowo-utwierdzonego} \\
2 & \text {dla pręta wspornikowego} \\
12 & \text {dla pręta utwierdzono-utwierdzonego} \\
\end{cases} \label{4-2.1a} \end {equation}$$

Obciążenie fikcyjne z kryterium przemieszczeniowego

Z porównania ugięcia przekroju krytycznego wywołanego obciążeniem $q_L$ z amplitudą imperfekcji $e_L$ lub  $n_L=\cfrac{e_L}{L}$, otrzymamy następującą formułę:

$$\begin{equation} q_L= \cfrac{k_s EI}{n_L \cdot L^3} =\cfrac{L}{n_L \cdot \overline f_q} \label{4-2.2} \end {equation}$$

gdzie:
$k_S$  mnożnik zależny od schematu statycznego elementu i położenia przekroju krytycznego:

$$\begin{equation}  k_s =\begin {cases}
32 \sqrt[3]{4}=50,8  & \text {dla wspornika} \\
384/5 = 76,8 & \text {dla pręta przegubowo-przegubowego (wahacza)} \\
185  & \text {dla pręta przegubowo-utwierdzonego} \\
384 & \text {dla pręta utwierdzono-utwierdzonego} \\
\end{cases} \label {4-2.2.a} \end {equation}$$

$overline f_q$  strzałka ugięcia elementu od jednostkowego (wirtulanego) obciążenia poprzecznego $\overline q_d=1$ , uzyskana z analizy I rzędu.
W praktyce zalecamy wyznaczenie $\overline f_q$ dla schematu słupa z uwzględnieniem podatności węzłów w miejscu potencjalnej oceny imperfekcji łukowej, (czyli zapewne w środku rozpiętości elementu) i następnie wyznaczenie zastępczego obciążenia  z formuły ($\ref{4-2.2}$).

Z  ($\ref{4-2.2}$) wynika, że różnica równoważnych obciążeń lokalnych dla różnych schematów elementów może być znaczna, mimo, że w podejściu przemieszczeniowym nie zależy ona od siły osiowej, działającej w pręcie.

Imperfekcje łukowe konstrukcji żelbetowych

Globalna imperfekcja przechyłowa (IG) wyrażana przechyłem nie uwzględnia imperfekcji lokalnych, objawiających się odchyleniami linii obojętnej przekrojów żelbetowych od osi pionowej. Odchylenia te są spowodowane m.in.: niedoskonałościami szalunku, odchyleniem lokalizacji powyginanych prętów zbrojeniowych, niedokładnym zagęszczeniem mieszanki betonowej oraz niejednorodnym warunkami dojrzewania betonu.

Takie lokalne imperfekcje są mierzone amplitudą wygięcia $n_e=e/l$ , gdzie $e$ – amplituda (strzałka wygięcia), $l$- długość elementu (lub ogólniej długość odniesienia).

Na podstawie dopuszczalnych tolerancji wykonawczych zestawionych w Tab. 2.2 należałoby przyjmować wartość charakterystyczną lokalnej imperfekcji słupa lub ściany $n_{L,k}=max \{ 300 ; \quad l/30 \, w \, mm\}$ , a wartość obliczeniową $n_{L,d=n_L,k} / \gamma_{Lc}$ . Zaleca się przyjmować współczynnik obciążeń jak dla obciążeń zmiennych $\gamma_{Lc}=1,5$, ale ze współczynnikiem kombinacyjnym $\psi=0,8$, to znaczy $\gamma_{Lc}=1,5 \cdot 0,8=1,2$, czyli obliczeniowe imperfekcje wyniosą

$$\begin{equation}  n_{L,d} = \{  \max{ \{ 300; \quad 1/30 \, w \, mm\} } /1,2 = \{  \max{ \{ 250; \quad l /36 \, w \, mm\} } \label {IŻ} \end {equation}$$

Formuła ($\ref{IŻ}$) może być stosowana do czasu opracowania  doświadczalnie potwierdzonych wytycznych. W dalszej części podręcznika zaprezentowano przykłady analizy konstrukcji żelbetowych , obarczonych imperfekcjami łukowymi wyznaczonymi z  ($\ref{IŻ}$).

⇒ [następne] [ Proces stochastyczny imperfekcji systemowych ]

Niniejszy artykuł jest  częścią 2 rozdziału 4 podręcznika Imperfekcyjna metoda projektowania konstrukcji

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Historia edycji:
(2019-05, 30 Wersja 1.0 

 Literatura

1. PEER/ATC, (2010), Modelling and acceptance criteria for seismic design and analy-sis of tall buildings (PEER/ATC Report No. 72–1). Applied Technology Council
2. Powell G. H. (2010), Modelling for Structural Analysis. Behaviour and Basics. Com-puters and Structures, Inc
3. Consteel Software, (2019), ConSteel 13 Manual, [ https://consteelsoftware.com/downloads/ ]
4. Computer and Structures Inc. (2019). SAP2000. Structural Software for Analysis and Design (Version 21),. [ https://www.csiamerica.com/products/sap2000 ]
5. PN-EN 1993-1-8 +Ap1+AC:2006, Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
6. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
7. Arcelor-Mittal, (2009), Jednokondygnacyjne konstrukcje stalowe, Część 6: Projekt wykonawczy słupów złożonych. http://sections.arcelormittal.com/fileadmin/redaction/4-Library/4-SBE/PL/SSB06_Projekt_wykonawczy_slupow_zlozonych.pdf
8. Chodor L. (2016). Nośność plastyczna konstrukcji, Encyklopedia Inżyniera i Architek-ta πPiWiki, [ https://chodor-projekt.net/encyclopedia/nosnosc-plastyczna-konstrukcji/ ]

________________________________