Uwaga: artykuł jest w trakcie edycji . Zawiera treści tymczasowe.  

Niniejszy artykuł jest rozdziałem 5-1 podręcznika Imperfekcyjna metoda projektowania konstrukcji [ ← spis treści]
Nawigacja: [Uogólniona imperfekcja alternatywna] ⇐  ⊗  ⇒ [ Imperfekcje]

Artykuł w ciągu ostatnich 24 godzin czytało 0 Czytelników

Zaprezentowano  pojęcie uogólnionej, alternatywnej imperfekcji, będącej alternatywą klasycznej, sprężystej imperfekcji alternatywnej, to jest przeskalowanej  postaci wyboczenia sprężystego. Przedstawiono też pojęcie imperfekcji plastycznej.

Przykłady w tym rozdziale są przedstawiane dla obliczeniowych obciążeń zewnętrznych, wyznaczonych z formuły kombinacyjnej z redukcją obciążeń stałych, oraz przy jednym wiodącym obciążeniem zmiennym. W przykładach pomijano mnożnik ciężaru własnego. Czytelnik w samodzielnym ćwiczeniu może przeliczyć przykłady z ciężarem własnym (współczynnik obliczeniowy dla ciężaru własnego elementu należy przyjąć $\gamma_f=1,35\cdot 0.85=1,15$ .

Analiza przypadków obejmuje reprezentatywne rodzaje konstrukcji bez specjalnego rozróżniania typu materiału, co jest zgodne z praktyką projektową, w której projektant jednocześnie zajmuje się rozmaitymi rodzajami materiałów konstrukcji stalowo- betonowo aluminiowej.

Przedstawione w 1-szej części rozdziału 5 przykłady rachunkowe dotyczą najprostszych przypadków pręta prostego jednogałęziowego. W kolejnych częściach przedstawimy przykłady coraz bardziej złożonych konstrukcji.

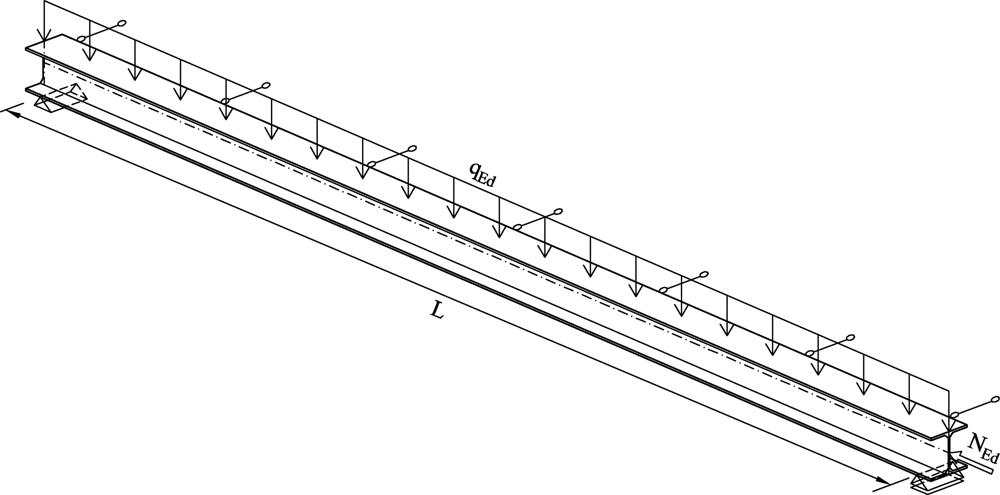
Przykład 5-1.1. Ściskana belka stalowa bocznie stężona

Swobodnie podparta belka stalowa o długości L=5,4m  (Rys. 5-1.1), wykonana jest z dwuteownika HEA 200-S235. Charakterystyki HEA 200:   $A= 53,80 \, cm^2$, $g=0,42\, kN/m$, $I_y=3690m \, cm^4$, $i_y=8,28 \, cm$, $W_{pl,y}=429,5 cm^3$, $I_z=1336 \, cm^4$, $i_z = 4,98 \, cm$, $W_{pl,z}=203,8 \, cm^4$. Pas górny belki jest zabezpieczony przed bocznym wyboczeniem (zwichrzeniem), a belka-słup przed wyboczeniem giętnym z płaszczyzny.

Rys. 5-1.1. Belka-słup stalowy do przykładu 5.1.

Miarodajne siły przekrojowe 1 rzędu wystąpią w przekroju krytycznym w środku długości elementu: $N_{Ed}=600 \, kN$  $M_{Ed}=\cfrac{9,42 \cdot 6,42}{8}=34,34 \, kNm$.

Wytężenie elementu metodą klasyczną HWEM

Smukłość pręta wyznaczona z (1-1.8) wynosi.

$\overline \lambda=\cfrac{540}{8,28}\cdot \cfrac{1}{93,9 \cdot 1}=0,695$.

Dla krzywej wyboczeniowej „b” (wyboczenie względem osi y) parametr imperfekcji wynosi  $\alpha=0,34$  – Tab.1-3.2 (

PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków

, tab.6.2 ).

Współczynnik pomocniczy  (1-4.4) $\Phi=0,5 \cdot [1+0,34\cdot (0,695-0,2)-0,695^2]=0,825$,
współczynnik wyboczeniowy (1-4.3)  $\chi=\cfrac{1}{0,825+\sqrt{0,825^2 -0,695^2}}=0,787$.

Nośność elementu na ściskanie  $N_{bRd}=0,787\cdot 1264,3/1,0=995,0 \, kN$

Nośność belki na zginanie ($\chi_{LT}=1,0$ ) $M_{bRd}= 1,0\cdot 100,9=100,9 \, kNm$

Wytężenie belki- słupa wyznaczone klasyczną, już historyczną metodą HWEM wynosi:

$w^{HWEM}=\cfrac{600,0}{995,0 /1,0}+\cfrac{34,34}{100,9/1,0}=0,603+0,340=0,934$\

Imperfekcja przechyłowe

W rozpatrywanym elementarnym przypadku statycznie wyznaczalnym, przemieszczenia węzłów elementu (podpór), wynikające z imperfekcji przechyłowych nie skutkują zmianą w wytężenia elementu. Odgrywa rolę natomiast niezamierzony mimośród przyłożenia siły ściskającej do czoła elementu.

W klauzuli [1], kl. 5.3.1(1) nałożono obowiązek uwzględniania niezmierzonych mimośrodów montażowych, ale nie podano wytycznych do przyjmowania ich wartości. Wobec tego możliwe mimośrody wytwarzania i montażu należy wyznaczać indywidualnie po przeanalizowaniu technologii montażu i ograniczeń konstrukcyjno-technologicznych. Dopuszczalne odchyłki przyjęte w projekcie, należy ujawnić Wykonawcy w specyfikacji technicznej wykonania i odbioru konstrukcji.

Niezamierzony mimośród przyłożenia siły ściskającej do czoła słupa wyznaczamy z formuły, analogicznej w zapisie do formuły zalecanej w projektowaniu konstrukcji żelbetowych [1],kl. 5.3.1(1) :

$$\begin {equation} e_G= max \{ \cfrac{h}{50} \, ; \, 5 \, mm \} \label{5-1.1} \end {equation}$$

gdzie uwzględniono zapisy normy [2] , w której określono, że przesunięcie blachy podstawy słupa względem osi słupa nie powinno przekraczać $e=5\,mm$ dla klasy 1 wytwarzania, a wysokość kształtownika spawanego może mieć odchylenie nie większe niż  $e=h/50$.

W rozważanym przypadku mamy
$e_G= max \{ \cfrac{190}{50} \, ; \, 5 \, mm \}= 5 \, mm$.

Mimośrodowe, niezamierzone przyłożenie obciążenia pionowego do pasa górnego, wyznaczono z formuły

$$\begin {equation} e_{G,e}= max \{ \cfrac{b}{100} \,; ], t_w \, ; \, 3 \, mm \} \label{5-1.2} \end {equation}$$

W rozważanym przypadku mamy $e_{G,e}= max \{ \cfrac{200}{100} \,; ], 6,5 \, ; \, 3 \, mm \}$ jest odsunięciem płaszczyzny obciążenia od płaszczyzny głównej zginania belki. Ze względu na zabezpieczenie boczne belki w przykładzie nie jest sprawcze i nie będzie dalej analizowane. To samo dotyczy równoważnych obciążeń poziomych , pochodzących od ciężaru belki.

Imperfekcje łukowe

Imperfekcja łukowa ma amplitudę jak dla krzywej „b” wg Tab. 3-2.1  $n_L=250$ ($e_L=5400/250=6,7 \, mm$

Amplituda imperfekcji – sposób alternatywny AIM

Zintegrowaną amplitudę imperfekcji wyznaczono sposobem alternatywnym AIM (pkt. 3.6) za pomocą kalkulatora programu Consteel. Przeprowadzono analizę wyboczeniową (LBA) pod obciążeniami siłą pionową V i ciężarem własnym g. W wyniku uzyskano dwie postacie wyboczenia. Dla pierwszej postaci ywboczenia formuły (3.10) dla uzyskano

Historia edycji:
(2019-05, 30 Wersja 1.0 
[2019-06-15] Naprawienie błedu portalu

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Proszę społeczność Inżynierów w internecie o przesyłanie recenzji podręcznika  na adres  wydawnictwa biuro@chodor-projekt.net
Leszek Chodor

 Literatura

1. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
2. PN-EN 1090-2+A1:2012, Wykonanie konstrukcji stalowych i aluminiowych , Część 2: Wymagania techniczne dotyczące konstrukcji stalowych

________________________________