Artykuł w ciągu ostatnich 24 godzin czytało 29 Czytelników
Uwagi i recenzje podręcznika przesyłać na adres wydawnictwa: wydawnictwo@chodor-projekt.net lub leszek.chodor@chodor-pojekt.pl
spis treści prodręcznika: [ Imperfekcyjna metoda projektowania konstrukcji ]
Część 2-2
Nawigacja: [ 2-1: Imperfekcje i ich źródła] ⇐ ⊗ ⇒ [ 2-3: Geneza metod imperfekcyjnych]
W konsekwencji tego, że tolerancje wykonawcze wraz ze sposobem ich kontroli i odbioru elementów są określone w projekcie, jest to, że również wartości geometrycznych imperfekcji projektowych powinny być przyjęte przez Projektanta na podstawie wyspecyfikowanych tolerancji wykonawczych oraz metodologii statystycznej kontroli tych tolerancji. Prawidłowy opis wymagań dotyczących statystycznej kontroli jakości i odbioru konstrukcji jest ważnym elementem projektu, który w istocie decyduje o wartościach geometrycznych imperfekcji systemowych.
Niniejszy artykuł jest poświęcony wyznaczaniu imperfekcji projektowych ze znanych odchyłek wykonawczych i sposobu ich statystycznej kontroli podczas odbioru konstrukcji.
Tolerancje wykonawcze źródłem imperfekcji i kosztów
Koszty wykonania konstrukcji a odchyłki wykonawcze
Tolerancje ustanowione w przepisach dotyczą odchyłek, wymagających normalnej staranności od Wykonawcy. Jeśli potrzebne są większe wymagania, to odpowiednie zalecenia powinny być przedstawione w specyfikacji wykonania i odbioru, opracowanej przez Projektanta. Należy zwrócić uwagę, że nadmierne zwiększenie wymagań nie jest ekonomicznie uzasadnione, bowiem zwykle prowadzi do nieproporcjonalnego zwiększenia kosztów. Na rys. 2.4 pokazano przyrost kosztu budowy wygenerowany koniecznością dotrzymania tolerancji $\Delta$ [mm] konstrukcji żelbetowej budynku na długości bazy L [m] . Bazę można interpretować, jako wysokość budynku, a tolerancję Δ jako dopuszczalne odchylenie od pionu przed obciążeniem. Dla porównania zgodnie z [1] normalne tolerancje dla bazy L [m] w konstrukcji określono na $\Delta= \pm 4 \sqrt{L} \,mm$.
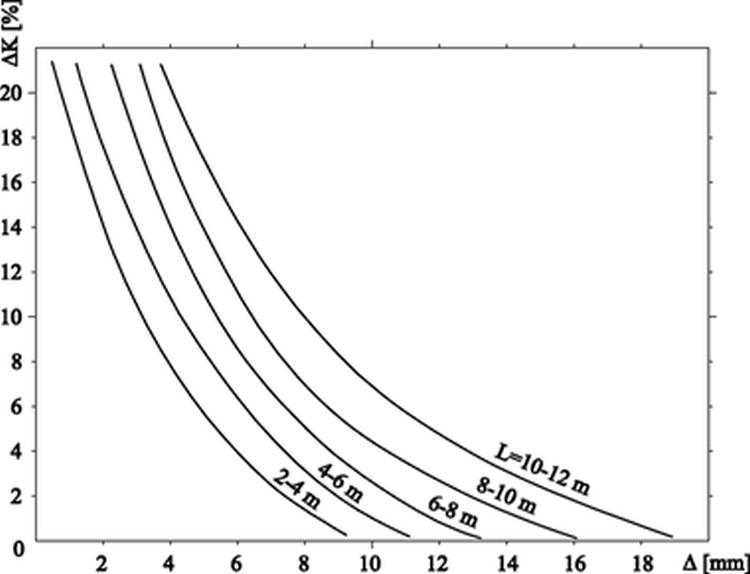
Rys. 2-2.1 Koszty zmniejszenia tolerancji wychyleń budynku (opracowano na podstawie [2] )
Z rys. 2-2.2 wynika, że konstrukcje budowlane są naprawialne, więc w celu ustalenia optymalnych wartości tolerancji należy wziąć pod uwagę nie tylko koszty inwestycyjne $\Delta K_I$ zwiększenia jakości budowli poprzez zawężenie tolerancji jej wykonania, ale również koszty awarii $\Delta K_A$ związanych z postojami, serwisem, utrzymywaniem gotowości gwarancyjnej, a także kosztami konsekwencji awarii (w tym życia i zdrowia użytkowników obiektu). Wyznaczenie punktu optimum niezawodności $R_{opt}$ systemu z warunku sumarycznych kosztów inwestycyjnych $\Delta K_I \approx \Delta K_R$ oraz eksploatacji $\Delta K_N$ jest możliwe w drodze pogłębionej analizy systemu konstrukcyjnego w całym okresie jego życia. Krytyczne wartości niezawodności $R_{cr}$ wynikają z wymogów bezwzględnych: $R_{cr}’$ – minimalna wartość niezawodności, akceptowana społecznie, najczęściej wpisana do norm: $R_{cr}”$ – maksymalna wartość niezawodności wykraczająca poza potrzeby społeczności, regionu i państwa , wynikająca z polityki gospodarczej i społecznej.
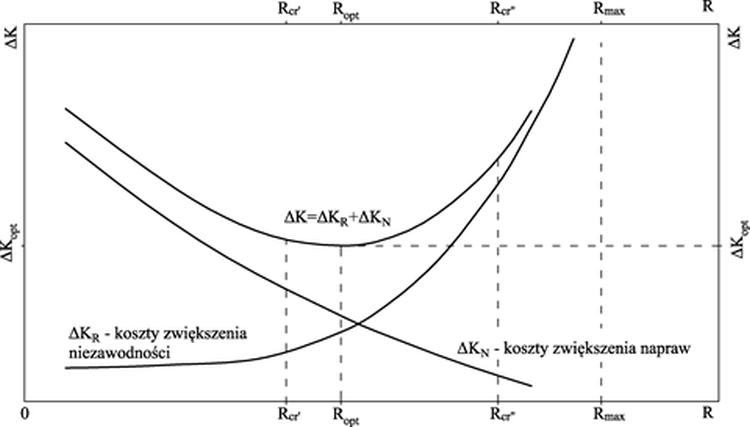
Rys. 2-2.2 Koszty zwiększenia niezawodności R konstrukcji (opracowano na podstawie [3] )
Od obiektów budowlanych wymaga się jednocześnie dużej niezawodności i dużej trwałości. Trwałość jest podstawową miarą jakości obiektu. Jakość obiektu jest większa, jeśli przez dłuższy okres zachowuje założone właściwości. Korelacja pomiędzy projektowym okresem użytkowania T , zdefiniowanym w [4] , a trwałością obiektu $R_T$ mierzoną w latach jest dodatnia , to znaczy trwałość obiektu rośnie wraz ze zwiększaniem $T_R$. Na przykład średnia trwałość budynków wiejskich (rolniczych) wynosi $T_R= 70 \, lat$ [3] , a projektowy okres użytkowania (okres powrotu dla obciążeń okresowo zmiennych) wynosi $T_P$ 15 do 30 lat [4] , a średnia trwałość kamienic mieszkalnych wynosi $T_R \approx 100 \, lat$ podczas , gdy $T_P = 50 \, lat$.
Dodatnia korelacja zachodzi również pomiędzy niezawodnością $R=1-p_f$, a trwałością, gdzie $f_p$ jest prawdopodobieństwem awarii (nie zachowania wymaganych właściwości) w okresie eksploatacji $t_p$. Generalnie konstrukcje budowlane są wieloelementowymi oraz wielokryterialnymi, monotonicznymi systemami z punktu widzenia niezawodności (p. również Dodatek C).
Inżynierowie, a w ślad za ich potrzebami również przepisy normowe zamierzają do zdefiniowania imperfekcji dla wydzielonych elementów konstrukcyjnych (przede wszystkim słupów i prętów).
Korelacja imperfekcji z tolerancjami na przykładzie konstrukcji żelbetowych
Dopuszczalne tolerancje konstrukcji, są odwzorowane na wartości imperfekcji projektowych. Ścisłą korelację zauważono w komentarzu [5] do PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków, co przedstawiono na rys. 2-2.3. Porównano projektowe imperfekcje przechyłowe zalecane przez [6], z tolerancjami konstrukcji żelbetowych w 1 klasie wykonania (samokontrola lub inspekcja z procedurami jednostki bez specjalnych procedur odbiorczych). Przyjęto, że wartość podstawowej imperfekcji pochylenia wynosi 1/300 wyznaczono jako średnią z 1/200 dla konstrukcji wrażliwych i 1/400 dla niewrażliwych na efekty drugiego rzędu). Z porównania wynika, że istnieje ścisła korelacja tolerancji wykonania z imperfekcjami projektowymi.
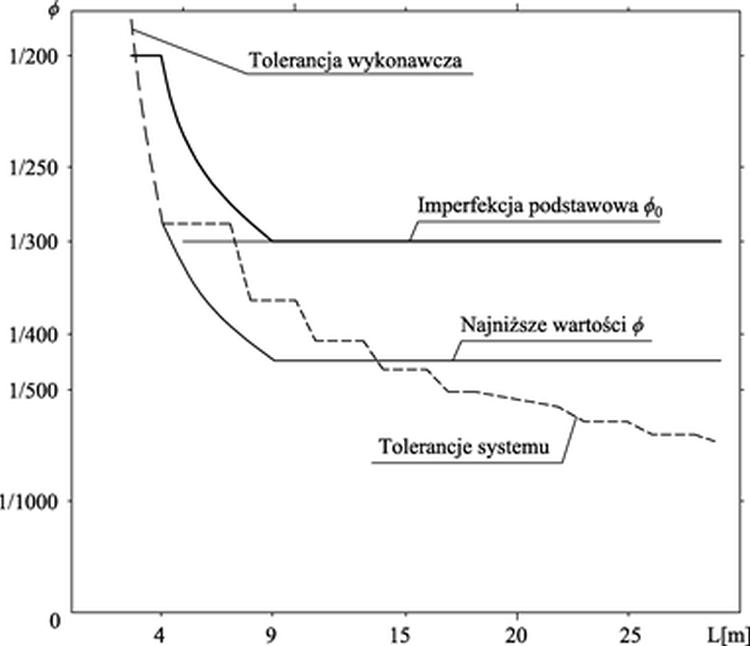
Rys. 2-2.3. Porównanie imperfekcji przechyłowych wg 5.1. EC2 i tolerancji konstrukcji żelbetowych wg PN-EN 13670 . Tolerancje naniesione linią ciągłą dotyczą słupa kondygnacji, a linią przerywaną całkowitego wychylenia konstrukcji (opracowano na podstawie[5] )
Z analizy zestawień w Tab. 2.1 do Tab. 2.4 wynika, że dopuszczalne tolerancje konstrukcji, są odwzorowane na wartości imperfekcji projektowych wg formuły:
$$\begin{equation} n_P= \cfrac{n_w}{\gamma_i} \label{2-2.1} \end {equation}$$
gdzie wprowadzono pojęcie częściowego współczynnika bezpieczeństwa dla imperfekcji $\gamma_i>1$, który został oszacowany w kolejnym rozdziale. Przy braku wystarczających danych, bez szczególnych zaleceń odnośnie wykonania i odbioru budowli, można przyjąć $\gamma_i \approx 2$.
Po przyjęciu właśnie takiej wartości współczynnika częściowego dla imperfekcji, otrzymano formuły na imperfekcje projektowe zamieszczone w kol. (7) Tab. 2.1, Tab. 2.2 oraz kol. (4) Tab. 2-2.1 Oszacowane wartości imperfekcji projektowych umożliwiają analizę szeregu przypadków konstrukcji z imperfekcjami, dla których w normach nie podano zalecanych wartości, a także umożliwiają rozróżnianie imperfekcji dla poszczególnych typów konstrukcji, dla których definiowane inne dopuszczalne tolerancje.
W większości sytuacji utrzymanie normalnych tolerancji jest wystarczające. Jednakże często ze względów konieczności prawidłowego pasowania części budynku tolerancje należy zaostrzyć. Jak pokazaliśmy zaostrzenie wymogów tolerancji wykonawczych prowadzi również do zmniejszenia imperfekcji projektowych, a w konsekwencji do wykonania projektu budynku o mniejszej materiałochłonności. W rezultacie teoretycznie możemy osiągnąć oszczędności materiałowe kosztem zwiększenia wymogów wykonawczych. W tym kontekście imperfekcje projektowe zalecane w normach projektowania nie są bezwzględne i mogą być świadomie ulepszone przez Projektanta w
porozumieniu z Inwestorem zgodnie z koncepcją, przedstawioną w kolejnym punkcie.
Koncepcja współczynnika imperfekcji
Kontrola jakości konstrukcji i jej zgodności z tolerancjami wykonawczymi prowadzona jest w ramach samokontroli i kontroli służbami Wykonawcy, a ostatecznie przez nadzór budowlany, reprezentowany przez inspektora nadzoru inwestorskiego oraz ewentualnie inspektora nadzoru projektowego.
Podczas odbioru konstrukcji nadzór budowlany dokonuje ciągu pomiarów imperfekcji (odchyłki od wartości nominalnej) $\Delta$ oraz bazy pomiarowej L . Liczebność tych pomiarów zwykle nie jest duża i nie przekracza kilku. W zależności od sposobu wyrażenia dopuszczalnej tolerancji:
$\Delta_{lim}$, lub $(n_{\Delta})_{lim}=(\tfrac{\Delta}{L})_{lim}$.
zostaje wyznaczona stosowna statystyka z pomiarów. Załóżmy, że zgodnie z przyjętym w tej pracy założeniem ($\ref{2-2.1}$) oraz sposobem przedstawienia dopuszczalnych tolerancji przyjętym w Tab. 2.1 do Tab. 2.4 poprzez określenie dopuszczalnej wartości imperfekcji $(n_{\Delta})_{lim}$.
W tym przypadku wielkości pomiarowe (i=1..n) można ułożyć w szereg od wartości najmniejszej do największej: . Statystyką $m_{n_\Delta}$ pomiarów jest średnią z pomiarów
$$ \begin {equation} m_{n_\Delta} = \cfrac{1}{n}\sum \limits_{i=1}^n n_{\Delta_i} \label{2-2.2} \end{equation}$$
lub minimum z pomiarów
$$ \begin {equation} m_{n_\Delta} = \max \limits_{i=1}^n {n_{\Delta_i}} \label{2-2.3} \end{equation}$$
Ocena statystyki odchyłki $m_{n \Delta}$ jest obarczona niepewnością związaną z małą liczebnością próby, a także zależną od metodyki odbioru i dokładności pomiaru, od kategorii nadzoru budowlanego, a także od innych czynników takich jak błędy ludzkie, kategoria użytkowania konstrukcji oraz zdarzeń wyjątkowych. Nie są znane inne parametry losowe populacji, z której pochodzi próba. W szczególności nie jest znany współczynnik zmienności $V_{n\Delta}$ nawet, jeśli zostanie estymowany z doraźnej próby. Analizę wyznaczenia imperfekcji projektowej z tolerancji wykonawczej należy prowadzić dla nieznanej wartości $V_{n\Delta}$.
W projektowaniu należy przyjmować wartości charakterystyczne cechy obiektu, które należy wyznaczać tak, by reprezentowały 5% kwantyl przy nieskończonej liczbie prób.
Taka odpowiedniość dla cechy X rozłożonej normalnie opisana jest zasadą normową dla sytuacji projektowania wspomaganego badaniami [4],kl. D7.2(1) :
$$\begin {equation} X_{k(n)}= m_X\cdot (1-k_n V_X) \label{2-2.4} \end {equation}$$
gdzie:
$X_{k(n)}$ – wartość charakterystyczna cechy $X$ , stanowiąca kwantyl wyznaczony na podstawie pomiarów o liczebności n. Wartość średnia z próby i współczynnik zmienności populacji jest estymowany z losowo pobranej próby n-elementów i za pomocą współczynnika tolerancji zależnego od liczebności próby. Estymatorem średniej jest średnia arytmetyczna, a w sytuacji małej liczebności pomiarów współczynnik $V_X$ nie jest znany.
Przyjmujemy zasadę, że imperfekcje projektowe $n_p$ można oszacować z tolerancji wykonawczych $n_w$ z formuły ($\ref{2-2.1}$) , a współczynnik imperfekcji, $\gamma_i$ wyznaczymy dla dwóch statystyk ($\ref{2-2.2}$) i ($\ref{2-2.3}$).
Przy założeniu, że zmienna X i Y są zmiennymi losowymi o rozkładach normalnych $N(m_X, \sigma_X)$ i $N(m_Y, \sigma_Y)$ odpowiednio i o współczynniku korelacji $\rho_{XY}$, to ich iloraz X/Y jest zmienną losową o rozkładzie Cauchyego [7] , dla której w ogólności nie istnieją momenty statystyczne. Dokonamy aproksymacji rozkładu X/Y zgodnie z wynikami pracy [8] , gdzie pokazano, że jeśli Y może przyjmować tylko wartości dodatnie, to iloraz X/Y ma rozkład w przybliżeniu normalny z dystrybuantą:
$$\begin {equation} F_{XY}(t)= Pr (x/y <t) = \Phi \left \{ \cfrac{t \cdot m_Y- m_X}{\sqrt{\sigma_X^2 – 2\cdot t \cdot \rho_{XY} \cdot \sigma_X \cdot \sigma_Y + (t \cdot \sigma _Y)^2}}\right \} \label{2-2-2.2} \end {equation}$$
Jeśli założymy, że $n_w$ i $n_p$ ($\ref{2-2.1}$) są nieskorelowane i mają takie same współczynniki zmienności $\sigma_{n_p} / m_{n_p}=\sigma_{n_w} / m_{n_w}=V_{n_\Delta}$ , oraz średnie $m_{n_p}=m_{n_w}= m_{n \Delta}$ to z ($ \ref {2-2-2.2}$) otrzymamy
$$\begin {equation} F_{ \gamma_i} (t) = Pr ( \gamma_i<t) = \Phi \left \{ \cfrac { t m_{n_p} – m_{n_w} } { V_{n \Delta} \cdot \sqrt{ m_{n_w}^2 + (t m_{n_p})^2} } \right \} =\Phi \left \{ \cfrac{t-1}{V_{n \Delta} \cdot \sqrt{1+t^2} } \right\} \label{2-2.6}\end {equation}$$
Z równania $F_{\gamma_i}(t)=\alpha$ można wyznaczyć wartość charakterystyczną współczynnika imperfekcji jako kwantyl na poziomie $\alpha$. Kwantyl 5% standaryzowanego rozkładu normalnego wynosi 1,64.
Imperfekcja projektowa w sytuacji oceny wartości średniej
W przypadku oceny średniej $m_{n \Delta}$ odchyłki $n_{\Delta}$ ,współczynnik tolerancji $V_{\Delta}$ w formule ($\ref{2-2.6}$) można odczytać z [4]– tab D.1 . Przy nieznanym współczynniku $V_{ \Delta} $ mamy:
$$ \begin {equation} k_n = \begin {cases}
3,37 & \text {dla n=3} \\
1,64 & \text {dla n $\to \infty$ } \\
\end {cases} \label {2-2.7} \end {equation}$$
Powyższe wnioskowanie i wartości współczynników tolerancji ($\ref{2-2.7}$) są związane z rozkładem t-Studenta na $s=n-1$ stopniach swobody, który dla $n \to \infty$ zmierza do rozkładu normalnego.
Stosunek $\gamma_i$ wartości $n_{\Delta_k}$ estymowanej z próby o ograniczonej liczebności (dla $k_n= 3,37$ ) do wartości projektowej (dla $k_n=1,64 $ ) wynosi:
$$\begin {equation} \gamma_i=\cfrac{1/V_{n \Delta}- 3,37}{1/V_{n \Delta}- 1,64} \label {2-2.8} \end {equation}$$
i ma dwie charakterystyczne granice:
$$ \begin {equation} \lim { \, \gamma_i} = \begin {cases}
1 & \text {dla n $\to 0$ } \\
\sim 2 & \text {dla n $\to \infty$ }
\end {cases} \label {2-2.9} \end {equation}$$
Granica $\gamma_i=1$ jest trywialna, bowiem dotyczy sytuacji deterministycznej, przy czym taka granica jest lokalna, a krzywa posiada asymptotę globalną $ \gamma_i = \infty $.. Dla wartości średniej można więc przyjąć:
$$\begin {equation} \gamma_i\approx 2,0 \label{2-2.10} \end {equation}$$
Oznacza to, że w projektowaniu należy rozpatrywać sytuację 2-krotnie gorszą od wynikającej z dopuszczalnych tolerancji wykonawczych. Z zaprezentowanej idei wynika, że zaostrzenie procedur odbioru konstrukcji, lub (w mniejszym stopniu) zawężenie tolerancji wykonawczych prowadzi do łagodniejszego współczynnika imperfekcji ($\ref{2-2.8}$). Przykładowo przy zwiększeniu liczebności pomiarów do n=5 wskaźnik tolerancji rozkładu t-Studenta wynosi $t_4=2,776$ i współczynnik imperfekcji wyniesie $\gamma_i =1,7$
Imperfekcja projektowa w sytuacji oceny wartości ekstremalnej
W przypadku oceny ekstremalnej odchyłki n m (2.4) kwantyl statystyki wyznacza się z innej niż ($\ref{2-2.4}$) formuły. Ponieważ liczebność n statystyki porządkowej jest mała, więc zastosowanie asymptotycznych rozkładów wartości ekstremalnych z Dodatku A nie będzie odpowiednie.
Struktura typu „minimum” jest systemem szeregowym z punktu widzenia niezawodności, więc zachodzi zasada iloczynu niezawodności, który dla losowo niezależnych pomiarów można zapisać w postaci [3] :
$$\begin {equation} p_R= \prod \limits _{i=1} ^n p_{Ri} \label{2-2.11} \end {equation}$$
gdzie prawdopodobieństwo sukcesu (niezawodność) wynosi $p_{R_i}= Pr \{ n_{\Delta_i } > n_{\Delta_{dop}} \} $
Dystrybuanta zmiennej ($\ref{2-2.4}$) wynosi więc
$$\begin {equation}F_i (n_{\Delta} )=1- \prod \left [ 1-F_i (n_{\Delta} ) \right ] \label{2-2.12} \end {equation}$$
Kwantyl na poziomie $\alpha$ można wyznaczyć z równania
$$\begin {equation} n_{\Delta_k} =F^{-1} (1-\alpha) \label{2-2.13} \end {equation}$$
Na przykład dla trzech pomiarów n=3 i przy poziomie wiarygodności (dokładności) każdego pomiaru 95%, mamy $ \alpha=1-0,95^3=0,86$
Współczynnik imperfekcji w sytuacji kilku kryteriów tolerancji
W przypadku kilku kryteriów na imperfekcję określonego rodzaju wynikających z różnych warunków, na przykład dla imperfekcji przechyłowej $n_\Phi$ z warunków: tolerancji wykonawczej przechyłu słupa jednej kondygnacji $n_{w,1}$ oraz z warunku tolerancji przechyłu budynku wielokondygnacyjnego $n_{w,2}$ , a także różnych warunków zaleconych w normach do projektowania – dla danego typu konstrukcji lub dla typów, pozostających na styku zaprojektowanego układu (np. ramy stalowo-betonowej) $n_{p,1}$ i $n_{p,2}$ najczęściej wybiera się warunek najostrzejszy i on stanowi podstawę do odbioru konstrukcji. Typowym przypadkiem jest powszechnie przyjmowane założenie, że imperfekcja przechyłowa słupów kondygnacji i całego budynku zachodzi zgodnie w tym samym kierunku, a jako kryterium odbioru wybiera się ostrzejszy z warunków dla całego budynku lub dla słupa jednej kondygnacji.
Ocena wartości ekstremalnej ($\ref{2-2.4}$) rozbuduje się w ten sposób, że będzie zawierało zmieszane warunki cząstkowe.
Przykłady
Na przykładzie budynku żelbetowego oraz stalowego słupa dwugałęziowego zilustrowano sposób wyznaczenia imperfekcji projektowych z imperfekcji wykonawczych. Porównanie wyznaczonych imperfekcji z zaleceniami norm projektowania zamieszczono w dalszej części pracy. W przykładach nie zajmowano się współczynnikami redukcyjnymi, związanymi ze statystycznym efektem skali oraz probabilistyczną jednoczesnością imperfekcji.
Przykład 2-2.1 Imperfekcje projektowe z tolerancji konstrukcji żelbetowej
Dla budynku żelbetowego pokazanego na Rys. 3-7.5, na podstawie tolerancji wykonawczych ustalić projektową imperfekcję przechyłową UPI, łukową EŁI oraz UŁI, a także niezamierzony mimośród UEI.
Tab 2-2.1. Przykład wyznaczania imperfekcji projektowych z tolerancji konstrukcji żelbetowej
| Rodzaj imperfekcji i wyliczenia | Odniesienie w podręczniku1) |
| Dane :
Wysokość budynku $H=33 \, m$, |
($\ref{2-2.10}$) |
| Imperfekcje przechyłowe UPI $n_{\Phi} =\cfrac{1}{\Phi}$:
kondygnacji L=h= 3000 mm $\to n_{\Phi} =\min{ \{ 3000/15 \, ; \, 400\}}= \min{\{ 200 \, ; \, 400\}}=200$, Imperfekcje projektowe z tolerancji wykonawczych: |
tab.. 2-1.2 :
wrs 1, ($\ref{2-2.1}$) |
| Imperfekcje łukowe układu UŁI $n_{EŁ}=H/e$
Bazę wygięcia przyjęto jako dopuszczalne odchylenie od pionu w połowie wysokości budynku $L= H/2=33/2= 16,45 \, m$, $n=11/2=5,5$ $n_{S,L}= \max {\{ 16500/50 \, ; \, 200 \sqrt{(5,5)} \}}= \max{\{ 330 \, ; \, 469\}}=469$, Imperfekcje projektowe z tolerancji wykonawczych: |
tab.. 2-1.2 :
wrs 2 ($\ref{2-2.1}$) |
| Imperfekcje łukowe elementu EŁI
$ n_{L,\Phi} = \max{\{ 3000/30 \, ;\, \min{ \{ 3000/15 \,;\, 300\}}\}}=\max{\{ 100 \,;\, \min{\} 200 \,;\, 300\}}\}}=200$ Imperfekcje projektowe z tolerancji wykonawczych: |
tab. 2-1.2:
wrs 6 ($\ref{2-2.1}$) |
| Mimośród niezamierzony elementu EŁI
bok słupa b=(500+500)/2= 500 mm mimośród słupa mimośród belki $ n_{w,N}= \pm \min { \{ 500/20 \, ; \, 30\}} = \pm 25,0 $ mimośród łożyska mimośród niezamierzony: |
tab. 2-1.2:
wrs. 3, wrs. 4, wrs. 5 ($\ref{2-2.1}$) |
| 1) wrs jest odniesieniem do kol 5 w tab . 2-1.2 | |
Imperfekcje projektowe ustalane zgodnie z normą do projektowania konstrukcji żelbetowych [9] wyznaczono miedzy innymi w przykładzie 3-3.1.
Przykład 2-2.2 Imperfekcje projektowe z tolerancji konstrukcji stalowej
Dla hali stalowej, pokazanej na Rys. 3-7.4, na podstawie tolerancji wykonawczych ustalić projektową imperfekcję przechyłową UPI oraz łukową EŁI.
Tab. 2-2.2. Przykład wyznaczenia imperfekcji projektowych z tolerancji wykonawczych konstrukcji stalowej
| Rodzaj imperfekcji i wyliczenia | Odniesienie w książce1) |
| Dane : (kierunek x po długości hali; y – w płaszczyźnie układu poprzecznego)
długość hali $L_x= 40 \, m$, |
($\ref{2-2.10}$) |
| Imperfekcje przechyłowe UPI $n_\Phi =\cfrac{1}{\Phi}$:
w kierunku x $n_{px}=300$, Imperfekcje projektowe z tolerancji wykonawczych: |
tab.. 2-1.1 :
wrs 1, ($\ref{2-2.1}$) |
)Imperfekcje łukowe elementu EŁI
|
tab.. 2-1.1 :
wrs 6 |
| 1) wrs jest odniesieniem do kol 5 w tab .2-1.1 : | |
Imperfekcje projektowe ustalane zgodnie z zaleceniami normy projektowania konstrukcji stalowych [10] wyznaczano między innymi w przykładzie 3-2.1 .
⊗ ⇒ [ Geneza metod imperfekcyjnych]
Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2017-2020), Imperfekcyjna metoda projektowania konstrukcji, Encyklopedia πWiki, Wydawnictwo Chodor-Projekt, [ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]
Historia edycji:
Start (2019-04-08 do 15) wersja 1,0
(2019-05-27) Wersja 2.0: dokonano podziału rozdziału na części w celu poprawy procesu wczytywania strony
Literatura
- PN-ISO 4463-1:2012, Metody pomiarowe w budownictwie. Tyczenie i pomiar, Część 1: Planowanie i organizacja, procedury pomiarowe, kryteria akceptacji
- Tiltman K. O. (1977). Was kostet die Genauigkeitim Betonferitg-teilbau ? Baugewerbe, 5, 21–26
- Migdalski J. (Ed.). (1982), Poradnik niezawodności. Podstawy matematyczne. Wydawnictwa Przemysłu Maszynowego WEMA
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- Jacobs, J. P. (Ed.). (2010). Commentary Eurocode 2. European Concrete Platform ASBL
- Reguły ogólne i reguły dla budynków
- Wolfram, MathWorld, (2019), Mathematica. Extreme Value DIstribution, [ http://mathworld.wolfram.com/ExtremeValueDistribution.html ]
- Marsaglia G., (2006), Ratios of Normal Variables, Journal of Statistical Software, 16(4), [ http://www.jstatsoft.org/]
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
________________________________




