Niniejszy artykuł jest rozdziałem 2-2 podręcznika Imperfekcyjna metoda projektowania konstrukcji [ ← spis treści]
Nawigacja: [Imperfekcje i ich źródła] ⇐ ⊗ ⇒ [ Geneza metod imperfekcyjnych]
Artykuł w ciągu ostatnich 24 godzin czytało 1 Czytelników
[ Imperfekcje konstrukcji żelbetowych ] [poprzednie R3-3] ⇐ ⊗ ⇒ [następne R3-5] [ Imperfekcje konstrukcji drewnianych i murowych ]
Imperfekcje konstrukcji zespolonych
Przy obliczaniu stateczności konstrukcji zespolonych zgodnie z [1] należy brać pod uwagę efekty drugiego rzędu, w tym naprężenia własne, imperfekcje geometryczne, miejscową niestateczność, zarysowanie, skurcz i pełzanie betonu oraz uplastycznienie stali konstrukcyjnej i zbrojenia. Siły wewnętrzne należy określać na podstawie analizy sprężysto-plastycznej.
Zgodnie z [1],kl. 3.2. obliczanie elementów zespolonych podatnych na imperfekcje (elementów ściskanych lub smukłych belek) należy prowadzić zgodnie z ogólnymi zasadami podanymi dla konstrukcji stalowych, a wartości podstawowych imperfekcji przechyłowych przyjmować zgodnie z ( 3-2.1) do ( 3-2.4).
Imperfekcje konstrukcji aluminiowych
Zasady Eurokod 9 przykrywają zasady Eurokod 3
Postanowienia normy Eurokod 9 [2] do projektowania konstrukcji aluminiowych są w istocie poprawioną i uogólnioną wersją postanowień normy Eurokod 3 [3] . Dlatego uznajemy, że zasady podane w normie [2] mają pierwszeństwo przed [3]
Imperfekcje przechyłowe
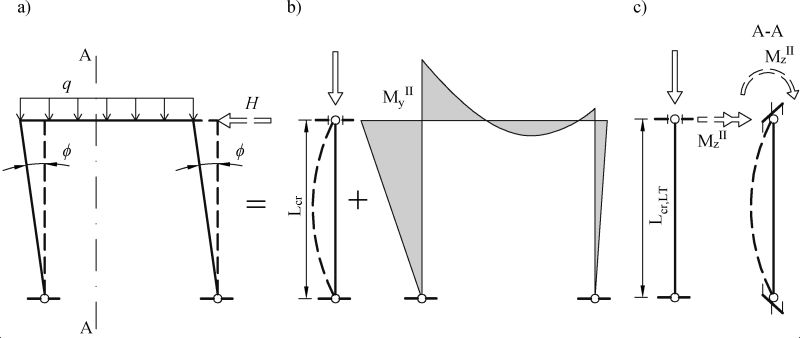
Globalne imperfekcje przechyłowe uwzględnia się przechyłem $\Phi$ (Rys. 3.4a) zgodnie z formułą ( 3-2.4) również z wartością podstawową $ \Phi_0=1/200$. Imperfekcje przechyłowe można zastąpić fikcyjnymi siłami poziomymi zgodnie z Rys. 3.2a. Wstępne imperfekcje przechyłowe uwzględnia się osobno w każdym z rozpatrywanych kierunków przechyłu W przypadku wielokondygnacyjnych szkieletów słupowo-belkowych budynków siły zastępcze przykłada się na wszystkich poziomach stropów i dachu.
Przechyły konstrukcji mogą powodować translacje lub obroty przekroju budynku (Rys. 3-4.1).
Rys. 3-4.1. Utrata stateczności ram aluminiowych: a) imperfekcje przechyłowe SGI , b) zastosowanie metody hybrydowej HIM
Ograniczenie liczby krzywych wyboczeniowych
Zgodnie z [2] lokalne imperfekcje łukowe oraz równoważne obciążenie od imperfekcji przyjmuje się zgodnie z Rys. 3.2b Wskazujemy od razu, ze zastosowanie sił fikcyjnych zgodnie z tą formułą nie zawsze jest właściwe (p. uwaga pod koniec pkt. 3.2)
Wprowadzono dwie klasy wyboczenia konstrukcji aluminiowych A i B [4],tab.3.2 , które są zależne od rodzaju stopu aluminium, ale niezależne od kształtu przekroju kształtownika W zależności od klasy wyboczenia, przyjmowane są względne strzałki imperfekcji:
- klasa A
$e_0/L= 1/300$ ($n_L=300$) w analizie sprężystej ; $e_0/L= 1/250)$ ($n_L= 250$) w analizie plastycznej, - klasa B
$e_0/L= 1/200$ ($n_L=200$) w analizie sprężystej ; $e_0/L= 1/150)$ ($n_L= 150$) w analizie plastycznej.
Przy tej okazji należy wskazać, że znaczne ograniczenie liczby krzywych wyboczeniowych również dla konstrukcji stalowych postuluje norma japońska JRA [5]. Zaleca bowiem jedną krzywą wyboczeniową położoną pomiędzy europejskim typem „b” i „c” , dla której $n_L \approx 200$ niezależnie od kształtu przekroju i typu analizy. Pokazano, że mnożenie typów krzywych wyboczeniowych nie jest statystycznie istotne, więc w praktyce nie jest potrzebne.
Postulat ograniczenia liczby krzywych wyboczeniowych konstrukcji stalowych
W niniejszej pracy stawiamy postulat, by imperfekcje łukowe konstrukcji stalowych i aluminiowych przyjmować o wartości:
$$\begin{equation} e_{0,zmod}=\cfrac {L} {200} \to n_L =200 \quad \text { dla każdego przekroju i rodzaju analizy} \label {n_Lzmod} \end{equation}$$
Hipoteza ($\ref{n_Lzmod}$) może być zweryfikowana poprzez przeprowadzenie testów statystycznych na akceptowalnym poziomie ufności, który zdaniem autora należy przyjąć o wartości 95%.
Oddziaływania poziome od imperfekcji przechyłowych na stropy i podpory budynku szkieletowego przyjmuje się zgodnie z Rys. 3.6 (analogicznie jak w konstrukcjach stalowych lub żelbetowych).
Wymóg modelowania imperfekcji łukowych
Zgodnie z [2]„] (podobnie jak [3] ) – imperfekcje łukowe generalnie mogą być pomijane (są uwzględniane przez współczynniki wyboczeniowe), ale powinny być obecne w modelu konstrukcji wrażliwych na efekty 2 rzędu, gdy co najmniej jeden węzeł końcowy elementu jest sztywny, a element jest smukły o smukłości liczonej dla pręta przegubowo-przgubowego $\overline \lambda > 0,5 \cdot\sqrt { \cfrac{A f_y}{N_{Ed}}} ( $f_y$ -granica plastyczności).
Zastosowanie metody hybrydowej
Ze względu na trudności w uwzględnieniu w modelu globalnym imperfekcji łukowych elementów oraz rozpowszechnioną metodę wyboczeniową, zaleca się, by w przypadku niepełnego uwzględnienia imperfekcji łukowych w analizie globalnej zastosować metodę HIM, zilustrowaną na Rys. 3.4b. (p. też pkt 1.3 – rozdział 1). Podobne zalecenie zawiera norma do projektowania konstrukcji stalowych [3] .
Imperfekcje skrętne
Jeśli analiza drugiego rzędu ma uwzględniać zwichrzenie elementów zginanych, to zastępcze imperfekcje tych elementów można przyjmować w płaszczyźnie najmniejszej bezwładności przekroju o strzałce równej $k e_0$, gdzie strzałka $e_0$ jest ustalona jak dla elementu ściskanego. Zaleca się $k=0,5$.
Specjalne uwzględnienie imperfekcji skrętnych na ogół nie jest konieczne, ponieważ w konsekwencji wygięcia bocznego uzyskuje się imperfekcję skrętną zgodnie z formułą (3-2.8).
⇒ [następne R3-5] [ Imperfekcje konstrukcji drewnianych i murowych ]
Niniejszy artykuł jest częścią 4 rozdziału 3 podręcznika Imperfekcyjna metoda projektowania konstrukcji
Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda projektowania konstrukcji, Encyklopedia πWiki,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]
Historia edycji:
(2019-04-19, 30) Wersja 1.0
Proszę społeczność Inżynierów w internecie o przesyłanie recenzji podręcznika na adres wydawnictwa biuro@chodor-projekt.net
Leszek ChodorLiteratura
- PN-EN 1994-1-1+Ap1+AC:2008, Eurokod 4, Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1999-1-1:2010, Eurokod 9: Projektowanie konstrukcji aluminiowych, Część 1-1: Reguły ogólne
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- (PN-EN 1999-1-1:2010, Eurokod 9: Projektowanie konstrukcji aluminiowych, Część 1-1: Reguły ogólne
- Fukumoto, Y. (1982). Numerical Data Bank for the Ultimate Strengths Steel Struc-tures. Der Stahlbau, 1
________________________________