Artykuł w ciągu ostatnich 24 godzin czytało  6 Czytelników
Uwagi i recenzje podręcznika  przesyłać na adres wydawnictwa: wydawnictwo@chodor-projekt.net lub leszek.chodor@chodor-pojekt.pl
spis treści prodręcznika: [ Imperfekcyjna metoda projektowania konstrukcji ]

Rozdział 2 :  IMPERFEKCJE I METODY PROJEKTOWANIA
Część 2-1 : Imperfekcje konstrukcji i ich źródła
iNawigacja: [ 1-2 :  Krótki przegląd metod wyboczeniowych i imperfekcyjnych ] ⇐ ⊗ ⇒  [ 2-2 : Imperfekcje projektowe z odchyłek wykonawczych ]

Źródłem geometrycznych imperfekcji systemowych są odchyłki wytwarzania elementów i wznoszenia konstrukcji. Dopuszczalne tolerancje wykonawcze są ustalone w przepisach odbiorowych, a w szczególności normach dla konstrukcji stalowych oraz  dla konstrukcji żelbetowych, a także w dokumentacji projektowej. Podstawowym składnikiem projektu wykonawczego jest specyfikacja wykonania i odbioru konstrukcji, w której mogą być utrzymane dopuszczalne tolerancje określone w normach, albo podane są indywidualne warunki wykonania i odbioru, wynikające ze specyficznych wymagań projektowych. Dopuszczalne tolerancje wykonania, warunki odbioru i  statystycznej kontroli jakości wraz z kryteriami akceptacji ostatecznie określa Projektant.
Imperfekcje materiałowe wraz z imperfekcjami geometrycznymi przekrojów elementów są ujmowane w projektowaniu poprzez współczynniki bezpieczeństwa.

Klasyfikacja imperfekcji konstrukcyjnych

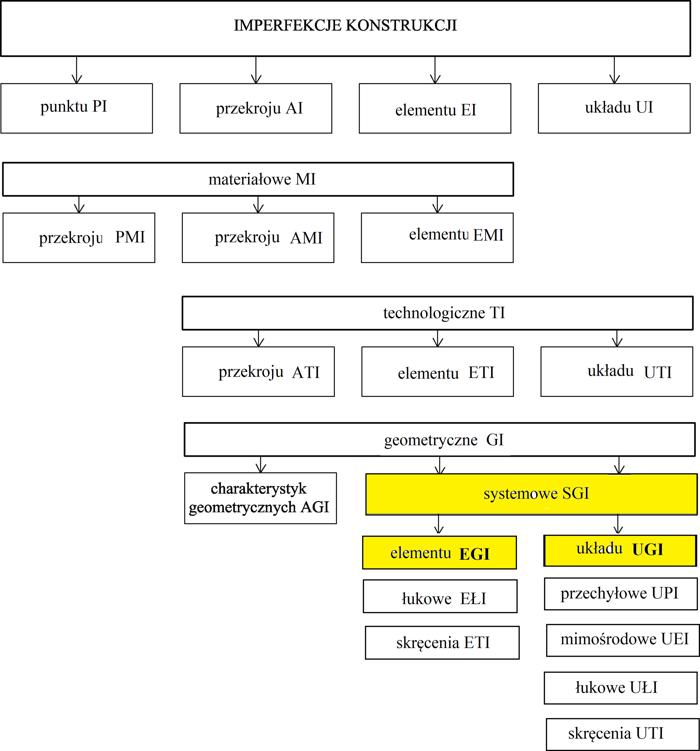
Klasyfikację imperfekcji konstrukcji zaprezentowano na Rys.1.

Rys. 1. Klasyfikacja imperfekcji konstrukcji

Imperfekcje konstrukcji można rozpatrywać na poziomie:

• PI – punktu materialnego,
• AI – przekroju, rozumianego jako zbiór punktów w przekroju ciała,
• EI – elementu, rozumianego jako oś na której ułożono przekroje,
• SI – systemu, rozumianego jako system węzłów w przestrzeni pomiędzy którymi rozpięte są elementy.

Imperfekcje mogą być :

• materiałowe

punktu PMI, wynikające ze zmienności cech materiałowych punktu:  granicy wytrzymałości, modułów odkształcalności itd.,

przekroju AMI, wynikające z losowego rozkładu charakterystyk punktów na powierzchni przekroju,

elementu EMI, wynikające z losowego rozkład cech materiału po długości osi pręta lub powierzchni środkowej płyty, tarczy, powłoki.

• technologiczne

ATI  przekroju (lub punktu), związane z naprężeniami własnymi walcowniczymi lub spawalniczymi, odkształceniami skurczowymi betonu i innymi imperfekcjami wynikającymi z jakości procesu spawalniczego lub betonowania, karbami technologicznymi itd.,

ETI  elementu, związane ze zjawiskami jak wyżej, wynikające z losowego rozkładu tych imperfekcji po długości, powierzchni lub objętości elementu,

UTI  układu elementów, związane niedokładnościami technologii montażu konstrukcji z elementów. Impefekcje te ujmiemy w geometrycznych imperfekcjach układu UGI.

• geometryczne

AGI  przekroju, objawiające się odchyleniami rzeczywistych wymiarów od wymiarów nominalnych i w konsekwencji odchyleniami charakterystyk geometrycznych: pola przekroju, momentów statycznych oraz bezwładności,

SGI  systemowe, które mają swoje źródło w wytwórczych i montażowych odchyłkach położenia osi elementów i węzłów konstrukcji od idealnego (projektowanego) kształtu.

Wśród imperfekcji systemowych SGI wyróżnimy:

EGI  imperfekcje elementu, wynikające z odchyleń geometrii elementu na długości, powierzchni lub objętości pomiędzy węzłami brzegowymi. Imperfekcje elementu nazywane są często imperfekcjami lokalnymi

UGI imperfekcje układu elementów, wynikające z odchyleń węzłów brzegowych elementów składowych od położenia projektowanego. Imperfekcje układu nazywane są często imperfekcjami globalnymi,

Imperfekcje globalne UGI są to niewielkie mimośrody montażowe, występujące w węzłach konstrukcji nieobciążonej:  przesunięcia osi płaszczyzn belek słupów i innych elementów w poziomie, pionie oraz skręcenia, objawiające się niedoskonałościami położenia elementów w stosunku do siebie: brak prostopadłości, prostoliniowości płaskości przylegania, itd.

Wśród imperfekcji układu UGI (globalnych) można wyróżnić:

UPI – przechyłowe, objawiające się przechyłem układu elementów w stosunku do pionu
UEI – mimośrodowe, pochodzące od mimośrodowego wykonania węzłów brzegowych (np. głowic i stóp słupów)
UŁI – łukowe, objawiające się wygięciem układu elementów w przestrzeni (węzły brzegowe układają się na łuku, a nie na prostej)
UTI – skręcenia, objawiające się skręceniem układu elementów w przestrzeni

Wśród imperfekcji globalnych UGI ustala się imperfekcję zastępczą, która integruje w sobie wszystkie  imperfekcje geometryczne układu. Najczęściej imperfekcją zastępczą jest imperfekcja przechyłowa UPI.

Imperfekcje lokalne EGI są to wstępne wygięcia i skręcenia, a także spaczenia elementów pomiędzy węzłami końcowymi elementu. 

Wśród imperfekcji elementu EGI można wyróżnić:

EŁI – łukowe, objawiające się wygięciem osi elementu w przestrzeni (węzły wewnętrzne układają się na łuku, a nie na prostej)
ETI – skręcenia, objawiające się skręceniem elementu w przestrzeni.

Wśród imperfekcji lokalnych EGI ustala się imperfekcję zastępczą, która integruje w sobie wszystkie  imperfekcje geometryczne elemntu. Najczęściej imperfekcją zastępczą jest imperfekcja łukowa EŁI.

W pracy nie zajmujemy się imperfekcjami materiałowymi (PMI, AMI, ATI), technologicznymi (ATI, EMI, ETI), a także imperfekcjami geometrycznymi przekroju AGI. W sposób wystarczający dla praktyki imperfekcje te są uwzględniane przez system częściowych, materiałowych współczynników bezpieczeństwa, który omówiono  na wstępie do rozdziału 3.

Zajmiemy się natomiast geometrycznymi  imperfekcje systemowymi SGI (UGI oraz EGI).

W dalszej części pracy imperfekcje Globalne ( układu, przechyłowe) będziemy  oznaczali indeksem „_G„, a imperfekcje Lokalne  (elementu, łukowe) będziemy oznaczali indeksem „_L„.

Modele imperfekcji

Model imperfekcji globalnych

Imperfekcje globalne UGI są  zastępowane jedną zastępczą imperfekcją przechyłową UPI.

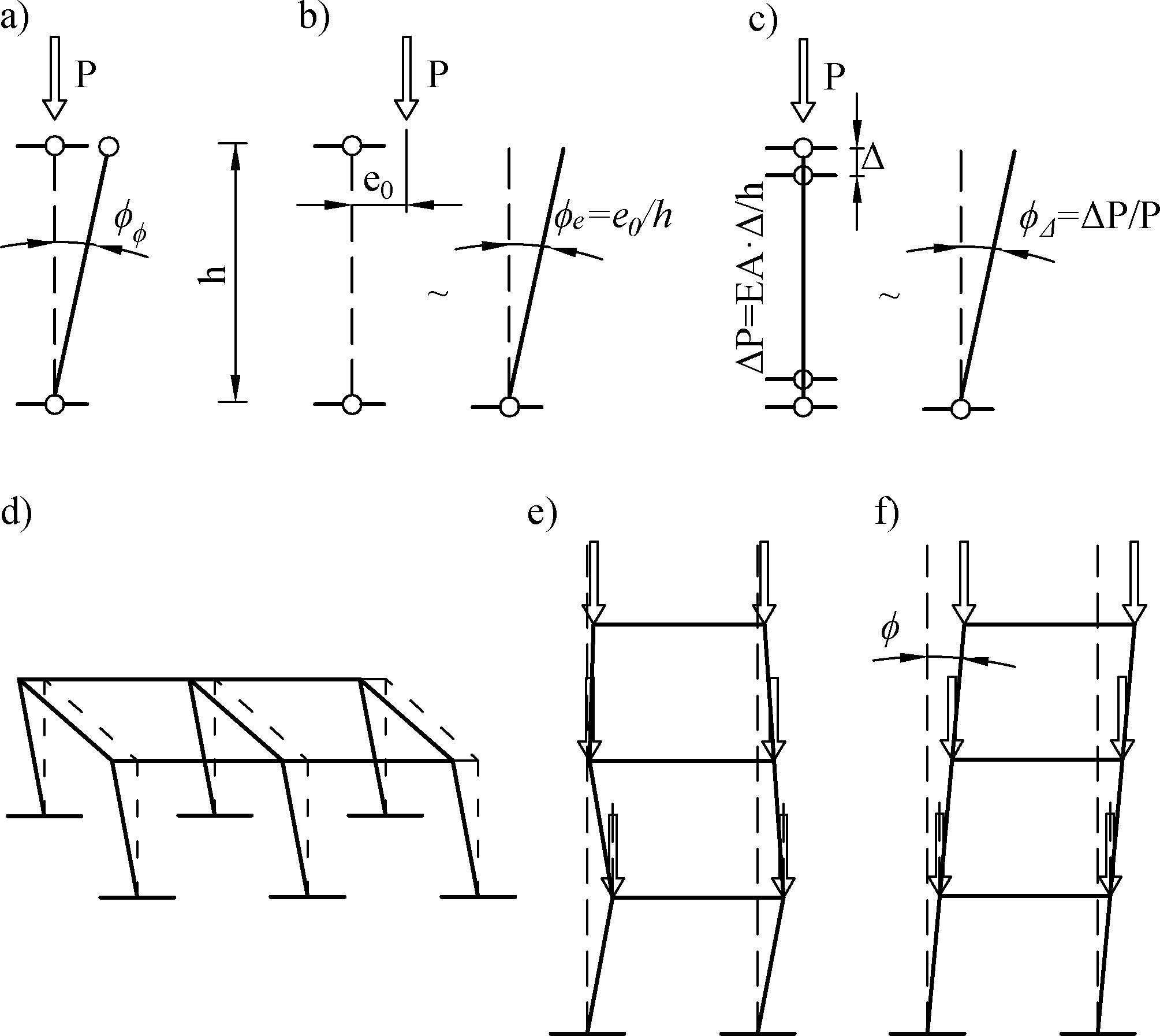
Rys. 2. Imperfekcje przechyłowe: a) źródło imperfekcji, b) imperfekcje oddzielnych słupów, c) zastępcza imperfekcja przechyłowa (opracowano na podstawie [1]

Imperfekcje przechyłowe słupów mają różne źródła, które wystąpią podczas prefabrykacji oraz wznoszenia i objawiają się przychyleniem konstrukcji rzeczywistej w stosunku do idealnej konfiguracji. Źródła imperfekcji przechyłowych zostały zilustrowane na Rys. 2

Koncepcja obliczeniowa tych imperfekcji przewiduje, że są to zastępcze imperfekcje geometryczne położenia węzłów układu konstrukcyjnego w przestrzeni, obejmujące: odchylenie elementu od pionu (Rys_2.a), mimośrody wykonawcze w głowicy i stopie słupa (rys.2b), zamontowanie elementu krótszego od idealnego (rys.4.6c), ale także wielu słupów na wybranej kondygnacji (rys.2d), i w końcu słupów na wielu kondygnacjach (rys.2e). Wszystkie te imperfekcje są zastępowane jedną imperfekcją , czyli kątem odchylenia konstrukcji od pionu, pokazanym na rys2.f). Czasami do tych imperfekcji włącza się również błędy montażu w stykach elementów pomiędzy węzłami końcowymi, choć przeważa pogląd, że tego typu imperfekcje są imperfekcjami lokalnymi, a mogę być włączone do imperfekcji globalnych wyłącznie w przypadku, gdy węzeł elementu będzie przyjęty w miejscu styku wewnętrznego i wówczas staje się stopą lub głowicą elementu.

Imperfekcje przechyłowe GGI były przedmiotem szerokich badań (np. [2], [3], [1], [4], [5] i in.). W pracach tych pokazano, że statystycznie nieistotna jest korelacja pomiędzy przechyłami, a także korelacja z innymi początkowymi imperfekcjami słupów na tych samych kondygnacjach.

Model  imperfekcji lokalnych

Najczęściej kształt loklanych imperfekcji łukowych  przyjmuje się w postaci sinusoidy (np. [6], [7]), [8], , [9], [10],[11], [12], [13], [14], [15] ) lub paraboloidt. Nie jest to jednak w sposób wiarygodny potwierdzone statystycznymi metodami na podstawie pomiarów elementów i konstrukcji rzeczywistych [16] .

W pracy [17] zastosowano uogólnienie i łukowe imperfekcje słupów aproksymowano szeregiem Fouriera, tak aby funkcja wstępnego ugięcia spełniała kinematyczne warunki brzegowe, co regulowano częstotliwością, a wartość amplitudy (strzałka wstępnego wygięcia)  była dobierana na podstawie regresji  z danymi eksperymentalnymi doświadczeniem i dopuszczalnych tolerancji, określonych w przepisach do odbioru konstrukcji.

Zastępcza imperfekcja łukowa

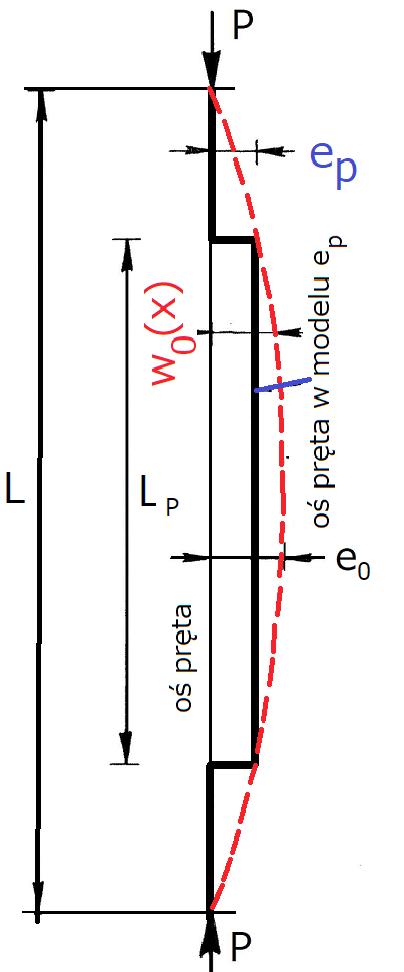
Imperfekcje lokalne  EGI są  zastępowane jedną zastępczą imperfekcją łukową EŁI ze strzałką wygięcia $e_0$ na bazie $L$  pomiędzy węzłami końcowymi elementu (rys.3).

Model imperfekcji lokalnych EŁI, jest wstępnym wygięciem pręta $w_0(x)$ pokazanym na rys. 2-1.3, przyjmowanym w kształcie sinusoidy

$$ \begin{equation} w_0(x)=e_0 \sin{\pi x/L} \label {1}\end{equation}$$

Imperfekcja $w_0(x)$ jest wstępnym wygieciem w płaszczyźnie pręta i integruje w sobie wszystkie geometryczne imperfekcje pręta w tej płaszczyźnie i dlatego jest nazywana imperfekcją zastępczą.

Analogicznie definiuje się imperefkcję – wstępne wygięcie z płaszczyzny pręta

$$ \begin{equation} v_0(x)=e_{v,0} \sin{\pi x/L} \label {2}\end{equation}$$

Rys. 3. Model imperfekcji łukowych (opis w tekscie)

Zastępcze wstępne skręcenia

W przypadku belek, istotne są lokalne imperfekcje w postaci wstępnych skręceń $\varphi_{x,0}$ wokół osi własnej pręta (x).

Pomiędzy kątem skręcenia $\varphi_x (x) $  oraz bocznym wygięciem $v(x)$ nie ma formalnego związku różniczkowego, ale istnieje związek pomiędzy obciążeniem pionowym $F_z$ które na wygięciu$v(x)$ wywołuje moment skręcający $M_x=F_z\cdot v(x)$.

Kąt wstępnego skręcenia  $\varphi_{x,0}$ szacujemy przy założeniu, że wstępne boczne wygięcia łukowe $v_0$, dotyczy pasa górnego (1) i dolnego (2) belki o wysokości H, ale są wygięte w przeciwne strony o wartość stanowiącą 50% imperfekcji łukowego wygięcia z płaszczyzny zginania $v_0$, to znaczy

$e_{v,0(1)}=- e_{v,0(2)}= e_{v,0} / 2$.

Tutaj $e_{v,0}$ jest strzałką bocznego wygięcia wstępnego. Mamy stąd oszacowanie amplitudy wstępnego skręcenia:

$$\begin{equation} \varphi_0 =\cfrac{e_{v,0}/ 2}{H/2}=\cfrac{e_{v,0}} {H}  \label {3} \end{equation}$$

gdzie: H – wysokość belki.

Zastępczy mimośród  przyłożenia siły – nie istnieje

Często, szczególnie w konstrukcjach żelbetowych geometryczną imperfekcję łukową zastępuje się mimośrodem niezamierzonym $e_P$ (rys. 1).

Zamiana taka nie jest jednoznaczna, bo wstępują w niej trzy wielości $e_0$, $e_P$ oraz $L_P$. Zależność między tymi zmiennymi wyznaczymy metodą energetyczną. Sprawdzimy przy tym dokładność i w ogólności dopuszczalność zastąpienia imperfekcji łukowej przez mimośród przyłożenia siły.

Potencjalna energia sprężysta pręta wstępnie wygiętego w łuk ($\ref {1}$) przed obciążeniem wynosi:

$$ \begin{equation} \Pi_0 = \int \limits_0^L  \cfrac{EI}{2} \cdot [ w_0 ^”(x)]^2  dx =  \cfrac{\pi^4 EI}{4 L^3} \cdot e_o^2 \label {4} \end{equation}$$

Na skutek ściskania siłą $P$  pręt zostanie dogięty do stanu

$$ \begin{equation} w(x)= a_\Lambda \cdot w_0(x) \label {5} \end{equation}$$

gdzie współczynnik amplifikacji (1-2-1.12) wynosi   $a_\Lambda=\cfrac{1}{1-1/\Lambda_{cr}}=\cfrac{1}{1-P/P_{cr}}$, Wobec tego energia potencjalna zwiększy się do:

$$ \begin{equation} \Pi_w = \int \limits_0^L  \left ( \cfrac{EI}{2} \cdot [ w ^{„} (x)]^2  -\cfrac {P}{2}  \cdot [ w ^{’}(x)]^2 \right ) dx =a_\Lambda^2 \cdot\left[ \Pi_0 -\left( \cfrac{\pi e_0}{2L} \right)^2 \cdot PL \right]    \label {6} \end{equation}$$

Drugi czynnik w wyrażeniu  ($\ref{6}$)  zeruje  się po osiągnięciu przez obciążenie wartości $P=P_{cr}= \cfrac{\pi^2 EI}{L^2}$, ale jednocześnie $a_\Lambda = \infty$ Granicę do której dąży $\Pi_w$  symbolicznie zapiszemy w postaci $\infty^2 \cdot 0 =\infty$.  Po przekształceniach ($\ref{6}$) można zapisać w postaci

$$ \begin{equation} \Pi_w = \cfrac{n_e}{4} \cdot \cfrac{P_{cr}^2}{P-P_{cr} }\label {7} \end{equation}$$

gdzie $n_e=n_L=e_0/L$ względna miara imperfekcji łukowej $n_e$ i lokalnej $n_L$ .

W wyrażeniu ($\ref{7}$) jawnie pokazano, że energia potencjalna ściskanego pręta z imperfekcją łukową jest proporcjonalna do tej imperfekcji oraz kwadratu siły krytycznej pręta  oraz szybko zwiększa się przy zbliżaniu się $P$ do obciążenia krytycznego.

Energia potencjalna, która byłaby wprowadzona do prostego pręta na długości $L_p$ na skutek zginania momentem $M=P\cdot e_P$  wynosi:

$$ \begin{equation} \Pi_e = \int \limits_0^{9} \left( \cfrac{(P\cdot e_P)^2} {2 EI} +\cfrac{P^2}{2EA} \right ) dx = \cfrac{P^2 L_p}{2 EI} (e_P^2  + EI/EA) \label {8] \end{equation}$$

Po rozwiązaniu równania ($\ref{7}$)=($\ref{8]$) względem $L_p$ otrzymujemy:

$$ \begin{equation} L_p= \cfrac {n_e}{2 EI }  \cdot (e_P^2+EI/EA) \cdot \cfrac{ (P_{cr}/P)^2}{P-P_{cr}}  \label {9} \end{equation}$$

Dla często spotykanego przypadku zamiany imperfekcji łukowej siłą przyłożona do głowicy pręta na mimośrodzie $e_P$ , czyli dla $L_p=L$ z rozwiązania ($\ref{7}$)=($\ref{8]$) względem $e_P$ uzyskujemy:

$$ \begin{equation} e_p= \sqrt { \cfrac{n_e EI}{2L} \cdot \cfrac{(P_{cr}/P)^2}{P-P_{cr}}-\cfrac{EI}{EA}} \label {10} \end{equation}$$

Z wyrażenia ($\ref{10}$) wynika wprost, że dla żadnej siły w stanie przedkrytycznym i krytycznym $P \le P_{cr}$ nie istnieje mimośród zastępczy $e_P$, który można wprowadzić  w miejsce imperfekcji łukowej. (ujemne wyrażenie pod pierwiastkiem). Natomiast wystąpienie siły $P>P_{cr}$ jest fizycznie niemoźliwe.
W szczególności nie jest właściwe przyjęcie mimośrodu $e_P=e_0$.

Podobne wnioski uzyskamy po zastosowaniu metody przemieszczeniowej, tzn po próbie doboru takiego mimośrodu $e_P$, by działanie siły $P$ na tym mimośrodzie wywołało w środku pręta ugięcie $e_0$. Natomiast  zastosowanie kryterium statycznego prowadzi do $e_P=e_0$, co daje błędne wyniki, jak pokazano w dalszej części podręcznika.

Miara imperfekcji

Tolerancje wykonawcze oraz  imperfekcje projektowe wyrażamy bezwymiarowo:

$$\begin {equation} n_\Delta= \cfrac{B}{\Delta} \label {11} \end {equation}$$

gdzie $n_\Delta$  jest ogólnie wartością tolerancji wykonawczej lub amplitudą imperfekcji wstępnego wygięcia lub mimośrodu [mm] lub wychylenia , a $B$ [mm] jest bazą, do której odnosi się tolerancję lub imperfekcję. Baza jest najczęściej długością pręta $L$ lub wysokością budowli $H$. W celu wyróżnienia rodzaju imperfekcji często stosuje się odpowiedni indeks wskaźnika ($\ref {11}$), na przykład:

$n_G$ -imperfekcje globalne  (najczęściej przechyłowe),
$n_L$ – imperfekcje lokalne  (najczęśniej łukowe).

Losowa natura imperfekcji systemowych

Mimo intensywnych badań nad problemem imperfekcji prowadzonych od lat 50-tych poprzedniego wieku (m.in. [18], [19], [20], [9],[21], [22], określenie zależności pomiędzy podejściem normowym, teorią konstrukcji, pomiarem imperfekcji, a wartościami obciążenia prowadzącego do utraty stateczności lub wytrzymałości jest nadal niekompletne.W licznych badaniach systematycznie obserwuje, że:

• zestaw imperfekcji konstrukcji jest trudny do przewidzenia,
• Możliwe imperfekcje geometryczne cechuje znaczne zróżnicowanie pod względem ich kształtu, zasięgu (wielkości), ilości, rozkładu oraz amplitudy.
• trudno jednoznacznie ustalić poziom niebezpieczny tychże imperfekcji, jako że dla różnych typów obciążenia konstrukcji, różne imperfekcje mogą być mniej lub bardziej niebezpieczne dla funkcjonowania ogółu budowli.

Zgodnie stwierdza się więc, że analiza imperfekcji konstrukcji  oraz ich wpływu na nośność konstrukcji nie powinna być prowadzona w sposób deterministyczny, a powinna uwzględniać  losowy charakter wstępnych niedoskonałości. Zastosowanie zaawansowanego aparatu teorii niezawodności byłoby jednak  zbyt kosztowne i złożone, przy wielkiej liczbie stopni swobody (wymiarze losowych pól imperfekcji).

W takiej sytuacji zaleca się analizować model konstrukcyjny z maksymalnie ograniczoną liczbą zmiennych losowych istotnych poprzez włączenie w te zmienne istotne, rozproszenia innych, mniej ważnych zmiennych, a także przyjmowanie najprostszych, liniowych modeli losowych.
Istotną zmienną losową wpływającą na nośność konstrukcji są systemowe imperfekcje geometryczne (UGI i EGI) takiego doboru dokonano w normach Eurokod. Zastępczą imperfekcją globalną jest imperfekcja przechyłowa a, zastępczą lokalną imperfekcja łukowa.

Systemowe imperfekcje geometryczne są traktowane szczególnie, bowiem swoim zaistnieniem w konstrukcji mogą wywołać efekty niemożliwe do opisania i przewidzenia nawet przy dokładnie wykalibrowanych współczynnikach bezpieczeństwa materiału i obciążenia. Systemowa imperfekcja geometryczna jest zastępczą zmienną losową, która integruje wszystkie odchylenia geometryczne i część materiałowych (np. naprężenia własne) oraz niedokładności modelu konstrukcji. Normy Eurokod 2, 3, 4, 5, 6 i 9 uporządkowały bazę danych o imperfekcjach i wskazały na konkretne aproksymacje, które można stosować w praktycznym projektowaniu.

Imperfekcje systemowe (geometryczne globalne- przechyłowe  i lokalne – łukowe )  należy traktować jako pole losowe lub w jako proces stochastyczny w szerokim sensie, czyli jako rodzinę zmiennych losowych indeksowaną za pomocą pewnego nielosowego parametru t (p. Dodatek A) . 

Dla teorii i praktyki inżynierskiej istotne jest oszacowanie ekstremalnych (maksymalnych lub minimalnych) imperfekcji systemowych, co dokonuje się poprzez badanie  losowego wektora $[X] =[X_1,…X_n] $  przedstawionego w postaci uporządkowanego ciągu od wartości najmniejszej do największej. Teoria losowych wartości ekstremalnych jest syntetycznie przedstawiona w Dodatku B. W podręczniku stosujemy typ I rozkładu wartości maksymalnych, czyli rozkład Gumbela.

Dopuszczalne tolerancje wykonania

Dopuszczalne odchyłki wykonania  (tolerancje wykonania)  systemów i elementów konstrukcyjnych zestawiono w tab.1 do tab.4 dla najczęściej stosowanych materiałów konstrukcji. W tych tabelach symbolem $n_p$ oznaczono imperfekcje stosowane w projektowaniu , a tolerancje wykonawcze symbole $n_w$. Wartość wskaźnika imperfekcji ($\ref{11}$) oscyluje wokół liczby 200. W normach i innych przepisach często przedstawia się odwrotność tego wskaźnika, wskazując, że imperfekcja przechyłowa wynosi np. $\Phi=1/200$. Konwencja operowania podzielnikiem jest często stosowana w programach komputerowych i upraszcza zapis.

Konstrukcje stalowe

Tolerancje wykonawcze konstrukcji stalowych podano w normie [23], a imperfekcje projektowe w normie [24], Zestawienia w tabeli wykonano dla 1 klasy tolerancji wykonania. Klasę tolerancji 1 przyjmuje się przez domniemanie i określa się ją, jako normalną. Funkcjonuje również klasa 2 tolerancji, która dotyczy elementów wrażliwych na odchyłki, np. fragmentów konstrukcji, z którą łączy się elewację szklaną. Dla klasy 2 dopuszczalne tolerancje są szacunkowo dwukrotnie mniejsze (ostrzejsze wymogi).

Obliczeniowe mimośrody wstępne $n_p$, przyjmowane do obliczania sił imperfekcji są większe od tolerancji wykonania dla elementów i budowli $n_w$, co oznacza, że w normowych zaleceniach uwzględniono, naprężenia resztkowe (walcownicze i spawalnicze), a także to, że element może być faktycznie wbudowany w konstrukcję z odchyłkami większymi od tolerancji granicznych a także to, że w trakcie eksploatacji obiektu mogą nastąpić zmiany imperfekcji na skutek zużywania się obiektu.
W tabeli zastosowano współczynnik bezpieczeństwa dla imperfekcji konstrukcji $\gamma_{i} =2$. Ideę współczynnika imperfekcji przedstawiono w kolejnym rozdziale.

Tab. 1.  Porównanie imperfekcji projektowych [24]
z wybranymi dopuszczalnymi tolerancjami konstrukcji stalowych [23]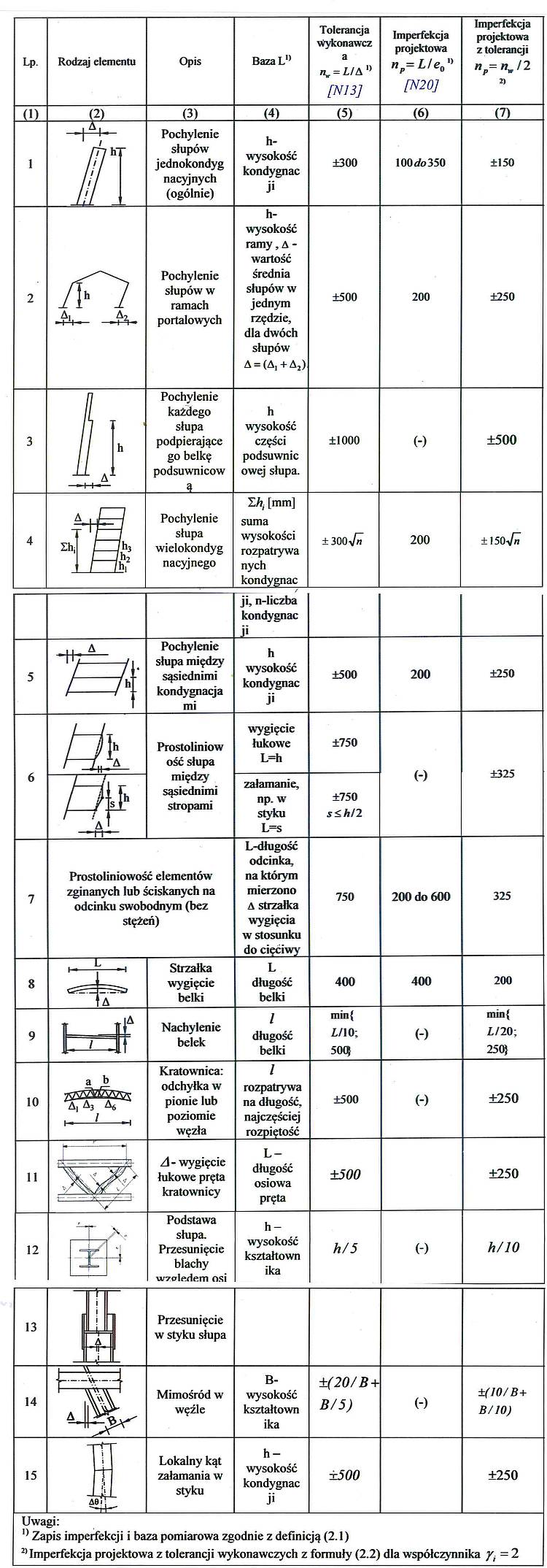

Konstrukcje żelbetowe

Dopuszczalne odchyłki wykonania elementów i konstrukcji żelbetowych zawiera norma [25]. Zalecane w projektowaniu konstrukcji żelbetowych niezamierzone mimośrody podano w normie [26].

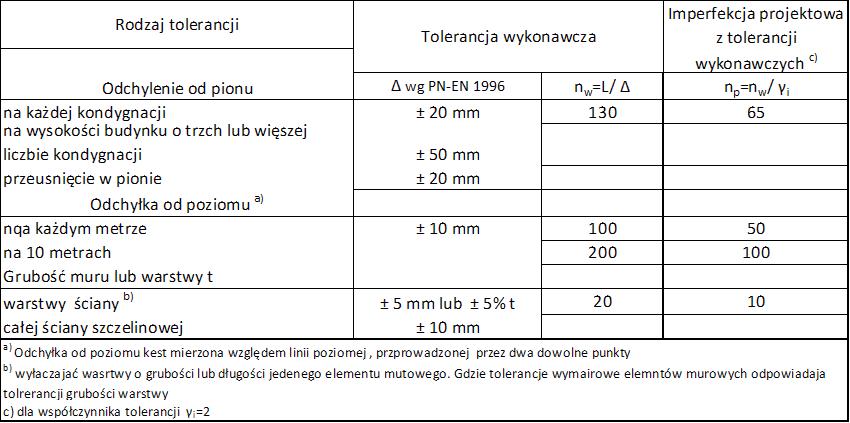
W tab.2 porównano najważniejsze projektowe imperfekcje przechyłowe i mimośrody konstrukcji żelbetowych, z dopuszczalnymi tolerancjami $\Delta$ .

Tab. 2. Porównanie dopuszczalnych tolerancji wykonawczych
elementów żelbetowych $n_w$ [25] z imperfekcjami projektowymi $n_p$ [26]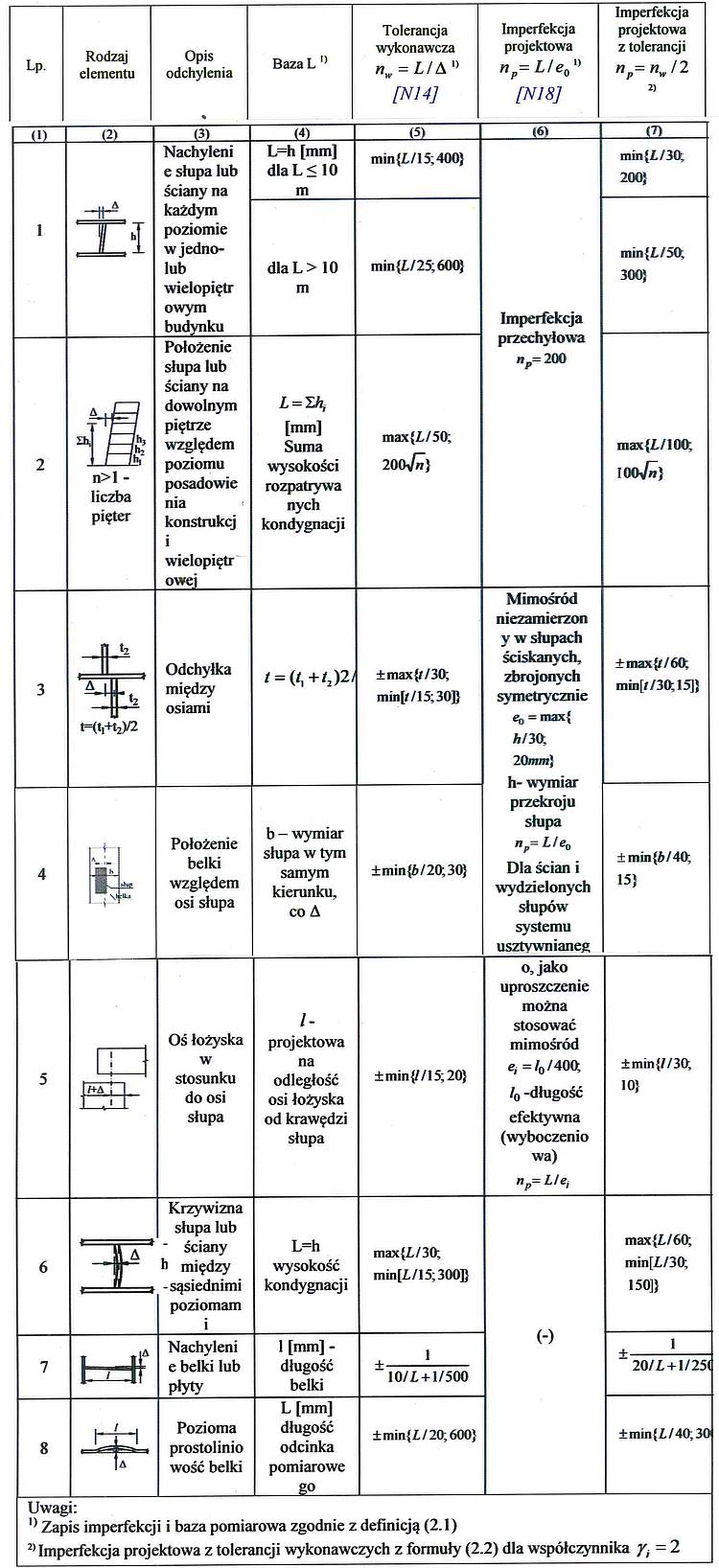

Konstrukcje drewniane

W klauzuli  [27], kl. 9.2.5.2. wymaga się, by początkowe odchyłki od prostoliniowości pojedynczych elemntów ściskanych, wymagających bocznego podparcia o rozstawie a  nie przekraczały  a!500 – dla elementów klejonych warstwowo lub wykonanych z LVL, i a/300 – dla innych elementów.

Natomiast w [27], kl.10.2(1) wymaga się, by  odchyłki od prostoliniowości słupów, belek i elementów ram, mierzone w połowie odległości pomiędzy podporami, w przypadku, gdy są narażone na utratę stateczności, jeśli są wykonane z drewna warstwowo klejonego lub LVL, nie powinny być większe niż 1/500 długości, a jeśli są  wykonane z drewna litego, nie powinny być większe niż 1/ 300 długości.

Oznacza to, że imperfekcje projektowe w przypadku konstrukcji drewnianych dotyczą prętów pomiędzy podporami , a także to ,że wyliczone  z odchyłek wykonawczych byłyby większe niż jawnie zadane w kl. [27],(5.2) .

Konstrukcje murowe

Dopuszczalne odchyłki wykonawcze konstrukcji murowych określono w [28], tab.3.1..

Tab.3 Odchyłki wykonawcze konstrukcji murowych (opracowano na podstawie [28], tab.3.1.

Belki podsuwnicowe

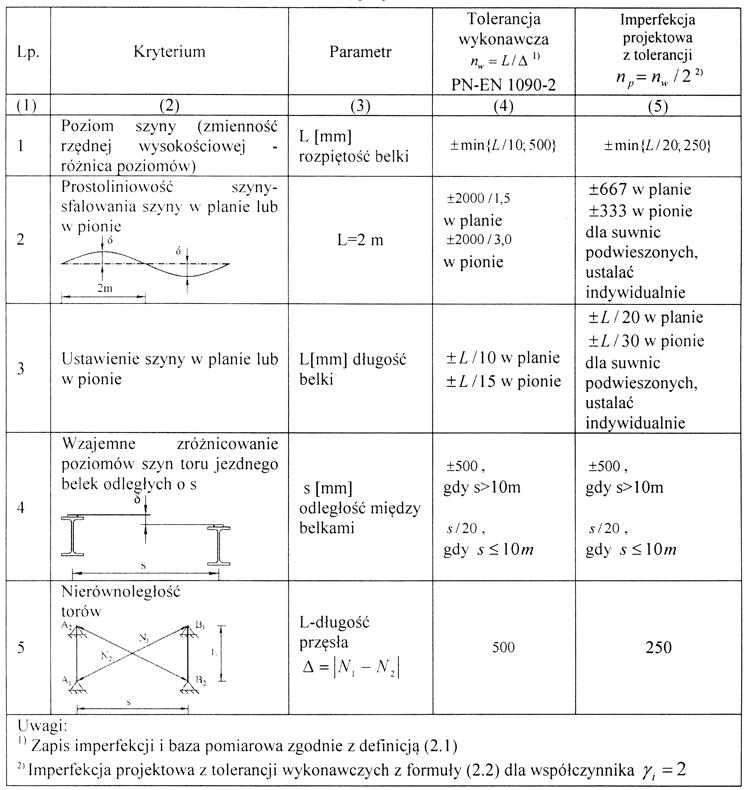
Ważną klasą konstrukcji z imperfekcjami są belki podsuwnicowe, wyposażone w tory jezdne dźwignic. Wybrane tolerancje montażu belek podsuwnicowych zestawiono w tab.4, sporządzonej na podstawie [23], tab. D.2-1.21. W przypadku suwnic mostowych podpartych, odchyłki położenia szyny powinny być regulowane podczas użytkowania konstrukcji wsporczej, a odchyłki z wiersza 1 i 4 będą dotyczyły belki konstrukcji. W przypadku suwnic mostowych podwieszonych belka jest jednocześnie torem jezdnym i dotyczą ją dodatkowo imperfekcje określone w wierszu 5.T

Tab. 4. Dopuszczalne tolerancje montażu belek podsuwnicowych i szacunkowe imperfekcje projektowe

⇒ [Imperfekcje projektowe z odchyłek wykonawczych]

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2017-2020), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki, Wydawnictwo Chodor-Projekt,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Historia edycji:
(2019-04-08 do 15) Wersja 1.0
(2019-05-05) Wersja 1.2: dodano rozdziały „Odchyłki konstrukcji drewnianych” oraz „Odchyłki konstrukcji murowych”
(2019-05-27) Wersja 2.0: dokonano podziału rozdziału na części w celu poprawy procesu wczytywania strony 

 Literatura

1. Gwóźdź M., Machowski A. (2011). Wybrane badania i obliczenia konstrukcji budowlanych metodami probabilistycznymi. Wydawnictwo Politechniki Krakowskiej
2. Beaulieu D., Adams P. F. (1978), The Results of a Survey on Structural Out-of-plumbs. Canadian Journal of Civil Engineering, 5, 642–470
3. Lindner J., Gietzelt R. (1984), Evaluation of Imperfections of Support-Elements. Stahlbau, 4, 97–98
4. Machowski A. (2002), Initial Random Out-of-plumbs of Steel Frame Col-umns. Archives of Civil Engineering, XLVIII(2), 2017–2226
5. Machowski A., Tylek I. (2012), Random Equivalent initial bow and Tilt in Steeel Frame. Advanced Steel Construction, 8(4), 383–397
6. Alveranga A. R., Silveira E. A. (2009), Second-order plastic-zone analysis of steel frames- Part II effects of initial geometric imperfection and residual stress. Latin American Journal of Solids and Structures, 6(4), 323–342
7. Beck A. T., Doria A. S. (2008), Reliability Analysis of I-Section Steel Columns de-signed according to new Brazilian Building Codes. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 3(2
8. Buonopane S. G., (2008), Strenght and Reliability of Steel Frames with Random Properties, Journal of Structural Engineering, ASCE, 134, (2), pp. 337-344
9. Hajjar J. F. (1997), Effective lenght and Effective length and notional load approach-es for assesing frame stability : Implication for American Steel. Technical Report. Task Committee on Effective Length of the Technical Committee on Load and Re-sistance Factor Design of the Technical Division of the Structural Engineering Insti-tute of the American Society CIvil Engineers
10. Gwóźdź M. (1997), Zagadnienia nośności losowej prętów metalowych. Praca dok-torska, no. Zeszyt Naukowy 69, Politechnika Krakowska
11. Kala Z. (2003), The influence of initial curvature of the axis upon the member ulti-mate strength. Journal of Structural Mechanics, 36(1), 3–14.
12. Kim S. E., Lee D. H. (2002), Second-order distributed plasticity analysis of space steel frames. Journal of Engineering Mechanics, 24, 735–744
13. Kounadis A. N., Economou A. F. (1984), The effects of Initial Curvature and other parameters the nonlinera buckling of simple frames. Journal of Structural Mechan-ics, 12(1), 27–42
14. Smith-Pardo J. P., Aristizabal – Ochoa J. D. (1999), Buckling Reversalas of Axially Restarined Imperfect Beam-Column. Journal of Engineering Mechanics, 125(4), 401–409
15. Xu L., Wang X. H. (2008), Storey-base column effective lenght faactos with accounting for initial geometric imperfections. Engineering Structures, 30(12), 3434–3444
16. Singer J., Arbocz J., Weller T. (1998), Buckling Experiments: Experimental Meth-ods in Buckling of Thin-Walled Structures Vol1: Basic Concepts, Columns, Beams and Plates Vol 2: Shells, Built-Up Structures,Composites , Additional Topics. John Wiley & Sons
17. Ersvik O. (1978), Nonlinear analysis of beam-column structures and influence of imperfections
18. Babcock C. D. (1974), Experiments in shell buckling, In: Thin Shell Structures, Theo-ry, Experiment, and Design. Prentice-Hall, Englewood Cliffs
19. Degenhard R., i in. (2007), Experiments on buckling and postbuckling of thin-walled v CFRP structures using advanced measurements systems. Int. J. Struct., Stability and Dynamics, 07(02), 337–358
20. Elishakoff I., Arbocz J. (1985), Reliability of axially compressed cylindrical shells with general nonsymmetric imperfections. Journal of Applied Mechanics, 1985(52), 122–128
21. Koiter W.T., (1945) The stabillity of elastic equilibrium, PhD Thesis, Royal Nether-lands Academy of Arts and Sciences, Amsterdam
22. Thom, R. (1972). Stabilite Structurelle et Morphogenese, Benjamin, New York
23. PN-EN 1090-2+A1:2012, Wykonanie konstrukcji stalowych i aluminiowych – Część 2: Wymagania techniczne dotyczące konstrukcji stalowych
24. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
25. PN-EN 13670:2011: Wykonywanie konstrukcji z betonu
26. PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
27. PN-EN 1995-1-1+A2+NA+07E :2010, Eurokod 5: Projektowanie konstrukcji drewnianych, Część 1-1: Postanowienia ogólne – Reguły ogólne i reguły dotyczące budynków
28. PN-EN 1996-2:2010, Eurokod 6. Projektowanie konstrukcji murowych – Część 2: Wymagania projektowe, dobór materiałów i wykonanie murów

________________________________