Leszek Chodor, 7 września 2016
07-03-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 9 Czytelników
Blachownica jest dźwigarem o przekroju poprzecznym zespawanym z blach. W przypadku belek najczęściej stosuje się blachownice z przekrojem dwuteowym (rys. 6), żebrowane (rys. 7, 8 ) i o zmiennej sztywności po długości (rys.9, rys.12 ). Sprawdzanie nośności blachownic jest dość żmudne w podejściu ręcznym, dlatego należy założyć, że obliczenia sprawdzające projekt blachownic dokonywane są z użyciem programów lub arkuszy obliczeniowych. W artykule przedstawiono najważniejsze zagadnienia związane z projektowaniem i weryfikacją blachownic, które powinny być zaimplementowane w oprogramowaniu inżynierskim.
Wprowadzenie
Przegląd problemów związanych z halami pełnościennymi (blachownicowymi) zawarto w artykule [1]. Przegląd problemów, dotyczących ram z ryglem pełnościennym zawarto również w pracy [2].
Systemy hal pełnościennych
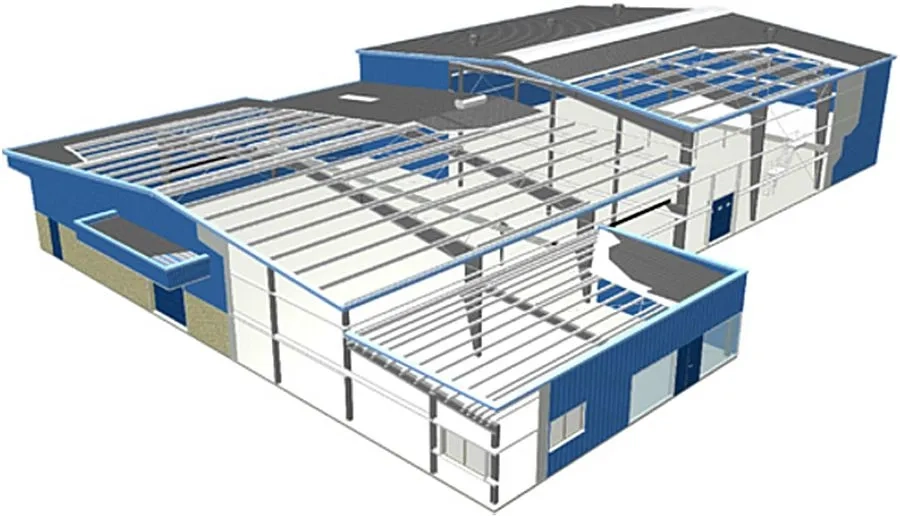
Pełnościenne rygle ram tradycyjnie stosowano w halach dostosowanych do pracy suwnic. natorowych lub podwieszonych, Ze względu na zmechanizowany sposób produkcji dwuteowników spawanych w tym o zbieżnej wysokości i ze środnikami profilowanymi ramy pełnościenne obecnie są coraz częściej stosowane w powszechnym budownictwie hal stalowych, produkowanych w systemach typu Astron (rys.1) , Butler (rys.2), ZemanHDF i innych.
Rys.1 System hal ASTRON [3]
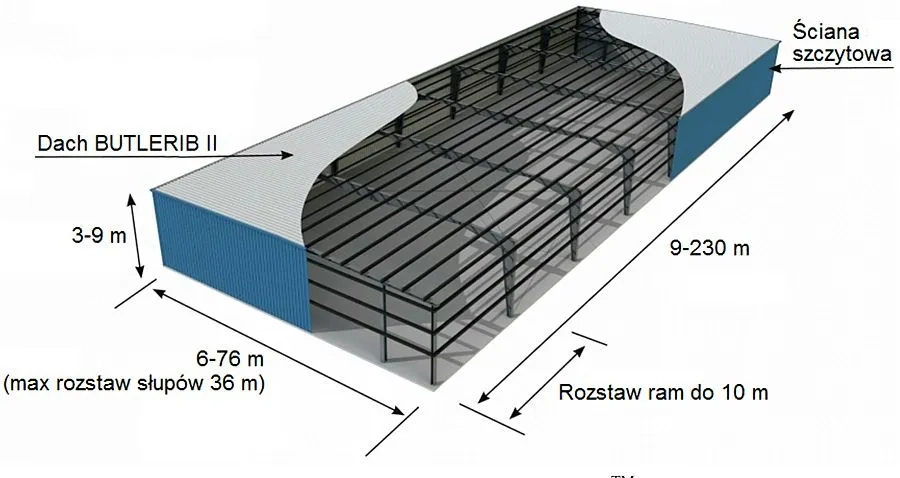
Rys. 2 System hal BUTLER Classic IITM [4]
W stosunku do konstrukcji kratowych dżwighary pełnościenne odznaczają się mniejszą pracochłonnością wytwarzania, łatwiejszym zabezpieczeniem przed korozją i ogniem oraz mniejszą wysokością konstrukcyjną, a zużycie stali w racjonalnie zaprojektowanej konstrukcji pełnościennej jest porównywalne, a może być nawet (przy zastosowaniu specjalnych rozwiązań) mniejsze niż w konstrukcji kratowej [5], [6]. Na rys. 3 pokazano ekonomiczną konstrukcję rygli z pofalowanymi środnikami na słupach żelbetowych.

Rys.3. Dźwigary z pofalowanym środnikiem na słupach żelbetowych [7]
Na rys. 4 pokazano system hal blachownicowych w systemie Astron (obecnie Lindab), złożoną z wieloprzęsłowych rygli i słupów- blachownic.

Rys.4. Hala blachownicowa w systemie ASTRON (LINDAB) [8]
Uwagi o ekonomiczności hal z ryglem pełnościennym
Hale z ryglami i/lub słupami pełnościennymi są szeroko stosowane we współczesnym budownictwie. Zużycie stali na na przekrycie hal z ryglami pełnościennymi jest nieco większe od hal z ryglami kratowymi (patrz rys.1 w artykule „Hale stalowe optymalne konstrukcyjnie „]). W przypadku układów poprzecznych pełnościennych możliwa jest pełna automatyzacja procesu wytwórczego, co zmniejsza koszty oraz czas produkcji hal i staja się one ekonomicznie konkurencyjne.
Coraz częściej hale, w których nie ma wymagań pożarowych (kategoria odporności ogniowej E) wykonuje się z kształtowników giętych na zimno (rozdz. 3.4.3. [1] -str.43)), [9].
Dla optymalnego rozstawu ram poprzecznych 6m, przekrycie wykonane z kształtowników z-g (zimno-giętych) jest ok ¼ lżejsze od przekrycia wykonanego z kształtowników g-w (gorąco-walcowanych). Na rys.5 w nawiasie podano strefy obciążeń klimatycznych, np. (1w/1ś) oznacza 1 strefę obciążenia wiatrem i 1-szą obciążenia śniegiem.
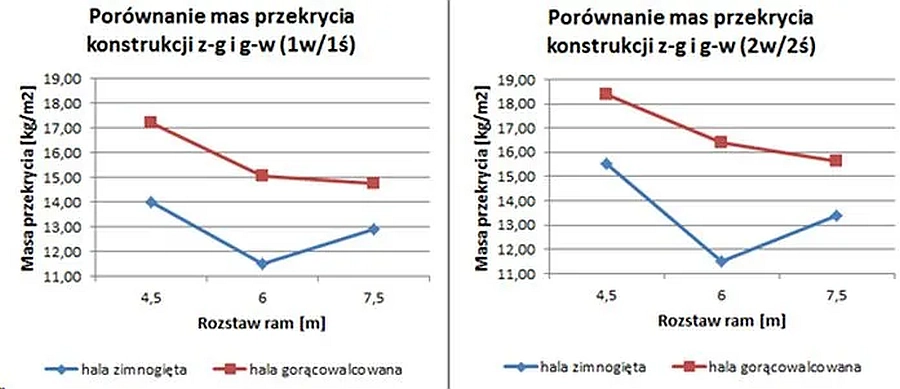
Rys.5 Porównanie mas przekrycia hali referencyjnej z kształtowników giętych na zimno i profili gorąco-walcowanych [9]
Dźwigary pełnościenne – blachownice
Charakterystyka blachownic
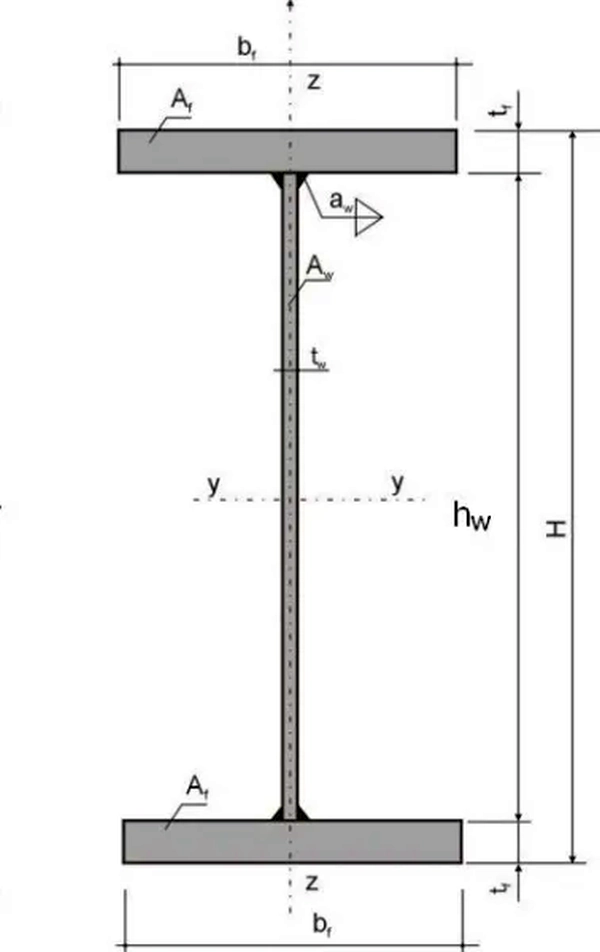
Podstawowym elementem hal pełnościennych są blachownice, czyli dźwigary spawane z blach, złożone z pasów i środnika- rys. 6 .
Blachownice są zdolne do przenoszenia większych obciążeń od standardowych kształtowników walcowanych , przede wszystkim ze względu na optymalne wysokości oraz żebrowania smukłych środników i są zwykle stosowane jako podciągi dużej rozpiętości w stropach budynków, dźwigary mostowe i w konstrukcjach przemysłowych. Najbardziej imponujące są nowoczesne zastopowania o rozpiętości ponad 200 m, o wysokości 5-10 m.
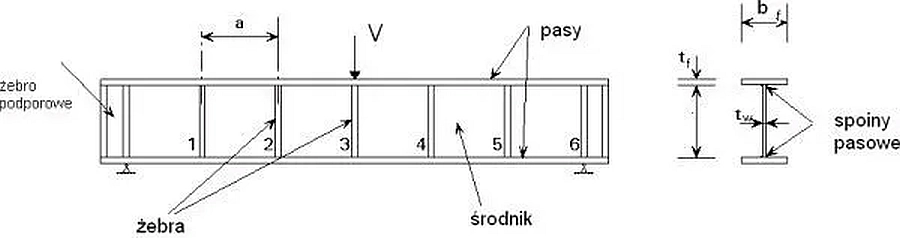
Takie dźwigary charakteryzuje duża smukłość środników i podatność na lokalne wyboczenia, oraz praca w zakresie pozakrytycznym, to znaczy uwzględnienie faktu, że po utracie stateczności środnika, cały dźwigar spełnia jeszcze warunki nośności. W celu zapewnienia stateczności smukłych, płaskich ścianek blachownice wyposażą się w użebrowanie środnika (rys.7, 8)
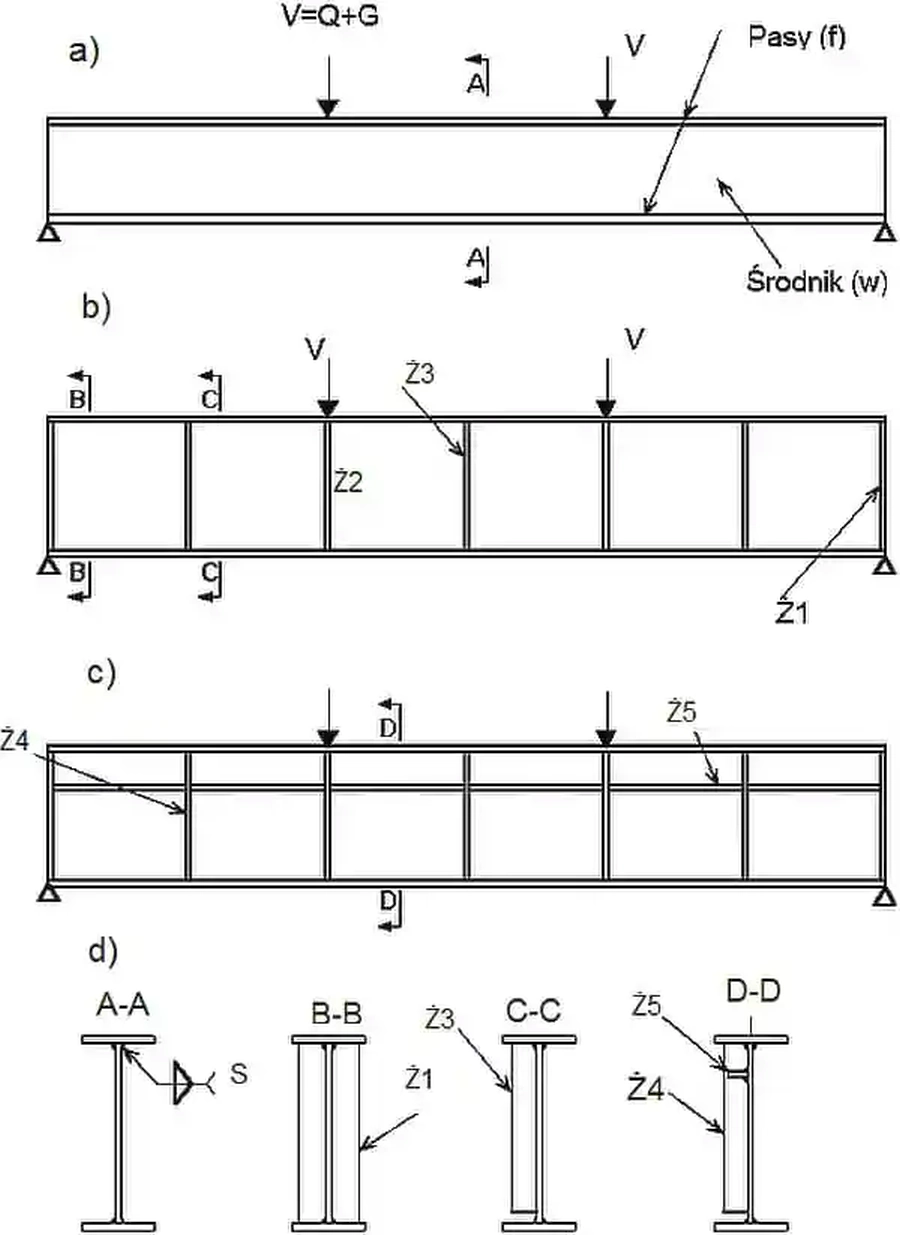
Rys.8. Elementy blachownic spawanych: a) bez żeberek, b) z żebrami poprzecznymi: Ż1- podporowe, Ż2- pod siłą skupioną, Ż3 – pośrednie , c) z żebrami poprzecznymi Ż4 i podłużnymi Ż5 (zmodyfikowane [10])
Charakterystyczna jest również zmienność przekroju po długości belki (rys.9), częste stosowanie przekrojów hybrydowych (pasy i środnik z innych stali), a także belek zespolonych z płytą żelbetową ( rys.10a ) oraz stosunkowo łatwe otworowanie wzmocnionego żebrami środnika w celu umieszczenia instalacji ( rys.10d ).
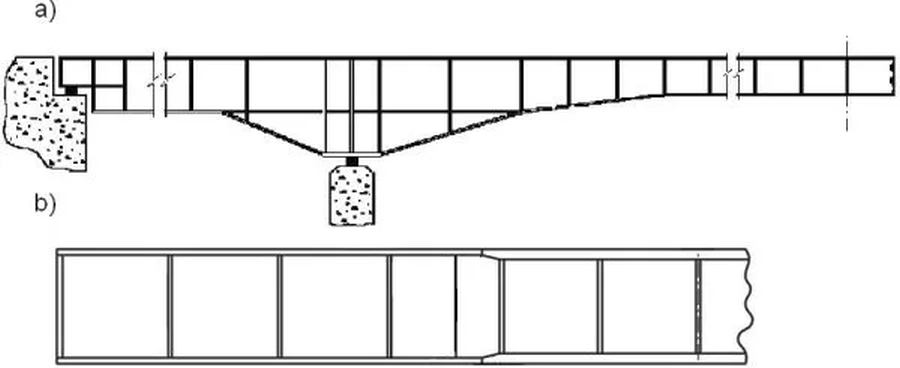
Rys.9. Zmiana przekroju blachownicy: a) poprzez zmianę wysokości środnika, b) poprzez zmianę grubości pasów (zmodyfikowane (zmodyfikowane [10])
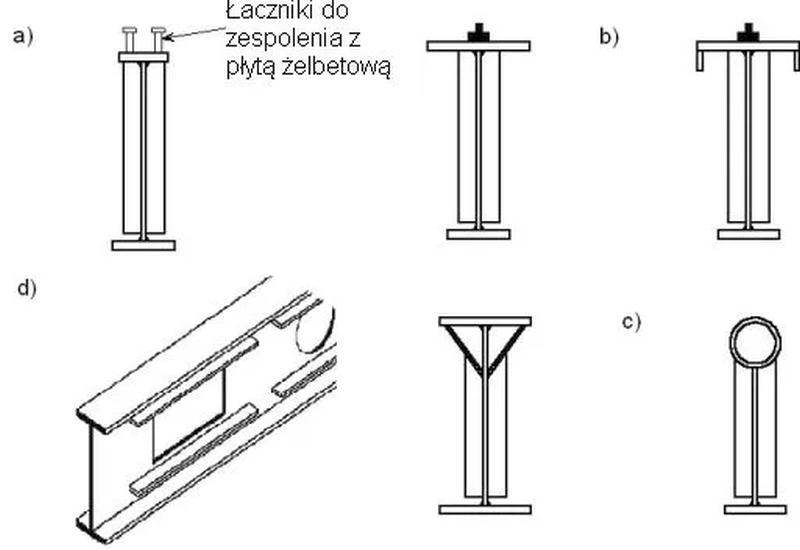
Rys.10. Typy blachownic: a) do zespolenia z płytą żelbetową, b) belki podsuwnicowe, c) rozmaite pasy górne, d) otwory na instalacje w środniku (zmodyfikowane [10])
Projektowanie blachownic
Wprowadzenie
Projektowanie belek blachownicach jest klasycznym przykładem optymalizacji wielokryterialnej (kryterium minimum zużycia stali, minimum liczby różnych elementów, minimum robocizny) i wieloczynnikowej ( parametrami projektowania są nie tylko wymiary przekrojów, ale również skokowy rozkład tych przekrojów na długości belki oraz rodzaj materiału). Ograniczenia optymalizacji blachownic często nie dają się ująć jednoznacznie, ponieważ muszą uwzględniać topologię i wymiary konstrukcji przylegających (np. belek stropowych), a także ograniczenia geometryczne obiektu. Występowanie takich ograniczeń i ich wartości ustala sie indywidualnie dla każdego obiektu.
W sytuacji wielowariantowości projektu blachownicy najskuteczniejszy okazuje się tradycyjny sposób optymalizacji polegający na iteracyjnym doborze jednego z parametrów projektowania, aż do spełnienia ograniczeń konstrukcyjnych oraz wytrzymałościowych. Pod obciążeniami statycznymi krytycznym elementem blachownicy jest środnik i jego smukłość, w tym w konieczności zapewnienia stateczności podczas montażu.
Pod doborze wymiarów blachownic należy przeprowadzić dopasowanie ich nośności do przebiegu sił przekrojowych. Zmianę nośności blachownicy uzyskuje się poprzez zmianę wymiarów przekroju po jej długości. Można różnicować wiele parametrów przekrojów: wymiary pasa lub wymiary środnika lub pas i środnik jednocześnie. W rezultacie można uzyska optymalny projekt belki.
Tok projektowania spawanych blachownic o zmiennych przekrojach można zawrzeć w następujących krokach:
1) dobór schematu statycznego blachownicy,
2) zestawienie obciążeń i dobór schematu obciążeń i obliczenia statyczne,
3) wstępny dobór przekrojów blachownicy,
4) dobór punktów zmiany przekroju blachownicy,
5) sprawdzenie warunków wytrzymałościowych,
6) sprawdzenie przemieszczeń,
7) sprawdzenie stateczności belki i jej elementów,
8) projekt żebrowania środnika,
9) projekt połączeń technologicznych i montażowych,
10) projekt naroży i innych elementów.
Schemat statyczny i obciążeń blachownicy. Obliczenia statyczne
Długości obliczeniowe przęseł belki blachownicowej wyznaczamy biorąc pod uwagę punkty podparcia (miejsca podpór). Punkty
podparcia przyjmujemy w następujący sposób:
1) jeśli belka oparta jest na podłożu (lub slupie) za pośrednictwem płytki lub łożyska centrującego – w punkcie wycentrowania,
2) jeśli belka oparta jest bezpośrednio na murze lub na wieńcu żelbetowym 2.5% odległości w świetle murów w głąb muru.
Blachownice są zwykle podparte na murze za pośrednictwem łożysk (obecnie elastomerowych) , a na głowicy slupów za pośrednictwem płytki centrującej.
W zestawieniu obciążeń należy wziąć pod uwagę wartości obciążeń stałych i zmiennych ze stosownymi współczynnikami obciążeń oraz redukcyjnymi. Obciążenia stałe, to najczęściej ciężar własny stropu. Obciążenia zmienne, to najczęściej ciężar ludzi maszyn i sprzętu na stropach. Obciążenie użytkowe stropu $Q$ oraz obciążenie stale $G$ przekazują się na blachownice w większości w postaci sil skupionych z belek stropowych. Natomiast ciężar własny blachownicy jest obciążeniem rozłożonym. Rozsądnie jest przyjąć, ze całe obciążenie oprócz ciężaru własnego składa się z sił skupionych przyłożonych w miejscu połączenia z belkami stropowymi. Założenie takie może prowadzić do niewielkiego przeszacowania sil przekrojowych w stosunku do sił wywołanych rzeczywistymi obciążeniami. Ciężar własny $ g \, [kN/m]$ jednego metra blachownicy o długości L [m] najdłuższego przęsła można wstępnie oszacować z zależności $(\ref{1})$, ustalonej na podstawie projektów wielu zrealizowanych blachownic:
$$ \begin{equation} g=0,85(0,7 +0,1\cdot L) \label{1} \end{equation}$$
Obciążenie stale G działa na wszystkie przęsła, a obciążenie zmienne Q może działać tylko na niektórych przęsłach(np na rys. 12b pokazano obciązenie Q na 1-szym przęśle.
W przypadku belki n-przęsłowej liczba wszystkich możliwych schematów obciążeń $n_{schemat}$ wynosi:
$$ \begin{equation} n_{schemat}=2^n \label{2} \end{equation}$$
Na przykład dla belki 2-przęsłowej, pokazanej na rys. 12 mamy $2^2=4$ schematy= { 0 , 1 , 2 , 1+2}.
Spośród możliwych schematów obciążeń można wybrać do obliczeń tylko niektóre maksymalizujące siły przekrojowe w wybranych miejscach belki. W przypadku stosowania programów obliczeniowych wymagane są sprawdzenia wyrywkowe dla najbardziej niekorzystnych schematów oraz miejsc na blachownicy – inżynier nie powinien zdawać się w pełni na rozwiązania maszyny.
Zalecenia konstrukcyjne
Zalecenia konstrukcyjne dotyczą proporcji wymiarowych przekroju blachownicy, których zachowanie najczęściej zapewnia optymalne zużycie stali.
Wymiary środnika
Najczęściej przyjmuje się stałe po długości wymiary środnika $h_w$ i $t_w$.
Z doświadczenia wynika, że dla belek o długości maksymalnego przęsła $L$, w których ograniczono ugięcia do $\cfrac{L}{250}$ wysokość środnika $h_w$ można wstępnie oszacować z warunków :
$$\begin{equation} h_w = \begin {cases}
\left( \cfrac{1}{10} \div \cfrac{1}{20} \right ) \cdot L & \textrm { dla belki wolnopodpartej} \\
\left( \cfrac{1}{16} \div \cfrac{1}{30}) \right) \cdot L & \textrm { dla belki ciągłej} \\
\end {cases} \label{3}\end{equation}$$
Z zadania minimalizacji masy przekroju otrzymujemy warunek:
$$\begin{equation} h_w \approx \alpha \cdot \sqrt{ \cfrac{M_{Ed,max}} { f_y / \gamma_{M0} \cdot t_w} } \label{4} \end{equation}$$
gdzie:
$M_{Ed,max}$ – maksymalny po długości belki moment zginający przekrój. wywołany obciążeniami obliczeniowymi ,
$f_y $ – granica plastyczności stali (dla przekrojów hybrydowych dla pasów), $\gamma_{M0}=1.0 $ – współczynnik materiałowy stosowany przy sprawdzaniu nośności przekroju.
$\alpha$- współczynnik $=1,1$ dla belek o stałym przekroju w przęśle , $= 1,0$ dla belek o zmiennym przekroju.
Do wstępnych szacunków najczęściej przyjmuje się $ t_w \approx\cfrac {h_w}{100}$ lub $t_w \approx 7+ \cfrac{3 \cdot h_w}{1000}$.
Grubość środnika $t_w$ przyjmuje się wstępnie z warunków:
$$\begin{equation} t_w \begin {cases}
= \left( \cfrac{1}{90} \div \cfrac{1}{160} \right) \cdot h_w \\
\ge 7 \, mm & \textrm{ dla belek narażonych na wpływy atmosferyczne} \\
\ge 6 \,mm & \textrm{ dla belek nie narażonych na wpływy atmosferyczne} \\
\le 40 (30) \, mm & \textrm{ ze względu na ciągliwość międzywarstwową – stal S235 (S355) } \\
\end {cases} \label{5} \end{equation}$$
Dla znanych długości efektywnych przęseł belki $L_{ei}$ , to znaczy odległości pomiędzy punktami zerowania się momentów zginających, wysokośc blachownicy sprawdza się z warunku $(\ref{3})$ dla $L= max \{ L_{ei} \}$. W przypadku rygorystycznych wymogów dla granicznych ugięć należy przyjmować górne granice wysokości środnika.
Wymiary pasa
Szerokości pasów $b_f$ przyjmuje się w proporcjach
$$\begin{equation} b_f \begin {cases}
= \left( \cfrac {1}{3} \div \cfrac {1}{5} \right) \cdot h_w \approx \cfrac{1}{4} h_w \\
\ge 80 \, mm \\
\end {cases} \label{6} \end{equation}$$
Grubość pasów $t_f$:
$$\begin{equation} \begin {cases}
t_w+1 < t_f < 3,5 t_w \\
t_f \le 30 \, mm & \textrm { dla stali S355} \\
$t_f \le40 \, mm & \textrm {dla stali S235}
\end {cases} \label{7} \end{equation}$$
Pole przekroju pasa $A_f=b_f \cdot t_f$ można wyznaczyć z przybliżonej zależności wytrzymałościowej:
$$\begin{equation} A_f \ge \cfrac {M_{Ed}}{\chi \cdot f_{yt}(h_w-t_f) \gamma_{M0}} \label{8} \end{equation}$$
gdzie współczynnik wyboczenia bocznego $\chi=1,0$ dla belek zabezpieczonych przed zwichrzeniem.
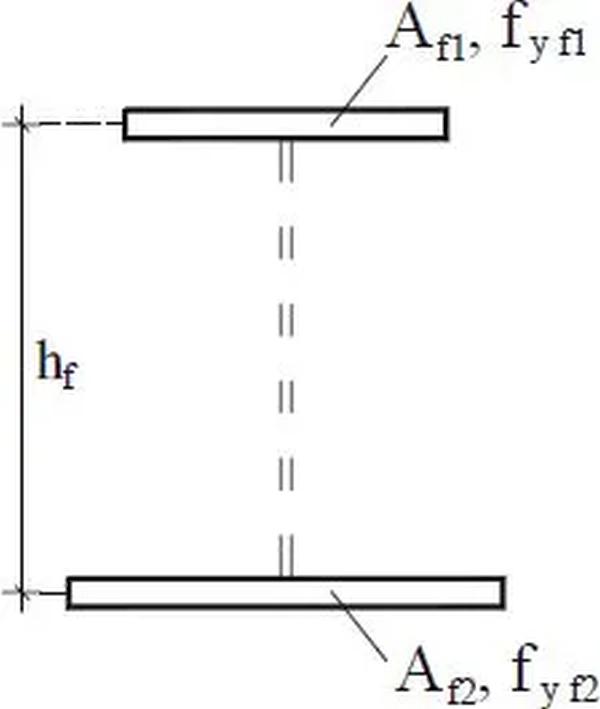
Formułę $(\ref{9})$ uzyskano po potraktowaniu przekroju blachownicy jako przekroju dwupunktowego (przekrój sandwich złożony z dwóch pasów bez środnika (rys.11)
Dla przekroju blachownicy (rys.6) z hybrydowymi pasami mamy nośność:
$$\begin{equation} M_{f,Rd} = min \left [h_f \cdot A_{f1}\cdot \cfrac{f_{53}}{\gamma_{M0}}, h_f \cdot A_{f2}\cdot \cfrac{f_{54}}{\gamma_{M0}} \right ]\label{9} \end{equation}$$
Pas powinien spełniać warunki dla ścianki klasy 3 zgodnie z tabl. 5.2. [11], czyli tak aby ścianka pasa nie uległa utracie stateczności miejscowej:
$$\begin{equation} \lambda_f= \cfrac{c_f}{t_f}\le 14 \varepsilon \label{10} \end{equation}$$
gdzie: wysięg ścianki pasa $c_f= \cfrac{b_f-t_w-2 a_s}{2}$; $ a_s $ – grubość spoiny pasowej; $\varepsilon = \sqrt { \frac{235}{f_y}}$.
Przesunięcie $c$ praktycznego punktu zmiany sztywności i odsunięcie od żeber
Odsunięcie praktycznego punktu zmiany sztywności blachownicy w stosunku do punktu teoretycznego w kierunku mniejszego
wytężenia (zmniejszających się sił przekrojowych) przyjmuje się:
$$\begin{equation} c \ge \cfrac {b_f}{2} \label{11} \end{equation}$$
Ze względów technologiczno-konstrukcyjnych punkt zmiany sztywności powinien być odsunięty od żeber lub podpór o $c$
$$\begin{equation} c \ge \label{12} \begin {cases}
1 \, m & \text{od podpory}\\
200 \, mm \, i \, 20 \cdot t_w & \text{ od lica żeberka}
\end {cases} \end{equation}$$
W przypadku styku spawanego pasa o różnych grubościach, należy go sytuować blisko żebra w odległości
$$\begin{equation} c \ge \begin {cases}
200 \, mm\\
\cfrac {b_0}{2} \text{ od osi żebra poprzecznego}
\end {cases} \label{13} \end{equation}$$
gdzie $b_0$ jest odległością między żebrami podłużnymi, które w blachownicy bez żeber podłużnych $b_o=h_w$.
Długości $l_1$ odcinków blachownicy i liczba różnych przekroi
Ze względów technologiczno-ekonomicznych oraz konieczności typizacji przyjmuje się następujące ograniczenia:
Minimalna długość elementu blachownicy i nakładki na pas $l_1$
$$\begin{equation} l_1 \ge 2 \, m \label{14} \end{equation}$$
Liczba różnych przekroi na całej belce $n_b$ i w przęśle $n_1$
$$\begin{equation} \begin {cases}
n_b \le 6 \\
n_1 \le 4
\end {cases} \label{15} \end{equation}$$
Kształtowanie blachownicy po długości
Zmianę przekrojów blachownicy dokonujemy z warunku dostosowania nośności belki do obwiedni sił przekrojowych. Zmianę sztywności blachownicy można uzyskać przez zmianę wymiarów środnika i/lub zmianę wymiarów pasów. W konstrukcjach budowlanych najczęściej dokonuje się zmiany grubości pasa t przy stałych wymiarach $h_w, t_w, b_f$.
Nad podporami środkowymi zwiększa się w niektórych przypadkach wysokość środnika (rys.9). Ten zabieg należy skonfrontować z wymogami stateczności miejscowej.
Zmiany tylko grubości $t_f$ przy stałej szerokości pasa umożliwiają zastosowanie belek stropowych jednego typu. Przy pominięciu sił poprzecznych, teoretyczne punkty zmiany przekroju można wyznaczyć, jako punkty przecięcia obwiedni momentów zginających z obwiednią nośności. Obliczeniową nośność przekroju i-tego $M_{Ri}$ mierzoną czystym momentem zginającym można wyznaczyć ze wzoru:
$$\begin{equation} M_{Ri}=W_i \cdot \frac {f_y}{\gamma_{m0}} \label{16} \end{equation}$$
gdzie: wskaźnik wytrzymałości przekroju $W_i= \cfrac {I_i}{(\frac {h_w}{2}+t_f)}$,
$ I_i$ – moment bezładności przekroju i-tego względem osi $y$, $f_y$ – granica plastyczności stali, $\gamma_{m0}=1$ – częściowy współczynnik bezpieczeństwa (materiałowy) przyjmowany przy sprawdzaniu nośności przekroju.
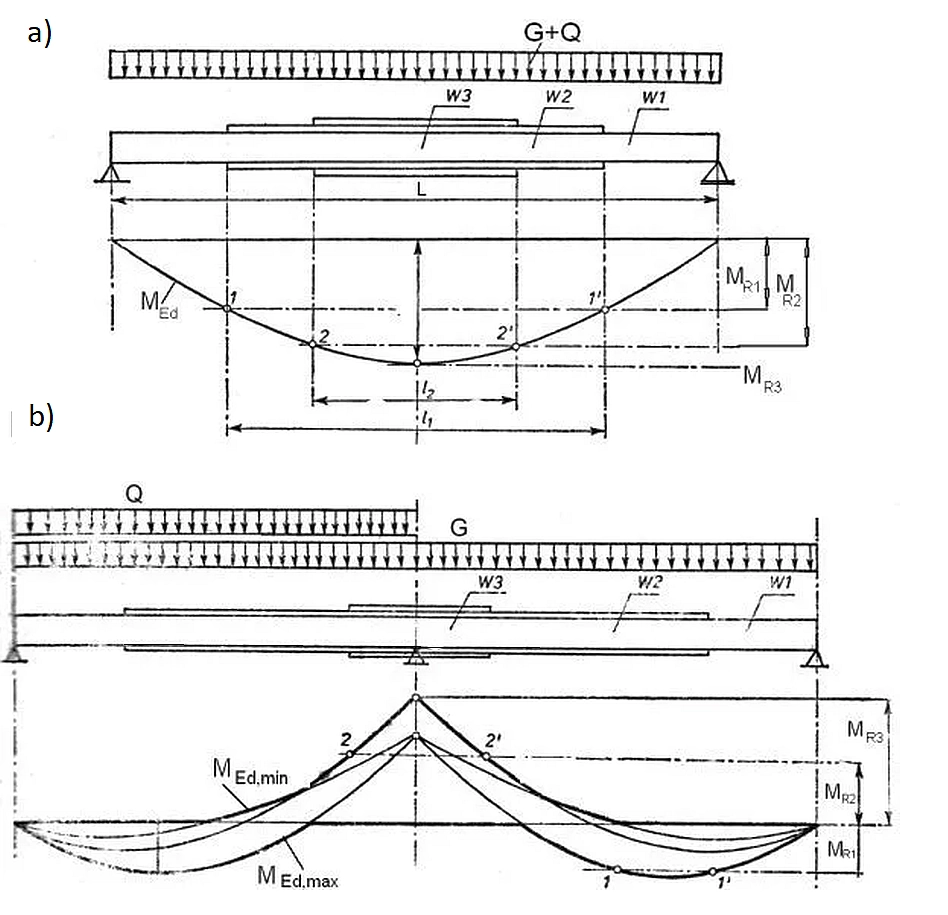
Rys. 12 Graficzne kształtowanie blachownicy po długości: a) jednoprzęsłowej, b) ciągłej, dwuprzęsłowej: Wi – elementy (odcinki blachownicy) o nośności MRi (zmodyfikowane [12])
Nad podporą pośrednią nad belką (rys 12b) lub słupem (rys. 13) o skończonej, rzeczywistej szerokości $b$ następuje ścięcie „ząbka” teoretycznego momentu zginającego $M$, co szacujemy w sposób pokazany na rys. 13c. z następującej zależności:
$$\begin{equation} p=\cfrac{V}{b} \to \Delta M= p \cdot \cfrac {b}{2}\cdot \cfrac{b}{4}=p \cfrac{b^2}{8}= \cfrac{V b}{8} \label{17} \end{equation}$$
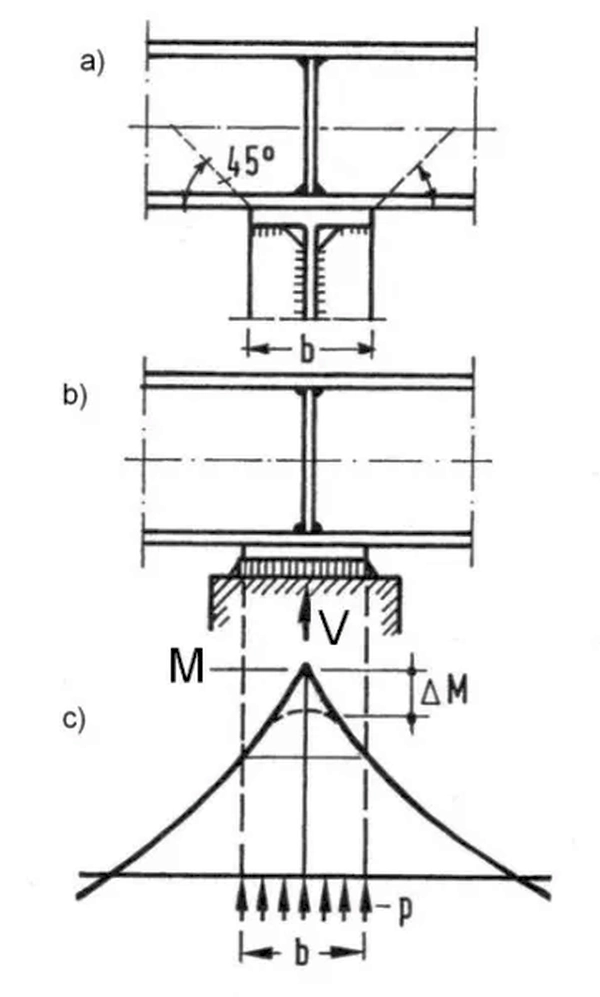
Rys. 13 Ścięcie $\Delta M$ momentu zginającego $M$ nad podporą pośrednią [13]-str. 724
Wstępny dobór punktów zmiany przekroju blachownicy możemy dokonać graficznie poprzez dopasowanie obwiedni nośności $M_{Rd}$ do obwiedni momentów zginających $M_{Ed}$.
W przypadku belki wolnopodpartej kształtowanie blachownicy przedstawiono na rys. 12a podstawowy przekrój blachownicy W1 ma nośność ($\ref{16{$) $M_{R1}$ i przecina wykres momentów zginających $M_{Ed}$ w punkcie $1$ oraz $1’$. Punkty te są teoretycznymi punktami zmiany przekroju, w których należy zwiększyć przekrój do W2 o nośności $M_{R2}$ na przykład poprzez zmianę grubości pasa $t_{f2} > t_{f1}$.
W praktyce zmianę przekroju należy dokonać w pewnej odległości $c$ od punktu teoretycznego w kierunku mniejszych momentów zginających. Przesunięcie to należy wyznaczyć uwzględniając działanie sił poprzecznych oraz osłabienie przekroju łącznikami. Zaleca się, aby przesuniecie $c \approx \cfrac{b_f}{2}$.
W przypadku belek ciągłych dobór zmiany przekrojów po długości powinien uwzględniać obwiednie momentów zginających: momenty minimalne $M_{Ed, min}$ oraz maksymalne $M_{Ed,max}$ (rys, 12b) dla wszystkich możliwych schematów obciążeń. Przekrój podstawowy W1 można teoretycznie zastosować do punktu $1’$, a dalej aż do punktu $2’$ dajemy przekrój W2. Na odcinku maksymalnych momentów zginających stosujemy przekrój W3. Przy tym wstępny dobór przekroju W3 powinien przewidywać to, że nad podporą działają znaczne siły poprzeczne i przekrój blachownicy powinien mieć rezerwy – zalecamy, by wstępnie powiększyć nośność czystego zginania o ok 20%.
Liczbę zmian przekrojów blachownicy przyjmuje się w taki sposób, aby na całej długości blachownicy nie było zbyt wiele różnych przekrojów (zwykle max 6), a także, aby długości poszczególnych odcinków pasów nie były mniejsze od ustalonej wartości, którą zwykle przyjmuje się równą 2 m. Punkty zmian przekroju nie powinny być przyjmowane zbyt blisko podpór (orientacyjnie dalej niż 1 m od podpory) i nie powinny wypadać zbyt blisko żeber (orientacyjnie dalej niż i 30 cm od żeberka). Na długości jednego prześlą liczba zmian przekroju nie powinna przekraczać 4, a liczba różnych przekrojów na całej belce nie powinna być większa od 6.
Na rys. 14a pokazano linie naprężeń w pasie górnym wykonanym z grubej blachy. Ze względu na niekorzystną pracę grubych blach zaleca się, by w potrzebie stosowania grubych pasów , wykonywać je z pakietu blach , w sposób pokazany na rys. 14b do e).
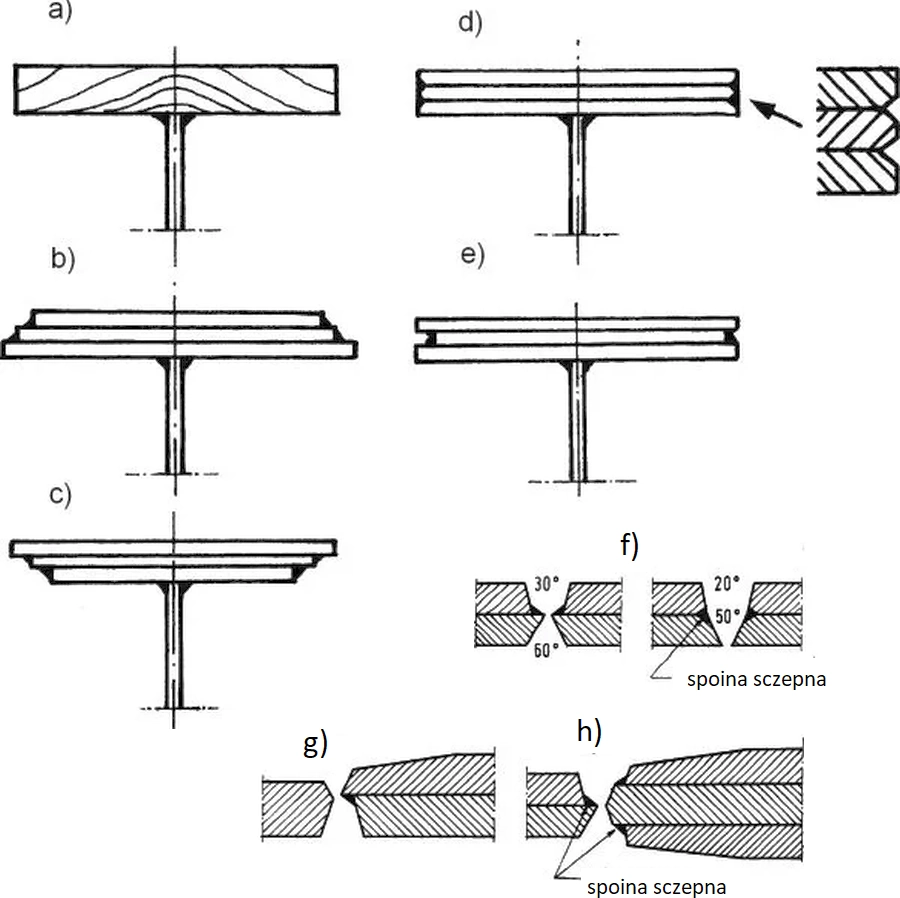 Rys. 14. Sposoby łączenia, ukosowaniai spawania pakietu blach pasa [13]-str. 720
Rys. 14. Sposoby łączenia, ukosowaniai spawania pakietu blach pasa [13]-str. 720
Spoiny łączące pakiet powinny być dobrej jakości, co łatwiej uzyskać w przypadku 14b) (spoiny podolne) niż14c). Dla przypadku 14d) należy stosować brzegi blach do ułożenia spoin rowkowych. Na rys. 14 f,g,h pokazano sposoby ukosowania i podpawania blach pakietu.
W celu oszacowania odcinka pasa $l_0$ na którym można zastosować przekrój o nośności $M_R=M_0$ można skorzystać z zależności $(\ref{18})$:
$$\begin{equation} l_0= l \cdot \sqrt{1 – \cfrac{M_0}{M}} \label{18} \end{equation}$$
gdzie: L- jest odległością pomiędzy miejscami zerowymi wykresu momentów zginających przęsła belki obciążonej zastępczym obciążeniem równomiernym z maksymalną, wywołującym maksymalny moment zginającym $M$. Dla belki swobodnie podpartej zobrazowano to na rys.15. Długość $L=L_e$ zgodnie z rys. 16.
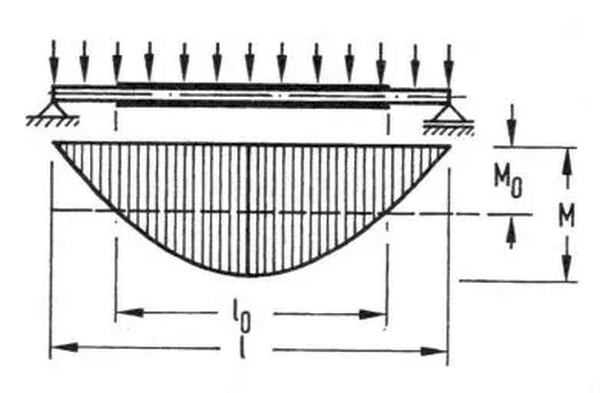
Rys.15 Szacowanie długości pasa (nakładki) [13]-str. 720
Weryfikacja projektu blachownicy
Blachownica zaprojektowana zgodnie z zasadami opisanymi wyżej powinna zostać zobrazowana na rysunkach ze szczególnym uwzględnieniem współdziałania z elementami dochodzącymi oraz spełnienia funkcji do jakiej jest przeznaczona. Taki projekt zasadniczy podlega weryfikacji pod względem spełnienia wymogów szczegółowych.
W zakresie konstrukcyjnym należy dokonać weryfikacji obliczeniowej, przy czym należy odróżnić projekt od obliczeń statyczno- wytrzymałościowych, które stanowią czynności pomocnicze do wykonania projektu zasadniczego, a po jego zakończeniu służą wyłącznie do weryfikacji przyjętych rozwiązań i powinny w zasadzie potwierdzać przyjętą koncepcję i projekt. Jeśli weryfikacja wykaże konieczność istotnych modyfikacji, to będzie to oznaczało, że projekt zasadniczy nie został wykonany poprawnie i nie najlepiej świadczy o inżynierze, który go wykonał. Drobne modyfikacje są natomiast normalne i przebiegają w procesie iteracyjnym aż do momentu, by wszystkie uwarunkowania w tym trwałość i niezawodność elementów została osiągnięta.
Ze względu na złożone formuły analityczne sprawdzenie projektu dokonuje się za pomocą programów lub Arkuszów obliczeniowych. W kolejnych punktach wypisano najważniejsze formuły i przybliżono rysunek teoretyczny w celu zilustrowania problemu, ale bez zakładania, że inżynier będzie te formuły wykorzystywał w obliczeniach ręcznych.
Projekt podstawowy powinien zostać uzupełniony o rozwiązania szczegółowe połączeń z otaczającymi elementami budowlanymi (np. podłączenia belek stropowych, łożyska), a także pomiędzy elementami wysyłkowymi blachownicy (połączenia technologiczne – montażowe). Współcześnie w związku z wyraźnymi rozdzieleniem roli Projektanta i Wykonawcy, dokumentację podziału na elementy wysyłkowe oraz połączeń technologicznych (styków montażowych) opracowuje Wykonawca i przestawia Projektantowi do zatwierdzenia.
Efekt szerokiego pasa
W przypadku zastosowania szerokich pasów blachownic $b_f$ (p. rys.6) wystąpi w nich nierównomierny rozkład naprężeń normalnych, co zgodnie z normą [14], kl. 3.1.(1) należy uwzględnić w obliczeniach, jeśli zajdzie warunek
$$\begin{equation} b_0 > \cfrac{L_e} {50} \label{19} \end{equation}$$
gdzie:
$b_o= \cfrac{b_f-t_w}{2}$ – szerokość wystającej (wspornikowej) części pasa lub połowa szerokości części przęsłowej (dwustronnie podpartej),
$L_e$ – odległość między punktami zerowych momentów zginających wg rys. 16.
Jeśli warunek $$\ref{19}$) nie jest spełniony, to efekt szerokiego pasa można pominąć. Z analizy zrealizowanych obiektów wynika, że optymalne projekty blachownic uzyskuje się wówczas, gdy efekt szerokiego pasa nie wystąpi.
Długość efektywna belki $L_e$ jest odległością pomiędzy punktami zerowego momentu zginającego. W przypadku, gdy długości przęseł nie różnią się więcej niż o 50%, a ewentualny wspornik nie przekracza połowy przęsła sąsiedniego, to można korzystać z rys. 16a. W tym przypadku mamy:
dla przęsła skrajnego $L_e=0,85L$,
dla przęsła pośredniego $L_e=0,70 L$,
nad podporą $L_e=0,25(L+L)=0,5 L$.
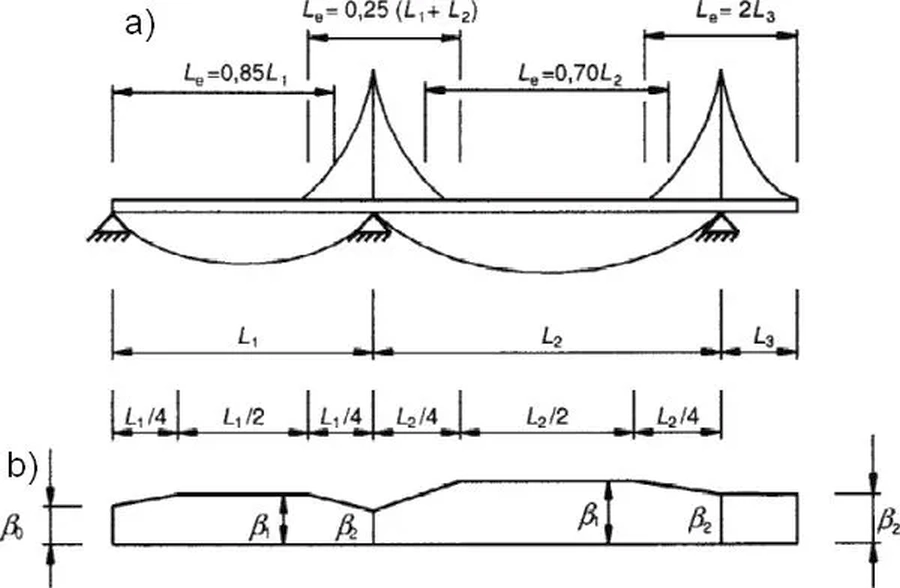
Rys. 16. Sposób wyznaczania efektu szerokiego pasa: a) długości efektywne, b) współczynniki szerokości efektywnej [14] – rys.3.1
Dla $L_e=0,85L$ z $(\ref{19})$ otrzymujemy wartość graniczną:
$$\begin{equation} b_{lim} \approx \cfrac{L}{30} \label{20} \end{equation}$$
W przypadku zaprojektowania przekroju zgodnie z zaleceniami ($b_f= \frac{1}{4} h_w$ – nawet dla $h_w=\frac{L}{10}$ mamy $b_f =\frac{L}{40}$, czyli pas jest węższy od wartości granicznej i wówczas efekt szerokiego pasa można pominąć.
Jeśli warunek $( \ref{20})$ nie jest spełniony w danym przęśle, to efekt szerokiego pasa należy uwzględnić w tym przęśle po spełnieniu warunków normy [14], kl. 3, a w szczególności stan graniczny nośności należy sprawdzać z postanowieniami [14], kl. 3.3.
W niniejszym artykule zajmujemy się optymalnymi blachownicami, w których nie wystąpi efekt szerokiego pasa.
Przekroje, w których należy sprawdzić nośność blachownicy
Nośność przekroju blachownicy winna być sprawdzona w przekrojach krytycznych:
1) w miejscu skoku sił : pod każdą silą siłą skupioną ( w tym nad podporami),
2) w punktach ekstremów lokalnych sił przekrojowych (M, V, N),
3) w punktach zmiany sztywności blachownicy (zmiany przekroju).
Proste zginanie
Nośność przekroju w licu żeber w przekrojach wyżej wskazanych powinna być sprawdzona z podstawowego warunku prostego zginania (nośność plastyczna bez uwzględnienia stateczności):
$$\begin{equation} M_{Ri} \le M_{Edi} \label{21} \end{equation}$$
gdzie:
$M_{Edi}$ – obliczeniowy moment zginający przekrój i-ty,
$M_{Ri}=M_{pl,Rd}$ – obliczeniowa nośność przy zginaniu, traktowana jako nośność plastyczna przekroju złożonego z efektywnych części pasów oraz w pełni efektywnego środnika, niezależnie od jego klasy przekroju [14]), kl. 7.1 (1).
Sprawdzenie ($\ref{21}$) należy traktować jako wstępne tylko na dominującą siłę przekrojową. Przekroje w odległości $\frac{h_w}{2}$ od podpór i w odległości $15 t_w$ od innych żeber lub w miejscach dużych sił poprzecznych poza obszarem stosowania żeber należy sprawdzić na współdziałanie zginania i ścinania zgodnie z rozdziałem Interakcja zginania i ścinania.
Proste ścinanie
Warunek nośności przekroju ścinanego siłą $V_{Ed}$ ma postać – przekształcona zależność [14], wzór (5.10):
$$\begin{equation} V_{Ed} \le V_{b,Rd} \label{22} \end{equation}$$
gdzie:
nośność przekroju na ścinanie $V_{b,Rd}$ wyznacza się jako sumę nośności środnika $V_{bw,Rd}$ i pasów $V_{bf,Rd}$ z ograniczeniem do $V_{b,Rd,lim}$ jak następuje[14], wzór (5.1):
$$\begin{equation} V_{b,Rd}=V_{bw,Rd}+ V_{bf,Rd} \le V_{b,Rd,lim} \label{23} \end{equation}$$
Udział pasów w nośności przekroju na ścinanie uwzględnia się tylko wówczas, gdy pas ma zapasy nośności przy zginaniu, tzn, gdy:
$$\begin{equation} M_{f,Rd} > M_{Ed} \label{24} \end{equation}$$
gdzie: $M_{f,RD}$ – obliczeniowa nośność przy zginaniu przekroju złożonego wyłącznie z efektywnych pasów (przekrój sandwich – rys.11 ), którą dla dwuteownika symetrycznego ($A_{f1}=A_{f2}$) i pasów klasy 3, wykonanych z takiej samej stali ($f_{53}=f_{54}=f_{yf}$),należy wyznaczać z formuły
$$\begin{equation} M_{f,Rd} = b_f \cdot t_f \cdot h_f\cdot f_{yf} \label{25} \end{equation}$$
gdzie: $h_f = h_w+t_f$
Ograniczenie górne nośności na ścinanie ($\ref{23}$) wynosi:
$$\begin{equation} V_{b,Rd,lim}= \cfrac{\eta f_{yw} h_w t_w}{\sqrt {3} \gamma_{M1}} \label{26} \end{equation}$$
Parametr $\eta$ przyjmuje wartości:
$$\begin{equation} \eta= \begin {cases}
1,20 & \text{ dla stali gatunków nie lepszych od S460} \\
1,00 & \text { dla stali gatunków powyżej S460}
\end {cases} \label{27} \end{equation}$$
gdzie:
$f_{yw}$ – granica plastyczności stali środnika,
$\gamma_{M1}=1,0$ – współczynnik materiałowy przy sprawdzaniu elementów przekroju.
Udział pasów w nośności na ścinanie, wyznaczony z teorii nośności granicznej można zapisać w postaci [14], wzór (5.8):
$$\begin{equation} V_{b,f,Rd}= \cfrac{b_f \cdot t_f^2 \cdot f_{yf}}{c\cdot \gamma_{M1}} \left [ 1- \left (\cfrac{M_{Ed}}{M_{f,Rd}} \right)^2 \right] \label{28} \end{equation}$$
gdzie: $b_f$ i $t_f$ – wymiary pasa o mniejszej nośności na rozciąganie, przy czym $b_f$ jest szerokością efektywną pasa, ograniczoną z każdej strony środnika do wartości $15\varepsilon t_f$,
$ c= a \cdot \left ( 0,25+\cfrac{1,6 \cdot b_f \cdot t_f^2 \cdot f_{yf}}{t_w \cdot h_w^2 \cdot f_{yw}}\right ) $ – odległość przegubu plastycznego w pasie od żebra,
$a$ -szerokość pola miedzy żebrami poprzecznymi.
Udział środnika w nośności obliczeniowej na ścinanie wynosi [14], wzór (5.2):
$$\begin{equation} V_{bw,Rd}=\cfrac{\chi_w f_{yw}h_w t_w}{\sqrt{3} \gamma_{M1}} \label{29} \end{equation}$$
Współczynnik niestateczności przy ścinaniu środnika $\chi_w$ w przypadku środników użebrowanych przynajmniej na podporach można przyjmować wg rys. 17 dla smukłości względnej środnika
$$\begin{equation} \overline \lambda_w= 0,76 \sqrt{\cfrac{f_{yw}}{\tau_{cr}}} \label{30} \end{equation}$$
gdzie:
$$\begin{equation} \tau_{cr}= k_\tau \cdot \sigma_E \label{31} \end{equation}$$
$$\begin{equation} \sigma_E= \cfrac{\pi^2 \cdot E\cdot t_w^2}{12(\nu \cdot h_w^2}=190000(\cfrac{t_w}{h_2})^2 [MPa]\label{32} \end{equation}$$
$k_\tau$ – minimalny parametr niestateczności panelu środnika przy ścinaniu, zależny od sposobu użebrowaniu środnika.
Procedura wyznaczenia $min k_\tau$ jest złożona i opisana w [14], kl. 5.3(3) i (4) .
Gdy żebra poprzeczne występują wyłącznie na podporach, to [14], (wzór 5.5 ) :
$$\begin{equation} \overline \lambda_w=\cfrac{h_w}{86,4 t_w \varepsilon} \label{33} \end{equation}$$
Gdy oprócz żeber na podporach występują pośrednie żebra poprzeczne, żebra podłużne lub obu rodzajów, to [14], wzór (5.6 )
$$\begin{equation} \overline\lambda_w=\cfrac{h_w}{37,4 t_w \varepsilon} \sqrt{k_\tau} \label{34} \end{equation}$$
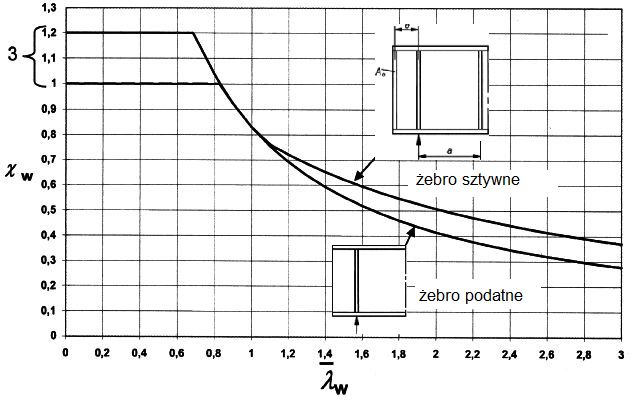 Rys.17. Współczynnik niestateczności środnika (zmodyfikowany rys. 5.2. [14]
Rys.17. Współczynnik niestateczności środnika (zmodyfikowany rys. 5.2. [14]
Formuły analityczne na współczynniki niestateczności przy ścinaniu środników zobrazowane na rys.17, są następujące:
$$\begin{equation} \chi_w=\begin {cases}
\eta & \text{ dla $ \overline \lambda_w < \cfrac{0,83}{\eta} $} \\
\cfrac{0,83}{\overline \lambda_w} & \text{ dla $ \cfrac{0,83}{\eta} \le \overline \lambda_w <1,08 $}\\
\cfrac {1,37}{0,7+\overline \lambda_w} & \text{ dla sztywnego żebra podporowego i $\overline \lambda_w \ge 1,08$}\\
\cfrac{0,83}{\overline \lambda_w} & \text{ dla podatnego żebra podporowego i $\overline \lambda_w\ge 1,08$}\\
\end {cases} \label{35} \end{equation}$$
gdzie $\eta$ wg $(\ref{27})$.
Nośność środnika pod siłą skupioną
Warunek nośności środnika przy obciążeniu poprzeczną siłą skupioną ma postać [14], wzór (6,14):
$$\begin{equation} \cfrac{F_{Ed}}{F_{b,Rd}} \le 1,0\label{36} \end{equation}$$
gdzie: $F_{Ed}$ – obliczeniowa siła skupiona, $F_{b,Rd}$ – obliczeniowa nośność pod siłą skupioną.
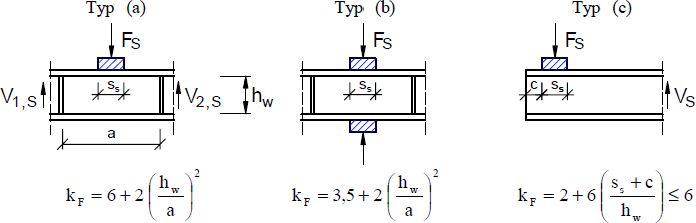
Nośność środnika pod siłą skupioną $F_{b,Rd}$ wyznacza się przy założeniu, ze pas ściskany (najczęściej górny) jest stężony w kierunku bocznym, czyli w sytuacji, gdy blachownica nie ulegnie zwichrzeniu (tab.1, poz. 2). Na rys. 18 przedstawiono rozpatrywane typy obciążenia:
- obciążenie przyłożone do pasa przenoszone prze siły poprzeczne w środniku ( typ a),
- obciążenie samozrównoważone – obustronne ściskanie środnika ( typ b),
- obciążenie pasa przy nieużebrowanym końcu elementu wspornikowego ( typ c).
Rys. 18 Parametry niestateczności dla różnych typów obciążenia [14]
Obliczeniową nośność środnika z żebrem lub bez żeber, ze względu na niestateczność pod siłą skupioną, wyznacza się z formuły [14], wzór (6,1)::
$$\begin{equation} F_{b,Rd}= \cfrac{{f_yw }L_{eff} t_w}{\gamma_{M1}} \label{37} \end{equation}$$
gdzie:
efektywna długość środnika przy obciążeniu skupionym $L_{eff}=\chi_F \lambda_y$,
współczynnik wyboczenia przy obciążeniu skupionym $\chi_F= \cfrac {0,5}{\overline \lambda_F}<1.0 $,
smukłość względna środnika przy obciążeniu skupionym $\overline\lambda_F= \sqrt{\cfrac{\lambda_y t_w f_{yw}}{F_{cr}}}$,
siła krytyczna skupiona $F_{cr}=0,9 \cdot k_F \cdot E \cfrac{t_w^3}{h_w},
parametr niestateczności $k_F$ wg rys.18.
Smukłość $\lambda_y$ wyznacza się z zależności[14], wzór (6,10) do (6.13) :
$$\begin{equation} \lambda_y= \begin {cases}
s_s+2t_f (1+\sqrt{m_1+m_2}) \le a & \text{ przy obciążeniu typu a) i b) } \\
\lambda_e +t_f \cdot min \{ \sqrt{\frac{m_1}{2}+(\frac{\lambda_e}{t_f})^2+m_2}; \sqrt{m_1+m_2} \} & \text{ przy obciążeniu typu c) }\\
\end {cases} \label{38} \end{equation}$$
gdzie $\lambda_e=\cfrac{k_F \cdot E t_w^2}{2 f_{yw}h_w}\le s_s+c$
Interakcja zginania i ścinania
Zgodnie z [14], kl. 7.1 (2) warunek interakcji zginania i ścinania należy sprawdzać w przekrojach, znajdujących się w odległości nie mniejszej niż $\frac{h_w}{2}$ od podpory z żebrami pionowymi. Spośród tych przekroi należy wyselekcjonować te, w których działa duża obliczeniowa siła poprzeczna $V_{Ed}$ przekraczająca 50% nośności plastycznej środnika przy ścinaniu $V_{bw}$ (krzywa A-C na rys. 19). Tylko w tych przekrojach wymagane jest sprawdzenie interakcji zginania i ścinania, które dokonuje się z warunku [14]), (przekształcone (7.1):
$$\begin{equation} M_{Ed} \le M_{f,Rd}+ (M_{pl,Rd} – M_{f,Rd} ) \left [ 1-\left ( \cfrac{2V_{Ed}}{V_{bw,Rd}}-1 \right )^2 \right ] \label{39} \end{equation}$$
gdzie: $V_{bw,Rd}$,
$ M_{f,Rd}$ – obliczeniowa nośność przekroju złożonego wyłącznie z pasów (przekrój sandwich). Określa ona górną granicę zakresu w punkcie B na rys. 19. W przypadku, gdy pas nie jest stężony, to należy uwzględnić stosowny współczynnik niestateczności, a w przypadku, gdy pas może utracić stateczność miejscową (np efekt szerokiego pasa), to należy uwzględnić szerokość efektywną ( z pominięciem obszarów wyboczonych) w klasyczny sposób.
$ M_{pl,Rd}=M_{f,Rd}+M_{pl,w,Rd}=b_f \cdot t_f \cdot (h_w+t_f)\cdot f_{yf}+\cfrac{t_w h_w^2}{4}\cdot f_{yw}$ – nośność plastyczna całego przekroju liczona z pominięciem efektu klasy ścianek (jak dla klasy 1).
W obszarze małych momentów zginających ( krzywa A-B na rys. 19), definiowanego dla wartości momentu zginającego $ M_{Ed} \le M_{f,Rd}$ siła poprzeczna $ V_{Ed}$ jest ograniczona do wartości „tylko środnik”, tj do $V_bw,Rd$.
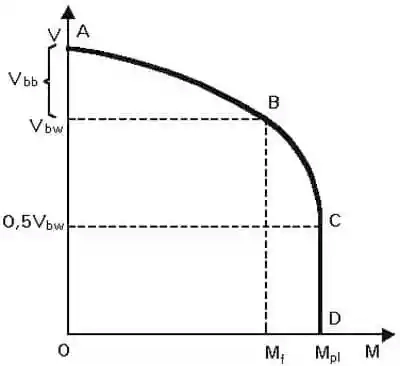
Rys. 19 Interakcja nośności na ścinanie i zginanie [10] (Interakcja w metodzie kratownicowej (pola ciągnień) Inte
Interakcja zginania i siły podłużnej
W przypadku występowania siły podłużnej $N_{Ed}$ należy redukować nośność pasów $M_{f,Rd}$ oraz przekroju $M_{pl.Rd}$ stosownie do postanowień [14], kl. 5.4 (2) i [15], kl.6.2.9 .
Interakcja obciążenia skupionego, zginania i siły podłużnej
Jeśli oprócz momentu zginającego $M_{Ed}$ i siły podłużnej $N_{Ed}$ do pasa ściskanego dźwigara przyłożone jest obciążenie skupione $F_{Ed}$, to nośność sprawdza się jak wyżej, a ponadto powinien być spełniony warunek [14], przekształcony (wzór 8.1 )
$$\begin{equation} \cfrac{F_{Ed}}{\cfrac {f_{yw}L_{eff} t_w}{\gamma_{M1}}+0,8 \cfrac{M_{Ed}}{M{pl,Rd}} } \le 1,4 \label{40} \end{equation}$$
Stateczność blachownicy
Typy niestateczności blachownicy
W tab.1 zestawiono typy niestateczności (wyboczenia) blachownicy. Dotychczas omówiliśmy zagadnienie niestateczności środnika (poz 1 w tab.1 )
Tab.1. Typy niestateczności (wyboczenia) blachownicy [10]
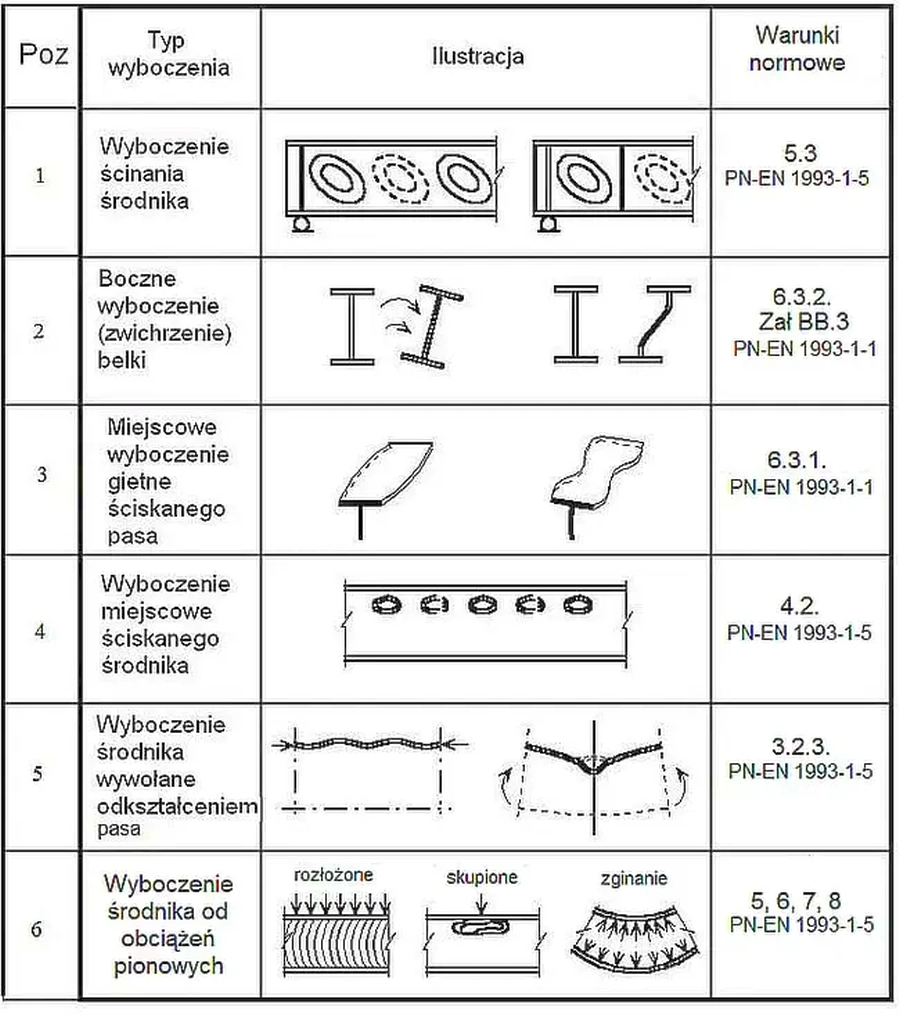
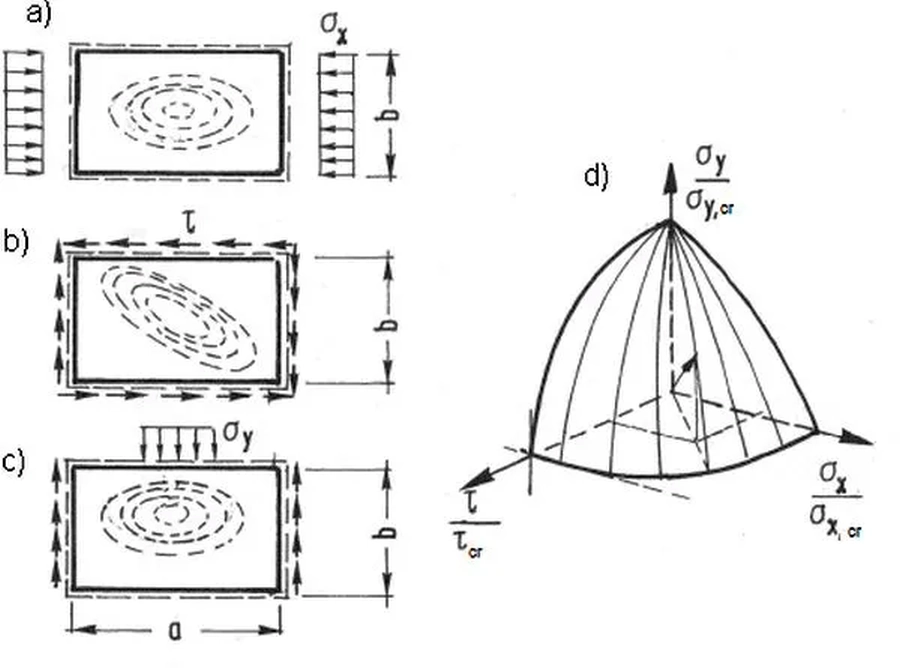
Rys. 20 Typy niestateczności środnika: a) od ściskania, b) od ścinania, c) od docisku, d) interakcja [13]-str. 408
Poszczególne typy niestateczności panelu środnika charakteryzuje specyficzna forma wyboczenia płyty (rys. 20): a) wyboczenie pod wpływem ściskania powodują poziome wybrzuszenia na w poziomej osi obciążenie, b) wyboczenie pod wpływem ścinania powodują ukośne wybrzuszenia, c) wyboczenie pod wpływem ściskania powoduje pojawienie się poziomych wybrzuszeń pod obciążeniem. Działanie jednoczesne ściskania$\sigma_x$, ścinania $ \tau$ oraz docisku $\sigma_y$ podlega interakcji, pokazanej na rys. 20 d).
Nośność nadkrytyczna i metoda przekroju efektywnego
Płaska ścianka płytowa wykazuje nośność znacznie przewyższającą klasyczną nośnością krytyczną, wynikającą z teorii wyboczenia sprężystego (teorii bifurkacyjnej lub Eulera). Zjawisko to nazywane jest nośnością nadkrytyczną. Inżynierska teoria nośności nadkrytycznej w uproszczeniu zakłada, że z całego przekroju płyty wyłącza się części środkowe(rys. 21a), a do pozostałych części, przylegających do krawędzi usztywnień przykłada się w sposób równomierny naprężenie pozostające w równowadze z całkowitym obciążeniem. Prowadzi to do zadania wyznaczenia przekroju efektywnego, złożonego z części płyty o szerokościach $b_{eff}$ (rys.16b).
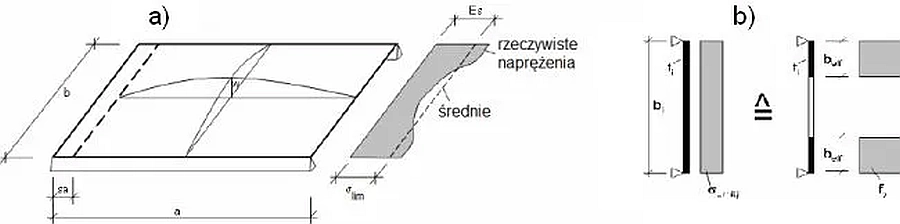
Rys. 21. Nośność nadkrytyczna płyty: a) model rzeczywisty, b) model efektywny (ścianki współpracujące)
Niestateczność typu płytowego
Redukcja przekroju złożonego z płyt ściskanych do przekroju efektywnego, powinna być prowadzona iteracyjnie, wychodząc z rozkładu naprężeń dla przekroju oryginalnego (niezredukowanego). W normie [14] podano przybliżone formuły do wyznaczenia szerokości efektywnych (współpracujących ścianek płyt wspornikowych (Typ W) zestawiono w tab.2, a ścianek płyt przęsłowych (Typ P – panele podparte na dwóch krawędziach) w tab.3.
Tab.2. Szerokość efektywna ścianek wspornikowych płyt (Typ W) [14]
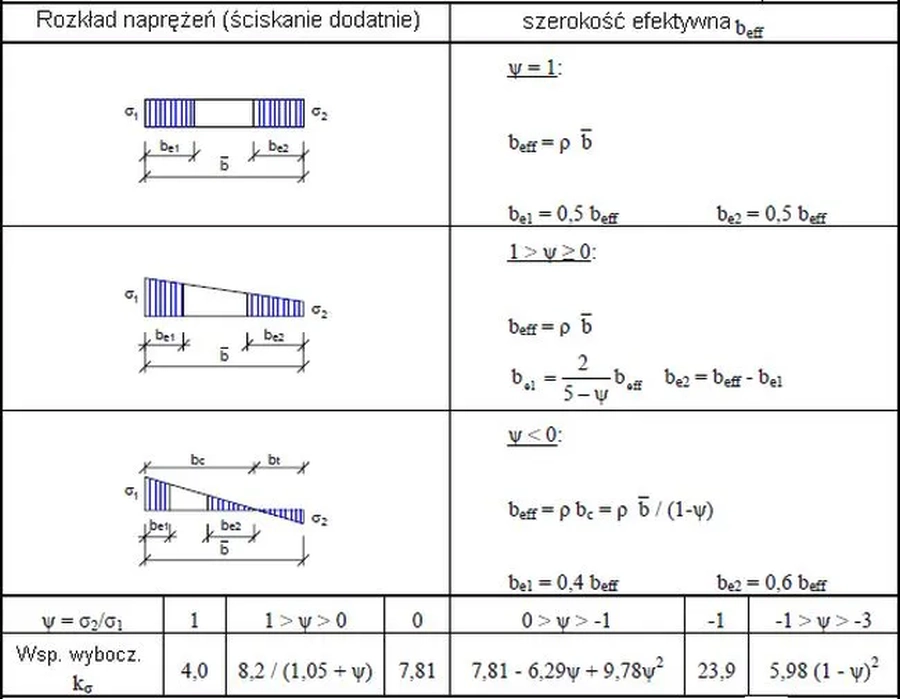
Tab.3. Szerokość efektywna ścianek przęsłowych płyt (Typ P) [14]
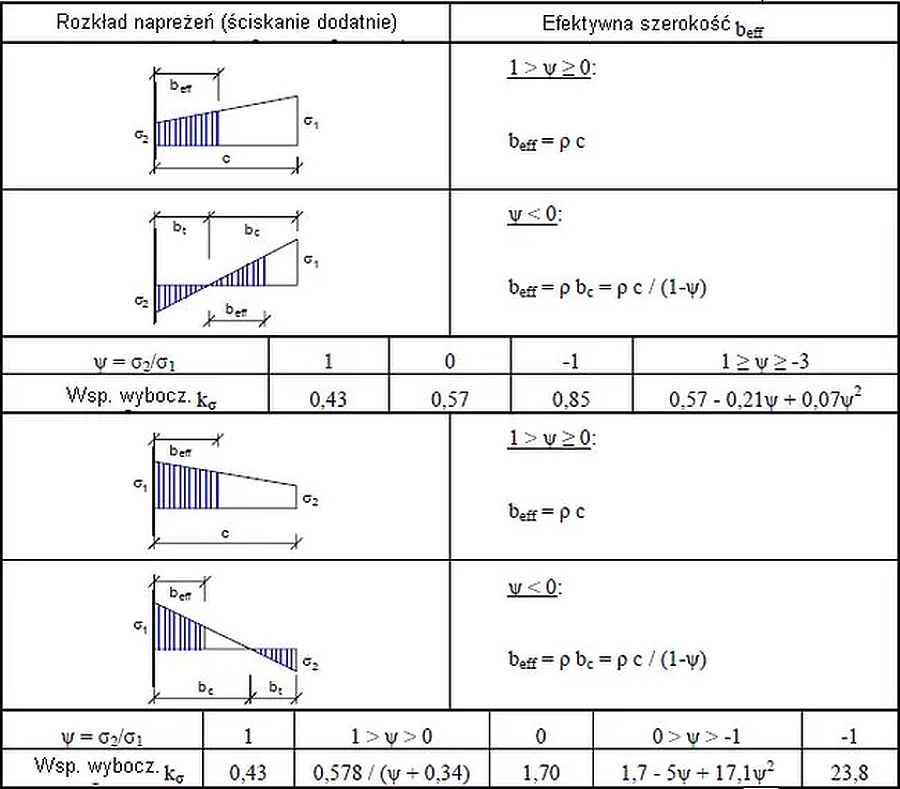
Szerokość efektywną (współpracującą) ścianki $b_{eff}$ zgodnie z [14] wyznaczamy z prostej formuły:
$$\begin{equation} b_{eff}=\rho \overline b \label{41} \end{equation}$$
gdzie szerokość miarodajna ścianki $\overline b$ jest równa wysokości środnika w świetle spoin $ h_w-2\cdot a_s$, lub szerokości wspornikowej części pasa $c=\frac{1}{2}(b_f-t_w)-a_s$ ($a_s$ – grubość spoiny pasowej.
Wyznaczenie współczynnika redukcyjnego niestateczności ścianki $\rho$ jest dosć żmudne i dokonuje się w zależnosci od względnej smukłości płytowej ścianki $\lambda_p$, która zgodnie z zasadą dla naprężenia krytycznego płytowego $\sigma_{cr,p}$, wynosi :
$$\begin{equation} \overline \lambda_p=\sqrt{\cfrac{N_R}{N_{cr}}}\sqrt{\cfrac{A_c f_y}{A_c \sigma_{cr,p}}}=\sqrt{\cfrac{f_y}{\rho\sigma_{cr} }} \label{42} \end{equation}$$
Po uwzględnieniu tego, że sprężyste naprężenia krytyczne płytowe $\sigma_{cr,p}$ wynoszą
$\sigma_{cr,p}=k_\sigma \cdot \sigma_E= k_\sigma \cfrac{\pi^2 E}{12 (1-\nu^2)} (\frac{t}{\overline b})^2$
gdzie $k_\sigma$ jest współczynnikiem wyboczenia, obliczanym na podstawie tab 2 i 3.
i dla $E= 210 GPa$, $\nu=0,3$ i współczynnika materiałowego $\varepsilon= \sqrt{ \frac{235}{f_y}}$ otrzymujemy:
dla $\overline \lambda_p \le \overline \lambda_{p,lim}$ współczynnik redukcyjny $\rho=1,0 $
$$\begin{equation} \overline \lambda_p=\cfrac{\cfrac{\overline b}{t}}{28,4 \varepsilon \sqrt{k_\sigma}} \label{43} \end{equation}$$
a dla większych smukłości ścianki :
$$\begin{equation}\rho= \cfrac{\overline \lambda_p- A_p} {\overline \lambda_p^2}\label{44} \end{equation}$$
gdzie $\overline \lambda_{p.lim}$ oraz $A_p$ zależy od typu panelu (Typ W lub P wg tab 2 i 3):
dla typu P $A_p=0,055(3+\psi) \ge 0$, $\overline \lambda_{p.lim}=0,673 $
dla typu W $A_p = 0,188 $ , $\overline \lambda_{p.lim}=0,748 $
Stosunek naprężeń krawędziowych $\psi$ zdefiniowano w tab.2 i 3 wyznacza się na podstawie cech przekroju brutto, ewentualnie z uwzględnieniem efektu szerokiego pasa. Wyznaczając ten stosunek w środniku przyjmuje się pole przekroju środnika brutto i efektywne pole przekroju pasa ściskanego.
Niestateczność typu prętowego
W panelach krótkich o stosunkach boków $\frac{a}{b}<1$ (rys. 22b),lub paneli bez podparcia podłużnego (rys.22a), lub paneli użebrowanych o dużym stosunku boków może wystąpić niestateczność płyty typu prętowego w pokazanych modelach.
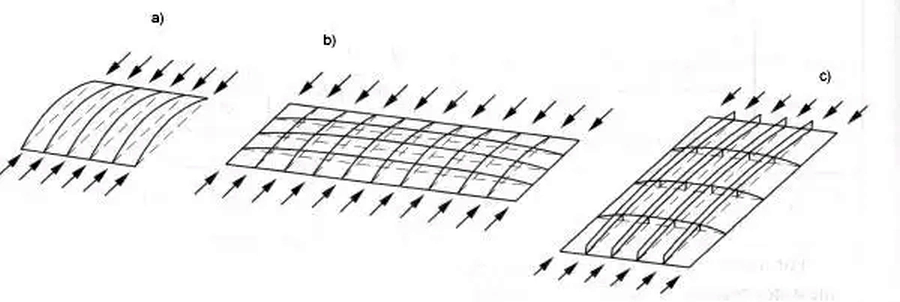
Rys.22. Modele niestateczności typu prętowego: a) niestateczność panelu bez podparcia podłużnego, b) niestateczność panelu nieużebrowanego o małym stosunku boków, c) niestateczność panelu użebrowanego o dużym stosunku boków
W modelu zachowania płyty w sytuacji niestateczności prętowej polega na usunięciu podłużnych podpór elementu. W zależności o typu użebrowania środnika naprężenia krytyczne przy niestateczności typu prętowego $\sigma_{cr,c}$ oraz względną smukłość płytową $\overline\lambda_c$ wyznacza się ze wzorów:
- w ściankach nieużebrowanych:
$\sigma_{cr,c}= \cfrac{\pi^2E t^2}{12(1-\nu^2)a^2}$,
$\overline\lambda_c=\sqrt{\cfrac{f_y}{\sigma_{cr,c}}}$ - w ściankach użebrowanych na podstawie zachowania najbardziej ściskanego żebra skrajnego:
$\sigma_{cr,c}= \cfrac{\pi^2E I_{sl,1}}{A_{sl,1}a^2}$,
$\overline\lambda_c=\sqrt{\cfrac{\beta_{A,C} f_y}{\sigma_{cr,c}}}$
gdzie: $A_{sl,1$}$, $I_{sl,1}$ – pole przekroju i moment bezwładności przekroju pręta zastępczego brutto, złożonego z żebra i przyległych części ścianki, moment bezwładności względem osi równoległej do płaszczyzny panelu.
Współczynnik redukcyjny nośność przy niestateczności typu prętowego jest współczynnikiem wyboczeniowym wyznaczanym w sposób standardowy dla smukłości względnej (31b), czyli z zależności:
$$\begin{equation}\chi_c=\cfrac{1}{\Phi \sqrt{\Phi^2- \overline\lambda_c^2}}\\
\Phi=0,5 [1+\alpha_e ( \overline\lambda_c-0,2)+ \overline\lambda_c^2]\\
\alpha_e=\alpha+\cfrac{0,9}{\frac{i}{e}}\\
i=\sqrt{\frac{I_{sl,1}}{A_{sl,1}}}\\
e=max \{e_1, e_2 \}\\
\label{45} \end{equation}$$
Interakcja niestateczności typu płytowego i typu prętowego
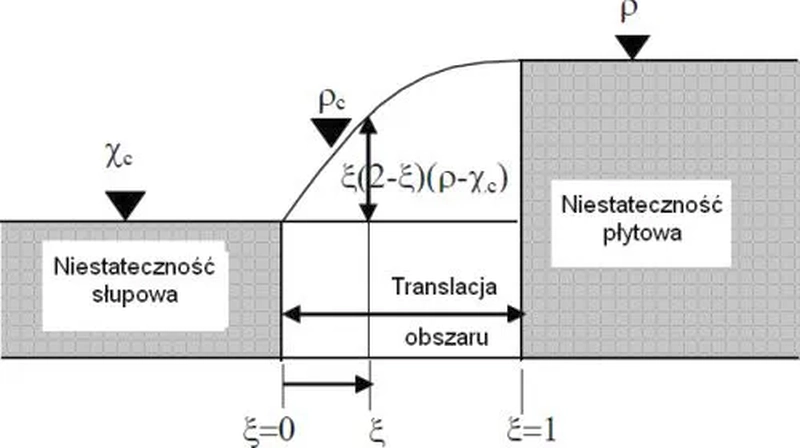
Rzeczywista niestateczność panelu płyty najczęściej jest typu mieszanego typu płytowo-prętowego, czyli znajduje się pomiędzy dwoma ekstremalnymi sytuacjami: niestatecznością typu płytowego i typu słupowego, opisanymi wyżej. Rzeczywisty współczynnik redukcyjnych $\rho_c$ znajduje się pomiędzy współczynnikami obu tych typów: $\rho$ oraz słupowego $\chi_c$ : $\chi_c \le \rho_c < \rho$ i może być interpolowane zgodnie rys.23 z zależności:
$$\begin{equation}\rho_c=\xi(2-\zeta)(\rho-\chi_c)+\chi_c \\
\xi=\cfrac{\sigma_{cr,p}}{\sigma_{cr,c}}$ , lecz $ 0\le \xi\le 1\\
\label{46} \end{equation}$$
Zwichrzenie blachownicy
Wyboczenie boczne nazywane w polskiej literaturze zwichrzeniem zostało zobrazowane w wierszu 2 tab 1. Zwichrzenie jet przedmiotem pkt 6.3.2 normy [11] i podstawową wielkoscią umożliwiająca klasyczną analizę jest moment krytyczny $M_{cr}$, który wraz z pwoszechnym dostępem do szybkich programów na licencji free należy wyznaczać numerycznie. Tradycyjne analizy i wzory straciły na znaczeniu. Do analizy wyboczenia bocznego belek stosuje się program LTBEAM (licencja free), a do znalizy ram program Consteel (komercyjnyc).
Żebrowanie środnika
W przypadku, gdy nośność środnika jest zbyt mała wykonuje się żebrowanie środnika.
Środnik blachownic można żebrować poprzecznie żebrami pionowymi 1, 3 lub podłużnie żebrami poziomymi 2 (rys.24). Najczęściej stosuje się żebra poprzeczne, standardowo pod każda siła skupioną, w tym nad podporami. żebra podłużne są stosowane w ściskanej strefie środnika w przypadku potrzeby podwyższenia nośności środnika – powodują one jednak wzrost pracochłonności wykonania środnika, dlatego w takich przypadkach najczęściej zwiększa się nieco (np o 1 mm) grubość środnika bez żebrowania podłużnego.
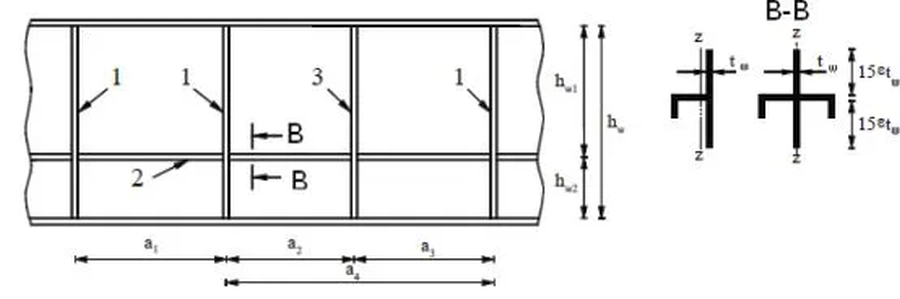
Rys. 24 Typy żeber środnika blachownicy: 1,3 -poprzeczne, 2- podłużne (zmodyfikowany rys. 5.3. [14]
Do pasa ściskanego żebro usztywniające mocuje się bezpośrednio spoinami pachwinowymi. Połączenie z pasem rozciąganym należy konstruować w sposób pokazany na rys. 25 26 .
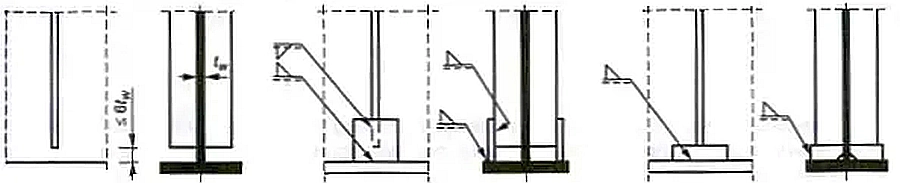
Rys.25 Połączenie żeber w strefie rozciągania [16], str. 365
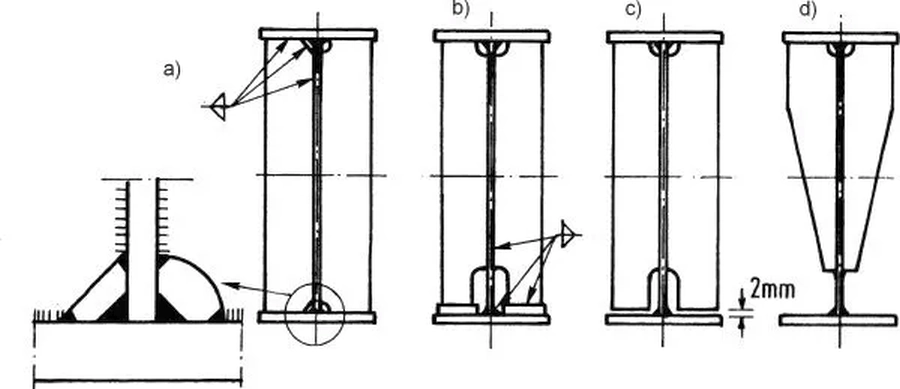
Rys.26 Kształtowanie żeber przy pasie rozciąganym: ścięcia proste ok 3 $a_s$, b) ścięcie podłużne z podkładką, c) ścięcie podłużne ze szparą 2 mm, d) krótkie zebra [13]-str. 722
Rozróżnia się żebra podporowe (nad podporą) lub pośrednie (pomiędzy podporami). Ważnym pojęciem są żebra sztywne oraz żebra podatne. Nie podano jednoznacznie granicy dla której żebro podatne staje się sztywnym. Można jednak wnosić, że kryterium takim jest kryterium konstrukcyjne (wymiarów żebra).
Wymagania dotyczące sztywności żeber poprzecznych podano w [14], kl. 9.2.1 , a dotyczące żeber podłużnych w [14], , kl. 9.2.2. Poniżej zamieszczono tylko wybrane najczęściej stosowane warunki.
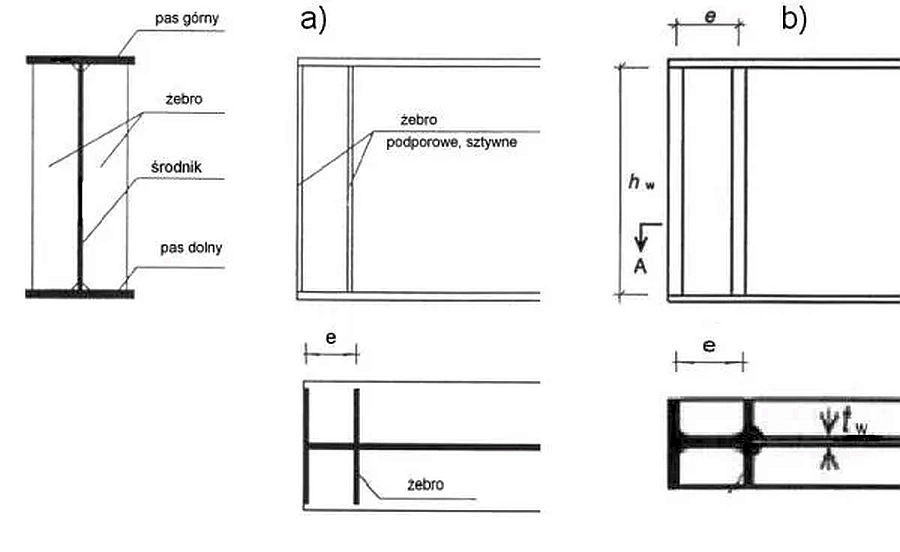
Żebra skrajne i podporowe sztywne lub podatne
Żebra skrajne (najczęściej podporowe) traktujemy jako sztywne, jeśli jest podwójne, to znaczy złożone z dwóch dwustronnych żeber poprzecznych , stanowiących pasy belki krótkiej o długości $h_w$ (rys. 27a). Funkcję sztywnego żebra skrajnego często spełnia dwuteownik walcowany, przyspawany do środnika dźwigara w sposób pokazany na rys. 27b.
Na rys. 28 pokazano typowe podporowe żebro nad podporą pośrednią blachownicy.
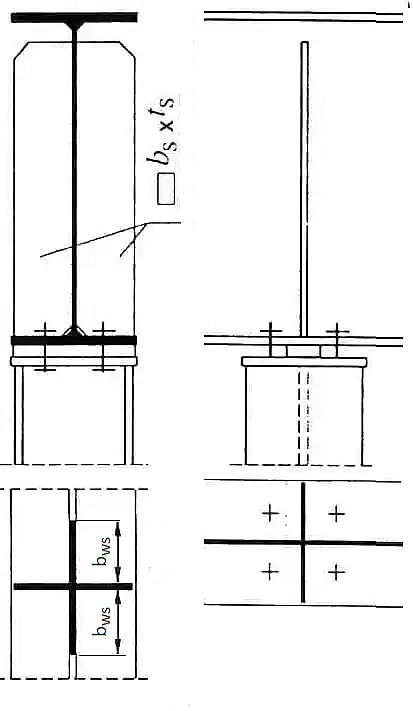
Rys. 28 Żebro nad podporą pośrednią [17]
Każde dwustronne żebro podporowe z płaskowników powinno mieć pole przekroju $A_{st}$, spełniające warunek
$$\begin{equation} A_{st} > \cfrac{4\cdot h_w \cdot t_w^2}{a} \label{47} \end{equation}$$
gdzie:
$ a > 0,1 \cdot h_w$ – podłużny rozstaw osiowy żeber,
$h_w$ – wysokość środnika.
Żebro podporowe podatne, to takie, które nie spełnia warunków ($/ref{47}$) lub ($/ref{48}$) i jest najczęściej wykonane z pojedynczych płaskowników dwustronnych w osi podpory.
Dobrym rozwiązanie jest zaprojektowanie żebra skrajnego podporowego z rury okrągłej, co powoduje zwiększenie sztywności skrętnej na skręcanie skrepowane i bimoment.
Żebra pośrednie sztywne lub podatne
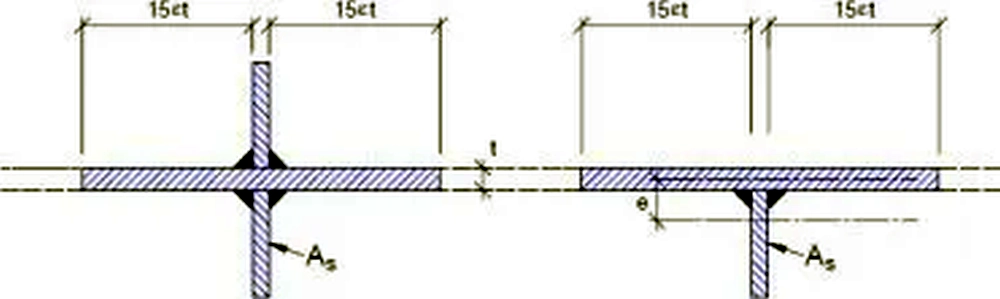
Rys. 29 Efektywne pole przekroju żebra rys.9.1. [14]
Żebro pośrednie sztywne jest wykonane z pojedynczych, dwustronnych płaskowników i powinno spełniać szereg warunków sztywności przekroju efektywnego, to znaczy dla przekroju wraz z częścią współpracującego środnika po $15\varepsilon t$ $(t=t_w$ z każdej strony żebra (rys.29).
Żebra pośrednie sztywne są najczęściej wykonane z pojedynczych obustronnie umieszczonych płaskowników, które powinny spełniać warunki momentu bezwładności żebra efektywnego $I_{st} =
Oznacza to, że dla przekroju należy przyjmować pole przekroju brutto żebra powiększone o efektywne odcinki środnika (z każdej strony żebra) wynoszące po 15εt. Żebro uważa się za sztywne, jeśli moment bezwładności Ist spełnia poniższe warunki:
$$\begin{equation} I_{str} \ge = \begin {cases}
1,5 \cdot \cfrac{(h_w \cdot t_w)^3}{a^2} & \textrm { jeśłi } \cfrac{a}{h_w} < \sqrt{2}\\
0,75 \cdot h_w \cdot t_w^3 & \textrm { jeśłi } \cfrac{a}{h_w} \ge \sqrt{2}\\ \\
\end {cases} \label{49}\end{equation}$$
Żebra podłużne
Żebrowanie podłużne blachownicy (np żebro 2 na rys. 24) może być wykonane w sposób pokazany na rys. 8.
Sprawdzanie nośności żeber podporowych
Żebra podporowe podatne
Wytrzymałość i stateczność żebra przy wyboczeniu giętnym z płaszczyzny środnika sprawdza się w sposób klasyczny dla przekroju efektywnego (ze 2współpracującą częścią środnika)
Sprawdzeniu podlega też wyboczenie skrętne żebra w sytuacji, gdy pracuje tylko jeden płaskownik żebra ( z jednej strony środnika)
Nośnośc żebra na docisk wyznacza się dla powierzchni żebra $A_b=2t_s\cdot (b_s-a_s)$ z uwzględnieniem (pominięciem) ich ścięcia $a_s$ w styku pasa ze środnikiem. Przyjmuje się, że żebra przenoszą część obciążeń poprzecznych wynikającą z ich nośności przez docisk. Pozostała część przenoszona jest przez środnik.
Sprawdzanie nośności żebra pośredniego
Żebro poprzeczne pośrednie wymiaruje się jako ściskany i zginany pręt z wstępną imperfekcją geometryczną zgodnie z ogólnymi zasadami przedstawionymi na rys.30. Różnica w stosunku do sprawdzania nośności żeber skrajnych zawiera się głównie w tym, że żeber skrajnych nie obciąża się siłami imperfekcji.
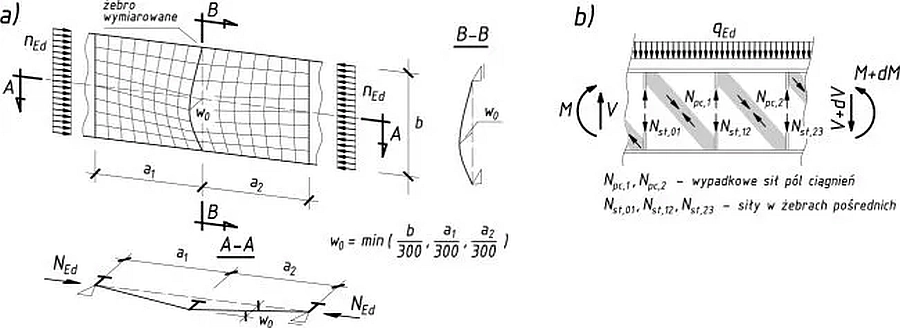
Rys.30 Model obliczeniowy żebra pośredniego blachownicy a) schemat statyczny, b) obciążenie od pola ciągnień
Zalecaną metodą ogólną jest metoda imperfekcyjna [1], to znaczy wyznaczenie sił w procedurze II rzędu po obciążeniu pręta obciążeniami równoważnymi od imperfekcji i sprawdzenie naprężeń wywołanych siłami drugiego rzędu bez wyznaczania współczynników wyboczeniowych ( w tym skrętnych i bocznych – zwichrzenia). Sprawdzenia maksymalnych naprężeń normalnych w przekroju żebra $\sigma_{z, max}$ i ugięć dokonuje się z zależności ($\ref{50}$)
$$\begin{equation} \sigma_{z,max} \le \cfrac{f_y}{\gamma_{M1}}\\ u_{y.max} \le u_{dop}=\cfrac{b}{300}
\label{50}\end{equation}$$
W przedkrytycznej fazie pracy blachownicy naprężenie $\sigma_z$ są efektem działania obciążenia rozłożonego od imperfekcji, działającego poprzecznie na słupek kratownicy zastępczej (żebro):
$$\begin{equation} q_{eq}=\cfrac{\pi}{4} (w_0+w_{el}) \cfrac{\sigma_{cr,c}}{\sigma_{cr,p}} \left[ \left( \cfrac{1}{a_1}+\cfrac{1}{a_2}\right) \cfrac{N_{Ed}}{b}\right]
\label{51}\end{equation}$$
gdzie:
$w_0$ – strzałka wygięcia wstępnego (imperfekcja) pręta; $w_{el}$ – strzałka ugięcia żebra, która zwykle przyjmuje się jako maksymalną dopuszczalną $w_{el}=\frac{b}{300}$,
$\sigma_{cr,c}$ – sprężyste naprężenie krytyczne ścianki nieużebrowanej przy niestateczności typu prętowego,
$\sigma_{cr,p}$ – sprężyste naprężenie krytyczne ścianki nieużebrowanej przy niestateczności typu płytowego.
Po przejściu blachownicy do stanu nadkrytycznego w żebrze, stanowiącym słupek kratownicy zastępczej uaktywnia się siła podłużna $N_{st}$ (rys.30b).
Żebra w załamaniach pasów
W załamaniach pasów należy umieszczać żebra i dobierać je na siły, stanowiące wypadkową nośności zbiegających się pasów w sposób pokazany na rys. 31.
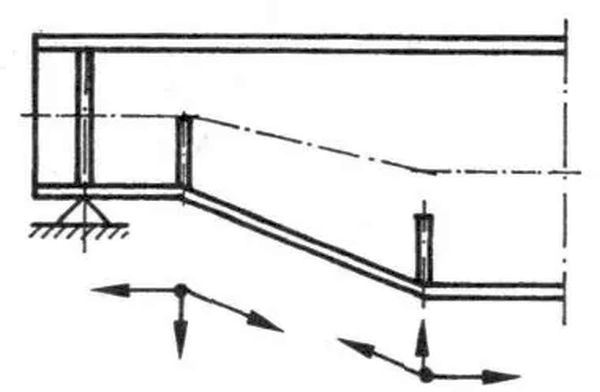
Rys.31 Kształtowanie i obliczanie żeber w załamaniach pasów [13], str. 724
Sprawdzenie przemieszczeń blachownicy
Sprawdzenie stanu granicznego użytkowania w belkach stropowych polega na sprawdzeniu, czy jest zachowany warunek
$$\begin{equation} \delta \le \delta_{dop} \label{52}\end{equation}$$
gdzie:
$\delta$ strzałka ugięcia belki wywołana obciążeniami charakterystycznymi ,
$\delta_{dop}$ akceptowana strzałka ugięcia.
Oryginalna norma EN 1993-1-1 nie określa granicznych wartości ugięć i przemieszczeń elementów. Zamiast tego zawarto zalecenie, że kryteria stanu granicznego użytkowalności, w tym graniczne wartości ugięć i przemieszczeń powinny zostać uzgodnione z inwestorem. Ponadto kryteria dotyczące granicznych wartości ugięć i przemieszczeń7powinny być tak dobrane, żeby zapewniały komfort użytkowania obiektu, funkcjonalność itp. Co prawda w załączniku krajowym do normy [11] zdefiniowano graniczne ugięcia normowe, ale są to tylko zalecenia, a nie bezwzględne wymogi:
$$\begin{equation} \delta_{dop} = \begin {cases}
\cfrac{L}{250} & \textrm { dla belek zwykłych} \\
\cfrac{L}{300} & \textrm { dla belek stropowych wrażliwych na ugięcia (np stropy otynkowane lub z płytami g-k)} \\
\end {cases} \label{53}\end{equation}$$
Często graniczne ugięcia powinny być jeszcze mniejsze. Na przykład zgodnie ze „starą” normą PN/B-03200 obowiązywały ograniczenia:
dla stropów i pomostów obciążonych maszynami $\delta_{dop}= \frac {L}{450}$,
dla stropów obciążonych kolejkami $\delta_{dop}= \frac {L}{350}$,
dla podciągów, belek stropowych i pomostowych od obciążenia użytkowego w stropach otynkowanych $\delta_{dop}= \frac {L}{360}$
W każdym przypadku ugięcia graniczne określa Projektant na podstawie wymogów użytkowych ustalanych indywidualnie dla konkretnej sytuacji projektowej.
Połączenie belek poprzecznych z blachownicą
Na rys. 32 pokazano typowe , przegubowe połączenia belek stropowych z blachownicą. W połączeniu rys. 32c) i d) z żebrem blachownicy zastosowano podcięcia pasów i środnika blachownicy. Na rys. 32 f1) pokazano, że brak wyokraglenia skutkuje karbem, w którym wsytąpi pęknięcie. Można temu zaradzić poprzez wyokrąglenie podcięcia w sposób pokazany na rys. 32 f), lecz częściej stosuje s wiercenie otworów (rys. f3), które prowadzą do wyokrągleń pokazanych na rys. 32.
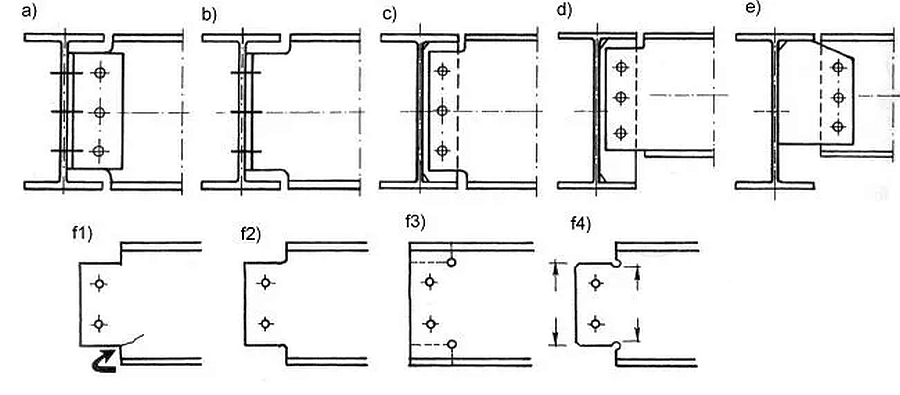
Rys. 32 Połączenie śrubowe belek stropowych z blachownicą: a)a kątownikami, b) czołowe, c), d) zakładkowe z żebrem, e) poprzez blachę boczną, f1-4) potrzeba wyokrągleń podcięć[13]-str. 743
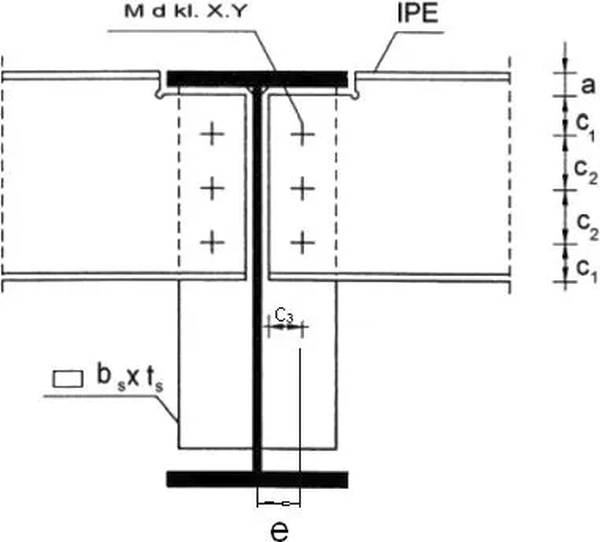
Połączenie belek stropowych z żebrami blachownicy często wykonuje się jako śrubowe zakładkowe rys. 32d). Poniżej pokazano sposób sprawdzania wytężenia takiego połączenia (rys.33).
Siła poprzeczna jest przenoszona przez środnik blachownicy w płaszczyźnie jej osi symetrii na mimośrodzie $e$ w stosunku do linii osi śrub M d kl. X.Y.
W osi grupy śrub ( w tym przypadku w śrubie środkowej) działają więc siły:
$$\begin{equation} \text { siła poprzeczna } \quad V_{Ed}\\
\text { moment } \quad M_{Ed}=V_{Ed}\cdot e \label{54}\end{equation}$$
W śrubach działają następujące siły:
$$\begin{equation} \text { od siły poprzecznej } \quad F_{V,i,Ed}=\cfrac{V_{Ed}}{n}\\
\text { od momentu } \quad F_{M,i,Ed}= \cfrac{M_{Ed}r_i}{\Sigma r_i^2}\\
\text { wypadkowa } \quad F_{i,Ed}=\sqrt{F_{V,i,Ed}^2+F_{M,i,Ed}^2}
\label{55}\end{equation}$$
gdzie:
n- liczba s rub (na rys 33. n=3),
$r_i$ – promień – odległość i-tej śruby od środka grupy śrub.
Przy oznaczeniu śrub od góry:1,2,3, mamy: $r_1=c_2$, $r_2=0$, $r_3=c_2$.
Maksymalna siła działa w śrubie 1 lub 3 o wartości $F_{Ed}=V_{Ed} \sqrt{(\frac{1}{3})^2+ \cfrac {e \cdot c_2}{2\cdot c_2^2}}$
Nośność śruby wyznacza sie zgodnie z zasadami jako minimum z nośności na ścinanie $F_{v,Rd}$ i docisk $F_{b,Rd}$, przy czym należy zwrócić uwagę na to, że nośność śrub na docisk jest inna w kierunku poprzecznym do osi belki oraz w kierunku osi belki ze względu na inne odległości otworów od krawędzi.
Warunek nośności śruby można zapisać w postaci
$$\begin{equation} F_{i,Rd}= min[F_{v,i,Rd},F_{b,i, Rd}] > F_{i, Ed} \label{56}\end{equation}$$
Ponadto powinien być spełniony warunek nośności na rozerwanie blokowe:
$$\begin{equation} V_{eff,2,Rd}> V_{Ed} \label{57}\end{equation}$$
gdzie obliczeniowa nośność na rozerwanie blokowe wynosi
$$\begin{equation} V_{eff,2,Rd}= \cfrac{0,5 \cdot f_u A_{nt}}{\gamma_{M2}} + \cfrac {f_y \cdot A_{nv}}{\sqrt{3}\cdot \gamma_{M0}} \label{58}\end{equation}$$
Powyżej wprowadzono oznaczenia:
$A_{nt}=t_p(c_3-\frac{d_0}{2})$ – przekrój netto na rozciąganie ($t_p$ – grubość środnika belki, $c_3$ – wg rys.33,
$d_o=d+2$ – średnica otworu pod śrubę o średnicy $d$),
$A_{nv}= t_p(c_1+c+2+c_2-d_0-d_0-\frac{d_0}{2})$ – przekrój netto na rozciąganie ($c_1, \,c_2$) – wg rys.33,
$\gamma_{M2}=1,25$ – współczynnik bezpieczeństwa (materiałowy) dla śrub.
W przypadku zaprojektowania belek stropowych ciągłych ich połączenia z blachownicą oraz uciąglenie można wykonać w sposób pokazany na rys. 34.
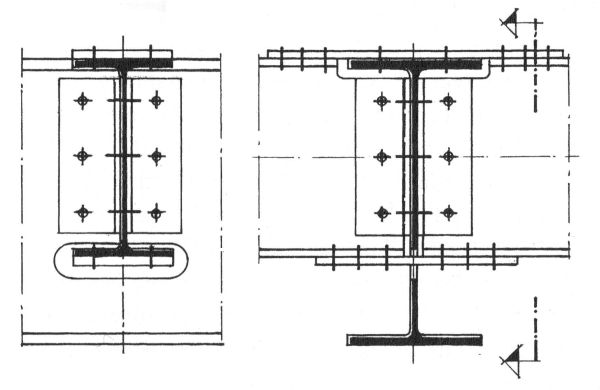 Rys. 34 Uciąglenie belek stropowych na przejściu przez blachownicę [13], str. 740
Rys. 34 Uciąglenie belek stropowych na przejściu przez blachownicę [13], str. 740
Połączenia warsztatowe środnika i pasów
Połączenia warsztatowe wykonywane są jako spawane i służ a przede wszystkim do zmian przekrojów pasów lub połączeń technologicznych odcinków blach. Na rys. 35 przedstawiono zalecane sposoby łączenia spoinami: a) pasów o takiej samej grubości, o różnicy grubości $<10 mm$, i o większej różnicy grubości z wyrównaniem dolnej płaszczyzny, b) symetryczne połączenie środnika o różnej grubości. Sposoby przygotowania do spawania krawędzi pakietów pasów są przedstawione na rys.8. Czasami potrzebne jest połączenie blach środnika i pasów jednocześnie. Wówczas można stosować rozwiązania pokazane na rys. 36. Nad stykiem rozciąganego pasa należy wykonać w styku środnika, wypadającego w miejscu styku pasów.
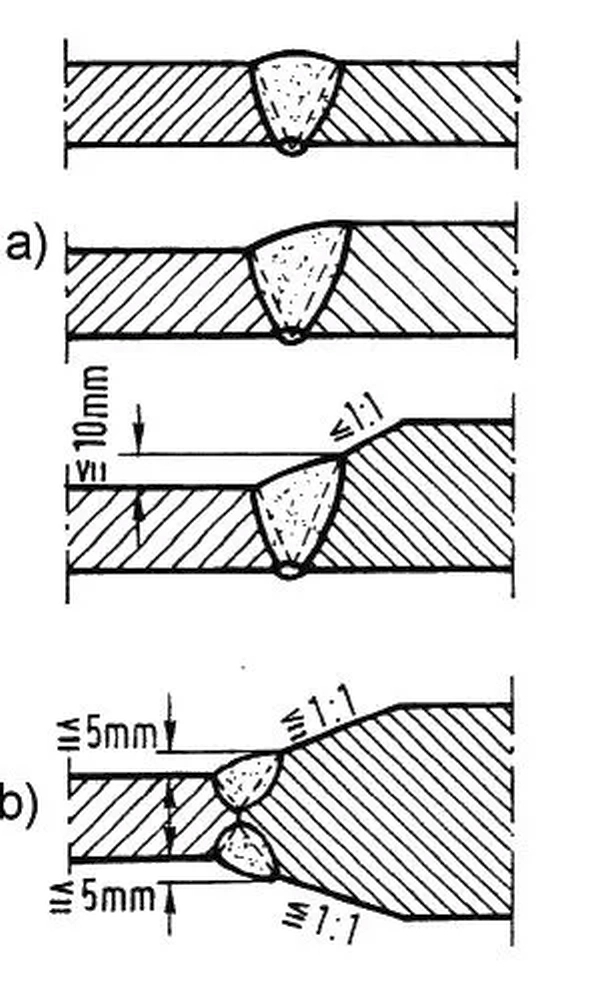
Rys.35 Szwy spawane pasów i środnika blachownic: a) pasów, b) środnika [13]-str. 729
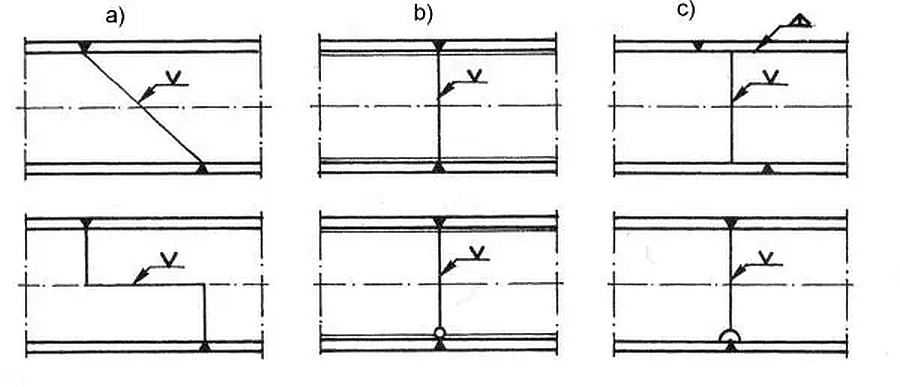
Rys.36 Spawane styki blachownicy: a) ukośny lub łamy styk środnika, przesunięte styki pasów, b) styk w jedenj linii, c) poprzeczny styk środnika[13]-str. 727
Połączenia montażowe belek i ram blachownicowych
Połączenia montażowe elementów blachownicy najczęściej wykonuje się jako doczołowe sprężane śrubami wysokiej wytrzymałości. Połączenia doczołowe na śruby zwykłe i sprężane omówiono w rozdz. 4 artykułu Połączenia śrubowe.
Na rys. 37 pokazano przykłady połączeń montażowych rygla ze słupem zastosowaniem śrub zwykłych, to znaczy połączeń, które nie są sprężane. Śruby w nich najczęściej są wstępnie sprężone na 50% pełnego momentu sprężającego, co ma zabezpieczyć śruby przed odkręceniem.
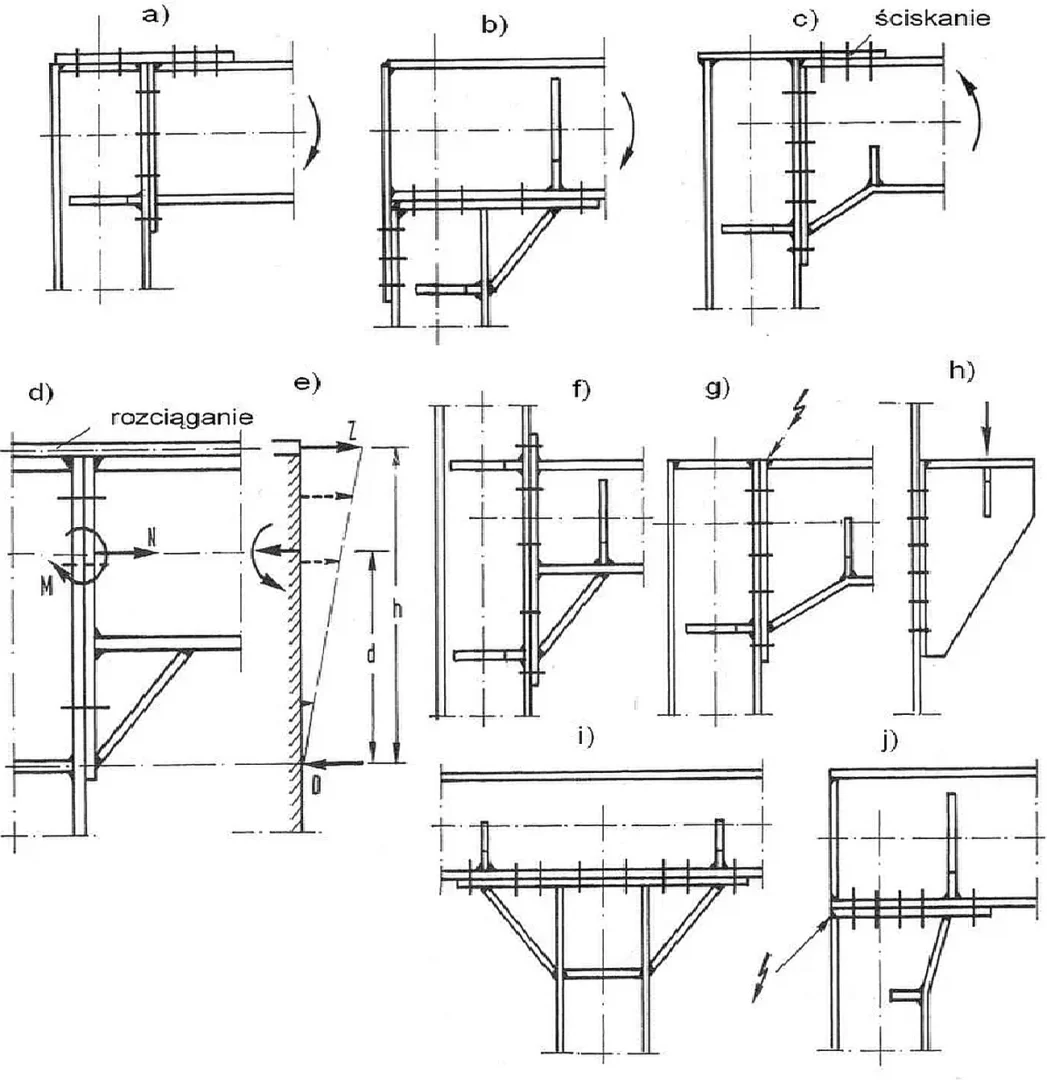
Rys.37 Przykłady połączeń montażowych rygla ze słupem [13], str. 756
Przykładowo nacisk żebra $D$ dla przypadku z rys. 37e (dolny) można wyznaczyć z zależności:
$$\begin{equation} V_{eff,2,Rd}= \cfrac{0,5\cdot f_u A_{nt}}{\gamma_{M2}}+\cfrac {f_y \cdot A_{nv}}{\sqrt{3} \gamma_{M0}}\\
M+ N d= Z \cdot h \to Z = \cfrac {M+Nd}{h}\\
D=Z-N \label{59}\end{equation}$$
Siły w śrubach czołowego połączenia zwykłego wyznaczamy w sposób pokazany w artykule Połączenia śrubowe.
Naroża ram pełnościennych
Rodzaje naroży ram pełnościennych
Szczególnym elementem ram blachownicowych są naroża, najczęściej połączenia słupów z ryglami. Na rys. 38 pokazano miejsca wsystępowania rozmiatych naroży dżwigarów blachownicowych .
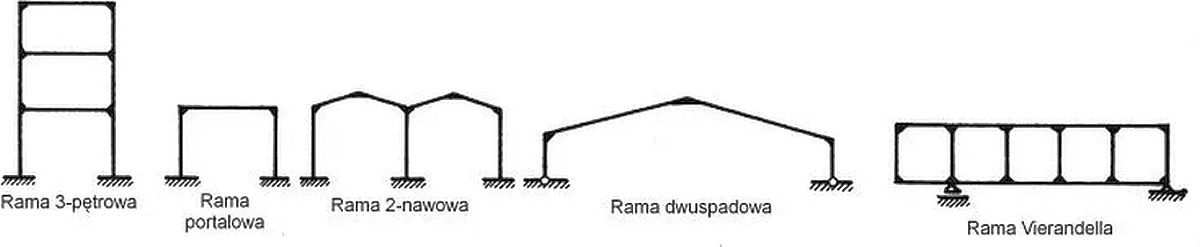
Rys.38 Typy ram blachownicowych i odpowiadające naroża ram [13]
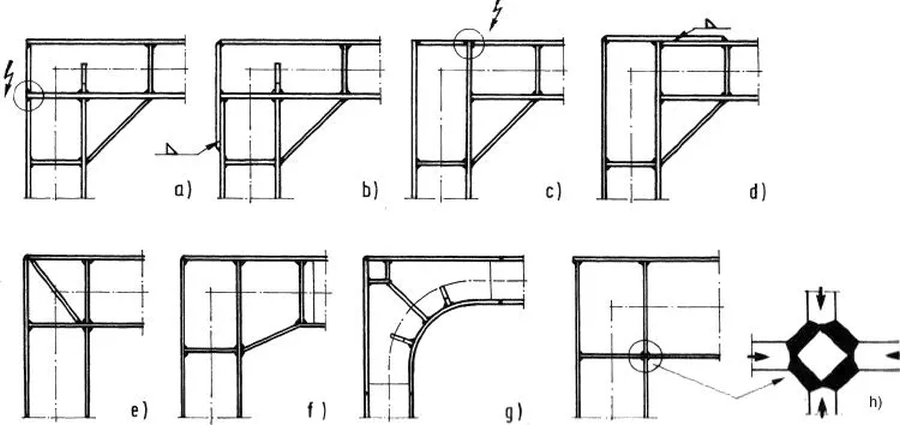
Rys.. 39 Przykłady konstrukcji naroży ram [13], str. 750
Naroża pokazane na rys. 39a)-d) są wzmocnione od dołu elementem blachownicowym i użebrowane poprzecznie na ryglu i słupie. środnik w narożu 39 e) posiada żebro ukośne. Naroże 39 f) łączy słup z blachownica o zmiennej wysokości. Naroże 39 g) jest wyokrąglone i stosownie użebrowane. Na rys. 39 h) wskazano na punkt krytyczny naroża, w którym łączy się szereg rozciąganych blach.
Żebrowanie naroży
Ze względu na możliwość rozwarstwienia rozrywanych blach (rys. 40a) zaleca się stosowanie rozwiązań rys. 40b). W celu uniknięcia spiętrzenia naprężeń spawalniczych zaleca się stosowanie wycięć wyokrąglonych wycięć, np. pokazanych na rys. 41.
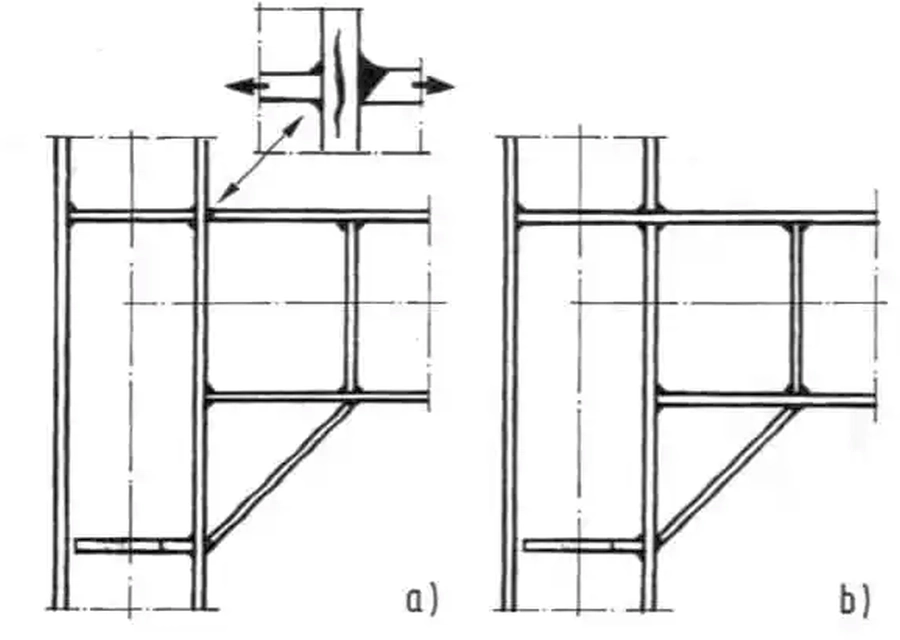
Rys.40 Konstruowanie naroża ze względu na rozwarstwienie [13]-str. 751
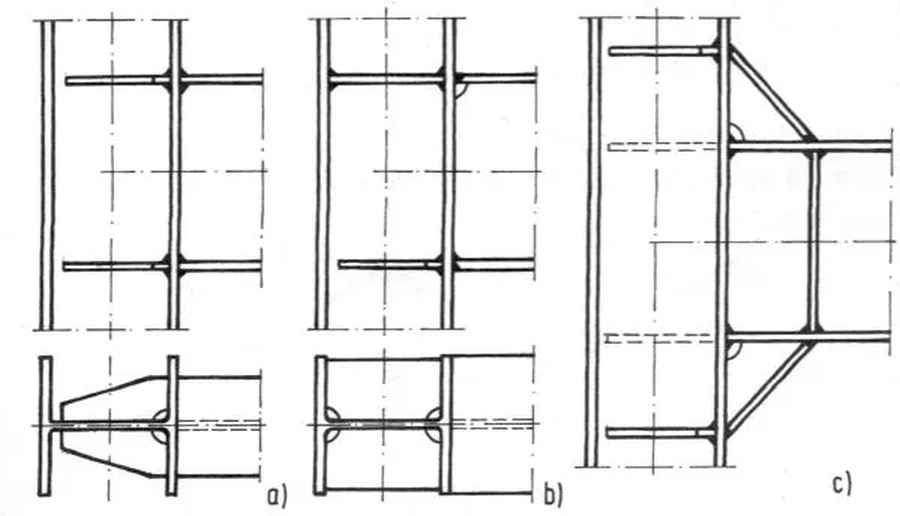
Rys.41 Konstruowanie wycięć w narożach ram [13]-str. 751
Rozmaite przykłady żebrowania poprzecznego naroży pokazano na rys. 42.
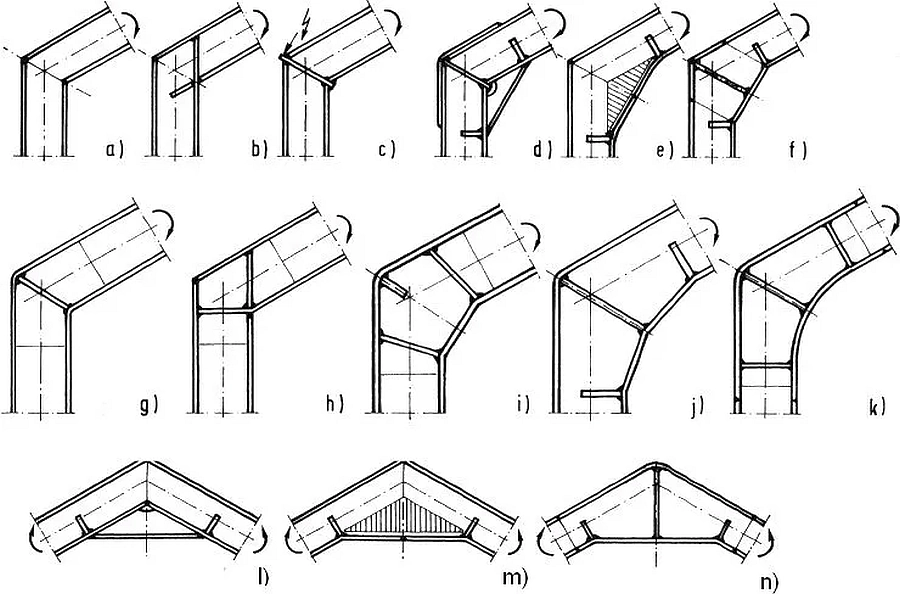
Rys.42 Przykłady żebrowania poprzecznego naroży ram [13]-str. 752
Sposób wyznaczania sił w żebrach pokazano na przykładzie naroża rys.43.
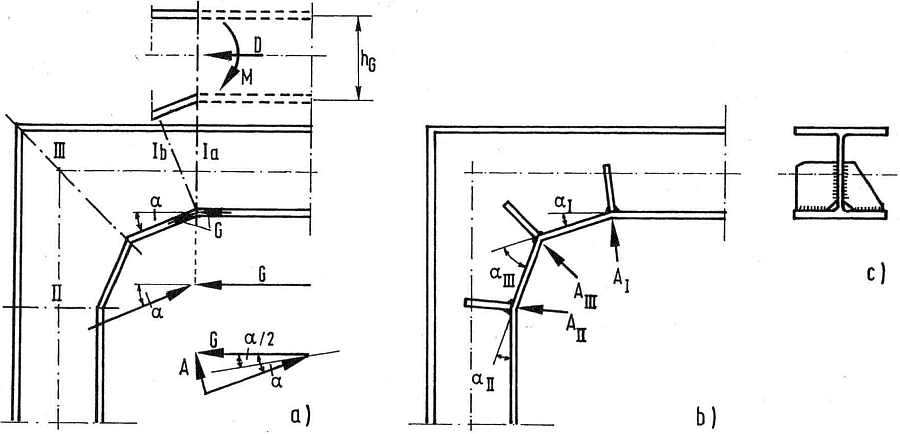
Rys.43 Przykład wyznaczania sił w żebrach (opis w tekście) [13]-str. 752
Rozpatrzmy naroże, pokazane na rys. 43. W ryglu działa siła osiowa $D$ oraz moment zginający $M$. W przekroju $I-I$ w pasie dolnym działa sila $G$, którą można oszacować z klasycznej zależności:
$$\begin{equation} G=\cfrac{D}{2}+\cfrac{M}{h_G} \label{60} \end{equation}$$
gdzie $h_G$ jest wysokością rygla w osiach pasów. Kąt pochylenia pochyłych części naroża wynosi $\alpha$. Wobec tego siła działająca na żebro umieszczone w narożu wynosi:
$$\begin{equation} A=2G \sin{\frac{\alpha}{2}} \label{61} \end{equation}$$
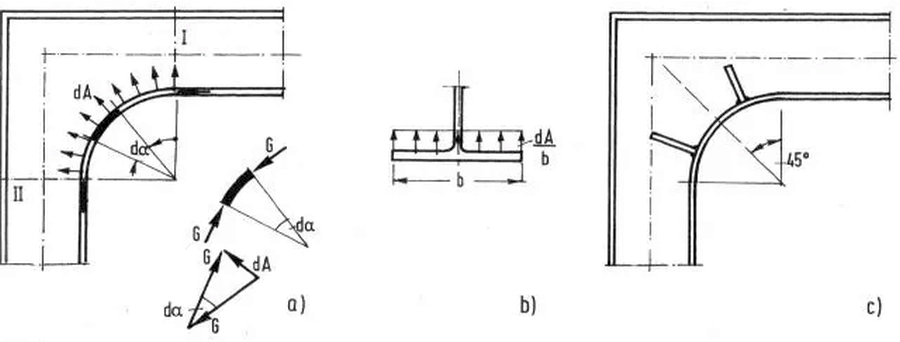
Rys.44 Wyznaczania sił w narożu wyokrąglonym (opis w tekście) [13]-str. 752
W przypadku naroża wyokrąglonego, pokazanego na rys. 44 mamy:
$$\begin{equation} dA=G\cdot d \alpha \label{62} \end{equation}$$
Wobec czego
$$\begin{equation} A \approx \int _{\alpha_R}dA =G \overline \alpha_R \label{63} \end{equation}$$
Tutaj $\overline \alpha_R$ jest obszarem wpływu żebra. Dla $\alpha_R=45 ^{\circ}$ jest $\overline \alpha_R=\frac{\pi}{4}$.
Wówczas $A= G \cfrac{\pi}{4}$.
Pola ciągnień i nośność nadkrytyczna
Podstawową współczesną teorią nośności smukłych środników blachownic: jest teoria pola ciągnień i nośności pokrytycznej środnika.
Zjawisko to zostało przedstawione w Polsce w pracy [18], poprzedzającej rozprawę habilitacyjną [19]. Rys historyczny i wybrane wyniki badań zmierzające do określenia nachylenia zastępczych krzyżulców (pola ciągnień), przedstawiono na rys.45.
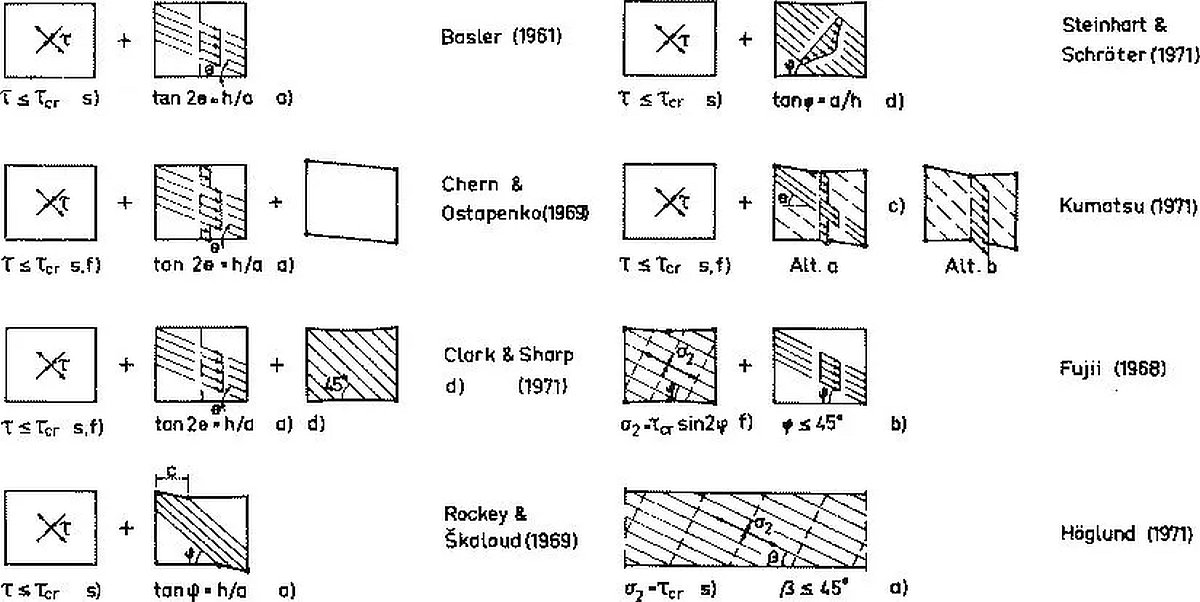
Rys. 45 Wybrane badania pola ciągnień: a) kryterium płynięcia Misesa, b) kryterium płynięcia Treski, c) dwa alternatywne pola ciągnień, d) blachownica aluminiowa, s) belka jednoprzęsłowa, f) belka zabezpieczona przed obrotem, s)f) sprężyste stężenia [20]
Badania prowadzone w latach 1961-1971, doprowadziły do ujęcia metody w rozdz. 5.2. [14] i sformułowania formuł obliczeniowych
Panele środnika blachownic po utracie stateczności są w stanie wytrzymać obciążenia znacznie przekraczające początkowe obciążenie krytyczne. W panelu dźwigara ograniczonym żeberkami po wyboczeniu tworzą się tak zwane ” pola ciągnień”, pokazane na rys. 46.

Rys. 46 Pola ciągnień w stanie pokrytycznym środnika [10]
Pole ciągnień wywołuje zmiany mechanizmu pracy dźwigara upadabniając jego pracę do pracy kratownicy zastępczej. Pasy kratownicy zastępczej to pasy blachownicy, słupki kratownicy to żeberka, a krzyżulce to właśnie utworzone w środniku blachownicy pola (pasy) ciągnień. Kratownicę zastępczą pokazano na rys.48 .
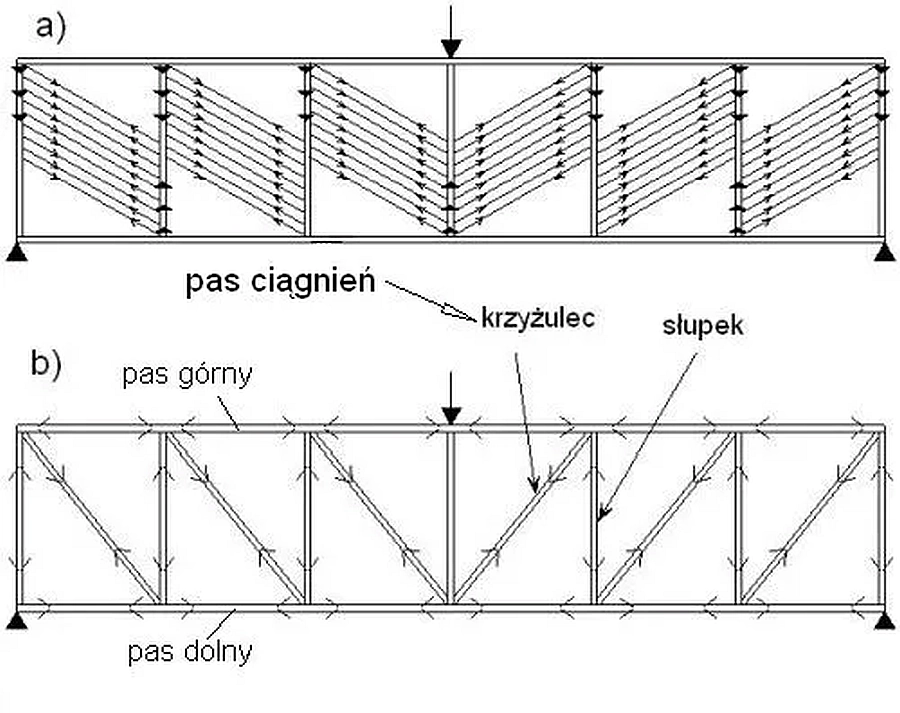
Rys.47 Analogia kratownicowa nośności blachownicy a) pole (pas) ciągnień; b) zastępcza kratownica Pratta lub typu N [10]
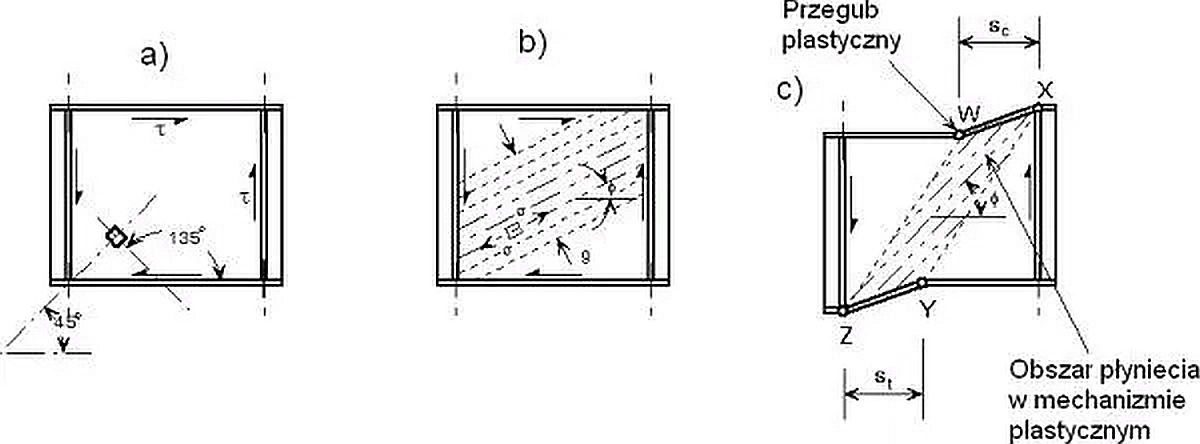
Rys. 48. Mechanizm zniszczenia środnika blachownicy: a) stan przedwyboczeniowy, b) stan pokrytyczny, c) mechanizm zniszczenia pasów [10]
Mechanizm zniszczenia blachownicy, pokazany na rys.22 wskazuje na następujące zjawiska:
2) Po wyboczeniu środnika pojawiają się pola ciągnień (rys. 10b), które realizują kratownicowy mechanizm zniszczenia,
3) dopiero po załamaniu pasów na skutek wytworzenia przegubów plastycznych (rys. 10c) nośność belki jest wyczerpana.
Nośność blachownicy mierzona siłą poprzeczną $V_{b,Rd}$ jest sumą nośności środnika $V_{bw,Rd}$ (rys. 16a+b) i pasów $V_{bf,Rd}$ (rys. 16c).
Nośność środnika $V_{bw,Rd}$ w formie zgodnej z normą [14] może być zapisana w postaci [10] poprzez sumę sprężystej nośności krytycznej (rys. 14a) $V_{b,Rd,cr}$ i nośnosci pokrytycznej $V_{b,Rd,pcr}$ , wynikającej z pasa ciągnień (rys. 14b):
$$\begin{equation} V_{bw,Rd}=V_{bw,Rd,cr}+V_{bw,Rd,pcr}\\
V_{bw,Rd,cr}= \cfrac {h_w \cdot t_w \cdot \tau_{bb}} {\gamma_{M1}}\\
V_{bw,Rd,pcr}= 0,9 \cdot g \cdot t_w \cdot \cfrac{\sigma_{bb}} {\gamma_{M0}} sin \varphi\\
\label{64} \end{equation}$$
gdzie zgodnie z rys. 14b: $g = h_w cos \varphi – (a – s_c – s_t) sin \varphi$, a $s_c$ i $ s_t$ określają położenie przegubów plastycznych w pasach. Położenie przegubów jest wyznaczane jako położenie maksymalnego momentu zginającego belkę , to znaczy dla punktu zerowego ścinania, jak następuje[21]:
$$\begin{equation}S= \frac{2}{sin \Phi} \sqrt{\frac {M_{f,Rk}}{t_w} \sigma_{bb}} \le a \label{65}\end{equation}$$
gdzie $M_{f,Rk}$ jest nośnością charakterystyczną pasów.
Pole ciągnień (rys. 14b) jest rozwijane przy nachyleniu $\Theta$ do poziomu. Dalszy wzrost obciążenia prowadzi do uplastycznienia pasów przez naprężenia $\sigma_{bb}$, określone z hipotezy Hubera-Misesa [21]:
$$\begin{equation}\sigma_{bb}=\frac{1}{2}\sqrt {f_{yw}^2-3\tau_{bb}^2+\Phi^2}-\Phi \label{66}\end{equation}$$
gdzie wprowadzono parametr pomocniczy $\Phi=1,5 \tau_{bb} sin 2 \varphi$
Na rys. 16a zilustrowano sytuację przedwyboczeniową, którą reprezentuje pierwszy człon w równaniu (24). Sprężyste naprężenia krytyczne $\tau_{bb}$ (20) są wyznaczane wg sprężystej teorii wyboczenia , w sposób przedstawiony na rys.49.
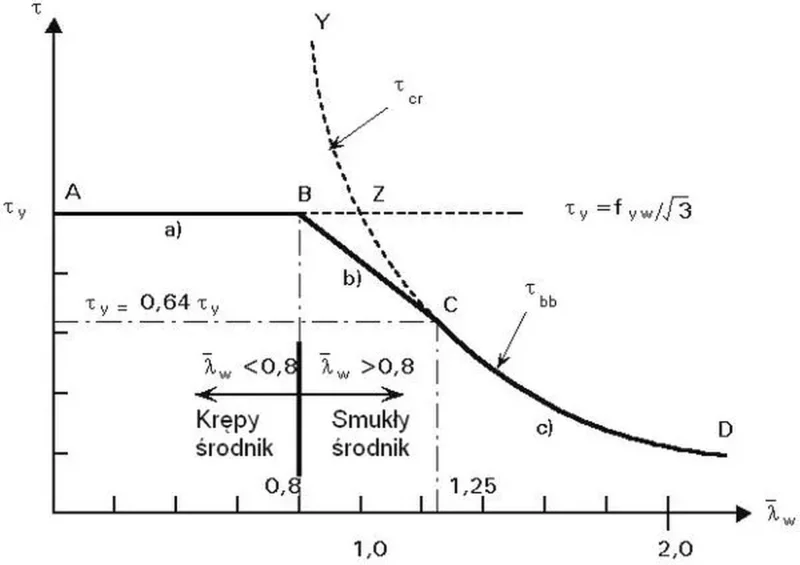
Rys.49 Sprężyste naprężenia krytyczne w panelu środnika [10]
$$\begin{equation} \tau_{bb}= \begin {cases}
\cfrac{f_{yw}}{\sqrt{3}} & \textrm { dla } \overline \lambda_w < 0,8 & \textrm {( krępy środnik na odcinku A-B) } \\
[1 – 0,8 \cdot ( \overline \lambda_w – 0,8)] \cdot \cfrac {f_{yw}}{\sqrt{3}} & \textrm { dla } 0,8 \le \overline \lambda_w < 1,25 & \textrm {( średni środnik na odcinku B-C}) \\
\cfrac {1} {\overline \lambda_w^2} \cfrac {f_{yw}}{\sqrt{3}} & \textrm { dla } overline \lambda_w \ge 1,25 $ & \textrm {( smukły środnik na odcinku C-D}) \\
\end {cases} \label{67}\end{equation}$$
gdzie:
$f_{yw}$ – granica plastyczności stali środnika $ (w)$,
$\overline \lambda_w= \cfrac{\lambda_w} {\lambda_1} $ – smukłość względna środnika, będąca stosunkiem smukłości
$\lambda_w= \frac{h_w}{t_w}$ oraz smukłości względnej $\lambda_1 $ zależnej od wytrzymałości stali środnika wg [11].
Smukłość porównawczą wyznacza się w sposób klasyczny, analogicznie jak w przypadku innych postaci wyboczenia.
Wszystkie zmienne wymagane przy do oszacowania nośności środnika (17) łącznie z kątem $\varphi$ nie są znane. Kąt $\varphi$ nie może być wyznaczony bezpośrednio, tylko w procedurze iteracyjnej, powtarzanej dopóty, dopóki nie uzyskamy $\varphi$ zapewniającego maksymalną nośność na ścinanie $ V_{bb,Rd}$. Zbieżność procesu nie jest szybka. Prawidłowa wartość $\varphi$ zawiera się pomiędzy $\frac {\Phi}{2}$ (minimum – rys. 24a), a $\Phi$ (maksimum- rys 24b). Studium przeprowadzone przez [11] dla zwykłych proporcji blachownic wskazuje, że maksymalna nośność na ścinanie jest uzyskiwana dla:
$$\begin{equation} \varphi \approx \frac{\Phi}{1,5} \label{68}\end{equation}$$
Przyjęcie takiej wartości $\varphi$ może dać prawidłowe oszacowanie nośności$ V_{bb,Rd}$, a w każdym razie oszacowanie bezpieczne i jest dobrą wartością startową do iteracji.
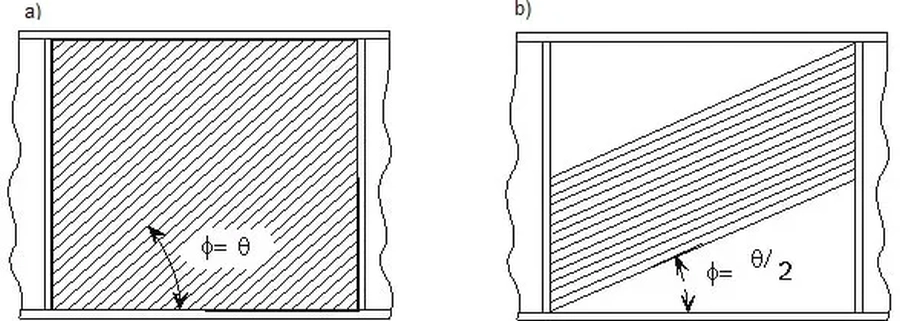
Rys. 50. Graniczne przypadki kąta $\varphi$: a) minimum – ciągnięcia „tylko w środniku” , b) maksimum – ciągnięcia „całego panela”[10]
Połączenia ram z profili giętych na zimno
Na rys. 51 w celu przekierowania czytelnika do dżwigarów i hal produkowanych z profili giętych na zimno – pokazano przykładowy detal połączenia słupa z ryglami i belkami (płatwiami) hali wykonanej z profili giętych typu 2x∑.
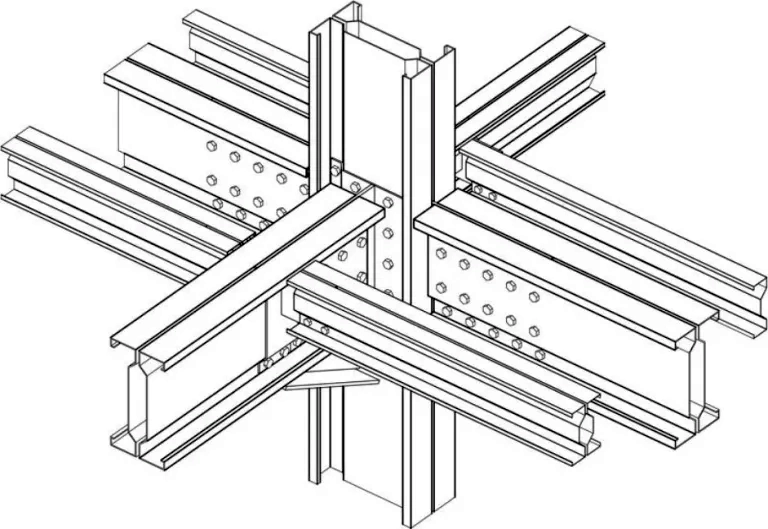
Rys.51. Połączenie słupa z ryglami i belkami z profili giętych 2∑ ((ArcelorMittal Distribution, (2015). Purlins – Arclad Services,[ http://www.ruukki.com/~/media/Files/Lightweight-purlins/PDF/Ruukki-
Literatura
- Chodor L., (2016). Przekrycia hal i galerii. Materiały XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji, Tom I, ss. 25–202, [ https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf]
- ArcelorMittal Sections, (2015). Poradnik Projektanta. Konstrukcje Stalowe w Europie, [ http://sections.arcelormittal.com/pl/biblioteka/poradnik-projektanta-konstrukcje-stalowe-w-europie.html ]
- Astron (2015). Steel buildings – Technical details of Astron steel buildings – Astrin steel buildings, [ http://www.astron.biz/en/technical-details/index.html ]
- Butler, S. (2015). Classic II Building System, [ http://butlermfg.com/en/products_systems/structural_systems/classic_ii_building_system ]
- Kucharczuk W., Labocha S. (2012). Hale o konstrukcji stalowej. Poradnik projektanta. Polskie Wydawnictwo Techniczne
- Kucharczuk W. (2014). Ramy pełnościenne Przegląd rozwiązań konstrukcyjnych. Część I. Nowoczesne Hale, 1(14), 21–23
- Zekon Z6 (2015), Realizacje Zekon, [ http://www.zekon.pl/pl/system-sin/przyklady/ ]
- Skalski, (2016). Hale stalowe system blachownicowy, [http://www.skalski.com.pl/pl/49/hale-stalowe-system-blachownicowy ]
- Kudła, A., Kuśmierczyk, M. (2016), Hala z kształtowników giętych na zimno. Analizy porównawcze z konstrukcją konwencjonalną. Politechnika Świętokrzyska w Kielcach
- Stiemer, S. F. (2016). Advanced Structural Steel Design. Plate Girders. Lecture CIVL432 The University of Britsch Columbia
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Medwadowski J. (Ed.). (1980). Konstrukcje metalowe i stalowe, PWN
- Petersen C. (2013), Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
- PN-EN 1993-1-5:2008, Eurokod 3: Projektowanie konstrukcji stalowych. Część 1-5: Blachownice
- PN-EN 1993-1-10:2005, Eurokod 3: Projektowanie konstrukcji stalowych. Część 1-10: Dobór stali ze względu na odporność na kruche pękanie i ciągliwość międzywarstwową
- Bródka J., Broniewicz M. (2013). Projektowanie konstrukcji stalowych według Euro-kodów. Podręcznik inżyniera. Polskie Wydawnictwo Techniczne
- Goczek J., Supeł Ł., Gajdzicki, M. (2011). Przykłady obliczeń konstrukcji stalowych: Eurokod 3-1-1, Eurokod 3-1-3, Eurokod 3-1-5, Eurokod 3-1-8. Wydawnictwo Politechniki Łódzkiej
- Kowal, Z. (1962), Dżwigary o cienkościennym srodniku, pracujące w stanie pozakry-tycznym. Inżynieria i Budownictwo, 10, 377–382
- Kowal Z. (1964). Dzwigary dachowe z żebrowaniem pionowym i przekątnym, Praca Habilitacyjna No. 97; Budowncitwo XXI). Politechnika Wrocławska
- Höglund, T. (1981), Design of thin plate I-girders in shear and bending with special reference to web buckling (Bulletin of the Division of Building Statics and Structural Engineering No. 94). The Royal Institute of Technology, Stockholm
- Narayanan R. (Ed.). (1983). Plated Structures;. Stability and Strength. Applied Sci-ence Publishers
________________________________