Euler jest twórcą teorii stateczności systemów sprężystych. W roku 1744 wyznaczył siłę krytyczną ściskanego słupa poprzez rozwiązanie ścisłego równania różniczkowego zgiętej osi pręta przegubowo opartego na końcach. W roku 1757 uzyskuje ten sam rezultat z wykorzystaniem zlinearyzowanego równania różniczkowego, W pracy zajmuje się statecznością słupa obciążonego siłami skupionymi $N$ na końcach oraz równomiernie rozłożonymi po długości siłami osiowymi $n$ (rys.1). Popełnił przy tym błąd, który został naprawiony dopiero 150 lat później w pracy [1].
Obciążenia zewnętrzne $N,n(z) $ wywołują moment zginający.
| $M(z)= – \int \limits_0^z n \cdot [v(z)-v(\zeta)] d\zeta \, – Nv(z)$, | (1) |
gdzie $v(z)$ jest ugięciem pręta w punkcie o współrzędnej $z$, a $ v( \zeta)$ – ugięciem w punkcie pośrednim $\zeta \in (o,z)$.
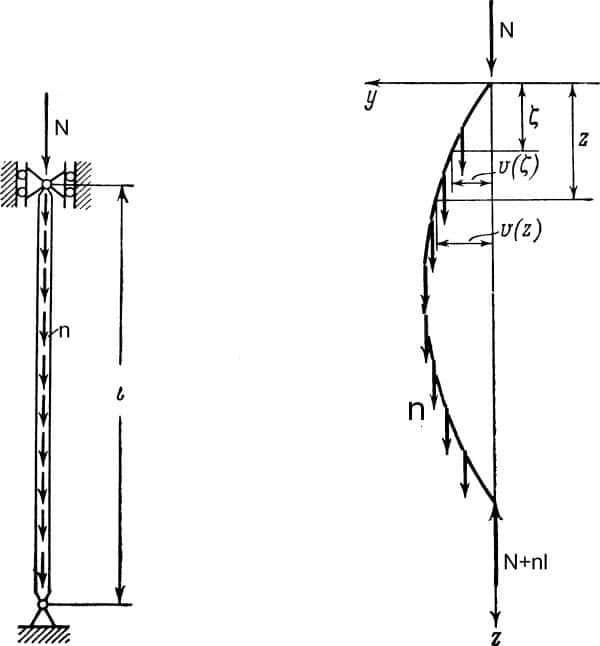
Rys.1. Schemat konstrukcji i obciążeń analizowany przez Eulera [2]
Z drugiej strony podstawowe równanie różniczkowe zginania wymusza:
| $M(z)= EI \dfrac{d^2 v}{dz^2}$, | (2) |
Z porównania (1) i (2) otrzymujemy równanie różniczkowe pręta z rys. 1:
| $EI \dfrac {d^2 v}{dz^2}+n \int \limits_0^z [v(z) -v(\zeta)] d \zeta \, +N \cdot v(z) \,= 0$, | (3) |
Po przekształceniu całki wchodzącej (3)w ten sposób, że
| $\int \limits_0^z [v(z) -v(\zeta)] d \zeta=v(z)-\int \limits_0^z v(\zeta) d \zeta= v(z)\cdot z -[\zeta v(\zeta) {|}_0^z + \int \limits_0^z \zeta \dfrac {dv}{d \zeta} d \zeta= \int \limits_0^z \zeta \dfrac {dv}{d \zeta} d \zeta$, | (4) |
to zamiast (3) otrzymamy:
| $EI \dfrac {d^2 v}{dz^2}+n \int \limits_0^z \zeta \dfrac{dv}{d \zeta} d \zeta \, +N \cdot v(z) \,= 0$, | (5) |
lub po przeróżniczkowaniu
| $EI \dfrac {d^3 v}{dz^3}+(n (z+N) \dfrac {d v}{dz} \,= 0$, | (6) |
Otrzymaliśmy znane obecnie, ale nie znane za czasów Eulera wyrażenie, które można prosto otrzymać z formuły na siłę poprzeczną w belce. Równanie (6) jest trzeciego rzędu, więc jego rozwiązanie musi mieć trzy stałe całkowania. Tymczasem rzeczywiste rozwiązanie zadania powinno spełniać cztery warunki brzegowe
| $v=0$ $\dfrac {d^v} {dz^2}$, dla $z=0$ i $z=l$ |
(7) |
Błąd Eulera był trywialny i polegał na zaniedbaniu ostatniego warunku brzegowego (7), co można dopuścić tylko dla przypadku małego $n$, wskutek czego Euler otrzymał prawidłową wartość siły krytycznej $N_{cr}$ w dla przypadku granicznego $n=0$.
W 1778 roku pokazany błąd, polegający na analizie równania (6), ale bez działania siły $N$ na wierzchołku słupa (rys.1) doprowadził do paradoksu, polegającego na wynika, że taki słup nie może utracić stateczności. Zjawisko nieograniczonej stateczności słupa obciążonego ciężarem własnym sam Euler nazywa „nie tylko paradoksem, ale i bardzo podejrzanym”.
W kolejnej publikacji w 1778 roku Euler wyjaśnił paradoks poprzez uwzględnienie w rozwiązaniu poziomej reakcji H (rys.2).
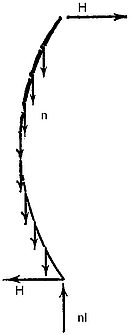Rys.2. Prawidłowy układ sił równowagi słupa pod ciężarem własnym $n$ [2]
W miejsce równania problemu (6) otrzymaliśmy równanie prawidłowe (8) [2]:
| $EI \dfrac {d^3 v}{dz^3}+(n (z+N) \dfrac {d v}{dz} \,= H$, | (8) |
Literatura
- Dinnik, A. N. (1935). Ustojcivost uprugich system, Objedinnoje Naucno-Techniceskoje izdatelstwo NKTP SSSR, [http://dwg.ru/lib/800]
- Panovko J., G., Gubanova, I. I. (1967), Ustojčivost i kolebanija uprugich system. Sovremennyje koncepcii, paradoksy i ošibki (4th ed.), Nauka, Moskva
________________________________
