Trwa remanent po dużej awarii portalu. Przepraszam za nieczytelną część treści do zakończenia remanentu !
Artykuł w ciągu ostatnich 24 godzin czytało 0 Czytelników
Chodor L., Belki żelbetowe,, cz.2 Przykłady rachunkowe, Encyklopedia πWiki, www.chodor-projekt.net, 13 lipca 2018 – marzec 2020
Przedstawiono przykłady rachunkowe do artykułu Belki żelbetowe. Wprowadzenie. Istotnym celem przykładów jest sprawdzenie skuteczności działania kalkulatora żelbetu CH-P Z i porównanie uzyskiwanych wyników ze znanymi przykładami opublikowanymi w literaturze specjalistycznej.
Zginanie proste
Belka stropu płaskiego zbrojona pojedynczo i konstrukcyjnie górą
Przykład [zotpressInText item=”{LUEPHEIJ,Przykład 4-1}”]
Zaprojektować zbrojenie belki żelbetowej swobodnie podpartej o przekroju prostokątnym obciążonej równomiernie pod długości, pokazanej na rys. 45.
Klasa ekspozycji XC2, klasa odporności ogniowej R60, klasa konstrukcji S4.
Rys. 45 Strop płytowo-belkowy: a) rzut, b) przekrój, c) belka stropowa
[zotpressInText item=”{LUEPHEIJ,Rys. 4-35}”]
Dane ogólne
Beton C20/25:
(tab.1) $\to$ $f_{ck}=20 \, MPa$ , $f_{cd}=20/1,4=14,3 \, MPa$
Stal B500: (tab.2) $\to$ $f_{yk}= 500 , MPa$, $f_yd=500/1,15=435 \, MPa$
Długość belki w świetle murów $l_n=5,0 \, m$,
Grubość muru z lewej $t_l=500 \,$mm
Grubość muru z prawej $t_p=500 \,$mm
Długość obliczeniowa belki (2) $\to l_{ef} =5,0+[1]$ ),
gdzie końcowy współczynnik pełzania $ \varphi ( \infty \, , 28) =2,759 $ wyznaczono w zakładce „Pełzanie” arkusza CH-P Ż.
Schemat obliczeniowy belki
Belkę podzielono na 20 elementów o długości $dx= 6000/20=30 \, mm$ każdy
Macierze współczynników różnicowych A i odwrotna $A^{-1}$
Dla 20-tu elementów różnicowych macierz współczynników różnicowych przedstawiono w tab.14. Macierz odwrotna $A^{-1}$ ma współczynniki zestawione w tab.15. W arkuszu CH-P Ż stosuje się podział właśnie na 20-ścia elementów różnicowych, skąd wynika, ze macierze $A$ i $A^{-1}$ w tab. 14 i 15 są takie same dla każdego zadania rozwiązywanego w kalkulatorze.
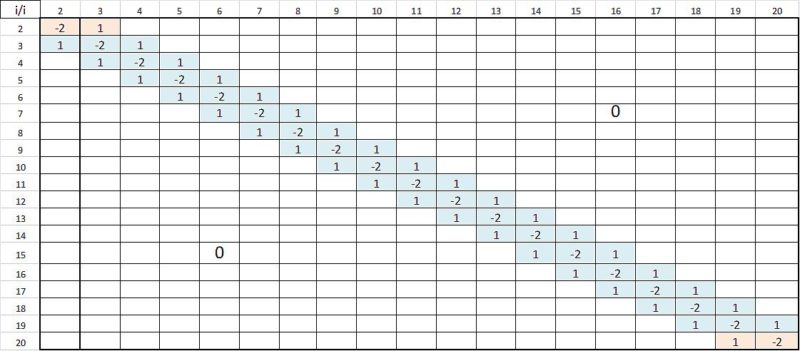
Tab.14 Macierz współczynników różnicowych dla liczby elementów n=20 (liczba równań n+1-2= 19)
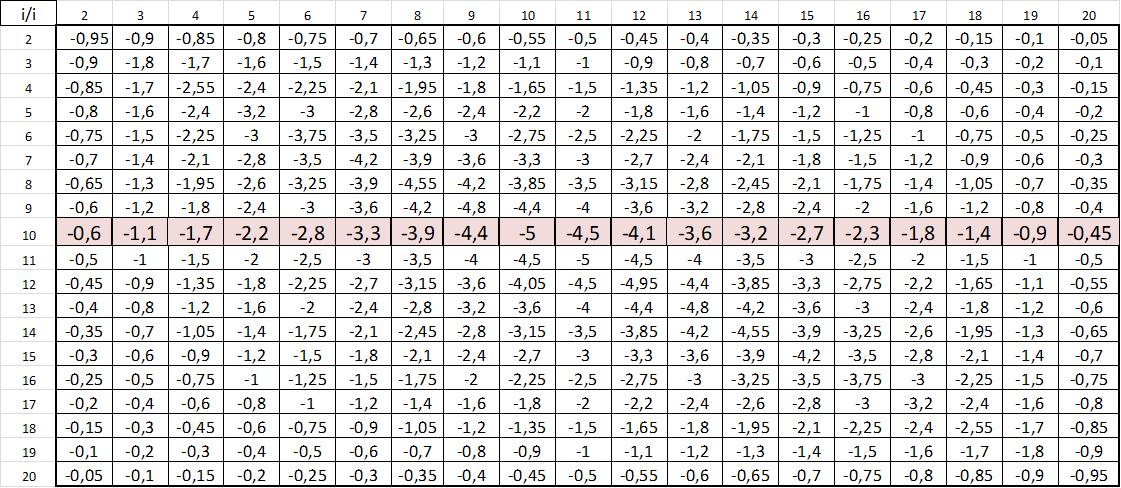
Tab.15. Macierz odwrotna współczynników różnicowych dla liczby elementów n=20
Wektor obciążeń równania kanonicznego
Wektor obciążeń różnicowych ($ \ref{187}$) wyznaczamy dla danego pola momentów zginających w każdym węźle. Poniżej dla przykładu wyznaczymy jeden wyraz wektora $|P|$ dla miejsca maksymalnego momentu zginającego, czyli dla i=10 (x=0,3\cdot (10-1)= 2,70 \, m) , to znaczy tuz przed środkiem rozpiętości belki.
Rzeczywisty rozkład momentów zginających
Rzeczywisty rozkład momentów zginających odczytano z rozwiązania belki metodą MES (opcja MES-20 pkt w kalkulatorze CH_p Ż).
Dla rzędnej $x=2,70 \, m$ z obliczeń statycznych mamy (tab. 13):
od obciążeń obliczeniowych $M_{max, Ed} =114,45 \, kNm$
od obciążeń z kombinacji charakterystycznej częstej $M_{max, Ek}=0,6327 \cdot 114,5 =72,41 \, kNm$
Ponieważ M=72,41 > M_{cr} = 12,79 \, kNm, to odpowiadające obciążenie różnicowe wyznaczamy w stanie po zarysowaniu dla $I_{II}=52985 \, cm^4$
Po uwzględnieniu wpływu skurczu, moment miarodajny moment zginający w węźle do obliczania ugięć wyniesie
($\ref{179}$) $\to$ $M(2,70) = 72,41+6,31 = 78,72$,
$\to$ $ |F_r| = – 0,3^2 / 8,8 \cdot 78,72 / 53026 \cdot 10^5=1,52 \, mm$
Po obliczeniach dla wszystkich węzłów otrzymamy wektor zestawiony w tab.16.
Tab.16. Wektor obciążeń różnicowych $|F_{r,real}|$ od obciążeń w opcji „MES” (obciążeń rzeczywistych)
Zastępczy rozkład momentów zginających
Zastępczy rozkład momentów zginających wyznaczono w sposób pokazany na rys. 40 dla obciążenia zastępczego $q_z=35,43 \, kN/m$ (opcja $M_L-M_max M_0$ w kalkulatorze CH_p Ż)
Po obliczeniach dla wszystkich węzłów otrzymamy wektor zestawiony w tab.17.
Tab.17.Wektor obciążeń różnicowych |F_{r,real| od obciążeń w opcji „$M_L-M_max M_0$” (obciążeń zastępczych)
W przykładzie różnice pomiędzy ugięciami z obciążeń rzeczywistych i zastępczych są niewielkie i dopuszczalne w praktyce.
Linia ugięcia zarysowanej belki
W tab.18 zestawiono linię ugięcia belki w opcji rzeczywistego rozkładu momentów. Porównano obciążenia różnicowe $F_{r*}$ i ugięcia belki niezarysowanej (elastic) i zarysowanej (crack). W przykładzie uzyskano 20% różnicy, przy czym oba typy ugięć wyznaczano po 50 latach pełzania betonu.
Tab.18 Ugięcia belki niezarysowanej (elastic) i zarysowanej (crack)
Strzałka ugięcia belki w stanie zarysowanym wyniesie $\delta = 60.6 \, mm$.
Literatura
[zotpressInTextBib style=”apa” sortby=”author” sort=”ASC”]Literatura
- 300+300)/2)/1000=5,3 \, m$.
Maksymalny moment przęsłowy $M_y= 182,8 \, kNm$
Dobór wstępny przekroju i zbrojenia belki
Wysokość belki (3) $\to h=l_{ef}/12=442 \to 450 \, mm$
Szerokość belki (4) $\to b=h/2=450/2=225 \to 250 \, mm$
Przyjęto pręty zbrojeniowe $\Phi=18 \, mm (A_{s1}=2,54 \, cm^2 ) $
Otulenie zbrojenia $c_{min}=\Phi=18 \, mm$,
$c_{dur}= 25 \, mm$ dla klasy ekspozycji XC2, $\Delta c_{dev}=10 \,mm $.(11) $\to$ $c= \max{[18;25]} +10=35 \, mm$
(12) $\to $ $a =35+18/2=44 \, mm$
Wysokość użyteczna przekroju $d=450-44=406 \, mm$
Wstępne szacunki pola przekroju zbrojenia:
(9) $\to$ dla zbrojenia podwójnego (górą i dołem)
$\Sigma A_s=A_{su}+A_{sl}\approx \dfrac {182,8} {435 \cdot (0,45-2\cdot 0,044)} \cdot 10^1=11,6 \, cm^2$= 5 $\Phi 18$,(10) $\to $ dla przekroju pojedynczo zbrojonego
$A_{sl} \approx \dfrac{182,8} {435 \cdot 0,9 \cdot (0,45-0,044) }\cdot 10^1=11,5 \, cm^2$= 5 $\Phi 18$,.Dobór zbrojenia metodą klasyczną MU
(27) $\to $ unormowany moment zginający $m_y= \dfrac{182,8}{ 0,25 \cdot 0,406^2 \cdot 14,3 \cdot 10^3}=0,310$,
(47) $\to $ względna wysokość strefy ściskanej $\xi= 1 – \sqrt{1 – 2 \cdot 0,310 / 1,0} =0,384$,
(48) $\to $ względne ramie sił wewnętrznych $\zeta = \tfrac{1}{2}(1+\sqrt{1-2 \cdot 0,310 / 1,0 }=0,808$,
- Zbrojenie dolne (pojedyncze)
(49) $\to $ $A_{sl,1} = \dfrac {0,310 \cdot 25 \cdot 40,6 \cdot 14,3} {0,808 \cdot 435}= 12,8 \, cm^2 = 6 \Phi 18$,
- Czy potrzebne zbrojenie podwójne
(44) $\to $ względny moment graniczny dla betonu zwykłego $m_u=0,251$,
(45) $\to $ warunek zbrojenia podwójnego $m_y= 0,310 >m_u=0,251 \to $ należy zastosować zbrojenie górne.- Zbrojenie górne
(50) $\to $ nadwyżka momentu zginającego $\Delta m= 0,310- 0,251=0,059$,
(51) $\to $ zbrojenie górne $A_{su,2}= \dfrac {0,059 \cdot 25 \cdot 40,6 \cdot 14,3}{ (1-44/406) \cdot 435} =0,15 \, cm^2 = 1 \Phi 18$,
(52) $\to $ zbrojenie dolne przy występowaniu górnego $A_{sl,2}= 12,8+1 \cdot 2,54=15,34 \, cm^2 = 7 \Phi 18$.Dobór zbrojenia kalkulatorem „CHP-Ż-1.3”
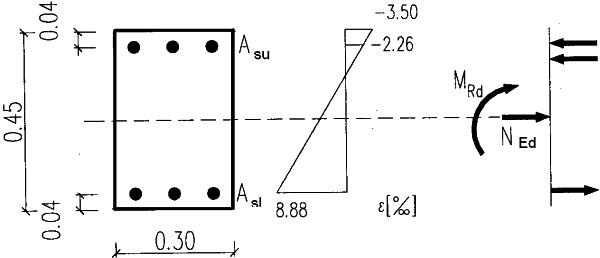
Dobór metodą MN ( nieliniowa aproksymacja naprężeń w betonie jest w kalkulatorze domyślna) pokazano na rys. 46. Czytelnik może sam sprawdzić obliczenia w arkuszu.
Rys.46. Ekran kalkulatora do przykładu 1.1
(kliknij , aby pobrać)
W wyniku obliczeń kalkulatorem wykazano, że zbrojenie dolne można wykonać z $4 \Phi 18$, a zbrojenie górne konstrukcyjnie $2 \Phi 14$.
Wytężenie tak zbrojonego przekroju wynosi 99,4%. Uzyskano oszczędności zbrojenia ok. 1- (1+7)/(2+4)=1/3
Wniosek: stosowanie obliczeń nieliniowych, np z wykorzystaniem prezentowanego arkusza pozwala na znaczne oszczędności stali w stosunku do uproszczonych obliczeń „ręcznych”. Znaczne zwiększenie nośności przekroju uzyskano również wskutek uwzględnienia zbrojenia górnego, które powinno być zakładane ze względów technologicznych (mocowanie strzemion)
Belka zbrojona podwójnie
[zotpressInText item=”{I354ZHTS,Przykład 6.1, 6.2}”]
Znaleźć nośność belki zginanej jednoosiowo o przekroju prostokątnym 450×300 mm wykonanej z betonu C25/30 .zbrojonej stalą 18G2A (B356) zbrojonej dwustronnie:
a) $A_{sl}=5\Phi 18$, $A_{su}=2 \Phi 12$
b) $A_{sl}= 8\Phi 25$, $A_{su}=2 \Phi 12$
Otulenie osiowe prętów wynosi $a=40 \, mm$, czyli otulenie powierzchniowe: $c_l=40-12/2=34 \, mm$ dla zbrojenia górnego i $c_u=40-18/2=31 \,mm$ dla zbrojenia dolnego w przypadku a) oraz $c_u=40-25/2=27,5 \,mm$ dla zbrojenia dolnego w przypadku b).
Uwaga : zgodnie z założeniami pracy [zotpressInText item=”{I354ZHTS}”] współczynnik materiałowy dla betonu ustawiamy na wartość $\gamma_c=1,5$
Wynik przykładu oryginalnego
a) $M_{Ed}=145,9 \, kNm$
b) $M_{Ed}=317,6 \, kNm$
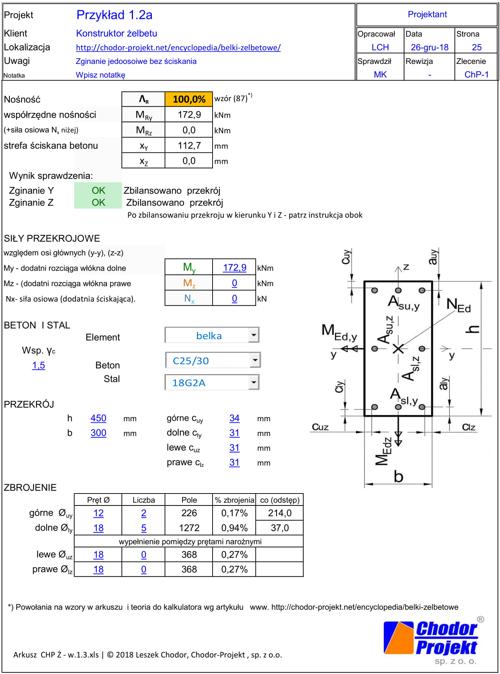
Dobór zbrojenia kalkulatorem „CHP-Ż-1.3”
Rys. 47. Ekran kalkulatora do przykładu 1.2a (kliknij , aby pobrać)
Arkusz z przykładem 1.2a można pobrać poprzez kliknięcie na rys. 45, arkusz z przykładem 1.2b tutaj.
Uzyskano wyniki:
a) $M_{Rd}=172,9 \, kNm$, czyli większą 172,9/145,9=1,19 razy
b) $M_{Rd}=352,1 kNm$, czyli większą 352,1 /317,6=1,11 razy
Wniosek: Stosowanie arkusza obliczeniowego pozwala na większe o kilkanaście procent obciążenie przekroju zginanego jednoosiowo w stosunku do obliczeń uproszczonych (przykład 1.2a) i ok 10% w stosunku do „ręcznych” obliczeń nieliniowych (prowadzonych iteracyjnie) w przypadku częściowego wytężenia stali (przykład 1.2b)
Zginanie ukośne względem jednej osi przypadek CT1
Nośność przekroju zbrojonego symetrycznie
[zotpressInText item=”{I354ZHTS,Przykład 6.3}”]
Dane geometryczne i materiałowe jak w przykładzie 1.2.
Rys. 48 Przekrój mimośrodowo ściskany CT
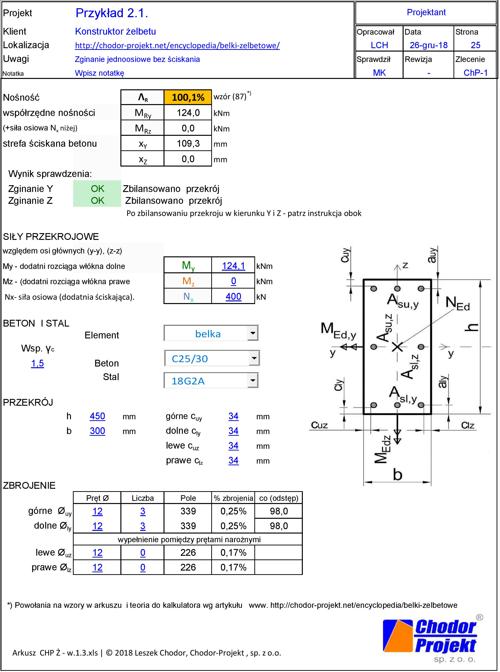
Znaleźć nośność mierzoną momentem zginającym$M_{Rd}$ przekroju ściskanego siłą $N_{Ed}=400 \, kN$ z rys. 48 zbrojonego górą i dołem $A_{sl}=A_{su}= 3 \Phi 12$
Wyniki z przykładu oryginalnego
$M_{Rd}=109,7 \, kNm$
Dobór zbrojenia kalkulatorem „CHP-Ż” (rys. 47)
Rys. 49. Ekran kalkulatora do przykładu 2.1. (kliknij , aby pobrać)
W arkuszu (rys.49) uzyskano nośność $M_{Rd}=124,1 \, kNm$ , czyli o $124,1/109,7=1,13 razy większą.
Nośność przekroju zbrojonego niesymetrycznie
[zotpressInText item=”{ZWDLNK2W,Prz. 13.1}”]
Dla przekroju 600×400 obciążonego siła osiową $N_{Ed}=2803 \, kN$ wyznaczyć zginający moment graniczny
Dane ogólne
C30/37- B500
h=600 mm, b=400 mm,$A_{sl}=10,74 \, cm^2$, (zbliżone pole 7Ø14)
$A_{su}=21,48 \, cm^2$, (zbliżone pole 14Ø14)osiowe otulenie zbrojenia $a_l=a_u=55 \,mm$, czyli $c_l=c_u=55-24/2= 16 \, mm$.
Podstawowe wyniki oryginalnego przykładu
Moment graniczny przekroju przy ściskaniu siła $N_{Ed}=2803 \, kN$ oszacowano na $M_{Rd}= 727,7 /, kN
Obliczenie nośności kalkulatorem „CCHP-Ż-1.3”
Po zadaniu siły osiowej $N_x= 2803 kN$ w kilku próbach uzyskano wytężenie 100% dla $M_y=764,5 \, kNm$ , czyli uzyskano nośność 764,5/727,7=1,05 razy większą (rys.50) .
Rys. 50. Ekran kalkulatora do przykładu 2.2. (kliknij , aby pobrać)
Zginanie ukośne względem dwóch osi przypadek CT2
Zbrojenie przekroju zbrojonego podwójnie zginanego ukośnie i ściskanego
[zotpressInText item=”{ZWDLNK2W,Przykład 13.6}”]
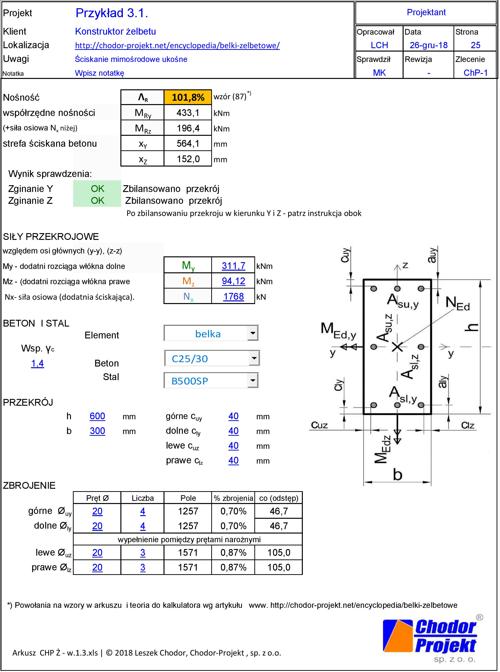
Rys.51 Przekrój ukośnie zginany do przykładu 3.1
Dane ogólne
C25/30 – B500
h=600 mm, b=300 mm, $\Phi_{max}=20$ mm,otulenie zbrojenia: $c=40 \, mm$, osiowe $a=c+\Phi/2=40+20/2=50 \, mm$
$d_{ly}=600-50=550 \, mm$, $d_{lz}=300-50=250 \, mm$,
$N_{Ed}=1768 \, kN$ kN,
$M_{Ed,y}=311,7 \, kNm$,
$M_{Ed,z}=94,12 \, kNm$
Uwaga:
- W wersji oryginalnej przykładu [zotpressInText item=”{ZWDLNK2W,Prz. 13.6}”]:
(a) momenty zginające oszacowano metodą nominalnej sztywności poprzez amplifikację momentów pierwszego rzędu $M_{Ed,y0}=200$ kN, $M_{Ed,z0}=60$ kN
(b) nośności przekroju mierzone momentami zginającymi w dwu kierunkach wyznaczono w interakcji z całkowitą siłą osiową i dla tego przypadku wyznaczono nośność przekroju mierzoną momentem zginajacycm
W oryginale przyjęto odwrotnie oznaczenia osi , tzn (y=z i z=y) - W niniejszym artykule:
(a) przyjęto, ze siły przekrojowe, w tym momenty zginające uzyskuje się bezpośrednio z obliczeń statycznych prowadzonych metodą II rzędu po obciążeniu całej konstrukcji siłami imperfekcji.
W rezultacie w każdym przekroju otrzymujemy amplifikowane siły przekrojowe bez potrzeby stosowania dodatkowych zabiegów, w tym wyznaczania długości efektywnych i współczynników wyboczeniowych pręta,
(b) nośności przekroju mierzone momentami zginającymi w dwu kierunkach wyznaczono w interakcji siłami osiowymi przydzielonymi proporcjonalnie do sztywności przekroju zgodnie z dwuetapowym algorytmem opisanym w ustępie Metoda rozprzężenia zginania ukośnego stosowana w arkuszu.
Podstawowe wyniki oryginalnego przykładu
Momenty graniczne wyznaczone z krzywych interakcji M-N (nomogramy w pracy [zotpressInText item=”{ZWDLNK2W}”]
$m_{Rdy}=0,33 \to M_{Rdy} = 0,33 \cdot 30 \cdot 55^2 \cdot 17,86 \cdot 10^{-3}=534,9 \, kNm$
$m_{Rdz}=0,276 \to M_{Rdz} = 0,276 \cdot 60 \cdot 25^2 \cdot 17,86 \cdot 10^{-3}= 184,9 \, kNm$
$n_{Ed}=\dfrac{1768}{ (30\cdot 60\cdot 17,86+12\cdot 3,14 \cdot 435) /10}=\dfrac{1768}{4854}=0,364$
Wykładnik interakcji w przykładzie oryginalnym przyjęto $a=1,24$
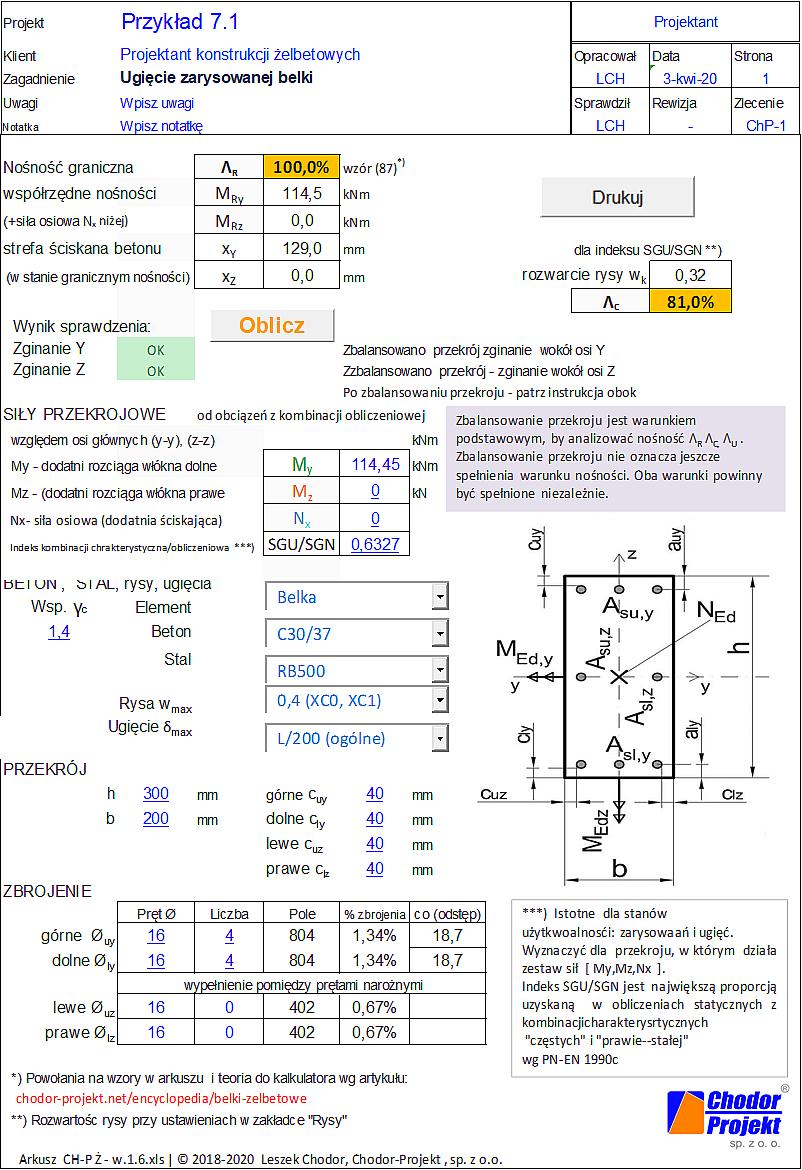
Wytężenie przekroju (87) $\to \Lambda_R = 94,5$ %.
Dobór zbrojenia kalkulatorem „CHP-Ż”
Na rys. 52 przedstawiono wyniki uzyskane w kalkulatorze „Belka żelbetowa CH-P zbrojenie”. W celu pobrania arkusza należy kliknąć na obraz. Po pobraniu i korekcie danych należy kliknąć na przycisk „Sprawdź” u góry arkusza. Nastąpi automatyczne zbalansowanie przekroju dla wybranego zbrojenia.
Obliczenia przeprowadzone w kalkulatorze wykazały, że układ zbrojenia dobrany w [zotpressInText item=”{ZWDLNK2W,Przykład 13.6}”] jest nieprawidłowy. Dla dobranego tam zbrojenia wytężenie przekroju przekroczone byłoby 3. krotnie, a decyduje o tym zginanie w kierunku Z , a nie Y : w kierunku X (mniejszej sztywności) należałoby dać 2+3=5Ø20 (a nie 2+1=3) – wówczas wytężenie wyniosłoby 95,1%.
Optymalne zbrojenie dobrane klakulatorem: w kierunku Y 4Ø20, w kierunku Z 2+3=5Ø20. Wówczas wytężenie wyniesie 101,8 % , czyli przekroczy nośność, ale tylko o 2%, co jest dopuszczalne.
Rys. 52. Ekran kalkulatora do przykładu 3.1 (kliknij , aby pobrać)
Wniosek: Projektowanie przekroju według algorytmu przedstawionego w [zotpressInText item=”{ZWDLNK2W,Przykład 13.6}”] może prowadzić do zdecydowanie zbyt małego i niepoprawnie rozłożonego zbrojenia.
Nośność przekroju zginanego ukośnie zbrojonego pojedyńczo
[zotpressInText item=”{I354ZHTS,Przykład 6.18}”]
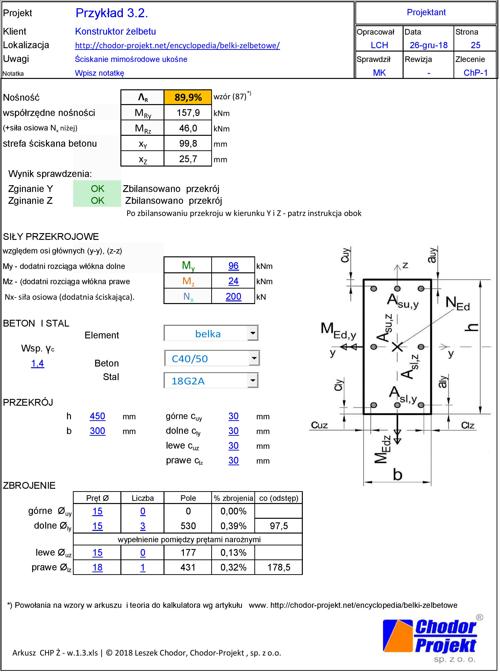
Sprawdzić nośność przekroju ukośnie zginanego, pokazanego na rys. 53: 450×300 C40/50-18G2A zbrojonego pojedynczo 3Ø15 (530 mm2), obciążonego siła ściskającą $N_{Ed}=200 \, kN$ działającą na mimośrodzie pionowym $ e_z=-0,48 \, m$ i poziomym $e_y=0,12 \, m$. Momenty zginające wynoszą więc: $M_{Ey}=200 \cdot 0,48=96,0 \, kNm$, $M_{Ez}=200 \cdot 0,12=24,0 \, kNm$
Rys.53 Przekrój ukośnie zginany
(zmodyfikowane [zotpressInText item=”{I354ZHTS,Rys 6.37}”]
Dobór zbrojenia kalkulatorem „CHP-Ż-1.3”
Podstawowe wyniki oryginalnego przykładu
W pracy [zotpressInText item=”{I354ZHTS”] przeprowadzono ścisłą analizę przypadku w sposób pokazany na rys. 54. W wyniku obliczeń iteracyjnych w tej pracy uzyskano strefę ściskaną rozprzestrzenioną wokół lewego, górnego naroża przekroju, a nośność przekroju $M_{Rd}=\sqrt{M_{Rdx}^2+M_{Rdy}^2}=135,1 \, kNm$
Rys. 54. Ekran kalkulatora do przykładu 3.2 (kliknij , aby pobrać)
Projekt wykonany kalkulatorem (rys.50) wykazał, że wystarczające jest zbrojenie dolne 3Ø15, ale w celu przeniesienia momentu $M_{Ez}$ koniczne jest zbrojenie prawe 1Ø18 (+ 1Ø15 ze zbrojenia w kierunku Y). Nośność tak zbrojonego przekroju wynosi: $M_{Ry}=157,9 \, kNm$ , $M_{Rz}=46,0 \, kNm$ (i $N_{Rx}=200 \, kN$. Wypadkowy nośność $M_R=\sqrt{157,9^2+46^2}=164,5 \,kNm$. Nośność wykazana w przykładzie oryginalnym stanowi 135,1/164,5= 82% nośności obliczonej w kalkulatorze. Zauważmy jeszcze, że zbrojony w kalkulatorze przekrój jest wytężony siłami zewnętrznymi tylko w 90%.
Ścinanie
Małe ścinanie
[zotpressInText item=”{M2MGDAP4,Lecture3/24}”]
Korzystamy z algorytmu przedstawionego na rys.27
Wyznaczyć zbrojenie poprzeczne belki ścinanej siłą poprzeczną $V_{Ed}$=705 kN.
Belka o przekroju hxb=1000×450 wykonana z betonu C30/37- B500: ($f_{ck}=500\, MPa,$ $f_{yd} =500/1,15=435 \, MPa$.
Otulenie osiowe zbrojenia dolnego a=66 mm, wysokość efektywna przekroju $d=1000-66=934 \, mm$Naprężenia ścinające
(92) $\to $ $v_{Ed} = \cfrac{V_{Ed}} {b_w \cdot 0,9 \cdot d}= \cfrac{705}{450 \cdot 0,9 \cdot 934} \cdot 10^3= 1,68 \, MPa$
Z tab 10 odczytujemy dla betonu C30/37 $\to$ $v_{Rd,max}(ctg \Theta=2,5)= 3,90 \, MPa$
Ponieważ $v_{Rd, max} = 3,901 \, > \, 1,68 \, MPa \to ctg \Theta=2,5$.
Przekrój zbrojenia poprzecznego
(112) $\to $ $A_{sw}/s=\cdot {1,68 \cdot 450}{435 \cdot 2,5}=0,70 \, mm^2/mm$
Przyjęto strzemiona Ø 10, 4-cięte: $A_{sw} = 4 \cdot \cfrac{\pi\cdot 10^2}{4}= 314 \, mm^2$Rozstaw strzemion $s \, < 314/0,70=448 \, mm \to$ przyjęto $s=440 \, mm$
Wymagany maksymalny rozstaw zbrojenia poprzecznego
(96) $\to $ $ s_{l,max}= 0,75\cdot 934= 700 \, > 440 \, mm$
(99) $\to $ $ s_{l,max}=12,5 \cdot \cfrac{314\cdot 500}{450 \cdot \sqrt{30}}=796 \, > 440 \, mm$
Większe ścinanie
[zotpressInText item=”{M2MGDAP4,Lecture3/26}”]
Korzystamy z algorytmu przedstawionego na rys.27
Wyznaczyć zbrojenie poprzeczne dla belki ścinanej siłą poprzeczną $V_{Ed}$=312,5 kN, przekroju hxb=550×140 , wykonanej z C30/37-B500
Otulenie osiowe zbrojenia dolnego a=50 mm, wysokość efektywna przekroju $d=550-50=500 \, mm$(92) $\to $ $v_{Ed} = \cfrac{312,5}{140 \cdot 0,9 \cdot 500} \cdot 10^3= 4,96 \, MPa$
Z tab 10 odczytujemy dla betonu C30/37 $\to$ $v_{Rd,max}(ctg \Theta=2,5)= 3,90 \, MPa$; $v_{Rd,max} (ctg \Theta=1,0)= 5,66 \, MPa$ , $\nu_1=0,528 $, $f_{cd}=
Zachodzi $ 3,90 \, < \, v_{Ed}=4,96 \, < \, 5,66 \, MPa \to $ należy wyznaczyć $\Theta$.
Kąt nachylenia krzyżulca betonowego
(111) $\to $ $ \Theta= 0,5 \cdot arcsin (2\cdot 4,96/(0,528\cdot 21,4 )=0,5358 rad=30,7^o \to ctg \Theta= 1,684 $
Wymagane zbrojenie poprzeczne
(112) $\to $ $A_{sw}/s=\cdot {4,96 \cdot 140}{500 \cdot 1,684}= 0,765 \, mm^2/mm$
Przyjęto strzemiona Ø 10, 2-cięte: $A_{sw} = 4 \cdot \cfrac{\pi\cdot 10^2}{4}= 157 \, mm^2$
Rozstaw strzemion $s \, < 157/0,765=205 \, mm \to$ przyjęto $s=200 \, < 0,75 \cdot 500=375 \, mm$
Strzemiona w tym rozstawie należy ułożyć od lica podpory na długości $l_w=z \cdot ctg \Theta= 0,9 \cdot 500 \cdot 1,684= 758 \,mm$,
Przyjęto $l_w= 4 \cdot 200= 800 \, mm$.
Na pozostałej części belki strzemiona można rozstawić w odległości l < 0,75 \cdot 500=375 \, mm$.Strzemiona i pręty odgięte
[zotpressInText item=”{FWPXIWD5,Prz.16.6}”]
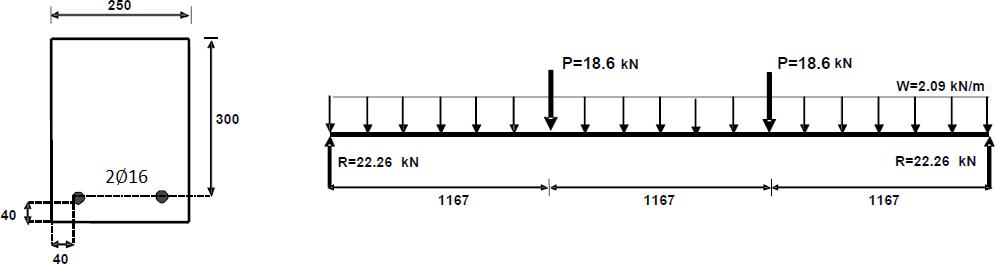
Swobodnie podparta belka teowa o rozpiętości l_{ef}=3×1,2=6 m, o przekroju 300x 450 (d) jest obciążona obliczeniowymi siłami skupionymi P=550 kN (rys. 56), wykonana z C25/30- B500 $ (f_y= 500/1,15=435 \, MPa$)
Rys. 56 Ilustracja do przykładu 3.3.
[zotpressInText item=”{FWPXIWD5,Prz.16.6}”]
Siła poprzeczna na podporze $V_{Ed}=550 \, kN$
Rozważono dwa warianty zbrojenia poprzecznego:
a) tylko strzemiona pionowe,
b) hybrydowe złożone ze strzemion pionowych i prętów odgiętychW przypadku zastosowania zbrojenia hybrydowego nośność prętów odgiętych i nośność strzemion sumuje się, ale strzemiona muszą zapewnić przynajmniej 50% wymaganej nośności.
W wariancie a):
Korzystamy z algorytmu przedstawionego na rys.27
(92) $\to $ $v_{Ed} = \cfrac{550}{300 \cdot 0,9 \cdot 450} \cdot 10^3= 4,53 \, MPa$
Z tab 10 odczytujemy dla betonu C25/30 $\to$ $f_{cd}=17,9 \, MPa$ ; $\nu_1=0,540$ ; $v_{Rd,max}(ctg \Theta=2,5)= 3,33 \, MPa$; $v_{Rd,max} (ctg \Theta=1,0)= 4,82 \, MPa$
Zachodzi $ 3,33 \, < \, v_{Ed}=4,53 \, < \, 4,82 \, MPa \to $ należy wyznaczyć $\Theta$.
Kąt nachylenia krzyżulca betonowego
(111) $\to $ $ \Theta= 0,5 \cdot arcsin (2\cdot 4,53/(0,540\cdot 17,9 )=0,6074 rad= 34,8^o \to ctg \Theta= 1,438 $
W pracy [zotpressInText item=”{FWPXIWD5,Prz.16.6}”] uzyskano $ctg \Theta= 1,432 $
Przyjęto strzemiona Ø 8 czterocięte $A_{sw}=4 \cdot \cfrac{4 \pi[8^2i}{4}=201 \, mm^2$
Wymagany rozstaw dla znanego pola przekroju otrzymamy po przekształceniu zależności (108) w postaci
$$\begin{equation} s \le \cfrac {A_{sw} \cdot f_{yd}} {v_{Ed} \cdot b_w} \cdot ctg \Theta \label {194}\end{equation}$$
czyli $ s \le \cfrac {201 \cdot 435} {4,53 \cdot 300} \cdot 1,438= 93 \, mm $
Ponieważ wymagany rozstaw strzemion jest zbyt mały, więc podjęto decyzję o zastosowaniu zbrojenia hybrydowego , również prętami odgiętymi
Wariant b):
W celu zwiększenia rozstawu między strzemionami, przedział przypodporowy dodatkowo zbrojono prętami odgiętymi. Nośność przekroju jest sumą nośności prętów odgiętych oraz strzemion.
Ze względów konstrukcyjnych zastosowano cztery pręty odgięte Ø 20 pod kątem $\alpha=45^o$ $A_{sw}= 4 \cdot \cfrac{\pi 2^2}{4}=12,57 \, cm^2$
(108) $\to $ nośność prętów odgiętych $ v_{Rd,s} = \cfrac {12,57} \cdot 435 \cdot \sin 45^o \cdot 10^{-1} =386,6 \, kN$
Do przeniesienia przez strzemiona pozostaje $ V_{Ed} = 550-386,6=163,4 \, kN < 0,5 \cdot 550 =275 \, kN \to V_{Ed}=275 \, kN$
Dla takiej siły naprężenia styczne wynoszą: $v_{Ed} = \cfrac{275}{300 \cdot 0,9 \cdot 450} \cdot 10^3= 2,26 \, MPa \, < \, 3,33 \, MPa$ $\to ctg \Theta= 2,5$
Wymagany rozstaw $ s \le \cfrac {201\cdot 435} {2,26 300} \cdot 2,5= 322 \, mm $
Kontrola zarysowania
Zarysowanie przekroju pojedynczo zbrojonego
Dane wg [zotpressInText item=”{ZWDLNK2W,przykład 18.1}”] gdzie obliczenia przeprowadzono metodą KO
Obliczyć szerokość rysy oraz maksymalną średnicę zbrojenia w przekroju prostokątnym
wysokość $h=500 \,mm$, szerokość $b=300 \, mm$, zbrojenie jednostronne $A_{sl} = 12,57 \, cm^2$ (4 Ø 20)
otulenie $c= 40 \,mm$, $a=40+20/2=50 \, mm$, wysokość użyteczna $d_l=500-50=450 \, mm$
beton C 25/30 $\to$ tab.1: $f_{ck}= 25 \, MPa$, $f_{ct,ef}= f_{ctm} = 2,6 \, MPa$, $E_{cm}=31 \, GPa$
stal B490 $\to$ tab. 2: $f_{yd}= 420 \, MPa $ , $ E_s= 200 \, GPa$
(136) $\to $ $\alpha_e=200/31= 6,452$Kombinacja obciążeń quasi-stała: $M_E=124,4 \, kNm$
Przyjęto $E_c = E_{cm}=31 \, GPa$, a nie $E_{c,ef}$, to znaczy rozpatruje się przypadek doraźny, co może być niespójne z obciążeniami quasi-stałymi dla których przyjmowano współczynnik $k_t=0,4 (143) .
użyteczny stopień zbrojenia dolnego $\rho_{sl}=12,57/ (30 \cdot 45)= 0,931 $ %
użyteczny stopień zbrojenia górnego $\rho_{su}=0$ %
użyteczny stopień zbrojenia belki $\rho_{s}=0,931+0 =0,931 $ %
względna wysokość użyteczna $ \delta_l= 450/500=0,9$Kontrola zarysowania
Zarysowanie przekroju pojedyńczo zbrojonego
Obliczenie szerokości rysy metodą KO
I faza pracy
(139) $\to $ wysokość strefy ściskanej
$x_{I} =\cfrac{ 30\cdot 50^2 /2 + 6,452 \cdot ( 0 + 12,57 \cdot 45 ) }{ 30\cdot 50 + 6,452 \cdot (12,57+0) }= 26,025 \, cm$(140) $\to $ moment bezwładności przekroju w I fazie:
$I_I= \cfrac{ 30 \cdot 50^3}{12} + 30 \cdot 50 \cdot (50/2- 26,025)^2 + 6,452 \cdot [ 0 +12,57 \cdot (45 -26,025)^2 ] =343276,6 \, cm^4$odległość włókna skrajnego (betonu) $z_{0,I}= h-x_I= 50 – 26,025= 23,975 \, cm$,
wskaźnik wytrzymałości w I fazie $W_I= \cfrac{ 343276,6}{23.975}=14318,11 \, cm^3$(138) $\to $ moment rysujący $M_{cr}= 14318,11 \cdot 2,6 \cdot 10^{-3}= 37,23 \, kNm$
Moment rysujący przy pominięciu sztywności stali (141) $\to $ $M_{cr}= ( 30\cdot 50^2)/6 \cdot 2,6 \cdot 10^{-3} = 32, 5 /, kNm$. Oszacowanie w przykładzie jest o 37,23/32,5= 15% mniejsze od wartości z uwzględnieniem zbrojenia w sztywności przekroju.
Kryteria zarysowania przekroju:
(137) $\to $ $M_E= 124,4 > M_{cr}= 37,23 \, kNm$,
lub alternatywnie
(126) $\to$ $ \sigma_{cl} = 124,4/ 14318,11 \cdot 10^3= 8,7 > f_{ctm}= 2,6 \, MPa$,
$\to $ przekrój ulegnie zarysowaniu.II faza pracy
Parametry pomocnicze:
(152) $\to$ $\rho_{s,e}= 6,452 \cdot 0,00931$= 0,06007
(153) $\to$ $k_{lu}= (0,931 +0 \cdot 0) / 0,931 =1$Wysokość strefy ściskanej przy założeniu braku betonu rozciąganego
(151) $\to$ $\xi_{II}= \sqrt{ 0,06007 \cdot ( 0,06007 + 2 \cdot 1) } – 0,06007= 0,291709$
$x_{II}= 0,2917109 \cdot 45 = 13,127 \, cm$Naprężenia w zbrojeniu tuż przed pęknięciem
(145) $\to$ Współczynnik efektywnej wysokości $\lambda_{c,ef}=\min { [ 1- 0,291709 \cdot 0,9 )/3 \, ; \, 2,5 \cdot (1-0,9)] } = 0,2458$,
(144) $\to$ Wysokość efektywna betonu rozciąganego $ h_{c,ef}= 0,2458 \cdot 500 = 122,9 \, mm$
Uwaga: W pracy Knauff,… obliczono $h_{c,ef}= 123 \, mm$
(146) $\to$ Stopień zbrojenia strefy rozciąganej: $\rho_{p,ef}=\cfrac {12,57}{ 30 \cdot 12,29}= \cfrac{0,00931\cdot 0,9 }{0,2458} = 0,03409$
(147) $\to$ naprężenia w zbrojeniu tuż przed zarysowaniem : $ \sigma_{s,cr}=0,4 \cdot 2,6 \cdot \left( \cfrac{1}{ 0,03409}+ 6,452 \right )= 37,22 \, MPa$
Uwaga: w pracy Knauff,… $\sigma_{s,cr}$ oznaczono przez $\sigma_0$ i uzyskano wynik 37,7 MPa
Sprawdzenie wartości naprężeń wg formuły (142) $\to$ $\sigma_{s,cr} = 0,4 \cdot 6,452 \cdot 2,6 \cdot (45- 26,026) / (50- 26,026) = 5,31 \, MPa $
Naprężenia z formuły eksperymentalnej (147) są znacznie większe od naprężeń teoretycznych (142).(155) $\to$ moment bezwładności przekroju w II fazie: $ I_{II}= 30 \cdot 13,127^3 / 3 + 6,452 \cdot 12,57 \cdot (45-13,127 )^2 + 0= 105010 /, cm^4$
(156) $\to$ naprężenia w pręcie zbrojeniowym po zarysowaniu przekroju:
$\sigma_s = 6,452 \cdot 124,4 / 105010 \cdot (45 – 13,127) \cdot 10^3 = 243,6 MPa$
Uwaga: w pracy Knauff,… metodą uproszczoną uzyskano $\sigma_s= 258,7 MPa$, czyli o 6% więcej.
Przyrost naprężeń w zbrojeniu
(165) $\to$ $\Delta \sigma= \max{\{ 243,6 – 37,2 \, ; \, 0,6 \cdot 243,6 \} }= 206, 4 \, MPa$
Odkształcenie pękania
(166) $\to$ Odkształcenie pękania : $ \varepsilon_{cr}=\cfrac{206,4}{200\cdot 10^3}=1,032 \cdot 10^{-3}$
Rozstaw rys
Dla danych: pręt $ \Phi=20 \, mm$, otulenie $c=40 \, mm$, $k_1=0,8$ – pręty żebrowane, $k_2=0,5$ – zginanie, $k_3$=3,4 , $k_4$= 0,425:
(156) $\to$ Rozstaw rys: $ s_{r,max}= 3,4 \cdot 40 +0,8 \cdot 0,5 \cdot 0,425 \cdot \cfrac{20}{0,0341} = 235,7 \, mm$
Uwaga: w pracy Knauff,… uzyskano wynik 237,4 mm
Rozwarcie rys
(157) $\to$ $w_k = 206,4 \cdot 1,032 \cdot 10^{-3} = 0,243 \, mm$ <$w_{max} ( \ref{134} \to)= 0,3 \, mm$
Uwaga: w pracy Knauff,… uzyskano wynik 0,262 mm
Obliczenie szerokości rysy metodą UO
Powyżej obliczono:
rozstaw rys $ s_{r,max} = 235,7 \, mm$
moment rysujący $M_{cr} =32,91 \, kNm$
naprężenie w stali $\sigma_s = 243,62 MPa$pod (164) $\to$ $\beta = 1/2 $ dla obciążeń prawie stałych
(169) $\to$ $w_k= 235,7 \cdot \left[ 1 – 1/2 \cdot \left( \cfrac{32,91}{124,4} \right)^2\right ] \cdot \cfrac {243,62}{200} \cdot 10^{-3} =0,232\, mm $
Metodą UO uzyskano szerokość rysy o 0,243/0,232=5% więcej. Taka różnica wystąpiła przy obliczeniach dwoma metodami według jednej normy . Większe różnice, ponad dwukrotne, występują pomiędzy różnymi normami narodowymi (np. [zotpressInText item=”{59RBVIR8}”], [zotpressInText item=”{MJSQEBRG}”]).
Obliczenie szerokości rysy kalkulatorem KŻ
W kalkulatorze zbrojenia zaimplementowano opisane procedury szacowania szerokości rys. Na rys. 57 pokazano ekran kalkulatora zarysowania z wynikami uzyskanymi dla danych z przykładu 6.1.
Rys. 57 Ekran Rysy do przykładu 6.1
(kliknij na obraz, aby pobrać)
Metodą KO otrzymano $w_k= 0,343 \, mm$, a metodą UO $w_k= 0,232 \, mm$. Rożnica jest nieistotna , biorąc pod uwagę poziom dokładności metod (p. Przykład 6.3)
Zarysowanie przekroju podwójnie zbrojonego
[zotpressInText item=”{M5CRS5B7,Example 7.3, 7.4}”]
Dane ogólne
Przekrój prostokątny podwójnie zbrojony: $b = 400 \, mm, h = 600 \,mm$ , zbrojony dołem $A_{sl} = \, 2714 mm^2 \, (6 Ø 24)$, górą $ A_{su} =452 \, mm^2 \, (4 Ø 12)$ z otuleniem $c=40 \, mm$,
wykonany z betonu C30/37, (tab 1) $\to$ $f_{ck}=30 \,MPa$, $fct_{eff}=f_{ctm}=2.9\, MPa$, $E_{cm} = 33 \, GPa$ ,
czyli: $a_l = 40+24/2 = 52 \, mm$, $a_u= 40+12/2 = 46 \, mm$ , $d_l = 600- 52= 548 \, mm$,Przyjąć krótkotrwałe działanie obciążenia (143) $\to$ $k_t=0,6$
Pominąć sprawdzenia w fazie I, ograniczając się do wyliczenia szerokości rysy oraz maksymalnej średnicy zbrojenia ze względu na zarysowanie.
Moduł sprężystości betonu w szczególnych warunkach pełzania
Wysokość zastępcza belki do oszacowania współczynnika pełzania $h_0= (h\cdot b/(2\cdot h +b)= 400\cdot 600/(2*600+400)= 150 \, mm$
Ponieważ belka będzie eksploatowana w szczególnych warunkach pełzania: w środowisku o wilgotności RH=88,3% i przez 5 lat, więc końcowy współczynnik pełzania należy obliczyć z ogólnych zależności. Zastosowano kalkulator CH-P, którego ekran pokazano na rys. 58. wyniku otrzymano :
$\varphi(5 lat, 28 dni) =1,476$., czyli:(126) $\to$ E_{c,ef} = 33/(1+1,476)= 13,33 \, GPa$
(136) $\to$ $\alpha_e= \alpha_{e,ef} = 200/13,33= 15 $
Rys.58. Ekran kalkulatora pełzania do przykładu 6.2.
(kliknij na obraz, aby pobrać)
Uwaga:
W warunkach normalnych określonych w tab.11 : współczynnik pełzania końcowego dla C30/37, $t_0=28 \, dni$ $ h_0=120 \, mm$ $\to$ $ \varphi( \infty, 28)=2,545$
(126) $\to$ $E_{c,ef} = 33/(1+2,545)= 9,31 \, GPa$ , $\alpha_e= 200/9,31= 21,5 $Parametry pomocnicze:
$\rho_{sl}= 2714/(400\cdot 548)=0,01238$,
$\rho_{su}= 452/(400\cdot 548)=0,00206$,
$\rho_s=0,01238+0,00206 =0,01444$,
$\delta_l= 548/600= 0,9133$
$\delta_{u/l}= 46/548= 0,08394$
(152) $\to$ $\rho_{s,e}= 15 \cdot 0,01444$= 0,2168
(153) $\to$ $k_{lu}= (0,01238 +0,00206 \cdot 0,08394) /0,01444 =0,87$Wysokość strefy ściskanej w II fazie
(151) $\to$ $\xi_{II}= \sqrt{ 0,2168\cdot (0,2168 + 2 \cdot 0,87) } – 0,2168= 0,4344$
$x_{II}= 0,4344 \cdot 548 = 238 \, mm$Uwaga: W pracy [zotpressInText item=”{M5CRS5B7,Example 7.3, 7.4}”] uzyskano $x_{II}=237,8 \, mm$ , odnosząc stopień zbrojenia przekroju do wysokości przekroju $h$, a nie do wysokości użytecznej $d_l$
Naprężenie w zbrojeniu przed zarysowaniem
($\ref{145}$) $\to$ Współczynnik efektywnej wysokości $\lambda_{c,ef}=\min { [1- 0,4344 \cdot 0,9133 )/3 \, ; \, 2,5 \cdot (1-0,9133)] }= 0,2411$,
($\ref{144}$) $\to$ Wysokość efektywna betonu rozciąganego: $ h_{c,ef}= 0,201 \cdot 600 = 120,6 \, mm$
($\ref{146}$) $\to$ Stopień zbrojenia strefy rozciąganej: $\rho_{p,ef}=\cfrac {27,14}{ 40 \cdot 12,06}= \cfrac{0,01238 \cdot 0,913 } {0,2011} = 0,0562$($\ref{147}$) $\to$ naprężenia w zbrojeniu tuż przed zarysowaniem : $ \sigma_{s,cr}=0,6 \cdot 2,9 \cdot \left( \cfrac{1}{ 0,0562}+ 15 \right )= 57,1 \, MPa$
Moment bezwładności w fazie II i naprężenie w zbrojeniu po zarysowaniu
$(\ref{155}) \to$ $ I_{II}= \cfrac { 40 \cdot 23,8^3}{3 } + 15 \cdot \left [ 27,14 \cdot (54,8 -23,8 )^2+ 4,52 \cdot (13,58-4,6)^2 \right ]=595967 \, cm^4$
($\ref{156}$) $\to$ naprężenia w pręcie zbrojeniowym po zarysowaniu przekroju:
$\sigma_s = 15 \cdot 300 / 595967 \cdot (54,8 – 23,8) \cdot 10^3 = 234,1 MPa$Zarysowanie przekroju
przyrost naprężeń w stali ($\ref{165}$) $\to$ $\Delta \sigma= \max{\{ 234,1 – 57,1 \, ; \, 0,6 \cdot 234,1 \} }=177 \, MPa$
odkształcenie pękania ($\ref{166}$) $\to$ : $ \varepsilon_{cr}=\cfrac{177 }{200\cdot 10^3}=0,885 \cdot 10^{-3}$,
rozstaw rys ($\ref{156}$) $\to$ $ s_{r,max}= 3,4 \cdot 40 +0,8 \cdot 0,5 \cdot 0,425 \cdot \cfrac{24}{0,0562} = 208,6 \, mm$,
rozwarcie rys ($\ref{157}$) $\to$ $w_k = 208,6 \cdot 0,885 \cdot 10^{-3} = 0,185 \, mm$ <$w_{max} \ref{134} = 0,3 \, mm$..Szerokość rozwarcia rysy z kalkulatora CH-P Ż
Rys. 59 Ekran Rysy do przykładu 6.2.
(kliknij na obraz, aby pobrać)
Kontrola zarysowania w normach europejskiej, australijskiej i amerykańskiej
W przykładzie przedstawiono metodę obliczania szerokości pęknięć i odstępów między pęknięciami stosowane w normach krajowych: EC2, MC- 90 oraz ACI318-99. i porównano z wynikami badań eksperymentalnych przedstawionych w [zotpressInText item=”{59RBVIR8}”] na przykładzie belki, pokazanej na rys. 60.
Rys. 60 Belka B1-a z pracy Nejadi (2005)
Obliczenia zostały przeprowadzone dla rzeczywistych parametrów belki zmierzonych w pracy [zotpressInText item=”{59RBVIR8}”], a mianowicie:
$h=348 \, mm$ , $b=250 \, mm$ $c=40 \, mm$, $\Phi= 16 \, mm$ ,
$a_l= 40+16/2= 48 \, mm$, $d_l=300 \, mm$, $A_{sl}= 400 \, mm^2$,
$E_c$=22,82 \, GPa$ , $f_{ct}=2.8 \, MPa$ , $Es=200 \, GPa$ ,
$M_{max}=24.91 \, kNm$ ,
W przykładzie nie posługiwano się symbolem betonu ani staliParametry ogólne (niezależne od norm)
($\ref{136}$) $\to \alpha_e=200/22,82= 8,76$
$\rho_{su}=0$,
$\rho_{sl}=(400/(250 \cdot 300)= 0,00533$,
$\rho_=0+0,00533 =0,0,00533$,
$\delta_l= 300/348= 0,862$
$\delta_{u/l}= 0/548= 0$($\ref{152}$) $\to$ $\rho_{s,e}= 8,76 \cdot 0,00533$= 0,0467
($\ref{153}$) $\to$ $k_{lu}= (0,00533 +0) /0,00533 =1$($\ref{151}$) $\to$ $\xi_{II}= \sqrt{0,0467\cdot (0,0467 + 2 \cdot 1) } – 0,0467= 0,263$,
$x_{II}=0,263 \cdot 300=78,8 \, mm$
$(\ref{155}) \to$ $ I_{II}= \cfrac { 25 \cdot 7,88^3}{3 } + 8,76 \cdot 40 \cdot (30 -7,88 )^2 = 2122,24 \, cm^4$
Obliczenia wg EC2
($\ref{145}$) $\to$ Współczynnik efektywnej wysokości
$\lambda_{c,ef}= \min { [ {1- 0,263 \cdot 0,862 )/3 \, ; \, 2,5 \cdot (1-0,862)] }= 0,2578$ ,
($\ref{144}$) $\to$ Wysokość efektywna betonu rozciąganego: $ h_{c,ef}= 0,201 \cdot 600 = 120,6 \, mm$,
($\ref{146}$) $\to$ Stopień zbrojenia strefy rozciąganej: $\rho_{p,ef}=\cfrac {27,14}{ 40 \cdot 12,06}= \cfrac{0,01238 \cdot 0,913 }{0,2011} = 0,0562$,
($\ref{147}$) $\to$ naprężenia w zbrojeniu tuż przed zarysowaniem : $ \sigma_{s,cr}=0,6 \cdot 2,9 \cdot \left( \cfrac{1}{ 0,0562}+ 15 \right )= 57,1 \, MPa$
W trakcie sporządzania
Ugięcia belek w stanie zarysowanym
Linia ugięcia belki obciążonej odcinkowo
Obliczyć ugięcie belki przedstawione na rys. 61 po następujących okresach (rys.31):
- okresie I – okresie pielęgnacji betonu $ [ 0, t_s] $, gdzie $t_s= 14 \, dni$
- okresie II – okresie budowy $ [ 0, t_m] $, gdzie $t_m= 14 \, dni$
- okresie III – okresie przygotowania do oddania do użytkowania $[t_m \,; t_0]$,, gdzie $t_0= 60 dni$
- okresie eksploatacji $[t_0, \infty]$ , gdzie $\infty = 50 lat$
Charakterystyki przekroju belki
Belka prostokątna ma przekrój 300×200 mm i pozostałe dane zgodnie z rys. 61 i 62.
Rys.62 Ekran wstępny kalkulatora CH-P Ż do przykładu 7.1
Arkusz z danymi przykładu można pobrać przez kliknięcie na obraz rys.60.
W zakładce „Rysy” można sprawdzić dane przy których wyznaczono rozwarcie rys. W zakładce „Pełzanie” podano parametry i wyniki przyjęte do obliczenia współczynnika pełzania. W zakładce „Robol” zestawiono wszystkie dane i pośrednie wyniki w , w tym sztywności przekroju w fazie I i II.Charakterystyki przekroju na koniec okresów życia ( z uwzględnieniem pełzania)
Z zakładki „Pełzanie” arkusza pobranego pod rys. 60 odczytujemy:
końcowy współczynnik pełzania $\varphi(\infty, 28 dni)= 2,759$
skurcz betonu (po 28 dniach) $\epsilon_{cs}= 0,550$ ‰.(tab.1) dla C30/37
$E_{cm}= 33 \, GPa$
$f_{ctm} = 2,9 \, MPa $
($\ref{126}$) $\to$ $E_{c,ef}= 33 / (1+2,759)= 8, 78 \, GPa$
$(\ref{136}) \to $ $\alpha_e=200/ 8,78=22,78$,$A_{sl}=A_{su}= 8,04 /, cm^2$
$a_u=a_l=40+16/2= 48 \, mm$
$d_l=300-48 =252 \,mm$Wysokość strefy ściskanej i moment bezwładności w fazie I
$(\ref{139}) \to$ $ x_I =\cfrac{ 20\cdot 30^2 /2 + 22,78 \cdot ( 8,04 \cdot 25,2 ) + 8,04 \cdot 4,8 } { 20 \cdot 30 + 22,78 \cdot ( 8,04 + 8,04) } =15,0 \, cm$
$(\ref{140} \to $) I_I= \cfrac{20 \cdot 30^3}{12} +20 \cdot 30 \cdot (30/2 -15 )^2 + 22,78 \cdot 8,04 \cdot (25,2 -15 )^2 +8,04 \cdot (15-4,8)^2) ]= 64059 \, cm^4$(\ref{178} \to $ S_F= 8,04 \cdot ( 25,2 -15 ) -8,04 \cdot (15 – 4,8) = 0,00 \, cm^3 $
Moment rysujący
odległość włókna dolnego od osi obojętnej przekroju. w fazie I : $ z_0=30 -15= `5 \, cm $
wskaźnik wytrzymałości przekroju przed zarysowaniem: $W_{cr} = I_{cr} / z_0 = 64059/15= 4270,5 \, cm^3$ ;$(\ref{138} \to $) $ M_{cr}= f_{ctm} \cdot W_{cr} =2,9 \cdot 4270,5 \cdot 10{-3}= 12, 38 \, kNm$
Wysokość strefy ściskanej i moment bezwładności w fazie II
$\rho_{su}= \rho_{sl} = 8,04/(20* 25,2) = 0,01592$
$\rho_s=0,01592+0,01592 = 0,03191$
$delta_{u/l}= 48/252=0,190$
$(\ref{153}) \to$ $k_{lu}= (0,01592 +0,190 \cdot 0,01592) / 0,0319 = 0,5952$,
$(\ref{152}) \to$ $\rho_{s,e}= 22, 78 \cdot 0,03191 = 0,7269$
$(\ref{151}) \to$ $ \xi_{II}= \sqrt{ 0,7269 \cdot ( 0,7269 + 2 \cdot 0,5952) } \, – 0,7269 =0,45367 $$x_{II}=,45367 \cdot 25,2 =11,43 \,cm $
$(\ref{178} \to $ S_F= 8,04 \cdot ( 25,2 -11,43 ) -8,04 \cdot (11,43 – 4,8) = 57,37 \, cm^3 $
Momenty równoważne od skurczu betonu
$(\ref{177}) \to$
$ M_{cs,I} = 200 \cdot 0,0 \cdot 0,55 =0 $,
$ M_{cs,I} = 200 \cdot 57,37 \cdot 0,55 \cdot 10^{-3}=6,31 \,kNm $,Obciążenia charakterystyczne oraz indeksy SGU1/SGN, SGU2/SGN
W tab. 13 zestawiono współczynniki redukcyjne w obliczeniowej oraz charakterystycznych kombinacjach obciążeń.
Na długości 3 m (wg rys. 59) na belkę działają obciążenia z pasa stropodachu o szerokości a= 3 m pochodzące od następujących obciążeń prostych:
G= 6 , kN/m^2 \cdot 3 \, m= 18 \, kN/m$ – obciążenie stałe (od ciężaru własnego oraz ciężaru warstw posadzki),
Q_u= 2,5 , kN/m^2 \cdot 3 \, m= 7,5 \, kN/m$ – obciążenie zmienne (obciążenia użytkowe),
S= 1 , kN/m^2 \cdot 3 \, m= 3 \, kN/m$ – obciążenie zmienne od śniegu,
W= – 0,6 kN/m^2 \cdot 3 \, m= -1,8 \, kN/m$ – obciążenie zmienne od wiatru (ssanie) -pomijane jako korzystne.
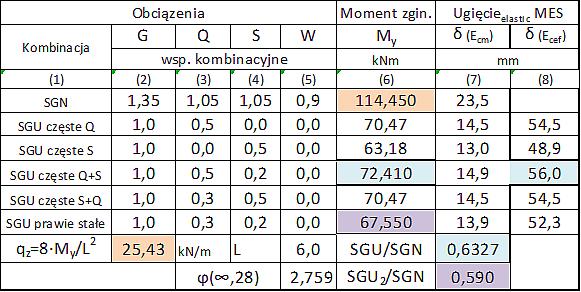
Tab.13 . Wyznaczenie indeksów obciążeń do przykładu 7.1
W kol(1) podano nazwę kombinacji, a w kol (2) do (5) iloczyn współczynnika obciążeń i redukcyjnego $\gamma_F \cdot (\psi_0 \, , \, \psi_1 l\, lub \, \psi_2) $ odpowiedni do sytuacji obliczeniowej. Ponieważ w sytuacji charakterystycznej $\gamma_F=1$, więc podane wartości są współczynnikom redukcyjnym (wartości częstej lub prawie stałej). W kol (6) podano sprawczy (maksymalny) moment zginający $M_y$ w danej kombinacji obciążeń uzyskany z obliczeń statycznych MES dla stałej sztywności belki pod długości. Wynikają stąd następujące indeksy SGU/SGN:
($\ref{132}$) $\to$ SGU1/SGN $=\cfrac{72,41} {114,45}=0,6327 $
($\ref{133}$) $\to$ SGU2/SGN $=\cfrac{67,55}{114,45} =0,590$
W kol (1) w wierszu $q_z$ podano równomiernie rozłożone na całej długości belki, obliczeniowe obciążenie zastępcze belki powodujące taki sam moment sprawczy jak obciążenie rzeczywiste.
$q_z= \cfrac{8 \cdot 114, 45}{6,0^2} = 25.43 \, kN/m$
Dodatkowo w kol. (7) i (8) podano ugięcia belki uzyskane metodą MES dla belki sprężystej (niespękanej) w dwóch sytuacjach: doraźnej ( dla modułu $E_{cm}$ ) oraz końcowej (dla modułu efektywnego $E_{c,ef}=E_{cm} / (1+ \varphi( \infty \, , 28
________________________________
