Niniejszy artykuł jest Dodatkiem C podręcznika Imperfekcyjna metoda projektowania konstrukcji
Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda projektowania konstrukcji, Encyklopedia πWiki,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]
Historia edycji:
(2019-05-02) Dodatek C : Neiliniowy geometrycznie pręt o przekroju zwartym Wersja 1.0 (2019-05-02)
Proszę społeczność Inżynierów w internecie o przesyłanie recenzji podręcznika na adres wydawnictwa biuro@chodor-projekt.net
Leszek Chodor
Przedstawiono geometrycznie nieliniową metodę elementów skończonych prostych prętów o przekroju zwartym, użyteczną przy analizie wpływu rzędu nieliniowego na efekt P-Delta
Pręt nieliniowy geometrycznie
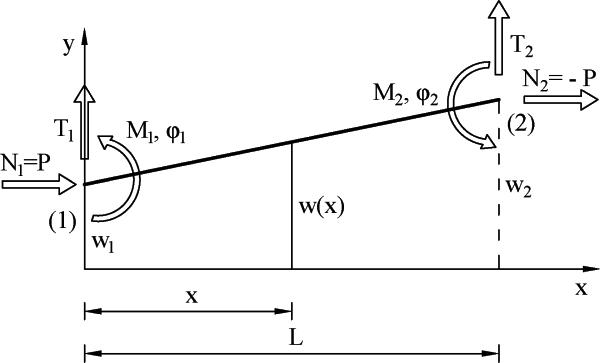
Wyznaczymy ścisłą, nieliniową macierz sztywności oraz strzałkę ugięcia elementu prętowego przekroju zwartym, ściskanego siłą osiową P. Element [e] z węzłami (1)-(2) pokazano na Rys. C.1.
Ścisła macierz sztywności
Nieliniową macierz sztywności ściskanego elementu prętowego wyznaczymy w drodze rozwiązania równania różniczkowego ($\ref{C.1}$) belki-słupa bez obciążenia poprzecznego:
$$\begin{equation} EI w^{iv} +Pw^{i} =0 \label {C.1} \end {equation} $$
Wprowadzamy zmienną $\xi=\cfrac{x}{L}$ oraz miarę obciążenia $\lambda^2=\cfrac{PL^2}{EI}=\pi^2 \alpha_{cr} \to \lambda=\pi \sqrt{\alpha_{cr}}$ , gdzie $\alpha_{cr}= \cfrac{P}{P_{cr}}$ (1.9) dla obciążenia krytycznego Eulera $P_{cr}=\pi^2 EI/L^2$. W granicznym stanie krytycznym $\alpha_{cr}=1$ i stopień wytężenia siła ściskającą $\lambda=\pi$.
Równanie pręta ($\ref{C.1}$) można teraz przepisać do postaci
$$\begin{equation} \cfrac{d^4 w}{d \xi^2}+ \lambda^2 \cfrac{d^2 w}{d \xi^2}=0 \label {C.2} \end {equation} $$
Rozwiązanie równania ($\ref{C.2}$) można zapisać w postaci:
$$\begin{equation} w(\xi) = C_1 +C_2 \lambda \xi +C_3 \cos{( \lambda \xi)} + C_4 \sin{( \lambda \xi)} \label {C.3} \end {equation} $$
Po wykonaniu różniczkowania funkcji ugięcia uzyskamy funkcję obrotów
$$ \begin{equation} \cfrac{ d w ( \xi )} { d \xi } = \lambda [ C_2 + C_3 \sin{ ( \lambda \xi) } + C_4 \cos { ( \lambda \xi )} ] \label {C.3a} \end {equation} $$
Warunki brzegowe wynoszą:
$$\begin{equation} w(0)= w_1 , \quad w (1)=w_2, \quad \cfrac{d w(0)}{d \xi} = \varphi_1 L, \quad \cfrac{d w(1)}{d \xi} = \varphi_2 L \label {C.4} \end {equation} $$
Warunki brzegowe ($\ref{C.4}$) można zapisać w formie macierzowej:
$$\begin{equation} [D] \cdot \left [ \begin {array}{c} C_1 \\ C_2 \\ C_3 \\ C_4 \end {array} \right ] = \left [ \begin {array}{c} w_1 \\ \varphi_1 L \\ w_2 \\ \varphi_2 L \end {array} \right] , \text {gdzie } [D]=
\left [ \begin {array} {ccc} 1 & 0 &1 &0 \\ 0 & \lambda & 0 & \lambda \\ 1 & \lambda & \cos {\lambda} & {\sin \lambda} \\ 0 & \lambda & -\lambda \sin{ \lambda} & \lambda \cos{ \lambda} \end {array} \right ] \label {C.5} \end {equation} $$
Po odwróceniu macierzy [D] , otrzymamy:
$$\begin{equation} [D]^{-1} =\cfrac{1}{\Theta} \left [ \begin {array}{cccc}
\lambda \beta & \gamma & \lambda (1- \cos{ \lambda}) & – ( \lambda – \sin{ \lambda} ) \\
\lambda \sin{ \lambda} & 1- \cos{\lambda} & -\lambda \sin{\lambda} & 1- \cos { \lambda} \\
\lambda (1- \cos{ \lambda}) & -\gamma & -\lambda(1-\cos{ \lambda}) & \lambda -\sin {\lambda} \\
– \lambda \sin{\lambda} & \beta & \lambda \sin { \lambda} & -(1-\cos{ \lambda})\\
\end {array} \right] \label {C.6} \end {equation} $$
gdzie:
$\Theta=2 \lambda (1-\cos {\lambda})- \lambda^2 \sin{\lambda}$,
$ \beta= 1- \cos{\lambda } -\sin{\lambda }$,
$\gamma=\lambda\cos{\lambda }-\sin{\lambda }$.
Stałe całkowania wynoszą
$$\begin{equation} \left [ \begin {array} {c} C_1 \\ C_2 \\ C_3 \\ C_4 \end {array} \right ] = [D]^{-1}
\left [ \begin {array}{c} w_1 \\ \varphi_1 L \\ w_2 \\ \varphi_2 L \end {array} \right ] =
\cfrac{1}{\Theta} \left [ \begin {array} {c}
\lambda (\Sigma w -\varphi_2 L)+ \lambda(\varphi_1 L -\Sigma w ) \cos{\lambda}- (\lambda^2 w_1 -\Delta \varphi L) \sin{\lambda} \\
\Sigma \varphi L \cdot (1-\cos{\lambda}) -\lambda \Delta w \sin {\lambda} \\
\lambda(\varphi_2L -\Delta w ) -\lambda(\varphi_1 L -\Delta w) \cos{\lambda} -\Delta \varphi L \sin {\lambda} \\
-\Delta \varphi L \cdot (1-\cos{\lambda}) -\lambda (\varphi_1 L -\Delta w ) \sin {\lambda} \\
\end {array} \right ] \label {C.7} \end {equation} $$
Siły przekrojowe uzyskamy z zależności:
$$\begin{equation} M=EI w^{ii} = – \cfrac{EI}{L^2} \cfrac{dw^2}{d\xi}= \lambda^2 \cfrac{EI}{L^2} (C_3 \cos{\lambda \xi} +C_4 \sin{\lambda \xi}) \label {C.8} \end {equation} $$
$$\begin{equation} T=M^{i} = – \cfrac{EI}{L^3} \cfrac{dw^3}{d \xi} = \lambda^3 \cfrac{EI}{L^3} ( – C_3 \sin{\lambda \xi} +C_4 \cos{\lambda \xi}) \label {C.9} \end {equation} $$
Wektor sił węzłowych wynosi
$$\begin{equation} \left [ \begin {array} {c} M_1 \\ T_1 \\ M_2 \\ T_2 \end {array} \right ] =
\left [ \begin {array} {c} M(\xi=0) \\ T(0) \\ M(1)\\ T(1) \end {array} \right ] =
\lambda^2 \cfrac{EI}{L^2} \cdot \left [ \begin {array} {cc} 1 & 0 \\ 0 & \cfrac{\lambda}{L} \\ \cos{\lambda} & \sin {\lambda} \\ \cfrac {- \lambda}{ L \sin{\lambda}} & \cfrac{ \lambda}{ L \cos{\lambda}}
\end {array} \right ]
\cdot \left [ \begin {array} {c} C_3\\ C_4 \end {array} \right ]
\label {C.10} \end {equation} $$
Po przekształceniach powyższych wyrażeń (pokazano w pracy [1]), uzyskamy macierz sztywności nieliniowego geometrycznie pręta ściskanego w postaci:
$$\begin{equation} [k]^{[e]} = \left [ \begin {array} {cccccc}
\cfrac{EA}{L} & 0& 0 & \cfrac{-EA}{L} &0 &0 \\
& \cfrac{12 EI}{L^3} \Lambda_1 & \cfrac{6EI}{L^2} \Lambda_2 & 0 & \cfrac{-12 EI}{L^3} \Lambda_1 & \cfrac{6EI}{L^2} \Lambda_2 \\
& & \cfrac{4EI}{L} \Lambda_3 & 0 & \cfrac{-6EI}{L^2} \Lambda _2& \cfrac{2EI}{L} \Lambda_4 \\
& & & \cfrac{EA}{L} & 0 & 0 & \\
& SYM & & & \cfrac{12EI}{L^3} \Lambda_1 & \cfrac{-6 EI}{L^2} \Lambda_2 \\
& & & & & \cfrac{4 EI}{L} \Lambda_3 \\
\end {array} \right ] \label {C.11} \end {equation} $$
Macierz ($\ref{C.11}$) zawiera konwencjonalne współczynniki pręta zginanego zmodyfikowane współczynnikami $\Lambda_i \quad (i=1,..,4)$ [2], [1].
Współczynniki $\Lambda_1$ do $\Lambda_4$ definiują ścisłą geometrycznie nieliniową macierz sztywności pręta ściskanego, zależą od wielkości siły osiowej N w elemencie, wywołanej siłami P na konstrukcji na Rys. C.1) i wynoszą:
$$\begin{equation} \begin {cases}
\Lambda_1= & \alpha_c \cdot \Lambda_2 \\
\Lambda_2= & \cfrac{\alpha^2}{3(1-\alpha_c) } \\
\Lambda_3= & \cfrac{3}{4} \Lambda_2+\cfrac {\alpha_c}{4} \\
\Lambda_4= & \cfrac{3}{2} \Lambda_2 -\cfrac{\alpha_c}{2} \\
\end{cases} \label {C.12} \end {equation} $$
gdzie $\alpha_c=\alpha \cdot ctg{\alpha}$,
Współczynnik $\alpha$ wynosi
$$\begin{equation} \alpha= \cfrac{\lambda}{2}= \cfrac{\pi}{2} \sqrt{\cfrac{N}{N_{cr}}} \label {C.13} \end {equation} $$
W przypadku znajomości siły osiowej w elemencie, współczynniki ($\ref{C.12}$), pozwalają wyznaczyć ścisłą sztywność elementu i w rezultacie nieliniową sztywność systemu konstrukcyjnego. W prostych przypadkach metoda jest użyteczna do obliczeń symbolicznych oraz porównawczych.
W przypadku konwencjonalnych obliczeń MES , polegających na rozwiązywaniu liniowego układu równań współczynniki $\Lambda_i$ wywołują nieliniowość i potrzebę iteracyjnego rozwiązywania systemu konstrukcyjnego. Do tego celu użyteczne jest rozwinięcie funkcji $\Lambda_i \quad (i=1,2,3,4)$ w szereg Taylora podług potęg $\cfrac{NL^2}{EI}$:
$$\begin{equation} \Lambda_i \approx \sum \limits_{i=0}^{i=4} C_{1,i} \cdot \left( \cfrac{NL^2}{EI} \right)^i \label {C.14} \end {equation} $$
Współczynniki rozwinięcia zestawiono w Tab. C.1. Rozwinięcie ścisłej macierzy sztywności w szereg potęgowy podług potęg , jest stosowane w klasycznej analizie mechaniki. Człony liniowe są zachowywane w klasycznej, liniowej analizie wyboczenia (LBA), a mnożniki w kolumnie (1) Tab. B.1. określają tak zwaną macierz geometryczną. W teorii 2 rzędu (efekt P-Δ) są zachowywane człony wyższych rzedów $(\cfrac{NL^2}{EI})^2 $, itd.
Tab. C.1. Współczynniki $C_{1,i}$ rozwinięcia funkcji w szereg Taylora podług potęg $\cfrac{NL^2}{EI}$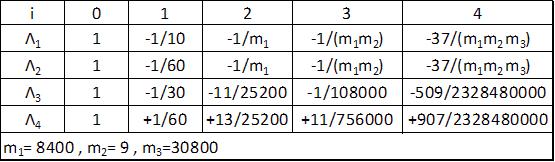
W analizach wpływu stopnia nieliniowości teorii na efekty, bardziej użyteczne jest rozwinięcie funkcji szereg podług potęg współczynnika ($\ref{C.10}$) :
$$\begin{equation} \Lambda_i \approx \sum \limits_{i=0}^{i=4} C_{2,i} \cdot \alpha^i \label {C.15} \end {equation} $$
Tab. C.2. Współczynniki $C_{2,i}$ rozwinięcia funkcji w szereg Taylora podług potęg $\alpha$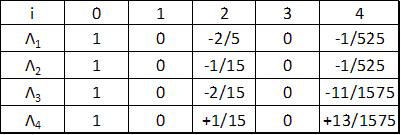
Strzałka ugięcia prostego pręta ściskanego
Z zależności ($\ref{C.2}$) po podstawieniu uzyskanych wyrażeń na stałe całkowania można wyznaczyć funkcję ugięcia pręta pomiędzy węzłami w zależności od przemieszczeń węzłowych:
$$\begin{equation} w(\xi)=\cfrac{1}{\Theta}
\left [ \begin {array} {c}
1- \cos{\lambda} +\cos{ \lambda \xi} -\cos{[ \lambda(1-\xi)] } – \lambda \sin { [\lambda(1-\xi)] } \\
– \lambda \xi – \lambda (1-\xi) \cos{\lambda}+\xi\cos{ [ \lambda(1-\xi)] } +\sin{\lambda} +\sin{[ \lambda\xi] } \sin{[ \lambda(1-\xi)] } \\
1- \cos{\lambda} -\cos{\lambda \xi} +\cos{[ \lambda(1-\xi)] } -\lambda \xi \sin \lambda \\
– \lambda (1- \xi ) – \lambda \xi \cos{\lambda} +\lambda \cos{\lambda \xi } +\sin{\lambda} – \sin{\lambda \xi } -\sin { [\lambda(1-\xi ) ]} \\
\end {array} \right ]
\cdot \left [ \begin {array} {cc} \lambda w_1 & \varphi_1 L & \lambda w_2 & \varphi_2 L\end {array} \right ]
\label {C.16} \end {equation} $$
Z formuły ($\ref{C.16}$) wynika, że pręt idealnie prosty, ugina się pod wpływem osiowej siły ściskającej w każdym przypadku, gdy węzły doznają przemieszczeń liniowych lub obrotów wstępnych, czyli w każdej konstrukcji rzeczywistej.
W stanie granicznym krytycznym, dla $\lambda= \pi$ mamy:
$$\begin{equation} w(\xi)=\cfrac{1}{2 \pi} \left [ \Sigma w +\Sigma \varphi L (\xi-1/2) + \cfrac{ \pi}{2} [ \Sigma \varphi L -2 \Delta w ] \cos{ ( \pi \xi)}- \Delta \varphi L sin (\pi \xi) \right ] \label {C.17} \end {equation} $$
Maksymalne ugięcie pręta, czyli strzałka wygięcia wystąpi w miejscu pręta o współrzędnej $\xi_{sup}$
$$\begin{equation} \xi_{sup} = \pm \cfrac{1}{\lambda} \cdot arcos {(\pm \Gamma)} \label {C.18} \end {equation} $$
gdzie $ \Gamma = \cfrac {1} { \sqrt{ (C_3/C_4)^2 +1}} $. Wyrażenie uzyskano w drodze porównania do zera drugiej pochodnej funkcji $\ref{C.3}$), a w rezultacie uzyskano cztery pierwiastki (przy wszystkich kombinacjach znaków).
Po odrzuceniu pierwiastków ujemnych jako fizycznie niemożliwych i po podstawieniu dodatniej współrzędnej ($\ref{C.18}$) do ($\ref{C.16}$) otrzymamy strzałkę ugięcia pręta w zalezności od warunków brzegowych wyrażonych stałymi $C_3 , C_4$.
W przypadku symetrycznych warunków brzegowych strzałka ugięcia wystąpi w środku pręta i wyniesie
$$\begin{equation} f=w (\xi =0,5 ) = \cfrac{1}{2} \left ( \Sigma w -\cfrac { tg(\lambda/4) \cdot \Delta \varphi L }{\lambda}\ \right) \label {C.19} \end {equation} $$
W granicznym stanie krytycznym: $ \lambda=\pi$ i strzałka ugięcia $(\ref{C.19}$) osiągnie wartość:
$$\begin{equation} f_{cr} = \cfrac{\Sigma w}{2} – \cfrac{\Delta \varphi L}{2 \pi} \label {C.20} \end {equation} $$
Dla $N=0$ jest $\lambda=0$, więc $f_0 = \lim \limits_{\lambda \to 0}= (\Sigma w) /2 -(\Delta \varphi L) / 8 $, co jest zgodne z rezultatem teorii I rzędu.
Wyrażenia $(\ref{C.17})$ i $(\ref{C.20})$ są fundamentalnymi wynikami niniejszego rozdziału. Wskazują ono, że w granicznym stanie krytycznym (Eulera):
- Funkcja ugięcia m postać $(\ref{C.17})$, to znaczy jest mieszaną funkcją liniową z sinusoidą oraz kosinusoidą, można więc ją sprowadzić do szeregu Fouriera
- Strzałka ugięcia pręta jest skończona i niezerowa , na skutek przemieszczeń i obrotów przekrojów na podporach.
W dalszej części dodatku C rozważymy kilka przypadków szczegółowych.
Nieliniowy geometrycznie pręt wspornikowy
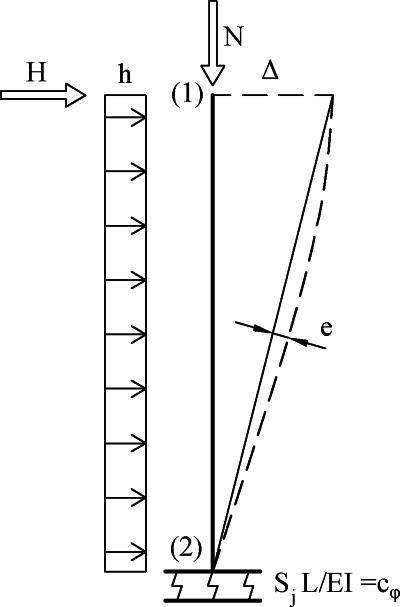
Ściskany pręt wspornikowy obciążony jest poprzecznie siłą H w wierzchołku (1) lub obciążeniem równomiernie rozłożonym h po wysokości. Pręt jest sprężyście utwierdzony w węźle dolnym (1) ze stałą sprężystości $c_\varphi$. -rys. C.2.
Warunki brzegowe można zapisać w postaci:
$$\begin{equation} u_2=0, \quad w_2=0, \quad M_2= -C_{\varphi} \cdot \varphi_2 \label {C.21} \end {equation} $$
W przypadku konstrukcji jednoelementowej macierz ($ \ref{C.11}$) jest macierzą konstrukcji i można ją bezpośrednio modyfikować w celu uwzględnienia warunków brzegowych ($ \ref{C.21}$). Modyfikację macierzy sztywności dokonamy poprzez wykreślenie wierszy i kolumn , odpowiadających odebranym stopniom swobody i bezpośrednie wpisanie warunku sprężystej podpory do równania kanonicznego. W rezultacie otrzymamy macierz zmodyfikowaną $[\widetilde{K]}$:
$$\begin{equation} [ \widetilde{K]} = \cfrac{EI}{L}
\begin{bmatrix}
\cfrac{EA}{EI} & 0 & 0 & 0 \\
& \cfrac{12 }{L^2} \Lambda_1 & \cfrac{6}{L} \Lambda_2 & \cfrac{6}{L} \Lambda_2 \\
& & 4 \Lambda_3 & 2 \Lambda_4 \\
& SYM & & 4 \Lambda_3+ c_{\varphi} \\
\end{bmatrix}
\begin{matrix}
u_2 \\ w_2 \\ \varphi_2 \\ \varphi_1
\end {matrix}
\label {C.22} \end {equation} $$
Poprzez odwrócenie macierzy ($\refC.22}$) uzyskujemy macierz podatności nieliniowego geometrycznie wspornika:
$$\begin{equation} [ \widetilde{K]}^{-1} = \cfrac{L}{\Theta}
\begin{bmatrix}
\cfrac{\Theta}{EA} & 0 & 0 & 0 \\
& k_{22} & k_{24}+\Lambda_2 \cdot c_{\varphi}\cdot L/2 & k_{24} \\
& & 3 \Lambda_2^2 -\Lambda_1(4 \Lambda_3+c_{\varphi}) & -3\Lambda_2^2 +2 \Lambda_1 \Lambda_4 \\
& SYM & & 3 \Lambda_2^2 -4 ] \Lambda_1 \Lambda_3 \\
\end{bmatrix}
\begin{matrix}
u_2 \\ w_2 \\ \varphi_2 \\ \varphi_1
\end {matrix}
\label {C.23} \end {equation} $$
gdzie:
$c_{\varphi}=C_{\varphi} \cdot L/EI$,
$k_{24}=\Lambda_2L(2\Lambda_3-\Lambda_4)$,
$k_{22}=-\cfrac{L^3}{3}\cdot(4\Lambda_3^2-\Lambda_4^2+\Lambda_3c_{\varphi} ) $,
$\Theta = – 4EI \cdot [(2\Lambda_3 -\Lambda_4) \cdot \Lambda_1 (2 \Lambda_3 + \Lambda_4) – 3\Lambda_2^2] + c_{\varphi} \cdot L \cdot ( 3 \Lambda_2^2 – 4 \Lambda_1 \Lambda_3) $.
Przemieszczenia i siły przekrojowe we wsporniku zostały przeanalizowane w treści podręcznika. Przemieszczenia węzłowe uzyskano poprzez przemnożenie macierzy podatności $(\ref{C.23}$) przez wektor równoważników węzłowych, który w przypadku obciążenia rozłożonego h, wynosi
$$\begin{equation} [F]_h = \cfrac{hL}{2} \cdot [\quad 0 \quad 1 \quad L/6 \quad -L/6 \quad ] \label {C.24} \end {equation} $$
a w przypadku obciążenia skupionego H, wynosi
$$\begin{equation} [F]_H = [ \quad 0 \quad H \quad 0 \quad 0 \quad ] \label {C.25} \end {equation} $$
Moment zginający w utwierdzeniu wspornika otrzymano po dodaniu do odpowiedniej współrzędnej wektora siły przywęzłowej, uzyskanej z przemnożenia wektora przemieszczeń węzłowych przez ostatni wiersz pierwotnej macierzy sztywności.
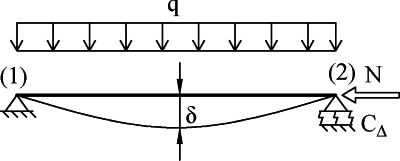
Nieliniowa geometrycznie belka wolnodparta
Warunki brzegowe dla belki wolnopodpartej (belki-słupa, pokazanego na C.3 są następujące
$$\begin{equation} u_1=0, \quad w_1=0, \quad T_2= -C_{\Delta} \cdot u_2 \label {C.26} \end {equation} $$
gdzie: $C_\Delta$ jest stała sprężystości podparcia w węźle prawym (2).
Belkę potraktujemy, jako jeden element, a strzałkę ugięcia wyznaczymy z zależności wyprowadzonych w poprzednim rozdziale. Zmodyfikowana macierz sztywności belki-słupa wynosi:
$$\begin{equation} [ \widetilde K] = \cfrac{EI}{L}
\begin{bmatrix}
4 \Lambda_3 & 0 & \cfrac {-6 \Lambda_2} {L} & 2 \Lambda_4 \\
& \cfrac {EA}{EI} & 0 & 0 \\
&& \cfrac{12 \Lambda_1 + c_{\Delta}} {L^2} & \cfrac { – 6\Lambda_2}{L} \\
& SYM & \cfrac{ -6 \Lambda_2}{L} & 4 \Lambda_3 \\
\end{bmatrix}
\begin{matrix}
\varphi_1 \\u_2 \\ w_2 \\ \varphi_2
\end {matrix}
\label {C.27} \end {equation} $$
Odwrotność macierzy zmodyfikowanej wynosi:
$$\begin{equation} [ \widetilde K]^{-1} = \cfrac{EI}{L}
\begin{bmatrix}
k_{11} & 0 & 3 L \cdot \Lambda_2 & k_{14} \\
0 & \cfrac {\Theta} {EA} & 0 & 0 \\
& & L ( 2 \Lambda_3+\Lambda_4 ) & 3 L \cdot \Lambda_2 \\
& SYM & & k_{11} \\
\end{bmatrix}
\begin{matrix}
\varphi_1 \\u_2 \\ w_2 \\ \varphi_2
\end {matrix}
\label {C.28} \end {equation} $$
gdzie:
$c_\Delta= C_\Delta \cdot \cfrac{L^3}{EI}$,
$k_{11}= \cfrac{-9\Lambda_2^2 +(c_\Delta + 12 \Lambda_1 ) \Lambda_3}{2 \Lambda_3 -\Lambda_4}$,
$k_{44}=\cfrac{18 \Lambda_2^2 – (c_\Delta + 12 \Lambda_1 ) \Lambda_4}{4 \Lambda_3 -2 \Lambda_4}$,
$\Theta=EI\cdot [36 \Lambda_2^2 -(12\Lambda_1 +c_\Delta) \cdot (2 \Lambda_3 +\Lambda_4)]$.
Siły węzłowe od obciążenia rozłożonego q
$$\begin{equation} [F]_q = \cfrac{qL}{2} [ \quad L/6 \quad 0 \quad 1 \quad – L/6 \quad ] \label {C.29} \end {equation} $$
Z formuły ($\ref {C.19}$) można wyznaczyć ścisłą strzałkę ugięcia pręta od obciążenia ściskającego $N$ bez udziału sił poprzecznych.
$$\begin{equation} f_N =w_N (\xi=0,5) = \cfrac{qL^4}{48EI} \cdot \left ( \cfrac{12 (2 \Lambda_3 + \Lambda_4)}{36 \Lambda_2^2 +(12 c_\Delta \Lambda_1) \cdot (2 \Lambda_3 +\Lambda_4)} +\cfrac{\alpha \cdot tg(\alpha/2)}{2 \Lambda_3 +\Lambda_4 } \right) \label {C.30} \end {equation} $$
Strzałką ugięcia pochodząca od sił poprzecznych jest całką szczególną zagadnienia, która powinna być dodana do ($\ref{C.30}$). W przypadku obciążenia równomiernie rozłożonego całka szczególna wynosi [2]:
$$\begin{equation} w_q (\xi) = \cfrac{qL^4}{24 EI} \to f_q= w(\xi=0,5)= \cfrac{q L^4}{384 EI} \label {C.31} \end {equation} $$
Element krzywoliniowy, sinusoidalny
Macierz podatności elementu, którego oś jest opisana ogólną zależnością parametryczną
$$\begin{equation} x=x(s) \quad y=y(s) \label {C.32} \end {equation} $$
podał [2] w postaci
$$\begin{equation} [ K]^{-1} =
\begin{bmatrix}
\int \limits_0^L \left ( \cfrac{(dx/dy)^2}{EA}+\cfrac{y^2}{EI} \right ) ds & \int \limits_0^L \left ( \cfrac{(dx/dy) (dy/ds)} {EA}- \cfrac{xy}{EI} \right ) ds & \int \limits_0^L \cfrac{y}{EI} ds \\
& \int \limits_0^L \left ( \cfrac{(dy/ds)^2} {EA}- \cfrac{x^2}{EI} \right ) ds & – \int \limits_0^L \cfrac{x}{EI} ds \\
& SYM & \int \limits_0^L \cfrac{1}{EI} ds \\
\end{bmatrix}
\label {C.33} \end {equation} $$
gdzie: $A(s)$ i $I(s)$ – pole przekroju i moment bezwładności sa znanymi funkcjami współrzędnej bieżącej s
Kształt elementu wstępnie wygiętego w łuk sinusoidy opisany w standardowym układzie współrzędnych (x,y)
$$\begin{equation} y= \eta \sin{(\omega x)} \label {C.34} \end {equation} $$
gdzie: $\eta$ – amplituda, $\omega= \cfrac{ n \ pi x}{L}$ – częstotliwość dla $n=1,2,3,…$ – liczba naturalna oznaczająca numer postaci własnej elementu,
Równanie krzywej ($\ref{C.34}$) można zapisać w postaci parametrycznej:
$$\begin{equation} y= \eta \sin {\alpha} ; \quad x =\cfrac{\alpha}{\omega} \label {C.35} \end {equation}$$
gdzie parametr $\alpha \in [ \quad \alpha_1= -\omega L/2 ; \quad \alpha_2= \omega L/2 \quad ]$,
Poszczególne wyrazy macierzy podatności $( \ref{C.32}$) wynoszą:
$k_{11}= \int \limits_0^L \left ( \cfrac{(dx/dy)^2}{EA}+\cfrac{y^2}{EI} \right ) ds=\int \limits_{\alpha_1}^{\alpha_2} \left ( \cfrac{(dx/dy)^2}{EA}+\cfrac{y^2}{EI} \right ) d \alpha= \cfrac{ \eta ^2 [ n \pi – \sin {(n \pi) ] } }{2EI}$,
$k_{12}= \int \limits_{\alpha_1}^{\alpha_2} \left ( \cfrac{(dx/dy) (dy/ds)} {EA}- \cfrac{xy}{EI} \right ) d \alpha = \cfrac{ \eta L [ n \pi \cdot \cos {(n \pi /2) } – 2 \sin{(n \pi / 2)]} }{n \pi \cdot EI }$,
$k_{22}= \int \limits_{\alpha_1}^{\alpha_2} \left ( \cfrac{(dy/ds)^2} {EA}- \cfrac{x^2}{EI} \right ) d \alpha = \cfrac{L}{12} \left ( \cfrac{6 \eta^2 [ n \pi +\sin{(n \pi) ] }}{EA}+\cfrac{L^2 \cdot n \pi}{EI}\right )$,
$k_{13}= \int \limits_{\alpha_1}^{\alpha_2} \cfrac{y}{EI} d \alpha =0$,
$k_{23}= \int \limits_{\alpha_1}^{\alpha_2} \cfrac{-x}{EI} d \alpha =0$,
$k_{33}= \int \limits_{\alpha_1}^{\alpha_2} \cfrac{1}{EI} d \alpha = \cfrac{n \pi}{EI}$,
Macierz sztywności uzyskamy przez odwrócenie macierzy podatności. Stosunkowo proste wyrażenie uzyskamy dla kształtu pręta proporcjonalnego do pierwszej postaci własnej, czyli dla n=1:
$$\begin{equation} [ K] = \cfrac{1}{\Theta}
\begin{bmatrix}
2 \pi^3 EI ( EA L^2/ \eta +6EI \cdot \eta & 48 \pi L \cdot EA \cdot EI & 0 \\
& 12 \pi^3 EA \cdot EI \cdot \eta & 0 \\
& SYM & EI \Theta / \pi \\
\end{bmatrix}
\label {C.36} \end {equation} $$
gdzie: $\Theta= \eta [ EA L^2 (\pi^2 -96) +6EI \pi^4 \eta^2 ]$Literatura
- Chodor, L. (2013). Belka Timoshenko na sprężystym-podłożu. PiWiki – Inżynierowie i Architekci Chodor-Projekt, [ https://chodor-projekt.net/encyclopedia/belka-timoshenko-sprezyste-podloze/ ]
- Livesley R. K. (1975), Matrix methods of structural analysis, Pergamon Press [http://books.google.com/books?id=tYsoAQAAMAAJ ]
________________________________