Artykuł w ciągu ostatnich 24 godzin czytało 1 Czytelników
[Imperfekcje projektowe z odchyłek wykonawczych] ⇐ ⊗ ⇒ [Imperfekcje konstrukcji, a współczynniki bezpieczeństwa]
Formuła Ayrton i Perry (AFP) [1] jest podstawą współczesnej formacji współczynników wyboczeniowych mimo, że została wyprowodzona dla pręta idealnie sprężystego, obarczonego zdetermniowaną imperfekcją. Najnowsze badania uogólniają fomułę AFP poprzez wprowadzenie teorii alternatywnej amplitudy imperfekcji. Rzeczywiste konstrukcje pracują w zakresie sprężysto-plastyczym, a imperfekcje mają charakter losowy.
-
-
-
-
- Powyżej krzywej Shanleya 1 nie są możliwe stany równowagi. Krzywa Shanleya stanowi ograniczenie od góry wszystkich ścieżek równowagi prętów rzeczywistych z mimośrodami i imperfekcjami
- Wygięcia boczne pręta rzeczywistego (mimośrodowo ściskanego lub z imperfekcjami) przebiegają od początku ścieżki równowagi, a nie od momentu osiągnięcia siły krytycznej zgodnie z teorią modułu stycznego. Poszukiwanie klasycznej siły krytycznej nie jest potrzebne przy analizie rzeczywistych prętów. Wymagana jest analiza konstrukcji obarczonej imperfekcjami wg teorii geometrycznie nieliniowej – dla systemów nie przechyłowych wystarcza analiza 2 rzędu (P-Δ). Na podstawie tej analizy uzyskujemy nośności ułożone na krzywej 2
-
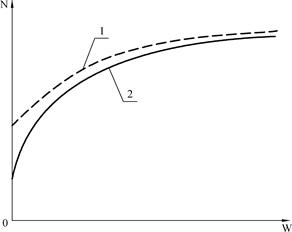
Rys. 2-3.12. Ścieżki równowagi ściskanego pręta: 1 – pręt osiowo ściskany (Shanleya), 2 – pręt mimośrodowo ściskany
(opracowano na podstawie [zotpressInText item=”{R5U2NNFG}”] )
Koncepcja Shanleya jest krytyką idei siły krytycznej, klasycznie rozumianej, jako obciążenie bifurkacyjne prostego pręta ściskanego.
Koncepcja Hutchinson
W pracach [zotpressInText item=”{YQ82G67R}”], [zotpressInText item=”{G47BCX8L}”] pokazano, że w odniesieniu do plastycznej utraty stateczności konstrukcji obarczonych imperfekcjami, można stosować oszacowania asymptotyczne, uzyskiwane w duchu teorii[zotpressInText item=”{XCVSZUFT}”] układów sprężystych.
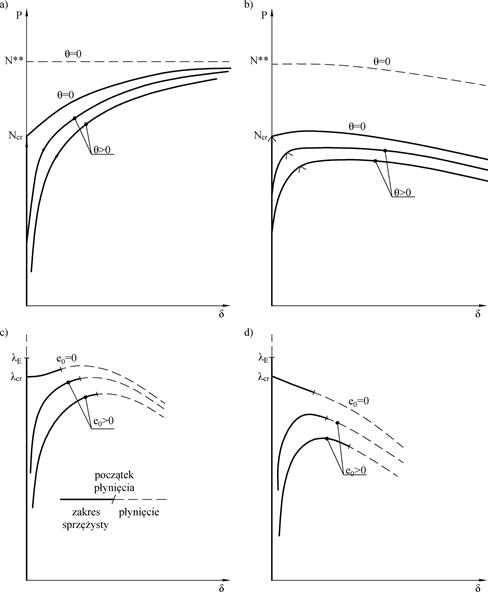
Rys. 2-3.13. Porównanie teorii Shanleya i Hutchinsona: a) klasyczny model Shanley, b), model przy dużych nieliniowościach c) teoria Hutchinsona – punkt bifurkacji symetryczny, d) teoria Hutchinsona – punkt bifurkacji niesymetryczny.
(opracowano na podstawie [zotpressInText item=”{YQ82G67R}”])
Na Rys. 2-3.13a, b linią przerywaną oznaczono linię nośności $n^{**}$ wg teorii zredukowanego modułu, a symbolami $∧$ oznaczono punkty na ścieżce równowagi odpowiadające zapoczątkowaniu odciążenia sprężystego, Liniami ciągłymi oznaczono ścieżki równowagi $P- e$, wynikające z teorii Shanleya dla pręta bez imperfekcji ($\Theta=0$ ) i z imperfekcjami ($\Theta>0 ).
Rys. 2-3.13 c, d przedstawiono ścieżki równowagi $\lambda – e$ przy zniszczenia elementu w zakresie plastycznym na skutek utworzenie przegubów plastycznych po utracie stateczności w zakresie sprężystym, analizowane przez Hutchinsona w pracach [zotpressInText item=”{YQ82G67R}”], [zotpressInText item=”{G47BCX8L}”].
Zmienna jest mnożnikiem obciążenia zewnętrznego, proporcjonalnie, do którego rośnie obciążenie P. Do celów porównawczych teorii Shanley i Hutchinson można przyjąć $\lambda=N$, – $\lambda_E$ – klasyczny mnożnik obciążenia Eulera, $\lambda_{cr}$ – mnożnik obciążenia bifurkacyjnego przy symetrycznym punkcie bifurkacji (Rys. 2-3.13 c) i przy niesymetrycznym punkcie bifurkacji (Rys. 2-3.13 d). Liniami ciągłymi oznaczono fragment sprężystej ścieżki równowagi, obserwowany do momentu utworzenia przegubu plastycznego (lub przegubów), który oznaczono kreską poprzeczną na styku z plastycznym fragmentem ścieżki równowagi, (linia przerywana). Praca elementu po utworzeniu mechanizmu plastycznego następuje na silnie opadającej ścieżce równowagi, to znaczy nawet przy zmniejszającym się obciążeniu następuje przyrost przemieszczeń $e$.
Nośność graniczna, czyli maksimum ścieżki równowagi może wystąpić (zależnie od rodzaju punktu bifurkacyjnego) na sprężystej lub plastycznej części ścieżki równowagi.
Nośność graniczna jest dość dobrze przewidywana, gdy maksymalne obciążenie zachodzi bardzo blisko punktu bifurkacji sprężystej, choć amplituda postaci wyboczenia jest słabo określona. Jeśli natomiast maksymalne obciążenie znacznie przekracza obciążenie bifurkacji to dokładność oszacowania nośności gwałtownie pogarsza się.
Proces tworzenia się przegubów plastycznych konstrukcji obarczonych imperfekcjami geometrycznymi w analizie GMNIA badano w pracy [zotpressInText item=”{2AITV5UB}”], gdzie pokazano, że krytyczne (prowadzące do zniszczenia plastycznego) imperfekcje geometryczne występują z udziałem naprężeń resztkowych i trwałych, wstępnych imperfekcji geometrycznych
Krzywe wyboczeniowe a dokładne rozwiązanie sprężysto-plastyczne
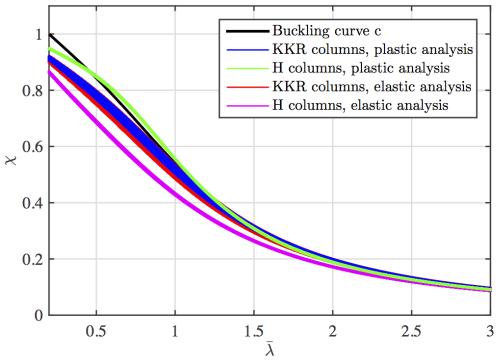
W pracy [zotpressInText item=”{G5C4W4TR}”] przeprowadzono testy zależności Eurokod z wykorzystaniem programu ABAQUS i pokazano, że obliczenia prowadzone z uwzględnieniem modelu plastycznego materiału – systematycznie prowadzą do większych współczynników wyboczeniowych od analizy sprężystej, szczególnie w zakresie sprężysto-plastycznego wyboczenia dla prętów o smukłości $\overline \lambda <1$ . Różnica dochodzi do kilkudziesięciu procent. Na rys. 2-3.14 pokazano przykładowe wyniki dla prętów z rur kwadratowych KKR oraz dwuteowników szerokostopowych H.
-
Alternatywna amplituda imperfekcji
Skalowanie pierwszej postaci wyboczenia sprężystego
Wielu badaczy [zotpressInText item=”{EGXCE73Y}”],[zotpressInText item=”{Y5ZFS8VA}”], [zotpressInText item=”{RYPSP94P}”],[ zotpressInText item=”{EKVJ7CVX}”] przyjmuje, imperfekcje w kształcie pierwszej formy wyboczenia sprężystego. W tym celu najpierw jest prowadzona klasyczna analiza LBA na idealnym modelu konstrukcji (w konfiguracji nieodkształconej i niezaburzonej imperfekcjami), a następnie odbywa się skalowanie kształtu wyboczenia otrzymanego dla pierwszej wartości krytycznej, tak, aby utworzyć początkową imperfekcję. Koncepcja tej teorii wynika z hipotezy, że najniekorzystniejsza geometria imperfekcji jest najbliższa pierwszej postaci krytycznej, ponieważ wymaga najmniejszej energii odkształcania i najkrótszą drogą prowadzi do ostatecznego zniszczenia.
W większości przypadków pierwsza postać wyboczenia może reprezentować kształt zniszczenia i imperfekcje zgodne z tym kształtem wspomagają zniszczenie. Jednakże są też pewne systemy, dla których postać zniszczenia różni się od pierwszej formy wyboczenia. Ponadto szerokie badania statystyczne wskazują, że rzeczywiste kształty imperfekcji prawie zawsze różnią się od krzywych wynikających ze sprężystych postaci wyboczenia, czyli w uproszczeniu od kształtu sinusoidy (np. [zotpressInText item=”{E93IL3SI},{XCNR72RY}”]).
Wskazuje się, że taka metoda nie jest wiarygodna we wszystkich przypadkach, ponieważ na poprawność modelu nie przeprowadzono niebudzącego wątpliwości dowodu. Nie pokazano, że na dającym się zaakceptować poziomie prawdopodobieństwa zniszczenia metoda skalowania pierwszej postaci wyboczenia, będzie prowadziła do poprawnego oszacowania obliczeniowej nośności konstrukcji.
[zotpressInText item=”{2AITV5UB}”] zaproponowali, by kształt imperfekcji łukowej określać z uwzględnieniem zachowania konstrukcji w zakresie plastycznym ze względu na istotny wpływ naprężeń resztkowych i faktyczne zniszczenie plastyczne, zapoczątkowane wyboczeniem sprężystym (p. pkt 2-3.1.4). W tym ujęciu sprawczy kształt imperfekcji jest wyznaczany w trakcie rozwiązania problemu, a krytyczny kształt sprężysty jest tylko pierwszą iteracją. W istocie rozróżnia się, więc dwa pojęciowo różne rodzaje wstępnych imperfekcji konstrukcji:
- rzeczywiste, wyznaczone w drodze pomiarów
- obliczeniowe, to znaczy takie zastępcze imperfekcje nierzeczywiste, które są przyjmowane w obliczeniach, i które sprawiają, że wyznaczona nośność graniczna konstrukcji przybliża się do nośności rzeczywistej. Imperfekcje sprężyste zgodne z postacią wyboczenia mogą być wstępnym punktem startu w analizie nieliniowej, podczas której przekształcą się w inny kształt, odpowiadający mechanizmowi zniszczenia sprężysto-plastycznego.
Hipoteza Chladný
Eugen Chladný w pracy doktorskiej [zotpressInText item=”{KYHK3YFJ}”] i habilitacyjnej [zotpressInText item=”{47PYRHBD}”] opracował podstawy Alternatywnej Metody Imperfekcji Geometrycznych (AIM) i w 2000 roku zaproponował tę metodę w bardziej ogólnej formie do zastosowania w normie Eurokod 3. Metoda została zaakceptowana w projekcie prEN1993-1-1 (czerwiec 2002) i wprowadzona w pkt 5.3.2 (11) do oficjalnej wersji EN1993-1-1 (2005). Rozszerzona wersja metody AIM jest stosowana w narodowej normie słowackiej STN EN 1993-1-1 /NA (2007), a także w pkt. 5.3.2 (11) normy europejskiej do projektowania konstrukcji aluminiowych.
Metoda jest wyczerpująco opisana w pracach [zotpressInText item=”{GP8NVQPC}”], [zotpressInText item=”{HJNGPFXK}”, [zotpressInText item=”{HVQU2YMJ}”].
W literaturze można spotkać się z nazwą metody UGLI (Unique Global and Local Initial imperfection) [zotpressInText item=”{V63L488G}”] lub EUGLI (Equivalent Unique Global and Local Initial imperfection”) [zotpressInText item=”{HVQU2YMJ}”]. Metoda pierwotnie opracowana na przypadek elementów o stałym przekrojów, ściskanych stałą siła osiową, jest stopniowo uogólniana na:
- elementy o zmiennym przekroju i sile osiowej po długości [zotpressInText item=”{V63L488G}”] ,
- łuki trójpunktowe (basket handle arch type) w słowackim aneksie normy ,
- klasę 4-tą przekroju elementu Brodniansky J., Rudolf Ároch R. , (2014), Unique global and local initial imperfection in the shape of the elastic buckling mode (Application of “UGLI” imperfection method for frames with class 4 cross-sections), IASS-SLTE Symposium 2014: Shells, Membranes and Spatial Structures, Brasilia, Brazil, Sep 2014,
W podejściu AIM przyjmuje się hipotezy Chladný AIM 1 i AIM 2:
AIM 1 Kształt wstępnych imperfekcji $\eta_{ini}$ jest proporcjonalny do postaci wyboczenia sprężystego systemu $\eta_{cr}$:
$$ \begin {equation} \eta_{ini} (x) = e_{0,m} \cdot \eta_{cr} (x) \label {2-3.2a7} \end {equation}$$
gdzie $ e_{0,m}$ jest zastępczą (równoważną, alternatywną) amplitudą imperfekcji, podczas gdy $\eta_{cr}(x)$ jest funkcją postaci wyboczenia elementu unormowaną w taki sposób, że jej amplituda jest jednostkowa $|\eta_{cr,max}|=1$. Z wielu postaci wyboczenia systemu należy stosować najniekorzystniejszą, którą najczęściej jest pierwsza postać wyboczenia [zotpressInText item=”{V63L488G}”], [zotpressInText item=”{BNRVDPL5}”] .
AIM 2 Imperfekcje alternatywne (2.49) opisują łącznie lokalne i globalne (zintegrowane) imperfekcje.
Wbrew temu co postulują prace [zotpressInText item=”{KWXIPYDU}”], [zotpressInText item=”{RR66824E}”], przyjmujemy że jednocześnie nie wystąpią różne formy wyboczenia konstrukcji i nie należy tych postaci kombinować. Zasadę można uzasadnić w sposób niebudzący wątpliwości w języku prawdopodobieństwa zdarzeń wykluczających.
Alternatywna amplituda imperfekcji $ e_{0,m} $ jest taką zastępczą (równoważną rzeczywistej) amplitudą imperfekcji, która stanowi mnożnik (skalę) dla funkcji sprężystej postaci wyboczenia elementu.
Ideę metody AIM przedstawiono na przykładzie pręta utwierdzono-przegubowego o długości L i stałych po długości charakterystykach $A, \, I_y, \, E$ , ściskanego stałą siłą osiową $N_{Ed} $ . Na Rys. 2-3.15 zilustrowano zasadnicze pojęcia metody alternatywnej w odniesieniu do м-tego przekroju sprawczego o współrzędnej $x_m$.
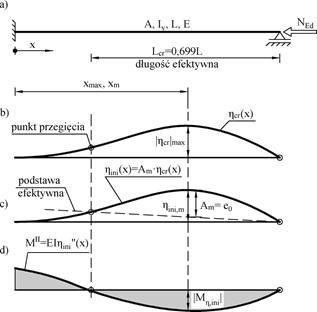
Rys. 2-3.15. Metoda alternatywna AIM: a) schemat pręta, b) postać wyboczenia , c) imperfekcje alternatywne , d) wykres momentów zginających . Linia przerywana (podstawa efektywna) łączy punkty przegięcia , czyli określa długość efektywną elementu . Imperfekcja (normowa, statystyczna) jest przyrównywana do rzędnej ugięcia w przekroju sprawczym м nad podstawą efektywną
(opracowano na podstawie [zotpressInText item=”{BNRVDPL5}”])
Na rys. 2-3.14b wykreślono funkcję$ \eta_{cr}(x)$ , która jest unormowaną funkcją postaci sprawczej wyboczenia sprężystego układu (pręta lub systemu prętów). Postacią sprawczą jest podstawowa (pierwsza) postać wyboczenia, którą obserwuje się przy najmniejszym krytycznym mnożniku konfiguracji obciążenia. Inna postać wyboczenia, (ale również pierwsza) może dotyczyć innej konfiguracji obciążenia (lub innego schematu pręta, np. po utworzeniu przegubu plastycznego). Unormowanie funkcji polega na takim przeskalowaniu funkcji, by amplituda
Na rys. 2-3.14c wykreślono funkcję , która jest alternatywną (zastępczą, równoważną) zintegrowaną (łącznie globalną i lokalną) funkcją imperfekcji układu o amplitudzie . Linią przerywaną oznaczono podstawę efektywną, łączącą punkty przegięcia funkcji imperfekcji, czyli punkty zerowe momentu zginającego , odpowiadające tej linii ugięcia. Z warunku proporcjonalności (2.49) wynika, że punkty przegięcia sprawczej funkcji wyboczenia występują dla tych samych rzędnych i długość efektywną można oszacować na podstawie
Normowa (statystycznie określona) amplituda imperfekcji jest strzałką linii ugięcia , liczoną, jako odległość od podstawy efektywnej do linii ugięcia.
Na rys. 2-3.14d, wykreślono funkcję momentu zginającego , odpowiadającą kształtowi wyboczenia . Wartość bezwzględna momentu w przekroju m jest wartością ekstremalną . Z tego warunku wyznacza się położenie punktu м. Oczywiście odpowiada ono również ekstremum momentu wynikającego z krzywej postaci wyboczenia: .
Metoda AIM uwzględniania geometrycznych imperfekcji konstrukcji jest metodą alternatywna w stosunku do stosowania współczynników wyboczeniowych oraz tak zwanej metody ogólnej [zotpressInText item=”{TSFWTQGW}”] i staje się podstawową metodą w projektowaniu konstrukcji, dlatego jej idee są ważne dla projektantów. W metodzie AIM imperfekcje geometryczne (globalne i lokalne) odpowiadają skalowanej formie sprężystego wyboczenia, stowarzyszonego z wektorem własnym uzyskanym z liniowej analizy wyboczeniowej (LBA) całego układu konstrukcyjnego. Metoda alternatywna AIM bazuje więc na omówionej w punkcie 2-3.2.1 metodzie skalowania pierwszej postaci wyboczenia sprężystego.
Analiza LBA (rozwiązania problemu własnego) zaimplementowana we wszystkich pakietach numerycznych jest efektywna (mało kosztowna) i może być zastosowana do dowolnie złożonej konstrukcji. Analiza całego układu bez wydzielania elementów pozwala ujawnić wszystkie możliwe postacie wyboczenia, a w szczególności postacie globalne (przechyłowe lub przeskok) i lokalne (łukowe) w tym ich fizycznie możliwe kombinacje. W zależności od typu elementów skończonych ujawnia też rozmaite rodzaje utraty stateczności (wyboczenie giętne, boczne (zwichrzenia), skrętne, płytowe, powłokowe, itd.) oraz ich fizycznie możliwe kombinacje (interakcję). W istocie postacie i rodzaje utraty stateczności są sprzężone i nie należy dążyć do ich rozprzężenia często tylko po to, by nazwać je, a następnie zastosować uproszczone, normowe zasady interakcyjne.
Uogólnienie formuły Ayrton-Perry
Uogólnienie na zwichrzenie pręta
W 1991 roku w pracy zotpressInText item=”{QVU3L9BH}”] podjęto próbę uogólnienia formuły Ayrton-Perry APF na przypadek zwichrzenia pręta w drodze skalibrowania formuły pierwotnej do wyników eksperymentalnych. W późniejszej wersji Eurokod [zotpressInText item=”{TSFWTQGW}”] zaimplementowano zmodyfikowaną wersję tej formuły. W pracy [zotpressInText item=”{TSFWTQGW},{FFCMR2PW}”] wyprowadzono teoretycznie formułę APF na przypadek skręcania i zwichrzenia prętów.
W pracy [zotpressInText item=”{52IXD6L3}”] ustalono niezbędne warunki dla spójnego uogólnienia APF dla problemu zwichrzenia belek zginanych i ściskanych stałą siłą.
Naprężenia w przekroju sprawczym zginanym momentem zginającym $M_y$ względem osi większej sztywności, momentem drugiego rzędu $M_z^{II}$ względem osi słabszej oraz paczonych bimomentem drugiego rzędu $B^{II}$ wyznaczano z ogólnej zależności:
$$ \begin {equation} \sigma=\cfrac{M_y}{W_y}+ \cfrac {M_Z^{II}}{W_z}+\cfrac{B^{II}}{W_\omega}=f_y \label {Papp1} \end {equation}$$
gdzie $W_y$, $W_z$ oraz $W_\omega$ są wskaźnikami wytrzymałości przekroju względem osi „y” i „z” oraz wskaźnikiem wytrzymałości giętno- skrętnej „$\omega$”.
Zagadnieniem zwichrzenia rządzi formuła APF analogiczna do ($\ref{2-3.5}$) z rozwiązaniem ($\ref{2-3.6}$), ale konsekwentnie w miejsce współczynnika wyboczeniowego $\chi$ należy podstawić współczynnik zwichrzenia $\chi_{LT}= \cfrac{M_y}{M_R}$,a w miejsce smukłości względnej $\overline \lambda$ smukłość na zwichrzenie $\overline \lambda_{LT} =\sqrt{\cfrac{M_R}{M_{ce}}}$ , gdzie $M_R=W_y\cdot f_y$.
Parametr imperfekcji ($\ref{2-3.2a}$) dla zwichrzenia wynosi
$$ \begin {equation} \Theta_{LT}= \cfrac{W_y}{W_\omega} \cdot \left [ v_0 + \varphi_0 \left( \cfrac{W_\omega }{W_z} – \cfrac{GI_T}{M_{cr}} \right ) \right ] \label {Papp2} \end {equation}$$
gdzie $v_0$ oraz $\varphi_0$ amplitudy imperfekcji : wygięcia bocznego oraz kąta skręcenia przekroju elementu.
Kompletną analizę zagadnienia APF dla słupów-belek przedstawiono w pracy [zotpressInText item=”{PBJNCN56}”]. Rozwiązanie [zotpressInText item=”{52IXD6L3}”] rozszerzono na dowolne rozkłady momentów zginających. Pokazano, że zaproponowana procedura projektowania jest lepsza od formuł interakcji normy [zotpressInText item=”{TSFWTQGW}”] (metoda 2).
Należy zwrócić uwagę, że z formuły ($\ref{Papp2}$) można ocenić parametr imperfekcji w przypadku zwichrzenia dla znanych imperfekcji projektowych, wyznaczonych z tolerancji wykonawczych.
Formuła APF przy jednoczesnym wyboczeniu i zwichrzeniu
W pracy [zotpressInText item=”{52IXD6L3}”] przedstawiono rozwiązanie problemu fundamentalnego: korelacji ściskania ze zginaniem z uwzględnieniem wyboczenia giętnego oraz bocznego (zwichrzenia). Parametry tego problemu oznaczono indeksami BC( Buckling-Compression)
Formułę APF dla problemu BC można zapisać w postaci
$$ \begin {equation} \chi_{BC}^2 + \chi_{BC} \cdot \left [ -\beta_N – \cfrac{1}{ \overline \lambda_{BC}^2} \left( 1-\Theta \right) \right ] +\cfrac{1}{ \overline \lambda_{BC}^2} \beta_N = 0 \label {Papp3} \end {equation}$$
gdzie uogólniony parametr imperfekcji jest parametrem ($\ref{Papp2}$) zmodyfikowanym przez współczynniki amplifikacji:
$$ \begin {equation} \Theta_{LT}= \cfrac{W_y}{W_\omega} \cdot \left [ v_0 \cdot a_{\Lambda,z}+ \varphi_0 \cdot a_{\Lambda,x} \left( \cfrac{W_\omega }{W_z} – \cfrac{GI_T}{M_{cr}} \right ) \right ] \label {Papp4} \end {equation}$$
Współczynniki amplifikacji można wyznaczyć z zależności:
$$ \begin {equation} a_{\Lambda,x}= \cfrac{1}{1-1/\Lambda_{cr,x}} \quad ; \quad a_{\Lambda,z}= \cfrac{1}{1-1/\Lambda_{cr,z}}\label {Papp5} \end {equation}$$
gdzie:
$\Lambda_{cr,x}=\cfrac{N_{cr,x}}{N}$ – mnożnik krytyczny przy czystym wyboczeniu skrętnym,
$\Lambda_{cr,z}=\cfrac{N_{cr,z}}{N}$ – mnożnik krytyczny przy czystym wyboczeniu giętnym względem osi z,
$N_{cr,z}=\cfrac{EI_z \pi^2}{L^2}$,
$N_{cr,x}= \cfrac{1}{r_0^2}\left( \cfrac{EI_\omega \pi^2}{L^2} +GI_T\right)$Współczynnik korelacji zginania ze ściskaniem (współczynnik udziału ściskania) wynosi:
$$ \begin {equation} \beta_N =1-n+m_z^{II}+b^{II} \label {Papp6} \end {equation}$$
gdzie $n=\cfrac{N}{N_R}$, $m_z^{II} = \cfrac{M_z^{II}} {M_{R,z}}$, $b^{II}=\cfrac{B^{II}}{B_R}$ są względnymi siłami przekrojowymi: siłą osiową, zginającym momentem względem osi „z” drugiego rzędu oraz bimomentem drugiego rzędu. Siły względne są odniesione do nośności przekroju: $N_R=N_{pl} A \cdot f_y$, $M_{R,z}=W_z\cdot f_y$, $B_R=W_\omega\cdot f_y$, gdzie $A$ – pole przekroju, $W_z$ – wskaźnik wytrzymałości względem osi słabszej, $W_\omega$ – wycinkowy wskaźnik wytrzymałości.
Współczynnik korelacji najprościej wyznaczać dla sił uzyskanych z rozwiązania drugiego rzędu od wymuszeń imperfekcji. Można też oszacować je w przybliżeniu z zależności:
$$ \begin {equation} M_z^{II}=M_{z,0} \cdot a_{\Lambda,z} =N\cdot v_0\cdot a_{\Lambda,z} \label {2-3.50} \end {equation}$$
$$ \begin {equation} B^{II}= \varphi_0\cdot a_{\Lambda,x} \cdot \left [ N\cdot r_0^2 -GI_T \cdot \left (1-\cfrac{1}{ a_{\Lambda,x}} \right )\right ] \label {2-3.51} \end {equation}$$
Zalezności ($\ref{Papp3}$) do $\ref{Papp5}$) są prawdziwe wówczas, gdy wygięcie wstępne $v_0$ oraz wstępny kąt skręcenia $\varphi_0$ spełniają zależność
$$ \begin {equation} \cfrac{v_0}{\varphi_0}=\cfrac{M_{cr}}{N_{cr,z}}=r_0 \sqrt{\cfrac{N_{cr,x}}{N_{cr,z}}} \label {2-3.52} \end {equation}$$
gdzie $r_0$ jest biegunowym promieniem bezwładności przekroju.
Rozwiązaniem równania kwadratowego APF również w przypadku interakcji zginania i ściskania przedstawiają formuły ($\ref{2-3.6}$), w których należy podstawić odpowiednie smukłości i parametr imperfekcji.
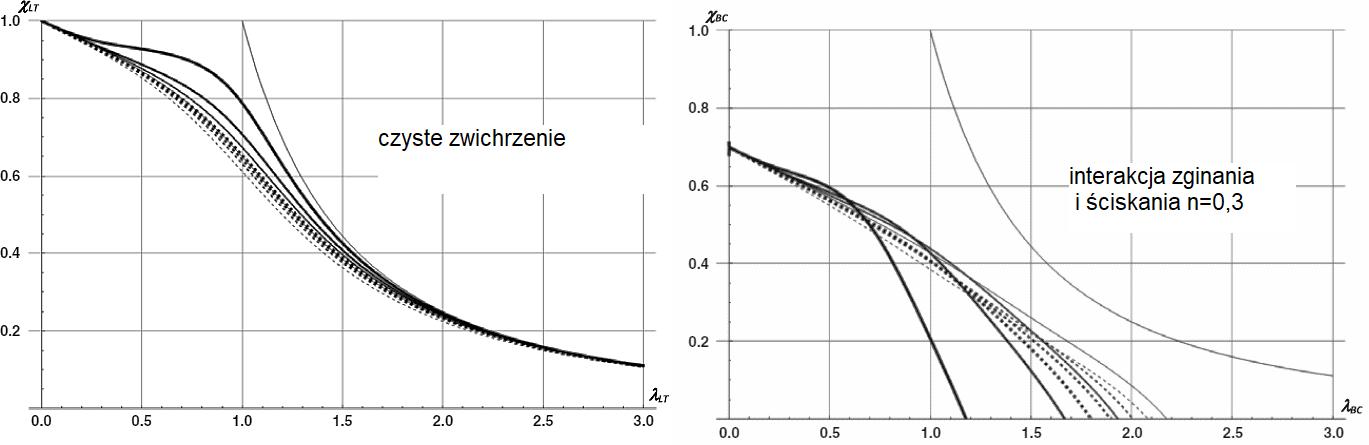
Z przedstawionych zależności wynika, parametr imperfekcji zależy od długości pręta oraz przekroju elementu. Funkcyjne zależności są dość złożone, co potwierdza, że zastosowanie teorii wyboczeniowej może prowadzić do słabych oszacowań wytężenia pręta. Z rys. 2-3.16 wynika, że przy interakcji zginania i ściskania zależność współczynnika wyboczeniowego od smukłości może przyjąć zupełnie inny kształt od krzywych normowych.Lepszym rozwiązaniem jest wyznaczenie momentu krytycznego $M_{cr,N}$ pręta, zmniejszonego wskutek jednoczesnego ściskania i wichrzenia zgodnie z fromuła interakcji:
$$ \begin {equation} M_{cr,N}=r_0\cdot \sqrt{(N_{cr,z}-N)\cdot (N_{cr,x}-N)}\label {2-3.53} \end {equation}$$
Hipoteza Papp dla zwichrzenia pręta
[zotpressInText item=”{Q9T67P6U}”] wyznaczył równoważną amplitudę dla postaci wyboczenia bocznego (zwichrzenia) poprzez uogólnienie podejścia [1] na sprzężony problem (ang. coupled) utraty stateczności pręta, tzn. wyboczenia giętnego sprzężonego z wyboczeniem skrętnym i wyboczeniem bocznym (zwichrzeniem). Matematycznie nie jest ściśle możliwe i praktycznie nie jest potrzebne rozdzielenie postaci wyboczenia giętnego, skrętnego oraz bocznego.
Rozwiązanie bazuje na fundamentalnym rozwiązaniu zagadnienia dla wyboczenia giętnego [zotpressInText item=”{35F2WZZR}”] , [zotpressInText item=”{35F2WZZR}”] i uogólnia je na przypadek zwichrzenia. [zotpressInText item=”{Q9T67P6U}”] założył mianowicie, że imperfekcje boczne belki są proporcjonalne do funkcji bocznego wyboczenia sprężystego odpowiadającej postaci bocznego wyboczenia sprężystego $\nu_{cr} (x)$.
Zależność na równoważne wstępne wygięcie boczne preta (imperfekcję boczną) $\nu_0(x)$ w funkcji obliczeniowej amplitudy bocznego wygięcia wstępnego (imperfekcji) $e_{0,z}$ oraz siły krytycznej (Eulera) dla przypadku wyboczenia z płaszczyzny pręta $N_{cr,z}$ zapisano w postaci:
$$ \begin {equation} v_0(x) =e_{0,z} \cdot \cfrac{N_{cr,z}}{EI_z \cdot {v^”}_{cr,max} } \cdot v_{cr} (x) \label {2-3.54} \end {equation}$$
Równoważne wstępne skręcenie wstępne (imperfekcja skręcenia) wynosi
$$ \begin {equation} \varphi_0 (x)= \cfrac{N_{cr,z} }{M_{cr}} \cdot v_0(x) \label {2-3.55} \end {equation}$$
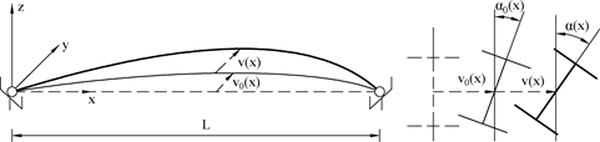
Formuła ($\ref{2-3.54}$) stanowi uogólnienie normowego wyrażenia na przypadek wyboczenia bocznego (zwichrzenia). Na Rys. 2-3.17 zilustrowano podstawowe zmienne modelu Pappa: – imperfekcje pręta: wygięcie boczne i kąt skręcenia odpowiednio; – wygięcie boczne i kąt skręcenia pręta po obciążeniu (w stosunku do kształtu z imperfekcjami).
W dobie powszechnej komputeryzacji, szczególnie interesujące jest zaproponowane iteracyjne ujęcie numeryczne zagadnienia.
(opracowano na podstawie [zotpressInText item=”{Q9T67P6U}”])
Formuła Szalai
W 2017 roku Szalai zaprezentował formułę amplifikacji imperfekcji geometrycznych dla belki-słupa, czyli pręta ściskanego, zginanego i skrecanego nieswobodnie podlegającego jednoczesnemu wyboczeniu giętnemu i zwichrzeniu. Uogólnioną formułę amplifikacji da się zapisać w postaci macierzowej [zotpressInText item=”{XZT6QNPE,wzór (23)}”]:
$$ \begin {equation} [u](x) =a_\Lambda \cdot [u]_0(x) \label {2-3.56} \end {equation}$$
gdzie:
$[u]_0(x) $ imperfekcje geometryczne prąta: wstępne skrócenia $u_0 (x)=0$, wygięcia w kierunku poprzecznym do pręta $v_0(x)$, ugięcia $ w_0(x)$ oraz skręcenia $\varphi_0(x)$ ujęte w wektor
$ [u]_0 (x)= \left [ \begin{array}{l}
0 \\
v_0(x)\\
w_0(x)\\
\varphi_0(x)
\end{array} \right] $$[u](x)$ całkowite przemieszczenie pręta w stanie II rzędu złożone z imperfekcji $[u[_0(x)$ oraz ich przyrostu wywołanego działaniem sił przekrojowych
$ [u] (x)= \left [ \begin{array}{l}
u(x) \\
v(x)\\
w(x)\\
\varphi(x)
\end{array} \right] $Współczynnik amplifikacji $a_{\Lambda}= \cfrac{1}{1-\tfrac{1}{\Lambda_{cr}}}$ zdefiniowano w rozdziale „Imperfekcyjna metoda. Pojęcia podstawowe” wzór (1-1.12),
przy czym mnożnik krytyczny $\Lambda_{cr}$ należy wyznaczać w analizie LBA całego ustroju na modelu uwzględniającym wszystkie badane postacie wyboczenia, czyli wyboczenie giętne, skrętne i giętno-skrętne (zwichrzenie). Takim modelem jest uogólniony pręt Własowa, to znaczy pręt o siedmiu stopniach swobody z paczeniem jako siódmym stopniem.
Formuła ($\ref{2-3.56}$) jest uogólnieniem klasycznej formuły amplifikacji ($\ref{2-3.22}$) i jest analogicznie wyprowadzona. Całość wyprowadzenia można znaleźć w pracy [zotpress items=”XZT6QNPE” style=”apa”].
Rys. 2-3.18 Ilustracja do formuły Szalai
[zotpressInText item=”{XZT6QNPE}”]
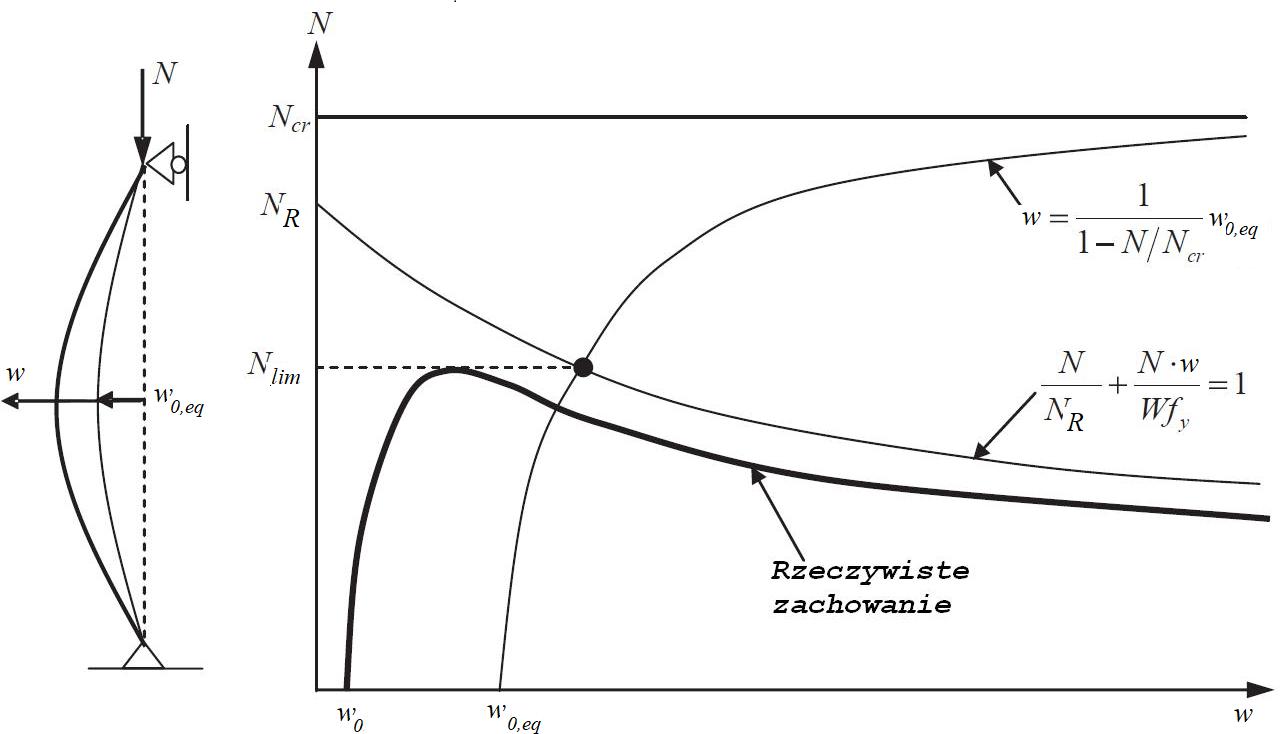
Na rys. 2-3.18 pokazano ilustrację zagadnienia ściskania rzeczywistego pręta w nomenklaturze przyjętej w pracy [zotpressInText item=”{XZT6QNPE}”]. Nośność $N_R$ jest nośnością przekroju na czyste ściskanie. Natomiast $N_{cr}$ jest nośnością pręta (Eulera). Definiuje się następujące mnożniki obciążenia $N$:
krytyczny $\Lambda_{cr}=N_{cr}/N$ (1-1.13),
graniczny (spręzysto-plastyczny) $\Lambda_{lim}=N_{lim}/N$ (1-1.16)
przekroju (nośności plastycznej $N_R=A \cdot f_y$ , $\Lambda_R=N_R/N$
Odróżnienie tego podejścia od prezentowanego w podręczniku polega na tym, że w miejsc mnożnika plastycznego konstrukcji $\Lambda_{pl}$ (1-1.15) stosuje się nośność plastyczną przekroju $\Lambda_R$.W pracy [zotpressInText item=”{52IXD6L3}”] przedstawiono postać formuły Ayrton-Perry (APF) na przypadek zwichrzenia pręta.
Probabilistyczna podejście do stateczności konstrukcji
Już w roku 1950 Dutheil [zotpressInText item=”{XIX2LZYG}”] wskazał na konieczność opisu stateczności słupów w języku probabilistycznym, ale efektywne rozwiązanie problemu probabilistycznego napotykało na przeszkodę związaną z brakiem zamkniętego deterministycznego opisu problemu sprężysto-plastycznej utraty stateczności [zotpressInText item=”{6UG7Z33N}”], a zastosowanie metody Monte-Carlo spotykało się z przeszkodą w postaci małej mocy komputerów.
Jedną z pierwszych prób probabilistycznego opisu problemu stateczności niesprężystego słupa były prace [zotpressInText item=”{22K3HIF3}”], [zotpressInText item=”{QKMMESYF}”] w których jako zmienne losowe traktowano styczny moduł sprężystości, co prowadziło do złożonej, wielokrotnej całki. W pracy [zotpressInText item=”{S6UKF5QS}”] zaproponowano rozwiązanie tej całki aproksymacyjną metodą FORM (First-Order Reliability Method). Podejście sugerowane przez [zotpressInText item=”{XIX2LZYG}”], [zotpressInText item=”{4CA99XPI}”] zastosowano w pracy [zotpressInText item=”{SHWJ3HKH}”] . Przyjęto, że zmiennymi losowymi są wstępne wygięcia (imperfekcje), granica plastyczności i smukłość pręta. Wspólną cechą wspomnianych rozwiązań było założenie o losowej niezależności losowych zmiennych, co jest w ogólności nieprawdziwe.
Szerokie badania problemu prowadził Elishakoff, zarówno metodą Monte-Carlo, jak i metodami analitycznymi [zotpressInText item=”{G6BERSY8}”]. Szeroko stosowaną obecnie ([zotpressInText item=”{JRY8D9IR}”] , [zotpressInText item=”{YNM2GZMC}”] ) metodą modelowania losowych modelowania imperfekcji jest metoda zbiorów rozmytych rozmyte, w której zakłada się, że zarówno kształt jak wielkość imperfekcji, jako przypadkowe.
W analizach losowych imperfekcji najczęściej (np. [zotpressInText item=”{JXA27X6C}”], [zotpressInText item=”{ZBF7QU6I}”] , [zotpressInText item=”{9VQ8RSI9}”] ) tylko amplituda jest uważana za zmienną losową i to o rozkładzie normalnym lub lognormalnym, a jej przebieg na długości pręta przyjmuje się w kształcie sinusoidy. Parametry rozkładu dobiera się tak, by z prawdopodobieństwem 95% imperfekcja pozostawała w przedziale określonym tolerancją normową.
Koncepcja Bj¢rhovde
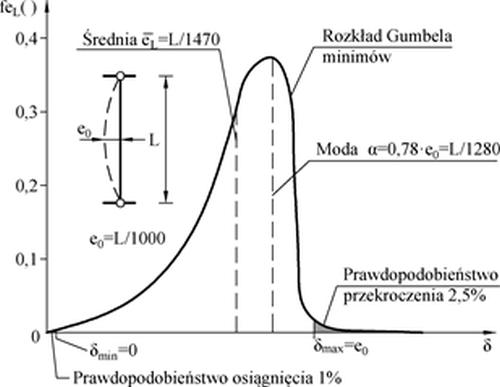
[zotpressInText item=”{E93IL3SI}”] przyjmuje, że losowa amplituda imperfekcji ma rozkład prawdopodobieństwa Gumbela I typu dla najmniejszych wartości (p. Załącznik A). Przyjęty rozkład ma dystrybuantę (A.33) i funkcję gęstości (A.34) ze standaryzowaną zmienną:
$ y=\cfrac{e_0 -\alpha}{\beta}$
gdzie $\alpha$ i $\beta$ są parametrami rokładu, które Bj¢rhovde wyznaczył z warunków brzegowych problemu. Przyjął mianowicie, że maksymalna dopuszczalna strzałka wstępnego wygięcia $e_{max}=e_0=L/1000$ może wystąpić z prawdopodobieństwem 2,5%, co jest zgodne z wytycznymi norm światowych [zotpressInText item=”{RZF2B8R5}”], [zotpressInText item=”{KLU9KLNV}”] i co było zgodne z dawną propozycją europejską. (Obecnie Eurokod przyjmuje $e_0 \approx L/300$.
Z zależności (A.36) dla standaryzowanego rozkładu Gumbela ($\alpha= \beta= 0$) mamy kwantyl $t_{max}=0+1\cdot ln [-ln(0,025)]=1,3$, który jest poziomem tolerancji dla przekroczenia maksymalnej amplitudy imperfekcji $e_{max} = e_0$. Zatem
$$ \begin {equation} e_0=\alpha+1,3 \cdot \beta \label {2-3.57} \end {equation}$$
Ponadto przyjęto, że minimalna strzałka wstępnego wygięcia wynosi $e_{min}=0$ (dla idealnego pręta) oraz założono, że może ona nie być utrzymana z prawdopodobieństwem 1%, co odpowiada współczynnikowi tolerancji $t_{min} =ln [ -ln (1-0,01)]=-4,6 , czyli
$$ \begin {equation} e_{min}=0 =\alpha -4,6 \cdot \beta \label {2-3.58} \end {equation}$$
Z układu równań ($\ref{2-3.57}$) i ($\ref{2-3.58}$) otrzymano:
$\beta=\cfrac{e_0}{5,9}$ , $\alpha= 0,78 \cdot e_0$,
Uzyskany rozkład prawdopodobieństwa pokazano na rys. 2-3.19.
(opracowano na podstawie [zotpressInText item=”{IH3RHUD9}”] )
Na podstawie formuł (A.35) i (A.28) wartość średnia $\overline e_0$ i odchylenie standardowe $\sigma_{e_0}$ amplitudy imperfekcji wynosi:
$$ \begin {equation} \overline e_0 = (0,78-0,5772/5,9) \cdot e_0 = 0,682 \cdot e_0= L/1470 \quad ; \quad \sigma_{e_0}= 1,283 \beta =1,283/5,9 \cdot e_0 = L/4600 \label {2-3.59} \end {equation}$$
Dla parametrów losowej amplitudy imperfekcji {$\ref{2-3.59}$) w pracy [zotpressInText item=”{E93IL3SI}”] sporządzono krzywe wyboczeniowe i porównano z krzywymi deterministycznymi. Oba typy krzywych są podobne, co świadczy o tym, że spośród wielu zmiennych losowych problemu ( w tym naprężeń resztkowych) imperfekcje łukowe są najbardziej znaczące. Metodą probabilistyczną uzyskano większe o kilka procent nośności krytyczne słupów.
Koncepcja Murzewskiego
Murzewski [zotpressInText item=”{KGCMWEBS}”], a za nim Gwóźdź [zotpressInText item=”{5JQLX487}”] przedstawili interesującą, probabilistyczną interpretację współczynnika wyboczeniowego , wyznaczonego na podstawie losowej nośność granicznej $\Lambda_{lim}$ zdefiniowanej jako minimum z losowej nośności krytycznej $\Lambda_{cr}$ (wyboczenia sprężystego) oraz losowej nośności plastycznej $\Lambda_{pl}$ :
$$ \begin {equation} \min {[ \Lambda_{cr} \quad , \Lambda_{pl}]} \label {2-3.60} \end {equation}$$
Osiowe zginanie niesprężystych konstrukcji
Zakres ważności teorii Eulera i Perry-Robertson
W 1845 roku belgijski inżynier [2] pokazał, że teoria Eulera wyboczenia prętów dotyczy przypadków, które dość rzadko występują w praktyce. Słupy rzeczywiste mają smukłość mniejszą od 100, a dla nich wzór Eulera zawodzi (Rys. 2-3.8) i wobec tego Lamarle zaproponował po prostu, aby krytyczne naprężenie rzeczywistych prętów przyjmować równe granicy plastyczności .
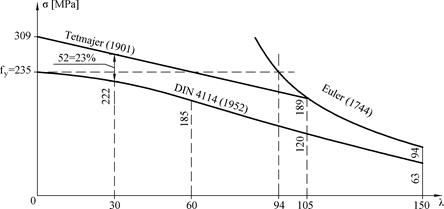
W ślad za pracą Lamarle, teoria Eulera była badana doświadczalnie przez J. Bauschingera i L. von Tetmajera. Bauschinger [3] przeprowadził pierwsze wiarygodne testy na słupach. Tetmajer [4] przeprowadził badania stateczności prętów o różnych przekrojach. Bardziej wszechstronny materiał został opracowany w pracy [zotpressInText item=”{9GXK5HT8}”] oraz [4], którzy zaproponowali empiryczny wzór liniowy do obliczenia naprężeń krytycznych. Na Rys. 2-3.7 pokazano prostą Tetmajera oraz zalecenia normowe DIN z 1952 roku.
(opracowano na podstawie [zotpressInText item=”{W9IB2VFW}”])
Punkt przecięcia krzywej Eulera z wytrzymałością materiału $f_ty$ ma współrzędną $\lambda_{lim}=\pi \aqrt{\tfrac{E}{f_y}} i przykładowo dla stali S355 (E=210 GPa, fy=355 MPa) wynosi$\lambda_{lim}=76,4.
Hipotezy przejścia z krzywej Eulera w prostą fy
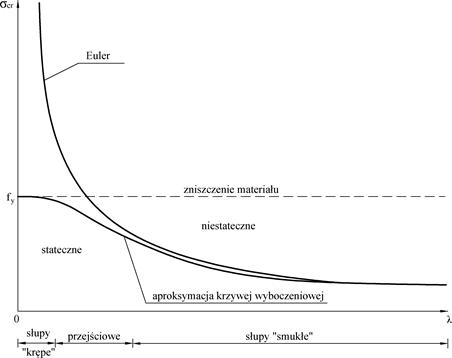
W rzeczywistości przejście z krzywej Eulera na prostą fy nie jest ostre i w obszarze „przejściowym” jest aproksymowane arbitralnie przyjętą, gładką krzywą pokazaną na Rys. 2-3.8.
(opracowano na podstawie [zotpressInText item=”{5MGP6XT3}”])
Sprężysto-plastyczne zginanie osiowe
Klasyczne koncepcje Engesser-Karman
Do opisu sprężysto-plastycznego mimośrodowego ściskania pręta (zginania osiowego) [zotpressInText item=”{VJF5S3PW}”] zaproponował metodę modułu stycznego, polegającą na zamianie w formułach Eulera moduł Younga przez moduł styczny $E_*=\cxfrac{e \sigma}{ e \varepsilon}, przy czym pierwotna propozycja dotyczyła dla całego przekroju.
W dalszych pracach wskazano na błędne założenie, że moduł styczny dotyczy całego przekroju. Faktycznie część przekroju odciąża się i tam powinno być zachowane klasyczne prawo Hooka i zasada płaskich przekrojów (Rys. 2-3.9). [zotpressInText item=”{EA9JGWHV}”] w miejsce $E_*$ wprowadził moduł zastępczy (zredukowany) $E_{**}= \nu E(1+\nu)$, gdzie $\nu$ – współczynnik modułu zastępczego.
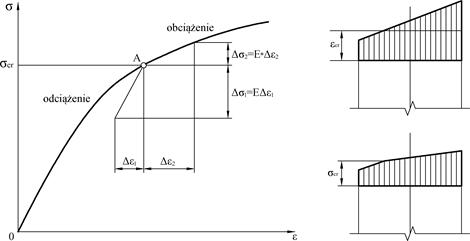
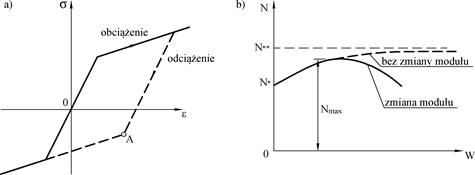
Rys. 2-3.9. Zmiana odkształceń i naprężeń wg Engessera: a) wykres σ-ε, b) zmiana odkształceń, c) zmiana naprężeń
(opracowano na podstawie [zotpressInText item=”{R5U2NNFG}”])
Hipoteza Rankine-Merchant
Prostą formułę na krzywą „przejściową” podali Rankine i Merchant [zotpressInText item=”{EUCB6WQ7}”]. Na podstawie badań eksperymentalnych, stwierdzili, że dobrą zgodność uzyskuje się przy przyjęciu interakcji:
$$ \begin {equation} \cfrac{1}{ \sigma_{cr}}= \cfrac {1} {f_y} + \cfrac {1} { \sigma_E} \label {2-3.2a6} \end {equation}$$
Próby teoretycznego i eksperymentalnego rozwiązania problemu stateczności prętów ściskanych są nadal kontynuowane, a zasady wprowadzone do norm projektowania nie są jedyne.
Koncepcja Shanley
Współczesne koncepcje wyboczenia słupów pojawiły się wraz z opublikowaniem prac [zotpressInText item=”{ZZG3FB75}”],[zotpressInText item=”{IH3RHUD9}”], który wskazał, że przy wyprowadzeniu teorii zastępczego modułu Engessera-Karmana dokonano założeń, które nie mogą być utrzymane. W szczególności nie jest słuszne założenie, że słup pozostaje prosty podczas zwiększania siły osiowej aż do wartości siły krytycznej – dopiero po przekroczeniu, której słup wygina się. Uwzględnienie wyginania słupa od początku procesu prowadzi do mniejszych i bardziej realistycznych obciążeń krytycznych niż wynikające z klasycznej teorii modułu stycznego lub zastępczego.
(opracowano na podstawie [zotpressInText item=”{R5U2NNFG}”])
Na Rys. 2-3.10 pokazano analizę ścieżki równowagi pręta ściskanego siłą N, wykonanego ze sprężysto-plastycznego materiału o biliniowej charakterystyce; w jest bocznym przemieszczeniem sprawczym. Siła wynika z teorii zastępczego modułu (Engessera-Karmana) i jest asymptotą obciążenia krytycznego pręta. Siła odpowiada sile krytycznej wg teorii modułu stycznego Engessera. Na skutek zmiany modułu sprężystości w punktach przekroju podczas zmiany dociążania na odciążenie (pkt A na Rys. 2-3.10a) uzyskujemy siłę krytyczną Shanleya ( punkty na linii ciągłej Rys. 2-3.10 i Rys. 2-3.11). Siłą krytyczną pręta ściskanego osiowo nie jest ani siła , ani , dlatego, że po osiągnięciu przez obciążenie siły Engessera następuje wychylenie pręta ze stanu prostoliniowego i jest to stan stateczny, który utrzymuje się przy dalszym zwiększaniu obciążenia, a zwiększanie obciążenia prowadzi do zwiększania przemieszczenia.
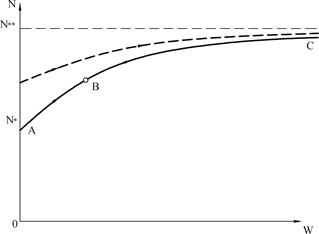
Rys. 2-3.11. Ścieżki równowagi prostego wspornika ściskanego osiowo: – najmniejsza siła, przy której możliwe jest stan równowagi wygiętego pręta
(opracowano na podstawie [zotpressInText item=”{R5U2NNFG}”] )
Koncepcja Shanleya [zotpressInText item=”{IH3RHUD9}”] dobrze koresponduje z niezależnie ogłoszoną teorią, w której pokazano, że przyczyna szeregu niepowodzeń konstrukcyjnych oraz wielokrotnie stwierdzanych „błędów” eksperymentalnych tkwi w niedocenianiu wagi problematyki stanów pokrytycznych, to znaczy utrzymywania się statecznej ścieżki równowagi), po przekroczeniu pewnego poziomu obciążeń, który nie wyczerpuje jeszcze nośności pręta.
Teoria Shanleya pokazuje, że nie można mówić o ścisłej wartości siły krytycznej (granicznej). W zależności od okoliczności można przyjąć za siłę krytyczną obciążenie z przedziału , ale . Wskazuje również, że w problemie stateczności należy mówić o „ścieżce równowagi słupa” i zakończyć pytania o utratę stateczności i siłę krytyczną, nawet w przypadku pręta prostego, osiowo ściskanego!
Wagę koncepcji Shanleya dobrze widać w zadaniu mimośrodowego ściskania, które prowadzi do rozwiązań, schematycznie przedstawionych na Rys. 2-3.12 i z których wynikają następujące wnioski:
-
Literatura
- Ayrton W. E., & Perry J. (1886), On Struts, The Engineer, 464–513
- Lamarle E. (1845), Memoire sur la flexion du l.elsticite des corps, Ann Trwav, 3, pp. 1-64
- Bauschinger J. (1887), Zerknickungs-Versuche (Mitteilung an Das Heft 15, Mitteilung XVII; p. 11). Mechanische-Technologie Laboratorium, Munchen
- Tetmajer L. von. (1890), Die Gesetze der Knickungs und der Zusammeng-Esetzten Druckfestigkeit der Technisch Wichtigsten Baustoffe (Mitteilung Der Material Anstalt Auf Schweizer Polytechnikum in Zurich Heft k, 1890, Heft 8, I896.). Polytechnikum in Zurich
________________________________